多元联系数集对分析的中小机场空管安全保障能力评估

刘本勇

（民航西南空管局 四川省成都市 610202）

目前，许多专家学者在空管安全保障能力定量评估方面进行了探索。付新伟等人采用GRA‐TOPSIS 法建立评估模型，得到空管运行单位安全保障能力的定量结果[1]；李建光通过因子分析法建立中小机场空管安全水平定量评估模型[2]；陈肯等人将集对分析引入中小机场运行风险评估中，预测风险指标的发展态势[3]。本文利用集对分析建立中小机场空管安全保障能力评估模型，将评估系统中的确定与不确定因素作为一个整体进行处理，根据该模型计算出的集对势结果对空管安全保障能力高低进行评判，并通过计算各偏阶联系数对发展动态趋势进行预测，实现定量评估和动态趋势发展预测的有效结合。

1 多元联系数集对分析

1.1 集对分析与联系数

集对分析将系统内两个集合的确定性与不确定性之间的相互作用进行系统性数学分析，从同、异、反三个方面研究集合的不确定性，同时通过联系度描述不确定性。

给定2 个有关联的集合X 和Y，均拥有N 项特征，这2 个集合组成的集对为H=(X,Y)，把集合X 和Y 的特征看作一个系统进行处理，分析集对中X 和Y 的同一性、差异性和对立性。设集合X 和Y 有S 个共同特征，P 个相对立特征，F 个既不共有也不对立的特征，F=N‐S‐P。若令：a= S/N，b= F/N，c=P/N，则该集对的联系度（三元联系数）可表示为[6]：

式中：μ 为两个集合的联系度，a 为两个集合的同一度，b 为两个集合的差异度，c 为两个集合的对立度，a，b，c 属于[0,1]，且 a+b+c=1；i 为两个集合差异度的系数，i∈[‐1,1]；j 为对立度系数，j=‐1。

1.2 五元联系数与集对势

在实际应用中，常将三元联系数中的bi 项进行剖析拓展至多元联系数，一般形式为：

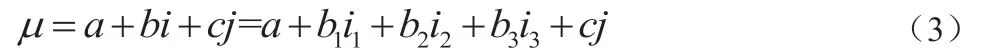
该式称为五元联系数，通常写作为：a+bi+cj+dk+el，其中a,b,c,d,e∈[0,1]，j∈[0,0]为中性标记，不作j=0 解，k∈[‐1,0]，l=‐1，a,b,c,d,e 具有层次性，且读作“正于”，且a+b+c+d+e=1[3]。实际应用中，把五元联系数与安全保障能力的级别对应起来，用a 刻划安全保障能力“高”，b 刻划安全保障能力“较高”，c 刻划安全保障能力“中等”，d 刻划安全保障能力“偏低”，e 刻划安全保障能力“低”。

1.3 五元联系数的偏联系数

多元联系数的偏联系数表示了其同异反确定不确定联系状态的发展趋势。其中，五元联系数的各阶偏联系数分别为：

一阶偏联系数：

二阶偏联系数：

Risk evaluation of geological hazards in Yiliang small grass dam tourist attractions CHEN Tian-he WANG Rong LIU Yi-ying et al.(23)

三阶偏联系数：

四阶偏联系数：

2 基于多元联系数集对分析的空管安全保障能力评估模型

2.1 建立空管安全保障能力评估指标体系

本文借鉴了专家学者的研究成果，同时结合民航空管安全管理的相关规定，建立了中小机场空管安全保障能力评估指标体系[8]。如表1所示。

表1：空管安全保障能力评估指标体系

2.2 确定各级评估指标权重

由于空管安全保障系统的各指标因素相互依存、相互作用，具有一定的复杂性、随机性和模糊性，本文采用不确定层次分析法（AHP）进行指标权重的确定。

假设某一级指标体系中有n 个二级指标，专家采用1～9 比例标度法对二级指标之间的相互重要度进行两两比较，形成区间数及判断矩阵A：

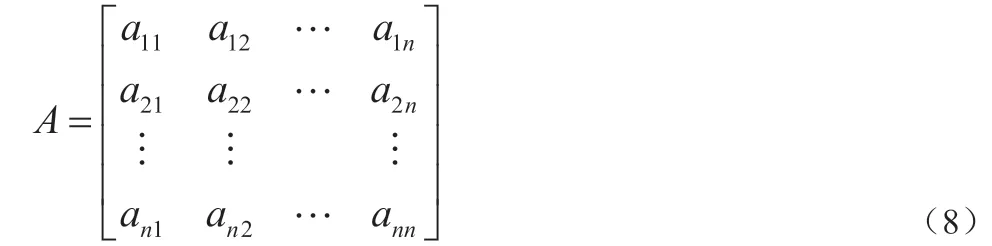
aij表示指标Ai相对于指标Aj的重要程度

根据判断矩阵A，求出矩阵每一行元素的乘积后，对其进行归一化和标准化处理，可得出各评价指标的指标权重。计算公式如下所示：

式中：i 为矩阵阶数；ωi为单层次结构下的指标权重值，则评价指标权重向量表示为W=[ω0，ω2，…，ωi，…，ωn]。

2.3 空管安全保障能力的同异反评价模型

对于空管安全保障能力因素集U={u1，u2…，un}，设W=（w1，w2，…，wn）为因素的权重向量矩阵，评价人对因素ui的评价可以按空管安全保障能力“高”，“较高”，“中等”，“较低”，“低”五级评语，利用公式uij=Nij/N（Nij为将评估指标i 归为空管安全保障能力等级j 的专家人数，N 评估专家总数），对各评估指标的空管安全保障能力等级进行评判，同时结合各因素权重，得以下的同异反评价模型：

其中E=（1ijkl）T为系数矩阵，在集对理论的意义下，wrur1是同一测度分量，为确定项，其综合反映了空管安全保障能力属于“高”的程度；是差异测度偏同分量，为不确定项，其综合反映了空管安全保障能力属于“较高”的程度；wrur3j 是差异测度居中分量，为不确定项，其综合反映了空管安全保障能力属于“中等”的程度；为差异测度偏反分量，为不确定项，其综合反映了空管安全保障能力属于“较低”的程度；为对立测度分量，为确定项，其综合反映了空管安全保障能力属于“低”的程度[9]。

2.4 安全保障能力的态势与趋势分析

若以空管安全保障能力“高”为理想参照集，得出空管安全保障能力评价的联系数，shi（实际‐理想）=a/c，记为shi（H）=a/c。根据五元联系数中的a,b,c,d,e 的数值大小关系进行排序，将空管安全保障能力分为同势（shi（H）>1），均势（shi（H）=1），异势（shi（H）<1）。在此基础上计算出五元联系数各偏阶联系数，对安全保障能力的发展趋势进行深入分析。研究结果表明五元联系数态势表由181 种形式组成，基于篇幅，本文未给出完整的态势表，仅给出实例结果。

3 实例分析

本文以L 机场的空管安全保障能力评估项目为实例，对该模型进行验证。

3.1 计算指标权重

邀请空管系统专家采用1‐9 标度法对空管安全保障能力指标之间的相互重要度进行两两比较，并形成判断矩阵，使用层次分析法计算得到各级指标权重。

3.2 评估风险态势以及趋势

根据以上模型，得到空管安全保障能力联系数计算结果，如下所示：

一级评估指标“运行人员u1”、“运行设备设施u2”、“运行环境u3”和“运行管理u4”以及空管安全保障水平的态势计算结果分别如下：

μ（u1）=0.35+0.44i+0.15j+0.06k+0.00l：a>e，ac，c>d，d>e，同势47 级；

μ（u2）=0.77+0.21i+0.02j+0.00k+0.00l：a>e，a>b，b>c，c>d，d=e，同势2 级；

μ（u3）=0.32+0.28i+0.24j+0.16k+0.00l：a>e，a>b，b>c，c>d，d>e，同势1 级；

μ（u4）=0.50+0.30i+0.14j+0.07k+0.00l：a>e，a>b，b>c，c>d，d>e，同势1 级；

μ（u）=0.49+0.33i+0.13j+0.06k+0.00l：a>e，a>b，b>c，c>d，d>e，同势1 级。

结果显示，L 机场空管安全保障水平的态势处于同势1 级，且属于强同势区，表明L 机场空管安全保障水平等级属于“高”。一级指标中，“运行设备设施u2”、“运行环境u3”和“运行管理u4”分别为同势2 级、同势1 级、同势1 级，均属于强同势区，现状总体状态较好，“运行人员u1”为同势47 级，属于微同势区，表明现状总体状态需引起关注。二级指标中，“空域运行环境状况u31”、“空管应急演练情况u43”分别为均势112 级、均势107 级，均属于弱均势区，表明其状态需加强关注。另外，从L 机场空管安全保障水平总体的变化趋势来看，在一阶层次上呈现下降趋势，在一级指标中“运行人员u1”“运行环境u3”和“运行管理u4”在一阶层次也呈现下降趋势，在二级指标的发展趋势来看，“管制人员配备情况u11”、“空域运行环境状况u31”、“空管应急演练情况u43”、“疲劳程度u44”也需要引起重视。

4 结论

利用集对分析理论对中小机场空管安全保障能力进行评估，不仅可以得到保障能力的量化结果，还可以呈现出整个系统的发展趋势，实现了静态与动态分析的有效结合，为中小机场管理者发现薄弱环节，进行针对性提升提供了科学的参考依据。