用面向对象理念设计线性表的构架

韩海 董蕴源

（江汉大学人工智能学院 湖北省武汉市 430056）

在掌握了一门计算机语言的语法规则和基本技巧之后，学习数据结构与算法是学生提升系统观念和工程能力的关键。学习过程中，多数人比较注重插入、删除、查找等功能函数的编写，不能从总体上把握该章节中各个概念之间的关系[4,5]，因此，梳理各概念之间的关系是非常必要的。

1 线性表各概念间的关系

较有影响力的教材都按照线性表的基本概念、顺序表、链表、栈、队列的次序安排教学内容[1‐3]，先讲述线性表的定义和相关概念，说明线性表的结构特点和应具备的基本功能，包括创建、销毁、判空、提取元素、插入元素、删除元素、查找等等。从规范化的角度考虑，通常都为线性表定义相应的抽象数据类型，描述数据元素之间的逻辑关系，并规定各个功能的函数名称。这是线性表的逻辑结构。然后，分别说明如何按两种常用情况组织数据，在每一种数据组织方式之下如何实现前述功能。如图1所示，线性表、顺序表、链表之间的关系是清晰明确的：用顺序结构组织数据而实现的线性表称为顺序表，用链式结构组织数据而实现的线性表称为链表。

但是，在后续章节讲述栈和队列时就遇到困难。各种教材把栈和队列都定义为操作受限的线性表。因此，栈和队列应该添加到图1 当中。但是，把这些概念都简单地添加到图1 当中作为由线性表直接派生出的形态显然是不合适的，栈、队列是逻辑结构，而顺序表、链表强调物理存储，两者并列会在概念上造成混乱。顺序表、链表、栈和队列都是线性表的具体表现，它们之间的关系如何，目前，还没有任何教材或者文献全面整理了线性表各个形态之间的关系。

图1：顺序表、链表与线性表的关系

各类教材中讲解各种形态的线性表时，除了顺序表、链表、栈和队列之外，还包括环形链表。通常都把环形链表划归链表的一种形态，这更是让学生难于理解：为什么要做成环形？做成环形之后还有表首、表尾吗[6,7]？

2 面向对象理念在线性表中的体现

面向对象程序设计以对象作为基本元素，核心理念包括抽象、封装、继承和多态。抽象是提取事物的属性和行为特征，封装是把属性和行为组织在一起，并规定访问权限，实施这种封装的程序元素是类和实例。继承是通过在已有的类的基础上添加属性、添加行为或者修改已有行为的表现方式而产生新的事物。描述原事物的类称为基类，描述新事物的类称为派生类。多态是指同一种行为在事物中可以有不同的表现形式，在同一个类当中有不同的表现称为函数重载或者方法重载，在基类与派生类之间的不同表现称为函数覆盖或者方法重写。

图1 是一种典型的继承派生关系。线性表是基类，规定了这种结构应具备创建、插入、删除等功能，顺序表是以数组存储数据元素的派生类，链表则是以链式结构存储数据元素的派生类。经典教材都用抽象数据类型规定了线性表的插入、删除操作可以在任何合理的位置进行，顺序表、链表都必须为此编写相应的代码。但是，在用继承派生关系来处理栈和队列时会遇到困难，栈和队列是不允许在任意位置插入、删除元素的，也就是说，栈和队列关于插入和删除操作与线性表有不同的规定，栈和队列在线性表的基础上减少了功能，那么，栈和队列还是线性表吗？目前，各类教材、文献中都明确指出栈和队列是特殊的线性表，却没有解释如何在面向对象的编程方式下屏蔽掉线性表规定的那些功能。

3 用面向对象理念对线性表进行顶层设计

为了解决这些问题，可以重新整理线性表的各形态，明确它们之间的关系。线性结构的最根本特征是数据对象之间有一对一的相邻关系，具有这种关系的数据对象形成线性结构。相邻关系分为左相邻关系和右相邻关系。对于线性结构中的任意数据对象z，最多只有唯一数据对象x 与其左相邻，也最多只有唯一数据对象y 与其右相邻。如果x 是z 的左相邻数据对象（简称左邻），则z 是x 的右相邻数据对象（简称右邻）。左相邻关系和右相邻关系都是一对一关系。

在线性结构的基础上添加一些限制可以产生不同的形态，除了表、栈和队列之外，环也是一种常用形态。每一种形态是一种逻辑结构，它们具有若干共同的特征。

每一种逻辑结构又分别可以采用顺序存储方式或者链式存储方式，一般把顺序存储数据对象的表称为顺序表，链式存储数据对象的表称为链表。相应地有顺序栈、链式栈、顺序队列和链式队列等概念。作为线性结构的第四种形态，可以把顺序存储数据对象的环称为顺序环，链式存储的环称为链式环。上述所有概念的关系构成非常明晰的层次关系，如图2所示。

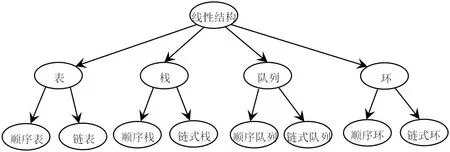
图2：线性结构各种形态之间的关系

记数据对象的类型为ElemType，可以为线性结构定义抽象数据类型如下：

表是规定了方向和两个端点的线性结构。在具备线性结构规定的各项运算的基础上，表新增的运算包括求表长、取指定位置的元素、查找是否存在满足条件的元素、删除元素、排序等，插入和删除操作可以在任何合理的位置上进行。栈、队列和环均是在具备线性结构规定的各项运算的基础上新增若干运算。

很明显，抽象数据类型Linear 缺少了两种重要的运算：删除和查找。这是基于两方面的考虑：一是由创建和插入两种运算就可以搭建出一个线性结构，这两种运算是最根本的运算；二是线性结构的不同形态在删除、查找方面的要求并不一致，作为更高一层的抽象无法描述，只能在表、栈、队列、环等形态中分别规定自己的删除、查找运算及相应的参数形式。

图2 描述的各种线性结构及相互关系与面向对象理念中的继承是直接对应的。针对最顶层的线性结构可以编写一个抽象类，这是其它所有类的基类。第二层的各个概念分别是在线性结构之上添加了若干功能，并且只规定功能和相应参数而不规定如何实现，它们是线性结构的派生类，仍然是抽象类。第三层确定了数据的存储方式，编写的类不再是抽象类，需要为抽象类中规定的各项功能编写函数代码。

例如，位于第二层的环仍然是一个抽象类，对应的抽象数据类型可以描述为：

通常，环是有方向的，在实际设计时做出相应的规定。比如，对于旋转运算Rotate(n)，可以规定在n>0 时把插入、删除操作位置往右邻方向移动，n<0 则向左邻移动。添加新元素有多种做法，涉及把新元素添加为当前位置的左邻还是右邻，以及当前操作位置是否移动。可以在上述抽象数据类型中以说明的形式加以规定，也可以把这些细节留给派生类。

在确定了用数组或者链表作为数据对象的存储方式之后，对图2 当中第三层的顺序环或者链式环可以编写相应的类，并在这种存储方式之下实现创建、消除、插入、删除、查找、旋转等功能。

在线性结构中添加环这种形态之后，就可以顺理成章地解释为什么需要有环形链表、双向环形链表等形态。环的应用则有著名的约瑟夫问题：n 个人排列成圆形，每个人用编号表示，第1 个人从1 开始报数，报到m 的人退出，下一个人重新从1 开始报数，如此反复。对于给定的正整数n 和m，求退出的次序。在编写了图2 第三层的顺序环类或者链式环类之后，利用环这种形态及动态联编技术，可以很简洁地实现约瑟夫问题。用C++语言编写的核心代码如下：

除此之外，检索技术中的线性探查法是环的一个重要应用。用散列表组织数据时，线性探查法是最常用的冲突处理方法，该方法把数组视为一个首尾相接的环，第0 号下标与第n‐1 号下标是相邻元素，当存储新元素发现有冲突时，按环的形态进行旋转逐个查找下一位置，直至找到合适位置把新元素存入其中。

4 结语

线性结构是最重要的逻辑结构，除了表、栈和队列之外，线性结构还应包含环作为第四种形态，每一种逻辑结构又分别可以有两种不同的数据存储方式。按图2 表述线性结构的各种形态，使得各种形态及具体实现之间的关系清晰明了，也与自上而下的设计理念相对应。按这种方式组织相关知识的教学，不仅让学生掌握各个具体的知识点，更能让学生站在更高的角度观察问题，把握知识的总体构架。