应急物流保障约束下的选址与资源配置研究

陈 亮

（黄山学院 数学与统计学院，安徽 黄山245041）

1 前言

我国是一个自然灾害高频发生的国家，历次的地震、洪水、台风等自然灾害给我国的经济建设和人民的财产安全带来了严重影响。而我国每年花费在应对这些灾害所造成的物流成本特别高。应急物流建设的成败直接关系到人民生命财产安全，关系到社会的长治久安。从战略层角度说，它与国家、政府、人民群众的利益密不可分；从战术层的角度来说，它又关系着百姓的安居乐业。所以应该结合战略层和战术层考虑，层层搞好应急物流建设，保障国家稳定发展，人民生活安康[1]。

本文结合自然灾害和救灾物流的特点，定量化地研究了正常条件下救灾资源储备库的选址和物资配置，模型加入了一个惩罚系数，因此模型含有一定的鲁棒性[2]。通过对模型进行扩展，对约束条件提出更加严格的保障，建立了一个具有服务质量保障约束的储备库选址和资源配置的模型，并对参数进行灵敏度分析，并结合实例做出研究，解释了加入的约束条件对模型的影响，对考虑实际问题做出了一些启示[3]。

通过对选址与配置模型作简要的研究，可事先在不确定环境的情形下做出最佳决策，在相应的节点存放一定数目的物资来应对各种不同的可能发生的自然灾害。目标则是一种权衡，在储存费用和惩罚费用之间做出决策，而有些灾害发生概率较低，破坏程度高，一旦发生可能事先存放的物资均遭到毁坏，不仅浪费了资源，增加了额外的储存费用，也可能由于物资的毁坏而带来未满足需求，增加了惩罚费用，若将所有情景下所有物资需求均考虑到，最大程度上的减少惩罚费用，问题将变成只有过分储存费用而没有惩罚，这无疑增加了问题难度也缺乏实际意义。因此最小化成本模型舍弃一些发生概率低同时破坏程度极高的自然灾害，考虑那些可控性高的情景模型，即做出的努力就可降低模型的成本[4]。本文提出了一个带有服务质量保障约束的资源选址与配置模型，在不确定性的环境下服务质量保障约束是从物资的数量和运送的距离两个方面考虑的，首先提供一个可信度水平α，即一些情景的发生概率和，在可信度水平下情景需求均得到满足，在道路网络中提供充足的物资，保障了物资的数量；然后限制每种物资在整个救灾过程中运送总距离，这比数量保障在灾害的应急响应上更加严格[5]。

2 带有服务质量保障约束的选址与资源配置模型

2.1 问题描述

在本模型中，我们加入情景模型。对不同情景进行定义区分，设置可靠集合，每个情景都可能被选入到可靠集合内，可靠集合内部的情景需求必须得到满足，且物资运送距离也有一定的限制，可靠集合之外的情景运送距离不受限制，且物资需求未满足时要接受惩罚。同时库存的容量的道路的流量是受到一定限制，物资的获取主要通过事先储备库的调配，暂不考虑其他途径。因为不同情景下的需求不同，不能确定所有需求均得到满足，为此增加未满足需求的惩罚函数，在一定程度上提高了模型的鲁棒性[6]。

2.2 数学模型

考虑库存因素未涉及具体车辆路线，结合参数α和Dk（单位物资运送距离）的设置以及仓库类型对最优解的影响，考虑了事先存放物资的完好性和道路的毁坏性，在不同情景下需求情况和道路状况是不同的，通过离散化情景对不确定性构建[7]。

集合：

A为弧的集合，∀(i,j)∈A；

S为情景集合，s∈S；

N为所有节点的集合，I为所有需求点集合，即所有候选节点，i∈I；

K为物资种类集合，k∈K，L为仓库集合，l∈L。

参数：

Fil为在需求点i建库存l的固定费用，不同类型的固定费用不同；

bk为单位物资k的容量；

Ml为库存l的最大容量；

qk为单位物资k的储存费用；

hk单位物资k未使用的额外储存费用；

Dk单位物资k的运送距离上限；

pk为单位物资k的惩罚费用，一般比物资的购买价格和储存费用高出多倍；

dij为从i到j的距离；

为情景s下灾后道路i到j容量上限；

Ps为情景s发生的概率，；

u为一个无穷大数

决策变量：

yil为0-1变量，表示是否在需求点i建立类型为l的库存；

为情景s下i点存放物资k的未使用量；

为情景s下的i点物资k未满足量，由于仓库事先存放的不足；

γs为0-1变量，表示情景s是否被选入到可靠集合中。

数学模型：

模型是一个两阶段的随机混合整数规划问题，yil和rk i为第一阶段变量，在未知任何具体的灾难情景前做出的；、γs第二阶段变量，都依赖于情景变化的，也称资源变量。通常在问题规模不是很大的情况下，可以将模型进行扩展变形转化为确定性等价列的方法进行求解，简化问题的难度[8]。

式（4.1）表示两阶段总费用的最小和，其中有第一阶段事先选址时所有需求点的建立、所有类型仓库固定费用和物资的储存费用，该阶段发生在灾害前，与情境无关，第二阶段的费用为所有节点之间物资的运输费用、资源未使用部分的额外存储费用以及需求点所需物资未得到满足的惩罚费用，该阶段发生在灾害后，决策变量与情景有关。式（4.2）是流量平衡约束，在所有情景下每个节点的每种物资进入量都应等于进出量，是灾难发生后可以使用未遭到破坏的物资数量，其中和分别为未使用量和未满足量，二者不能同时存在。式（4.3）为库存容量限制约束，即事先在所有节点存放的物资的容量总和必定不能超过该点设置仓库的容量。式（4.4）为仓库类型的约束，即在某点设置仓库时只能选择一种仓库类型。式（4.5）限制了每种物资从出发点到受灾点的运送距离，可靠集合内的情景下的运送均要受到限制，u是一个相当大的数，因此可靠集合外的情景不做运输距离的要求。式（4.6）为道路流量上限约束，考虑到灾害可能会对道路的通行能力造成影响，每条道路上的所有物资的运输流量都应受到限制。式（4.7）定义了可靠集合，集合内的所有情景发生概率和不得小于α。式（4.8）确保了可靠集合内的所有情景下的物资需求均得到满足。式（4.9）、（4.10）为第一阶段决策变量的取值约束。式（4.11）、（4.12）、（4.13）为第二阶段决策变量取值约束。式（4.5）、（4.7）、（4.8）约束为服务质量保障约束，从物资的数量和距离两个方面保障了服务的质量，提高了模型的服务能力与水平，也便于在设置不同参数条件下更好地对模型进行分析，更具有理论特色和实际意义[9，10]。

3 模型求解和算例分析

3.1 算例描述

为了简化问题的规模和更好地分析服务质量保障约束对选址与配置最优解特征的影响，考虑5个节点6段道路连接的网络，具体的节点位置如图1所示，图上的数字代表距离，也被用于运输费用，道路上的运输费用在表1中说明，假设没有道路连接遭到毁坏，运输网络仍然是紧密连接的，所以道路的通行是没有流量限制，为了简化假设物资在每段道路上的运输费用是一样的，同时只考虑一种可以事先储备充分的物资，表2给出了3种情景下需求点的位置和需求量。每种仓库的固定费用和容量大小由表3提供，同时考虑3种不同情景下的救援工作，每种情景发生的概率是已知的，而且概率和为1。每种情景都有可能对网络道路的流量和事先存放的物资有一定的影响，进而产生大量需求。费用单位为元，容量单位和需求量单位为吨。

图1 简单网络结构情况

表1 道路运输费用情况()

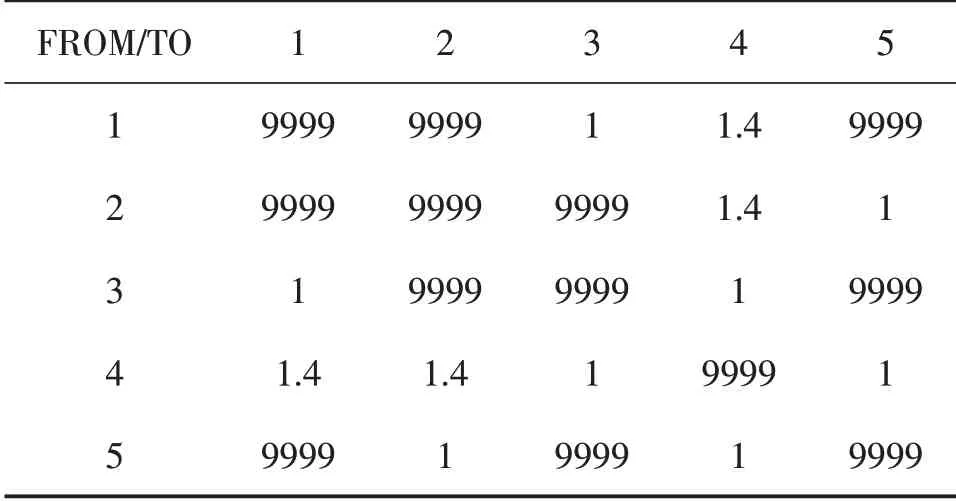
表1 道路运输费用情况()

FROM/TO 1 2 3 4 5 1 9999 9999 1 1.4 9999 2 9999 9999 9999 1.4 1 3 1 9999 9999 1 9999 4 1.4 1.4 1 9999 1 5 9999 1 9999 1 9999

表2 情景下物资需求量()

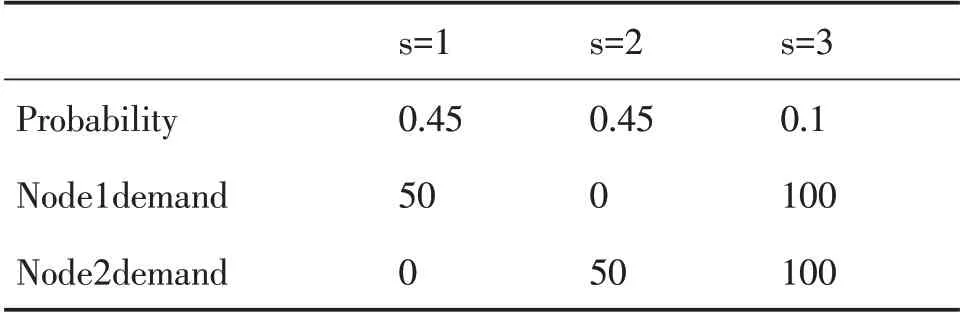
表2 情景下物资需求量()

Probability Node1demand Node2demand s=1 0.45 50 0 s=2 0.45 0 50 s=3 0.1 100 100

表3 仓库固定建设费用和容量大小

3种情景下的情况：第一种情景发生概率为0.45，p()1=0.45，节点1有需求，而且事先存放在1的物资有一半遭到毁坏；第二种情景p()2=0.45，与情景1下相同的情况发生在情景2下的节点2；第三种情景下事先存放在1和2的物资得到毁坏，节点1和2对物资都有较多的需求，p()3=0.1。因此我们尽量选址建在更安全的地方如节点3、节点4或者节点5，可以分析出小型库存即可满足情景1和情2的需求量，但是一旦情景3发生就没有一种仓库可以满足，只能建立多个仓库了。假设物资的单位购买价格是5，单位容量为1，物资未得到满足的单位惩罚费用是购买价格的10倍，而物资存储过量的单位储存费用为购买价格的1/2，我们尽量使得物资得到满足，目标函数是在物资的储存费用、运输费用和惩罚费用中的权衡，总和最小。

3.2 模型求解

该实例第一阶段共有15个变量，第二阶段有48个变量，通过线性规划求解器可以进行求解，方法是将救灾中的不确定性通过情景的构建转为确定性问题求解，需求是通过实例数据和应急系统预测得到，并对道路和网络状况做出假设，真实的数据具有一定的参考意义，也便于我们后续分析。

当没有服务质量保障约束时即没有约束条件（5）、（7）、（8）时，问题的最优解是在节点4建立一个容量为100的小仓库，并且存满物资。从最优结果上看，选址似乎变得很敏感，节点4位于网络的最中间，也在节点1和节点2之间，到两点的距离和是最近的，不确定节点1和节点2是否有需求，所以选在保守的节点4储备物资。目标函数依然是对各个部分费用的折衷权衡，包括建厂的固定费用，物资储存费用，物资运输费用以及可能发生的惩罚和过度储存成本，在节点4建立小库存满足了情景1和情景2下物资需求，但当情景3发生时，节点1和2均需求100单位物资，超过了事先在节点4小库存的容量，所以不得不考虑在该情景下是选择不满足需求带来的惩罚还是尽量满足需求带来的额外费用。考虑到情景3的发生概率只有0.1，而在该情景下未达到物资满足所接受的惩罚费用要低于选择更大容量的仓库的固定费用和储存成本，所以我们将舍弃对情景3的需求研究，接受惩罚。目标费用最优值是1339.5，而在节点4选择大库存费用为1409。选择大库存导致额外支付的固定成本和储存费用要大于惩罚。

尽管小仓库的容量只有100，但将物资存满达到容量上限是值得的，即使在情景1和情景2的概率和为0.9的情况下会有物资的未使用而过多承担储存费用，这些费用也小于在情景3的发生概率为0.1的情况下带来的物资惩罚费用，这种做法是可行的。

具体情景下物资调运情况：用[]±来代表物资的需求和供应情况，“+”表示需求，“—”表示供应。

S=1时，

节点1：v1[-50]+r1[0]+x41[50]=[0]

节点2：v2[0]+r2[0]=[0]

节点3：v3[0]+r3[0]=[0]

节点4：v4[0]+r4[100]+x41[-50]=[50]

节点5：v5[0]+r5[0]=[0]

情景1下所有节点的所有物资均得到满足，同时由于存储数量大于需求量，产生了未使用的物资的储存费用，运输费用为50×1.4=70，物资存储费用为50×2.5=125，第二阶段总费用为0.45×(70+125)=87.75。

S=2时,

节点1：v1[0]+r1[0]=[0]

节点2：v2[-50]+r2[0]+x42[50]=[0]

节点3：v3[0]+r3[0]=[0]

节点4：v4[0]+r4[100]+x42[-50]=[50]

节点5：v5[0]+r5[0]=[0]

情景2下和情景1大致相同，只是需求点从1变到了2，有50单位物资未使用，运输费用为50×1.4=70，未使用物资存储费用为50×2.5=125，第二阶段总费用为0.45×(70+125)=87.75。

S=3时,

节点1：v1[-100]+r1[0]+x41[50]=[-50]

节点2：v2[-100]+r2[0]+x42[50]=[-50]

节点3：v3[0]+r3[0]=[0]

节点4：v4[0]+r4[100]+x42[-50]+x41[-50]=[0]

节点5：v5[0]+r5[0]=[0]

情景3下存在为满足需求，1和2的需求大于4点存放物资的数量，且事先存放在1和2的物资全部被毁坏，需要接受惩罚，惩罚费用为100×50=5000，运输费用为100×1.4=140，第二阶段总费用为0.1×( )140+5000=514，所以在4节点存放100单位物资的最优决策目标值为650+87.75+87.75+514=1339.5。

最优解在节点4建立小库存存放100单位物资是可以满足情景1和情景2下物资的需求，但无法满足情景3下节点1和节点2的需求，所以本模型的可信度水平为情景1和情景2的发生概率和，即为0.9,该模型能够在此概率上满足需求保障服务数量来达到最优；单位物资运送距离由网络图中显示，最大距离不超过1.4，即为单位物资平均运送距离上限。

3.3 灵敏度分析

根据上个实例的结果分析，服务质量保障的两个参数α=0.9，Dk=1.4，我们把这二者加入到模型中作考虑，当α≤0.9，Dk>1.4时，对模型的最优解没有影响，但若对服务质量保障提出更高的要求，要求物资的数量更为充足以防惩罚的出现，或者对物资运送距离提出更短的限制，那么在节点4建立小库存且存放100单位物资的最优解将不再适应了。当α>0.9时，则要求满足所有情景下的物资需求，本实例中情景3的发生概率为0.1，若低于0.1，还存在其他情景，那么当α>0.9时就不用考虑所有情景。若必须改变传统的解，可以选择建立大库存或者在更多的节点存放物资来保障物资充分供应，如果建立两个存储中心的话，节点3和节点5不失为很好的选择，最优解将变为在这两个节点建立容量为100的小库存，总容量满足所有情景下的物资需求，即使在最坏的情景3下也能满足需求，此情况下的最优目标值为1420，相比原来没有加入服务质量保障约束时提高了6%，可以将提高的6%看成更高要求的服务质量的边际价格。

如果对单位物资运送距离提出更高的约束，Dk<1.4时，传统的解也同样不再符合，为了保障运输距离更近不得不增加存储中心的数量，最优解也由在节点4建立库存变为分别在节点3和节点5都建立库存，两个存储中心运送到各个潜在的需求点的距离就变得更近了。

当然α和Dk的变化不一定会带来相同的最优解的变化。在模型中储存仓库的类型分为多种，可从库存容量出发，将大型库存容量由150变为200。α的提高可能要求增加物资储备，但储备量受到库存容量的限制，或者增加储备仓库的数量，而Dk的降低一般要求增加存储仓库的数目来保障距离约束了，库存容量的大小影响着这两个参数变化带来的不同结果，通过求解可以看到：（1）当没有加入服务质量保障约束时，大仓库容量的变化没有对解的情况产生影响，因为即使选择新的仓库在节点4建立大库存，其潜在降低的惩罚费用没有超过可能带来的储存费用，权衡后的解依然不变；（2）当服务质量保障约束加入到模型中，α>0.9时最优解则变为在节点4建立容量为200的库存并填满库存，为满足所有情景下的需求，特别是最坏情景3下的200单位物资，而大库存正好符合。Dk<1.4时最优解不受影响，仍然是在节点3和节点5建立两个小库存，因为大仓库的容量提高对运输距离没有影响，即使要换成新的仓库仍然要在至少两个点建立存储仓库才能保障运送距离，不仅费用会大幅度提高，也没有使运送距离有所保障。

将α和Dk两个参数的变化对解的结构的影响总结在表4和表5中。

表4 大库存容量150的最优解结构的变化情况

表5 大库存容量200的最优解结构的变化情况

4 结论与展望

模型中的目标函数是一种对各部分费用的折衷权衡。最优解也是在α和Dk的确定下的权衡结果。随着α的提高，模型就要卷入更多的情景考虑，把更多的情景纳入到可靠集合中，保障更大概率的救灾需求，这无疑将增加难度，要求事先存放更多数量的物资，相应的可行措施为选择库存容量大的仓库存满物资，或者选择更多的节点存放物资，这依赖于α和Dk的具体数值。

当单位物资最大运送距离的约束变紧时，则要求在可靠集合内的运输距离变得更近，只能采取提高存储中心的数目这一措施来保障。把α和Dk结合起来，当服务质量保障约束变得更严格时，α变大，Dk变小，这就可能导致选择更多的存储中心、存放更多的物资、更近的运送距离在可靠集合内的情景中。可以将二者分开研究，固定一个参数来研究另一个的变化给解结构带来的影响，当然也可将二者结合起来，目标函数的最优值通常就是将二者结合来优化分析。

本文主要在学者研究的基础上对救灾物资储备库选址与资源配置模型做出延展，提出了服务质量保障约束的概念，并把它加入到模型中，使得模型从救灾物资的数量和物资运送距离两个方面都有了保障，对救灾服务质量有了更为严格的要求。通过一些实例求解分析，得出α和Dk两个参数的变化对最优解结构的影响，以及库存的变化对模型的影响，通过设置可靠集合更加清楚模型能够解决的实际救灾问题，以及增加的服务质量保障约束的边际价格，对实际研究救灾物流有很大的帮助。同时最优解的变化也对应急救援决策者在救灾工作中提供了理论参考，具有较大的实践意义。