某密封件基于公差配合的仿真研究

梅杰，李冠东，黄嘉炜，王宏

（200093 上海市 上海理工大学 机械工程学院）

0 引言

在工程实际应用中，公差的配合及选择至关重要，而合适的公差配合会让结构部件具有更好的工作性能、更高的使用寿命及可靠性[1]，同时还能为企业节省制造成本，提高生产效率，从而带来效益。Jayaprakash G[2]等通过开发参数化计算机辅助设计模型，进行装配部件公差分配，以确保在考虑装配部件尺寸和几何公差的影响下，产品满足功能和质量。此外，还确定了由于惯性和温度效应引起的机械装配各部件的变形，将其与公差设计相结合；并通过电机装配的应用实例，验证了该方法的有效可行性；孙子莹[3]等研究浮动密封不同结构下浮封座间隙对密封性能的影响规律，满足密封性能要求时浮封座间隙匹配，找出浮动密封满足密封性能时端面比压随浮封座间隙变化影响不敏感的结构，理论说明原理并进行了试验验证；郑国运[4]等采用有限差分和有限元相结合的方法，通过建立耦合模型，分析镶嵌式流体动压型机械密封的配合公差对密封性能的影响。通过计算表明，选定的4 种配合公差对机械密封的密封性能影响较小；配合公差对密封性能的影响与镶嵌结构和材料有关；安晓卫[5]等采用有限元法，计算分析装配后密封环上的位移分布情况，研究密封环配合面上尺寸公差和形位公差对装配后密封环密封性能的影响。结果表明，配合面上的尺寸和形位公差，均会引起配合面产生不同程度的变形，从而影响机械密封装置的密封性能；逯世廷[6]以某型号发动机为研究对象，针对连杆轴承和连杆小头之间的过盈配合的过盈量研究其微动现象，对连杆小头组件在发生爆压时，通过有限元仿真研究其接触过程，得到过盈量对连杆轴承微动特性影响规律。而通过查阅文献发现，对于橡胶材料的公差配合的研究较少。

本文研究通过理论计算出浮封圈端面的公差配合，再用仿真来模拟装配过程，这为一种用仿真来验证公差配合适用性的方法提供参考。

1 研究方法

以某支重轮中的浮动密封为对象，重点是浮封腔中的浮封圈，它的过盈量直接影响公差的配合。研究步骤如下：理论计算装配结束后浮封圈端面的最佳过盈量以及选择最佳公差配合；再以不同浮封座间隙下的模型为基础，选用理论计算的过盈量匹配后的公差，进行装配过程的仿真，通过位移云图预测胶圈的变形率。某浮动密封的截面图如图1 所示。

图1 浮动密封结构图Fig.1 Floating seal structure

2 理论计算

通过最小结合压力Pfmin，包容件与被包容件传递负荷所需的最小直径变化量eamin和eimin来计算传递载荷所需的最小有效过盈量δemin。

通过包容件与被包容件不产生塑性变形所容许的最大结合压力Pfamin，Pfimin最大直径变化量eamax，eimax来计算最大有效过盈量δemax。

3 仿真

通过ABAQUS 有限元仿真软件在上述的公差配合下，确定不同浮封座间隙下浮封胶圈的变形以及该间隙下浮封胶圈在浮封腔中的最终停靠位置，通过浮封胶圈在装配结束后的变形和位置验证该公差配合的适用性，参见图2。具体实施步骤如下：

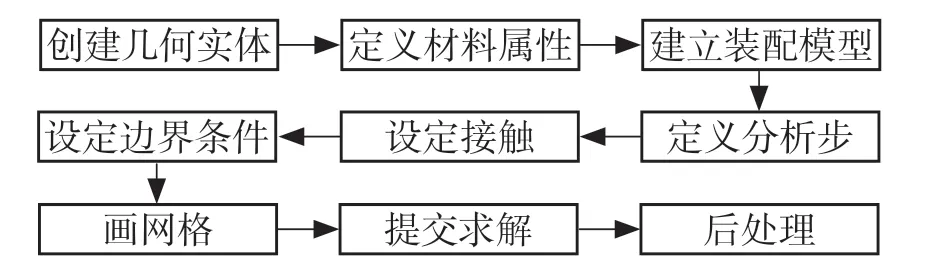
图2 有限元仿真步骤图Fig.2 Finite element simulation steps

（1）建立几何模型

浮封胶圈是该仿真分析主要分析对象，因此在建立几何模型时，选取浮封胶圈、浮封环和浮封座进行建模，按照之前计算的公差配合进行装配，模型如图3 所示。由于浮动密封组件是各个截面一致的环状组件，因此可直接选取环状中的一个截面建模。在建模的过程中，简化了对其他不影响分析结果的区域，例如草图绘制过程中去除了倒角、倒圆等。

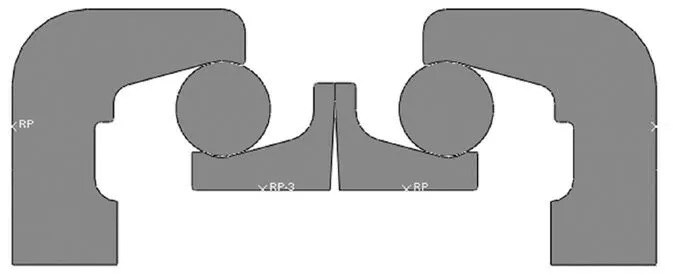
图3 浮动密封几何模型Fig.3 Geometric model of floating seal

（2）定义材料属性

本次分析中的材料属性定义为浮封座和浮封环的金属材料和浮封胶圈的超弹性材料。这种非线性材料通常采用两个参数的Mooney-Rivlin 本构模型，如式（3）所示，可得合理的近似值[7-8]

式中：C01，C02——Mooney 系数；I1——第一应变张量不变量；I2——第二应变张量不变量。

Mooney-Rivlin 模型中只要确定C02/C01的比值，再由弹性模量Ea 与剪切模量G 的关系式就可以得到C01和C02，其关系式如下：

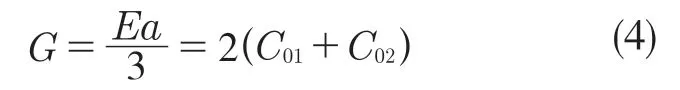
橡胶邵氏硬度HA 与弹性模量Ea 的转化关系式如下：

对材料定义如下：在仿真软件中设置弹性模量为210 GPa，泊松比为0.3，如图4（a）所示；浮封胶圈硬度HA 为60±5，Mooney-Rivlin 模型参数C01=0.84，C02=0.21，如图4（b）所示。

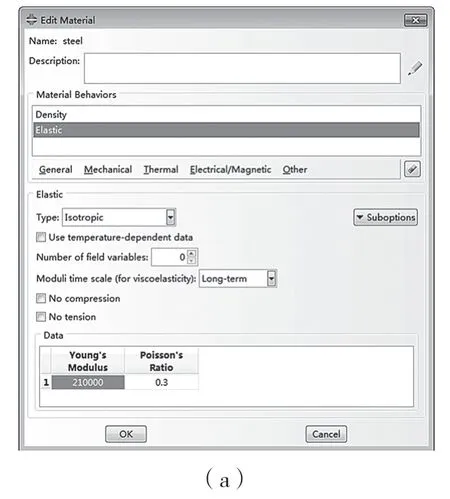
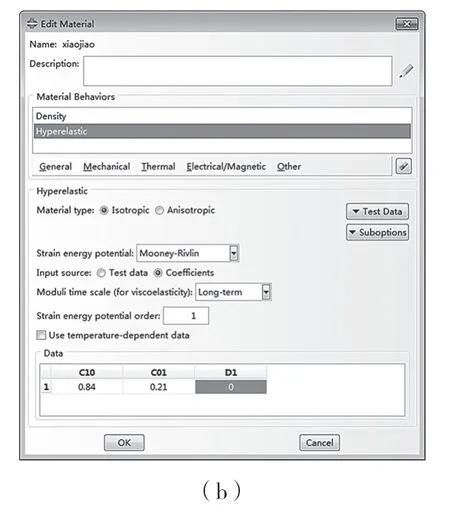
图4 定义材料属性Fig.4 Definition of material properties

（3）施加约束及载荷

浮封胶圈变形后发生自接触，且接触时胶圈的变形较大，因此在该仿真分析中主要定义了浮封胶圈自接触、浮封环与浮封胶圈、浮封座与浮封胶圈3 种接触对，如图5 所示。

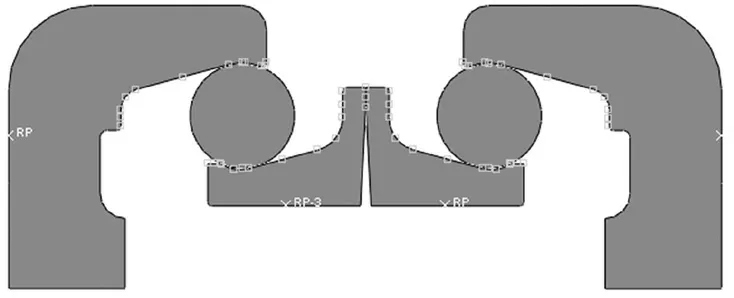
图5 接触对定义Fig.5 Definition of contact pairs

其中，设定边界条件如图6 所示。对浮封座施加固定约束，在平稳建立接触关系后，再施加位移，观察浮封胶圈的位置以及变形情况。

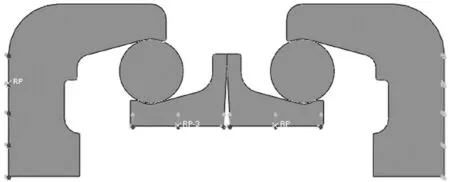
图6 边界条件设定Fig.6 Setting of boundary conditions

（4）有限元模型网格划分

在进行网格划分时，考虑到浮封胶圈的位置和变形，需要设置较小的浮封胶圈网格尺寸和接触的区域位置处的网格尺寸，较大的浮封座和浮封环的网格尺寸，结果如图7 所示。

图7 网格划分Fig.7 Grid division

（5）仿真结果分析

参数定义结束后，求解有限元模型，得到该模型的有限元分析结果。为验证该浮动模型的装配过程，先定义一个浮封座间隙，将浮封座移动至正常工作的装配位置，再求解。有限元计算结束位置如图8 所示。

图8 装配位置Fig.8 Assembly position

然后求解在浮封座间隙较大处取10 mm 时的有限元模型（如图9 所示），浮封胶圈的位移云图（如图10 所示）。

图9 间隙为10 mm 时结束位置Fig.9 End position when the gap is 10 mm

图10 间隙为10 mm 时胶圈位移云图Fig.10 Rubber displacement cloud when the gap is 10 mm

通过分析结束位置和位移云图发现，当浮封座间隙为10 mm 时，浮封胶圈受挤压发生变形，变形后没有碰到浮封环的内侧，而位于浮封环的内锥面上，该间隙下浮封胶圈的变形满足变形率要求且变形的位置合理。

最后，求解浮封座间隙为零时的有限元模型。组件计算结束时的位置如图11 所示，浮封胶圈的位移云图如图12 所示。

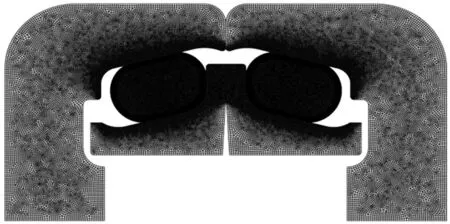
图11 间隙为0 mm 时结束位置Fig.11 End position when the gap is 0 mm

图12 浮封座间隙为0 mm 时浮封胶圈位移云图Fig.12 Rubber displacement cloud when the gap is 0 mm

分析结束位置和浮封胶圈的位移云图可以看出，当浮封座间隙为零时，浮封胶圈的变形会受到浮封环内侧的影响，最终位于靠近浮封环内侧的锥面上，其变形也在合理的变形率范围内。

综上所述，通过分析结束位置和位移云图得出，在这两个间隙下浮封圈的变形率在合理范围内，而且当间隙为0 即最大变形时，其变形率也在合理范围内。

4 结论

本文通过选用不同浮封座间隙下的浮动密封截面模型，对其装配过程进行仿真分析，获得不同间隙下装配结束位置图和浮封胶圈的位移云图，经分析得出以下结论：

（1）浮封座间隙越大时浮封圈的变形越小，浮封座间隙越小时浮封圈的变形越大，其中，最大间隙和最小间隙处浮封圈的变形都在浮封胶圈材料所允许的合理范围内，说明在该公差配合下浮封胶圈在合理的适用范围内，并没有导致浮封圈失效。

（2）浮封胶圈的变形会受到浮封环内侧面的影响，浮封胶圈变形后位于靠近浮封环内侧面的锥面上，但该情况下浮封胶圈变形后与浮封环接触宽度的变化受浮封环侧边的影响微乎其微。

本文提出了如何通过有限元仿真分析来验证公差配合的适用性，验证了该公差配合的合理性，说明通过过盈量来匹配公差这种方法的准确性，证明了该过盈量的计算较准确，该方法计算的过盈量有效，这为公差配合的选择提供了参考。