基于改进面波技术的转换波静校正方法研究

蔡露曦，付兰兰，王 强，张森垚，张 昊

(西安石油大学 地球科学与工程学院，西安 710065)

0 引言

转换波勘探技术能够提供地层岩性信息，可以应用于解决储层识别、裂缝预测以及流体识别等问题[1]。静校正是复杂地区油气地震勘探资料处理中的关键环节[2-4]，其中接收点横波静校正量的求取是转换波静校正处理的重点和难点[5]。由于转换横波的速度通常远小于纵波速度，且不受流体孔隙的影响，其低速带往往延伸至潜水面之下，在表层结构复杂地区，资料中的反射波组混乱[6]，静校正问题十分突出[7-8]。由于在实际勘探中通常使用纵波震源，非转换型的横波不发育，因此常规的基于反射波和折射波的转换波静校正方法在处理中具有一定难度[9]。

利用资料中信噪比较高的面波进行横波静校正量的计算，是一种较有优势的方法。面波具有频散特性，利用频散曲线能够反演建立低速带的横波速度结构[10]，郭良辉[7]和邓帅[11]等发展了基于面波的转换波静校正处理方法。然而常规面波处理技术基于多道面波分析提取频散曲线，存在横向分辨能力较差的缺点[12-13]，处理结果反映的是多道检波点下方的平均速度结构，孟小红等[14]指出该方法得到的是P-SV波横波静校正量的长波长趋势，无法预测横波静校正量的短波长分量。该研究拟对面波静校正技术进行改进，引入波场分离和面波谱分析[15-17]计算各检波点位置处的频散曲线，进而建立各检波点的横波速度结构，获得每个检波点独立的横波静校正量，提高处理的精度。

1 改进面波技术静校正原理

针对P-SV型转换波的横波静校正量计算问题，该研究利用资料中与SV型横波关系密切的瑞雷面波进行处理。瑞雷波的质点在竖直平面内振动，不同频率成分具有不同的传播速度和穿透深度，其各频率的传播速度主要受地下介质的横波速度结构控制[10]。为了提高静校正处理的精度，该研究将面波从资料中分离出来，并重建得到仅含单一模式的面波记录，然后再计算静校正量。设共炮点道集记录为d(x，t)，利用F-K变换法对地震波场进行分离和重建，首先对信号在时间域做傅立叶变换，计算式如下

(1)

(2)

式中:f表示频率；k表示波数。

经过式(1)计算，原始地震信号就由时间域变换到了频率域，然后再利用式(2)将信号变换到波数域，最终得到频率-波数域的信号D(k，f)。在频率-波数域中面波信号会聚集形成明显的能量团。

面波具有多模式发育的特点，该文仅考虑能量较强的基阶模式面波，并对频率-波数域能量谱中的基阶模式面波进行分离，再对分离后的面波能量谱做F-K逆变换，就可以重建仅含基阶模式面波信号的地震记录。然后利用面波谱分析(Spectral Analysis of Surface Wave，SASW)方法对重建的面波信号进行处理，即可获得邻近检波点之间的频散曲线[18]。设某两道信号分别为s1(t)和s2(t)，二者频谱可通过傅立叶变换得到，计算如下:

(3)

(4)

则s1(t)和s2(t)二者的互功率谱为:

Ss1s2(f)=s1(f)·s2*(f)=|s1(f)|·

|s2(f)|·eiΔφ(f)

(5)

式中:Δφ(f)=φ1(f)-φ2(f)，表示两道信号在频率为f时的相位差。

通过式(5)即可以从互功率谱中计算出单频波的相位差Δφ(f)。若2个检波器间距d2-d1记为Δx，则该频率的相速度v(f)可以表示如下:

(6)

利用式(6)就可以依次计算各个频率f的面波的相速度值，进而得到这2个检波器之间的频散曲线，最后通过反演就能得到这条频散曲线下方的横波速度结构。对记录中任意相邻的检波器组合进行SASW处理，并联合所有相邻检波器处理结果就能得到排列下方的二维横波速度剖面，最终获得每个检波点的静校正量。

2 模拟数据效果测试

相对于常规面波处理技术，该研究提出的静校正方法大大提高了横向分辨率，P-SV转换波的重点在于计算横波静校正量，因此面波静校正技术的核心就是反演资料覆盖区的二维横波速度剖面。常规面波成像方法通常基于多道面波分析进行处理，得到的结果是多道覆盖范围内的综合速度结构。以一组模拟炮集记录为例，该模型横向长为60 m，深度为40 m，设置炮点位于地表横坐标 0 m 处，并设置一直立断层在40 m位置处(如图1所示)，检波器布设在横坐标10～60 m内，共51个，道间距1 m，最小偏移距 10 m，检波器采样间隔 1 ms。图2a所示为一个模型的51道检波器的模拟记录，利用F-K变换法对其进行处理，可以得到这一组记录的频散能量谱(如图2b所示)，观察频散能量谱可知，面波具有多模式(基阶和高阶)发育的特征。对谱中的能量峰值进行识别就可以提取出频散曲线，对频散曲线进行反演即得到横波速度结构，然而这样得到的横波速度结构反映的是排列覆盖范围内地层的综合响应，无法获得具体的某一检波点下方的横波速度结构，因此也就无法计算独立检波点的静校正量。

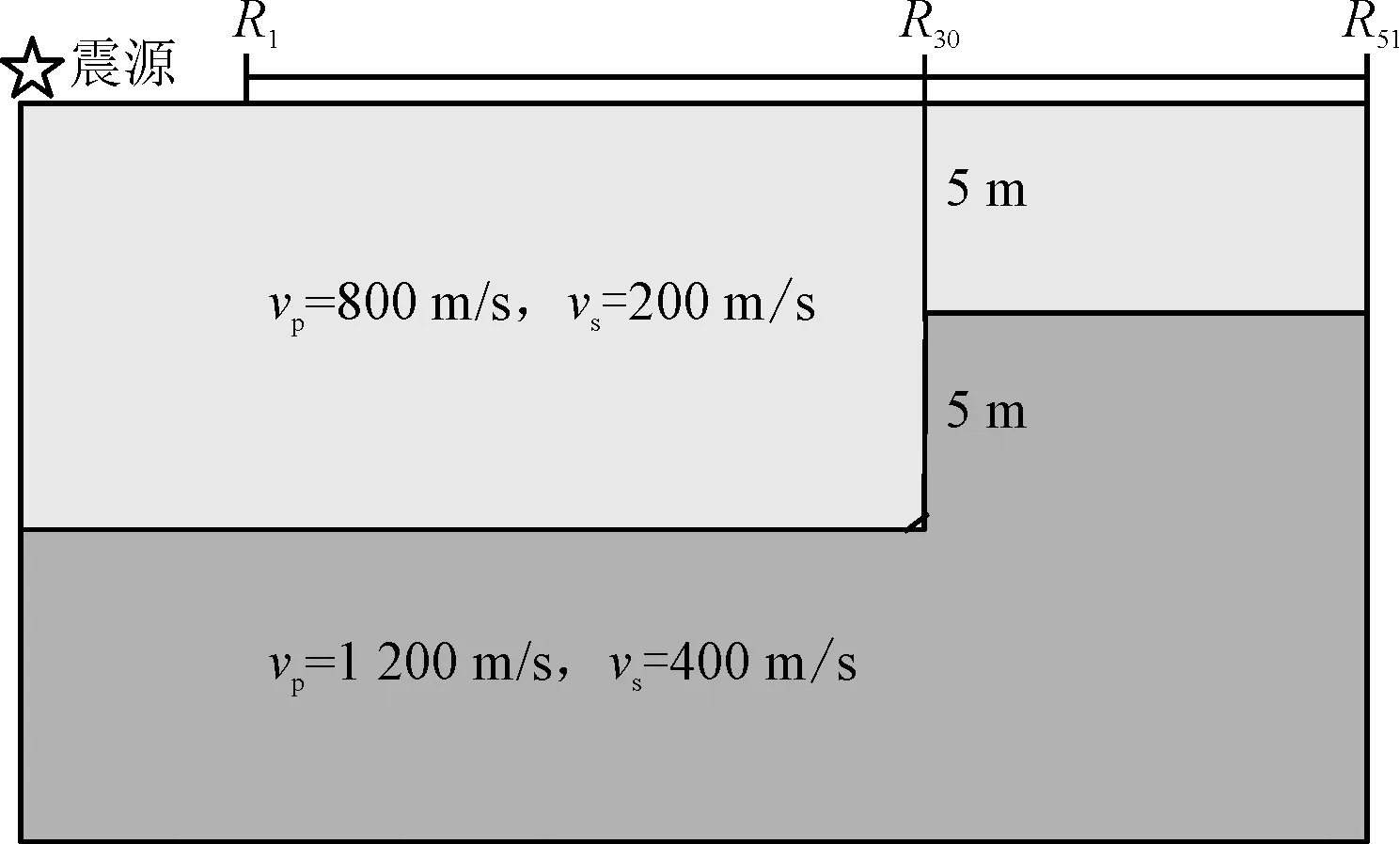
图1 断层理论模型

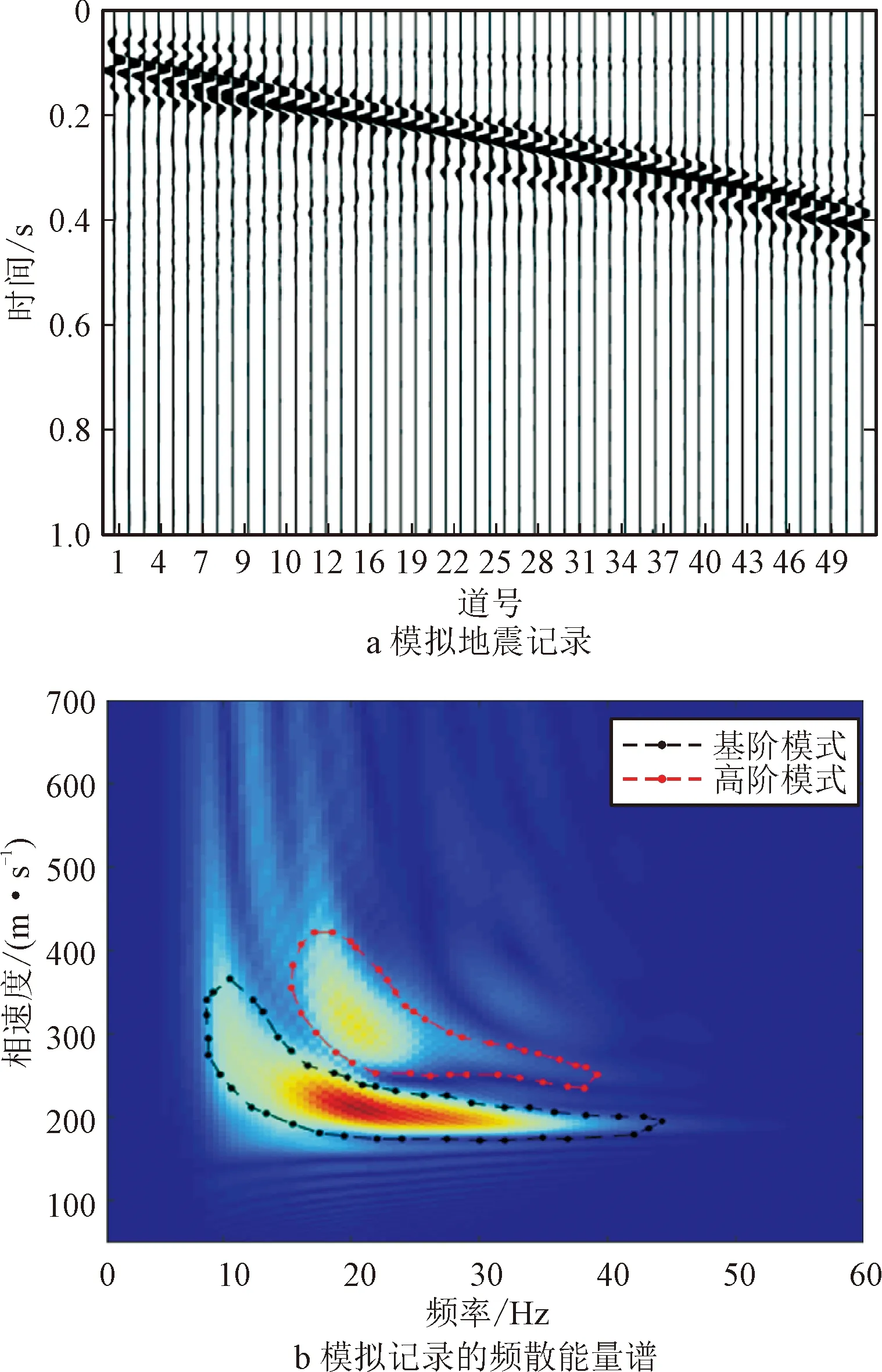
图2 51道检波器的模拟记录及其频散能量谱

利用该研究提出的改进方法进行处理，先对波场进行分离获得面波记录(如图3a所示)，然后通过SASW方法计算所有相邻检波器之间的频散曲线，由51道记录可以得到50条频散曲线(如图3b所示)。图3b中的红色和绿色点状线表示断层左右两侧地层对应的理论频散曲线。

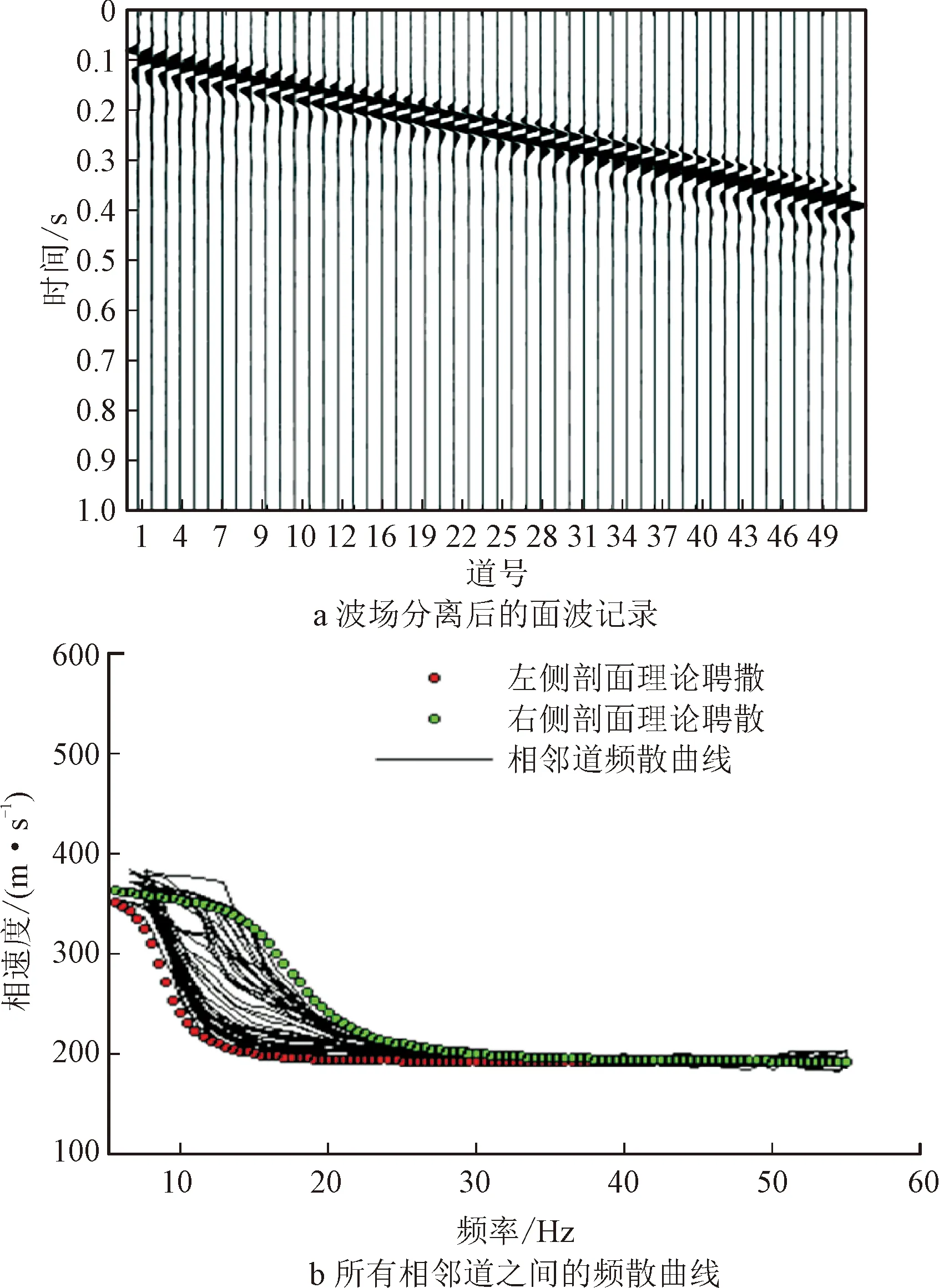
图3 波场分离后的面波记录及其频散曲线

通过上述计算所得的相邻道频散曲线，就可以反演排列下方地层的二维横波速度剖面(如图4所示)，进而建立各检波点的横波速度结构，获得每个检波点独立的横波静校正量。相比传统面波静校正方法一个排列仅能得到单点的一维横波速度结构，该文方法将横向分辨率提高到1 m级，有效提高了处理的精度。

图4 横波速度剖面

3 实例分析

该研究应用改进面波技术对鄂尔多斯盆地某研究区采集的实际转换波资料进行静校正处理。改进面波处理方法的核心在于获得高精度的覆盖层横波速度结构，利用SASW技术计算相邻道的频散曲线，进而反演相邻道下方的横波速度结构，提高速度模型的横向分辨率。

根据改进面波技术的原理，对实际资料的静校正处理可以具体分为以下几个步骤:①波场分离，利用数学变换对面波波场进行分离与重建；②相邻道频散计算；③单点横波速度结构反演；④生成横波速度剖面；⑤单道静校正量计算；⑥资料静校正。

实际资料各炮记录通过81道检波器接收，道间距为10 m，排列长度800 m，采样间隔1 ms。图5a为某炮激发的81道共炮点道集记录，可见明显的面波能量，该记录已经进行了炮点静校正，只有各个接收点的横波静校正量需要求取。

首先进行第①步的处理，利用改进的F-K变换对该记录进行处理，分离其中的基阶模式面波信号，然后利用F-K逆变换重建得到面波记录(如图5b所示)，在重建的单炮记录中面波以外的其他信号得到了压制。由于面波传播速度较慢，由图5b可见在第50道之后的检波器已无法记录到完整的面波波形，因此，该研究以前49道记录为对象进行静校正量的计算。

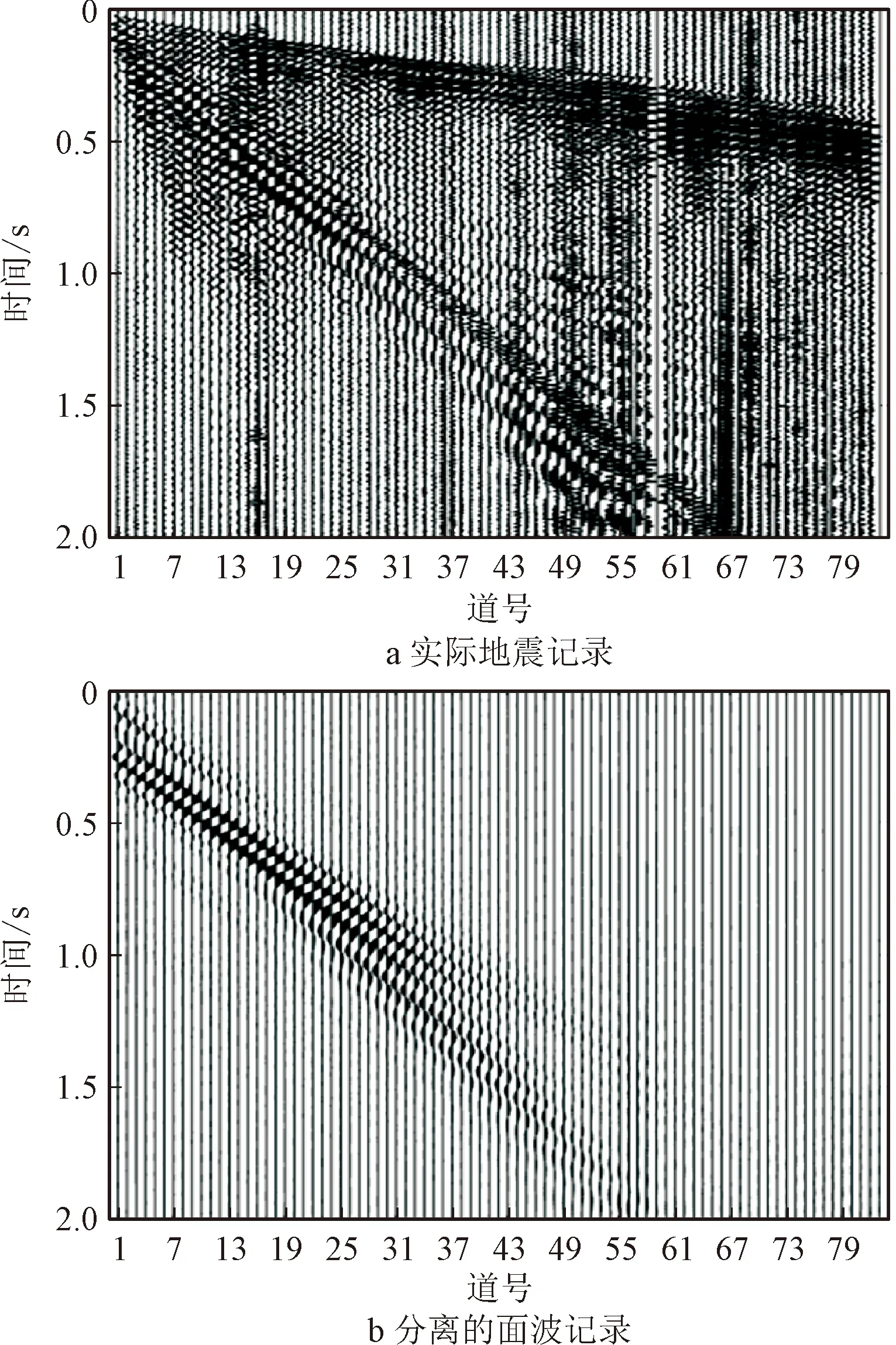
图5 实际地震记录及分离的面波记录

图6所示为对分离出的面波波场的第3道至第17道记录进行局部放大。在面波分离重建后，进行第②步处理，计算相邻检波点之间的频散曲线，以第9道和第10道为例，利用SASW方法对这两道的数据进行处理，即得到这两道中点处的频散曲线(如图7所示)。然后利用同样的方法对任意相邻的检波点的数据进行处理，获得48条频散曲线。

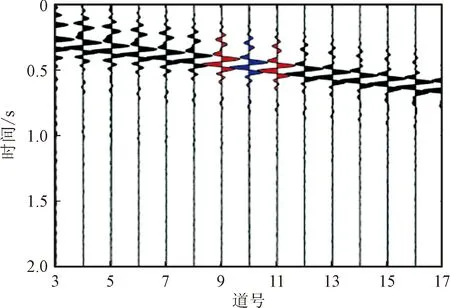
图6 道集局部面波记录

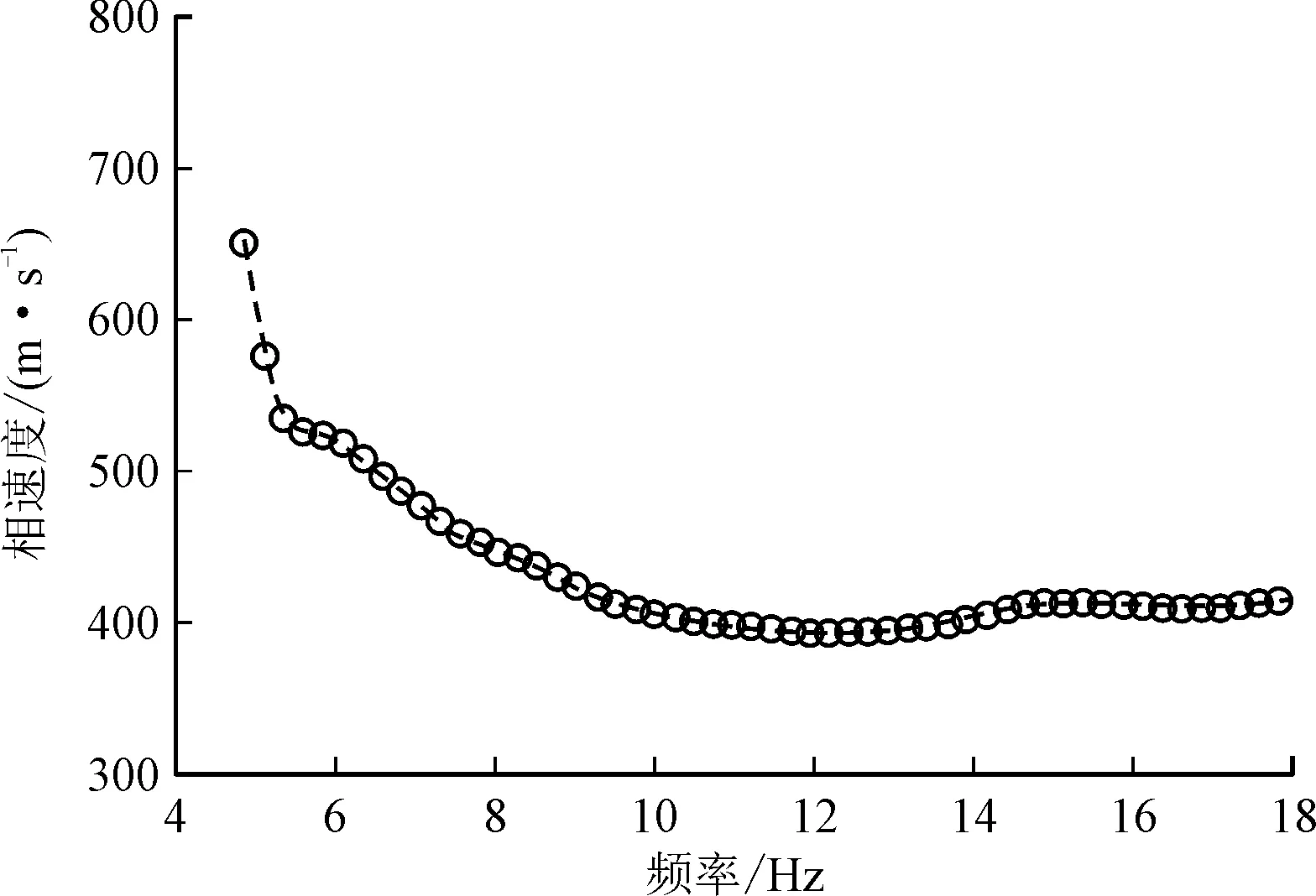
图7 第9道和第10道记录的频散曲线

获得频散曲线后进行第③步，计算每个频散曲线对应的横波速度结构。该研究利用Lei等[19]提出的遗传-阻尼最小二乘联合反演方法对频散曲线逐个进行反演，即可得到表示各组相邻道之间地层的一维横波速度结构。该横波速度结构所代表的相邻检波点之中点位置处的地层结构。然后联合各个相邻检波点下方的横波速度结构就得到了完整的横波速度剖面，即第④步，该剖面反映了前49道覆盖范围的地层横波速度结构(如图8所示)。

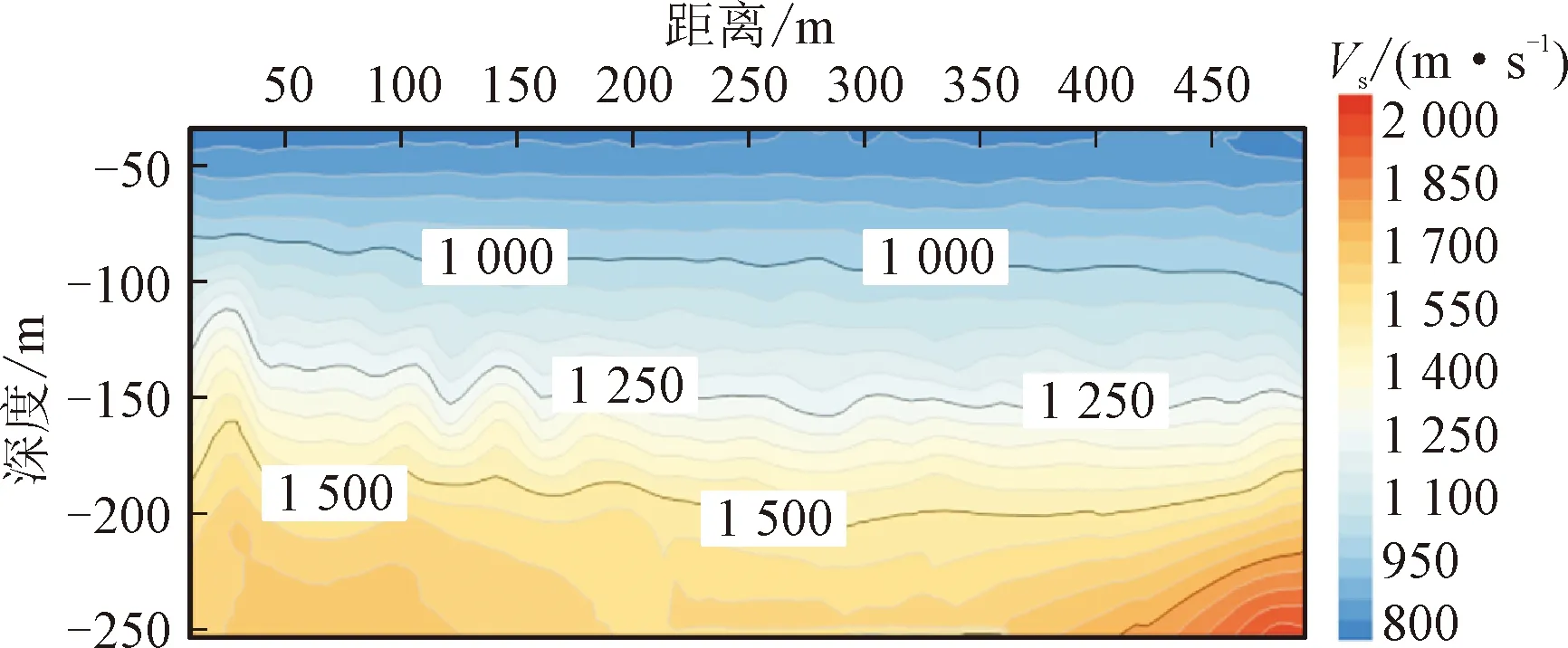
图8 横波速度剖面

第⑤步为计算单道静校正量。根据二维剖面结构，设定转换波横波静校正的横波替换速度为1 500 m/s，根据每个检波点在速度剖面上所在位置即可以计算出该检波点的横波静校正量。以前49道检波点的横波静校正量平均值为参考，将各检波点的横波静校正量减去平均值，就得到这个道集中能够提取面波范围内(0～500 m)的检波点的静校正曲线(如图9a所示)。通过曲线可以看出，横波静校正量的变化幅度约为12 ms。相比传统多道面波处理方法直接计算的静校正量，其横向分辨能力得到了有效提高。

得到各道的静校正量后，就可以进行第⑥步，对整个炮集记录进行静校正处理。图9b为静校正后的结果，可见同相轴的连续性相比校正前得到了改善。

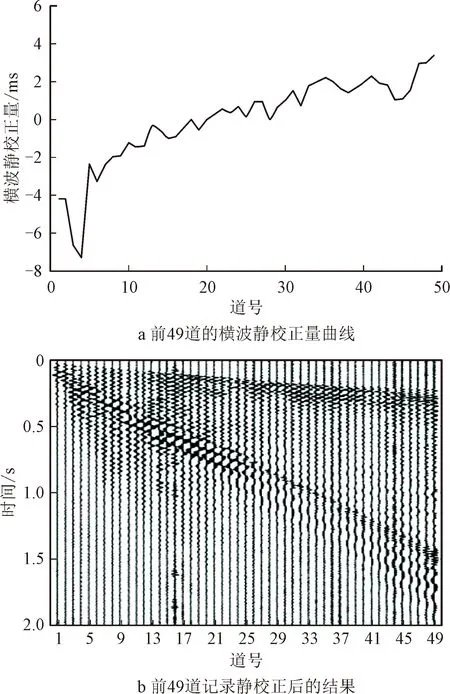
图9 前49道的横波静校正量曲线及记录静校正后的结果

4 结论

针对面波静校正法无法获得独立检波点的静校正量的难题，该研究提出将F-K变换和SASW方法相结合，对面波静校正技术进行改进。

1)将P-SV转换波资料中的面波记录单独分离出来，并计算邻近检波点之间的频散曲线，进而反演各个检波点下方的横波速度结构，可以获得各个独立检波点的横波静校正量，有效提高了面波静校正方法处理的精度。

2)在实际转换波资料处理中，由于面波传播速度较慢，一个共炮点道集会存在部分较大偏移距的检波器无法记录到面波信号的情况，因此在利用该文方法时应注意静校正量的计算范围是面波能够被记录到区域内的检波点。

3)面波具有多模式发育的特点，利用SASW技术计算多模式面波的频散曲线，反演多模式频散曲线获得各检波点的横波静校正量，能够进一步提高处理的精度，也是下一步研究的重点。