具有优先权服务的排队模型及其应用
2021-07-03丁可昕
李 晖, 丁可昕
(沈阳大学 经济学院, 辽宁 沈阳 110041)
排队论,又名随机服务系统理论,是运用数学语言描述顾客的到达方式和服务台的运行模式,通过建立模型进行统计学研究,得到该系统中具有现实应用价值的性能指标(等待时间、排队长度、忙期长短等)的数学理论.排队论是运筹学的一条重要分支学科,它的基本思想最初是在1910年由丹麦电话工程师A. K·埃尔朗解决自动电话设计问题时形成的,当时称为话务理论.1935年,费勒引进了生灭过程建立排队模型,更好地描述顾客在队列中的行为.第二次世界大战期间及二战以后,排队论在运筹学中的重要性与日俱增.经过漫长的发展过程,排队论已经成为一门实际应用性很强的学科.随着研究的深入,排队理论得到更广泛地应用.对通信系统、网络设计、计算机储存、物流调度的研究都可以通过排队模型来描述.应用较为广泛的排队模型主要有M/G/1模型[1-2]、M/M/1模型[3-4],并用MATLAB进行数值模拟[5-8].
本文主要研究在经典M/M/1排队模型的基础上,顾客按照泊松过程到达,形成一个单服务器队列,其速率用单位时间内的λ次到达表示.服务台按照FCFS(为先到达的顾客服务)原则为顾客服务,接受完服务的顾客遵循伯努利分布,以概率α(0<α<1)反馈到队列重新接受服务,或以1-α的概率离开系统永不再来,反馈的顾客具有优先权.通过分析,建立稳态方程组,运用母函数和洛必达法则计算系统各项主要性能指标,再用MATLAB对系统的一些可靠性指标进行分析和研究,最后通过观察得出结论.此模型在现实中十分常见,例如病人在一个医生的就诊队列中,若第一次就诊完成后需要完成各项检查后复诊,该病人就具有优先权;或客服咨询服务中,第二次到达咨询台的消费者通常可以优先资询.
1 模型假设
1) 泊松过程.排队论中研究最早的一类到达过程,考虑单个到达的输入过程,令N(t)表示时间[0,t]内到达的顾客数,则{N(t),t≥0}是连续时间参数的随机过程,若一个服务系统中顾客的到达过程为泊松过程,那么在不同时间段上顾客到达的数量不具有相关性,在任意Δt上到达的顾客的数量的分布函数都具有泊松分布的性质.
2) 转移概率.假定过程在时间t时的状态为i,而在时间θ时的状态为j,且θ>t,则转移概率Pij(t,θ)=P{X(θ)=j|X(t)=i}.若马尔科夫链是时间齐次的,则转移概率仅依赖于时间差τ=θ-t,简写为Pij(τ)=P{X(t+τ)=j|X(t)=i},表示给定当前处于状态i,经过时间间隔τ后过程在状态j的概率.
在经典M/M/1排队系统的假设中,系统中只有1个服务台,服务台每次只能服务一个顾客,系统容量为无穷.下面将以M/M/1排队系统为例推导排队模型的主要性能指标.
2 建立排队模型
2.1 问题的提出
基础的排队模型假设系统只对顾客服务一次,现实生活中却很难找到符合这种情况的例子,研究意义很小.大部分的情况是顾客不止到达一次,例如:医院、银行、通讯、销售等服务系统,在服务台为顾客提供一次服务后,经常遇到顾客的反馈情况,即顾客会在第一次服务结束后再次来到服务台.这样,为增加顾客黏性、提高顾客满意度、扩大销售规模及消费范围、提高运行效率等,需要赋予反馈的顾客优先权,所以现实中服务台通常会对老客户提供优先服务.为了使模型应用型更强,本文选择建立赋予一部分顾客优先被服务权利的排队模型.
2.2 建立模型
本模型中有且仅有一个服务窗口,顾客的到达过程为参数为λ的泊松过程,系统按照FCFS原则为顾客服务,接受完服务的顾客有一定概率会再次进入系统寻求二次服务.本文在M/M/1排队模型的基础上,假设会出现一部分顾客再次进入系统的反馈情况:每位顾客以参数为λ的泊松过程到达等待区,服务台按照FCFS原则为顾客服务,其中服务台为首次到达的顾客提供的服务过程为参数为μ1的泊松过程;接受完服务的顾客遵循伯努利分布以概率α(0<α<1)重新进入系统寻求服务,服务台为反馈后具有优先权的顾客提供的服务过程服从参数为μ2的泊松过程.建立具有伯努利反馈的优先权M/M/1排队模型,具体的模型描述如下:到达过程中,顾客的到达过程为参数为λ的泊松过程;服务过程中,服务窗口对初次进入系统的顾客的服务过程为参数为μ1的泊松过程;优先反馈过程中,模型中有且只有一个服务窗口,服务窗口按照FCFS的原则按队列顺序为顾客依次提供服务,本次服务过程存在反馈情况,赋予反馈的顾客优先服务权,接受完服务的顾客遵循伯努利分布以概率α(0<α<1)反馈到队列重新接受服务,或以1-α的概率退出服务系统;反馈服务过程中,服务窗口对反馈后具有优先权的顾客的服务过程为参数为μ2的泊松过程,即每位顾客的服务时间T3服从指数分布.本模型中顾客的到达过程、服务台的服务过程、顾客的优先反馈过程都是相互独立的,其中到达过程和服务过程都是泊松过程,反馈过程则服从伯努利分布,所以可以通过马尔科夫链的方法对模型的状态转移概率进行分析,然后再利用母函数结合洛必达法则的方法对模型进行求解.
2.3 主要结论
令α为顾客反馈率,λ为顾客到达率,μ1为服务窗口对非优先权顾客的服务速率,μ2为服务窗口对具有优先权顾客的服务速率.
1) 系统对非优先权顾客服务状态的概率
2) 系统中对优先权顾客服务状态的概率
3) 空闲状态概率
4) 平均队长
5) 顾客的逗留时间
3 数值模拟
本节将通过若干个数值例子演示本模型中各主要性能指标的参数变化对该性能指标的影响.本文主要考察4个性能指标:系统处于空闲状态的概率、系统处于对非优先权顾客服务状态的概率、系统处于对优先权顾客服务状态的概率及平均队长.对服务窗口属性产生影响的参数为顾客的到达率、反馈率、服务台对非优先权顾客的服务率、服务台对先权顾客的服务率.
图1中3条曲线的顾客反馈率不同.从图中可以看出:顾客反馈率增大,造成系统的队列变长,单位时间内需要服务的顾客数增加,系统压力过大,则系统处于空闲状态的概率越小.在顾客反馈率和其他因素都不变时,顾客的到达率越大,系统需要服务的总人数增加,系统处于空闲状态的概率越小.现实生活中这样的例子有很多.例如,在银行柜台处理业务时,如果顾客的到达率增加,即单位时间到达的顾客数增加,那么柜员能够处于空闲的概率就越小;假设去每个柜台的顾客数一定,顾客反馈的概率越高,则柜台处于空闲状态的概率也越小,因此图1的曲线趋势符合客观规律.图2中,3条曲线代表服务台对优先权顾客的服务速率不同.从图2中可知,当其他因素不变时,服务台对非优先权顾客的服务速率越大,系统处于空闲的概率越大.因为服务台对非优先权顾客的服务速率越大,总体的服务速度就越快,因而可以更早服务完所有顾客从而进入空闲状态.当服务台对非优先权顾客的服务速率以及其他因素相同时,服务台对优先权顾客的服务速率越大,系统处于空闲的概率越大,同理,服务台对优先权顾客的服务率上升时,总体的服务速度就越快,因而可以更早服务完所有顾客从而进入空闲状态,所以图2中的曲线走势符合客观规律.
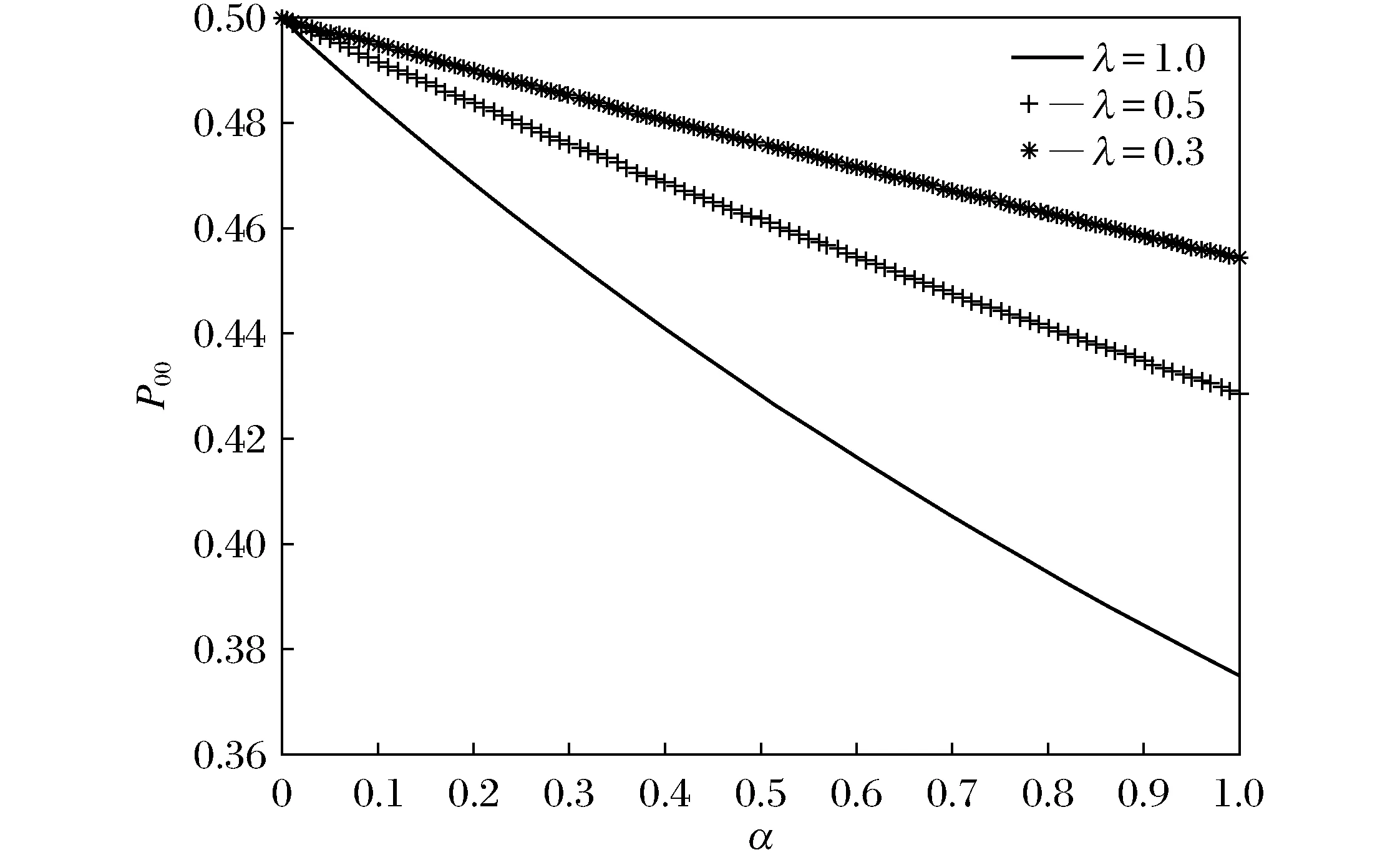
图1 空闲状态概率与顾客反馈率、到达率关系Fig.1 Relationship between idle state probability, customer response rate and arrival rate

图2 空闲状态概率与优先权、非优先权顾客的服务速率的关系
从图3中可以看出顾客的反馈率对平均队长的影响明显.随着顾客反馈率的增加,平均队长将会增大.因为当反馈率增大时,在队列中排队等待的顾客人数就会增加,从而使平均队长变大.例如在银行服务系统中,反馈的顾客越多,队伍中堆积的顾客也就越来越多,从而使队长增大,符合一般规律.从图4可以看出,随着顾客到达率的增加,平均队长将会增大.因为到达率越大,单位时间内到达的顾客数量增加,进而队列中等待的顾客数增加,因此图4的曲线走势符合实际情况.从图5可以观察到:当服务台对非优先权顾客的服务率的增加时,平均队长将会减小.因为服务台对非优先权顾客的服务率越大,单位时间内服务台能够服务的顾客数量就越多,队列中等待的顾客数减少,进而系统的等待队长减小,因此图5符合实际情况.
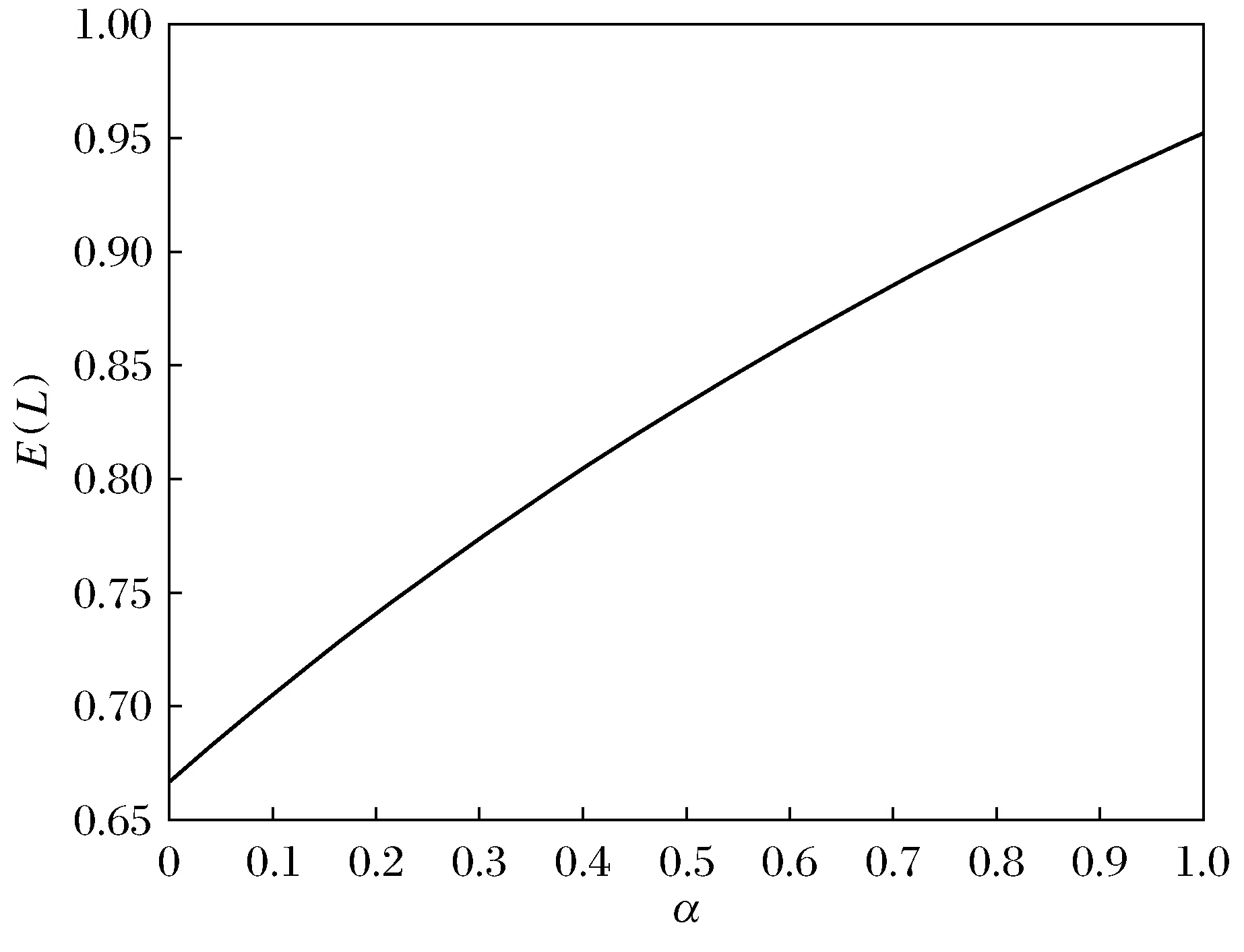
图3 系统的平均队长与顾客反馈率的关系

图4 系统的平均队长与顾客到达率的关系

图5 平均队长与对非优先权顾客服务率的关系
4 实例分析
4.1 数据处理
P县隶属于湖北省Y市,是国家级贫困县,湖北省37个重点贫困县之一,位于湖北省的中西部.在案例[9]中λ代表贫困发生率,即每年的贫困人口数;μ1、μ2表示首次脱贫率和二次脱贫率,反映一个地区政府的扶贫工作能力;α表示反馈率,即脱贫后返贫的概率.通过对调查信息进行预处理,可得排队模型所需的该地区2014年到2017年的数据,由《中国统计年鉴2018》[10]得到2017年全国的扶贫数据,所得结果如表1所示.

表1 预处理后2014—2017年P县及2017年全国的脱贫情况
4.2 模型计算
计算2014—2017年P县政府部门为处于贫困状态人员服务的概率、政府部门为处于脱贫后返贫人员服务的概率、平均逗留时间以及2017年全国的脱贫工作情况,结果如表2所示.

表2 2014—2017年P县及2017年全国脱贫工作的主要性能指标
根据计算结果可以观察到:P县政府部门处于为首次脱贫人员服务以及为返贫后再次脱贫人员服务状态的概率都逐年下降,表明该县的贫困情况正在逐年改善,需要扶贫服务的人数逐渐减少;平均逗留时间虽然逐年下降但仍远高于全国平均水平,说明该地区扶贫部门仍处于忙碌状态,工作任务繁重,需要当地政府投入比全国平均水平更多的人力、物力以及资本.该地区的扶贫工作评价指标在2016年出现断层式下降,可能与我国2016年刚进入“十三五”时期时制定的新阶段扶贫政策以及大力推广“精准扶贫”概念有关.为研究反馈率α对平均逗留时间Ws的影响,运用MATLAB进行数值分析.取反馈率α的变化在0~0.2之间,步长为0.02,绘制2017年P县在反馈率变化的情况下,该县扶贫服务窗口队列平均逗留时间的变化趋势如图6所示.

图6 顾客反馈率对平均逗留时间的影响Fig.6 The effect of customer response rate on average length of stay
由图6可以看出随反馈率α从P县0.200的水平下降到全国平均0.016的水平这一过程中,平均逗留时间Ws也逐步下降,逐渐接近全国的平均逗留水平,但仍高于全国平均水平,这是由该地区的特殊贫困情况导致的,即使返贫率与全国一致,但长期以来积累的庞大的贫困人口和阻塞的地理环境使得当地的扶贫任务依然很严峻.通过调查直接获得的数据未经计算机处理往往无法清晰地反应事物的状况.目前,我国实现全面脱贫后,基层工作人员的扶贫重心是维护脱贫攻坚的丰厚成果,减少返贫事件的发生.因此,本文通过建立适当的排队模型,用伯努利反馈来模拟脱贫后返贫的现象,用数学语言描述调查结果并计算该模型的各项性能指标.相较传统的直接观测法和不带反馈的经典M/M/1排队模型,本文的方法不仅充分考虑了P县具有脱贫后返贫的特殊情况,而且更加直观地展示了P县2014—2017年的脱贫工作情况,并与全国扶贫工作情况作比较.以上分析有助于指导接下来的工作方向,并且提醒了过去工作中的不足.
5 结 语
本文在M/M/1排队模型的基础上,研究了具有优先权的M/M/1排队模型,仿真结果表明:随着顾客的到达率、反馈率增大,系统处于空闲状态的概率将减小;而服务台对非优先权顾客和优先权顾客的服务速率的增大,会使系统处于空闲状态的概率增大.系统处于对非优先权顾客服务状态的概率与到达率成正比,与反馈率成反比;服务台对非优先权顾客的服务速率的增加会使系统处于对非优先权顾客状态的概率减小;服务台对优先权顾客的服务速率的增加会使系统处于对非优先权顾客服务状态的概率增加.系统处于对优先权顾客服务状态的概率与到达率和反馈率成正比,与服务台对非优先权顾客的服务速率的大小无关;服务台对优先权顾客的服务速率的增加会使系统处于对优先权顾客服务状态的概率减小.到达率、反馈率的增大会使平均队长增大;随着服务台对非优先权顾客和优先权顾客的服务速率的增大,平均队长会减小.在实际生活中,我们通常希望在保证顾客的到达率较大的情况下,队长尽量小(特殊营销手段的情况除外).因此,本模型为现实情况提出的建议是:提高服务台的服务速率,并且通过提高服务质量来降低顾客反馈率.
