布谷鸟马尔科夫链蒙特卡洛混合高斯地质统计学随机反演
2021-07-02王峣钧邢凯厍斌刘宇陈挺胡光岷吴秋波
王峣钧, 邢凯, 厍斌, 刘宇, 陈挺, 胡光岷, 吴秋波
1 电子科技大学资源与环境学院, 成都 6117312 太原理工大学求实学院, 太原 0300243 东方地球物理公司物探技术研究中心, 河北 涿州 072751
0 引言
地震反演是估计地下储层参数最重要的技术之一,在储层预测和岩相分类中发挥着至关重要的作用 (Castagna, 2001; Buland and Omre, 2003; Russell et al., 2003, 2011; Downton, 2005; González et al., 2008; Zhang, 2017; Yin and Zhang, 2014; Yin et al., 2015; Connolly and Hughes, 2016; Aleardi, 2018).地震反演问题依据求解方式不同,主要分为两种方式:一种是基于最优化思想的确定性反演(Aster et al., 2011; Sen and Stoffa, 2013);另一种是基于后验概率的非确定性反演(Tarantola, 2005).由于数据测量的不确定性和目标函数病态问题等原因,使得非确定性反演对地震反演问题求解更具优势(Grana et al., 2017).
非确定性反演中应用最为广泛的是基于贝叶斯框架的地质统计学随机反演.该方法利用测井数据和地震数据构建先验分布和似然函数,通过抽样获取后验概率估计未知储层参数模型(Scales and Tenorio, 2001; Ulrych et al., 2001; Tarantola, 2005).在常规地质统计学反演问题中,通常假设储层参数先验信息服从高斯分布.但是,实际地下储层由多种岩性沉积物构成,储层参数具有多峰统计特征,如果对地下介质按照相同的分布进行预测显然存在问题.研究表明,不同岩相下参数之间存在差异,但是相同岩相条件下参数近似符合高斯分布,可以采用混合高斯分布(Grana and Rossa, 2010; Dubreuil-Boisclair et al., 2012; Sauvageau et al., 2014; Amaliksen, 2014)近似刻画地下储层参数分布特征(Hastie and Tibshirani, 1996).基于这一实际情况,相关学者提出了基于混合高斯的地质统计学随机反演方法(Grana et al., 2017; Li et al., 2019),该方法可以有效提高反演精度并输出储层岩相分类结果.
现有混合高斯地质统计学随机反演方法将不同岩相数据高斯分布以加权形式进行整合,权系数按照测井数据中统计不同岩相比例确定,在反演过程中一般固定不变.这种固定初始岩相分配比例的方案可能会因测井数据分布不均和测井数据样本选择不全面等原因造成误差,进而影响最终反演结果.如果将混合高斯模型权重和储层参数、储层岩相都作为待反演参数进行同步反演,必然能够避免初始设定误差,提升反演精度.如果岩相权重变为待反演参数,则反演目标函数变为非线性函数,且反演参数变多导致多解性变强,需要提供一种稳定性更强、能较好抑制多解性的方法对目标函数进行求解.
目前随机反演主要采用马尔科夫链蒙特卡洛(MCMC)方法进行求解,其基本流程是首先在目标解空间内进行Metropolis-Hastings随机采样,根据采样前后状态求出后验概率分布,然后利用变量的马尔可夫性求出状态转移概率,当状态转移概率趋于稳定时得到最终结果.该算法主要受迭代步长、马尔科夫链长度、迭代终止条件等因素影响,一旦迭代次数或马尔科夫链长度选择不合理,会导致采样结果陷入局部最优(Geyer, 2005).如果采用目前的MCMC方法进行前文所述混合高斯模型权重和储层参数、储层岩相非线性同步反演,由于反演维度和参数进一步增加,会进一步加剧MCMC方法不稳定性.为此,本论文引入布谷鸟搜索方法和MCMC算法进行整合,实现可控步长和搜索方向的布谷鸟蒙特卡洛优化算法(CSMCMC),跳出局部最优解,获得稳定的多参数反演结果.
布谷鸟算法是2009年提出的一种新型启发式算法(Rajabioun, 2011; Yang and Deb, 2009,2010,2013)算法是根据布谷鸟幼雏不断与宿主进行适应性斗争,最终使得宿主相信的进化过程所提出的一种全局优化算法.引入布谷鸟算法,可以利用该算法中Levy飞行变步长搜索特点提升MCMC中马尔科夫链的多样性,使得抽样具有更好的动态调节性,从而提升对非线性多参数问题求解全局优化性.在本文工作中,我们基于混合高斯模型地质统计学随机反演框架,采用布谷鸟MCMC混合优化算法实现了混合高斯分布后验概率的求解,同步获得混合高斯模型不同岩相比例系数、岩相和储层参数,实现了储层岩相的精确划分,避免初始岩相比例固定导致的反演误差.通过模型和实际资料验证表明了所提出算法的有效性.
1 方法原理
1.1 混合高斯地质统计学随机反演
地震反演可以通过后验概率分布来表示(Grana et al., 2017):
(1)
其中p(m|d)是在地震数据d约束下储层参数的后验概率分布,p(d|m)是储层参数m与地震数据之间的似然函数,p(m)是储层参数的先验概率分布.在混合高斯地质统计学反演中先验信息可以分不同岩相进行描述.假设岩相可以分为K类,储层参数先验分布函数可以描述为不同岩相内储层参数先验分布概率密度之和(Li et al., 2019),即:
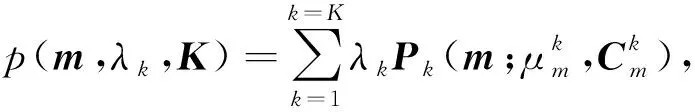
(2)
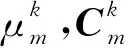
(3)
储层参数m与地震数据d之间的似然函数反映了地震数据与储层参数对应函数关系,如果可以考虑为地震波正演形式,可以描述为
(4)
其中λt是与Cm相关的常量,Cm是当前储层参数的方差,Wt是正演算子,此处代表地震子波矩阵,D是差分矩阵,分别表示为
(5)
结合上述公式可以构建混合高斯储层参数的后验概率密度函数为
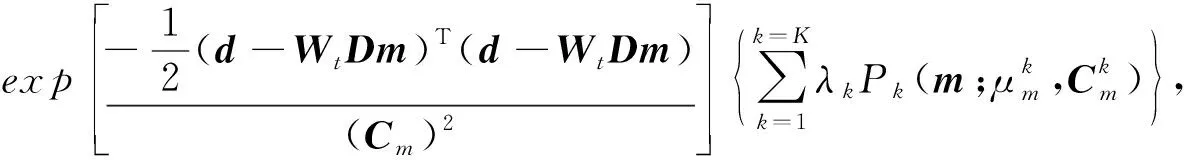
(6)
将(3)式代入并取对数并化简,可以得到后验概率密度函数的对数形式:
(7)
上述目标函数中,通常假设λk为固定值以便降低变量数量以通过MCMC方法进行求解.如果λk为未知参数,该目标函数参数量和非线性程度进一步增加,采用MCMC算法难以实现稳定求解,因此本论文提出引入布谷鸟算法与MCMC结合实现该反问题的求解.
1.2 布谷鸟搜索算法
布谷鸟搜索算法(Cuckoo search, CS)主要包括种群生成、Levy飞行搜索更新和适应性选择等几个主要步骤,其中Levy飞行有重要作用.Levy飞行与普通随机搜索的区别在于该方法是一种变步长的搜索方法,可以避免结果陷入局部最优.
布谷鸟算法流程如下:
①根据解空间维度随机生成Ω个鸟巢Mi,每个鸟巢有n个个体
Mi=(m1,m2,m3,…,mn),i=1,2,…,Ω
(8)
其中,第i个鸟巢第j个个体的初始值如下:
i=1,2,…,Ω;j=1,2,…,n
(9)
其中Lj_max,Lj_min是第j维数据的最大值与最小值.此外,我们需要设置迭代次数、发现概率等参数;
②计算鸟巢的适应度,得到最优鸟巢Mbest,适应度函数可以反映种群中个体之间性能优劣,一般情况下选择均方根误差作为评判标准;
③通过Levy飞行产生新解,对其他鸟巢位置与状态进行更新.Levy飞行代表布谷鸟位置更新,公式如下:
(10)

(11)
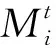
(12)
其中u和v服从正态分布,u=randnφ,v=randn,β通常取1.5.而φ可以由下式得出:
(13)

(14)
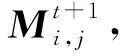

(15)
其中σ是缩放因子,σ~U(0,1),γt,t代表第t代所有个体中任意两个个体.
⑤计算种群适应度,选出新的最佳巢穴Mnewbest,将Mnewbest与上一最优值Mbest进行比较,如果满足适应度下降的接受条件,则改变当前最优值,并且更新种群适应度值.
⑥如果没有达到最大迭代次数或者没有达到误差降低标准,则返回③,直至输出最优目标解.
1.3 布谷鸟MCMC混合高斯地质统计学随机反演
本文所提算法核心是在布谷鸟的寻找当前最优巢穴的过程中采用MCMC算法中的Gibbs采样获得多条马尔科夫链,然后通过Levy飞行方式对多条马尔科夫链进行优化,最后根据多条马尔科夫链的最优适应度选择输出结果.这种多条马尔科夫链同步优化方法可以扩大样本范围,提升方法全局优化能力.此外,对于种群初始化,由于传统初始化策略使得每个初始种群都与实际参数模型分布有很大的差异,导致反演过程中收敛速度慢,考虑不采取随机初始化方式,而是利用地质统计学建模获得的储层参数初始分布作为算法种群初始解将传统布谷鸟搜索中种群初始化进行优化,使得初始化的种群仍然保留储层参数分布的大致特点.基于布谷鸟搜索(CS)和MCMC结合的混合高斯地质统计学随机反演方法(GMM-CSMCMC)流程如图1所示.具体流程为
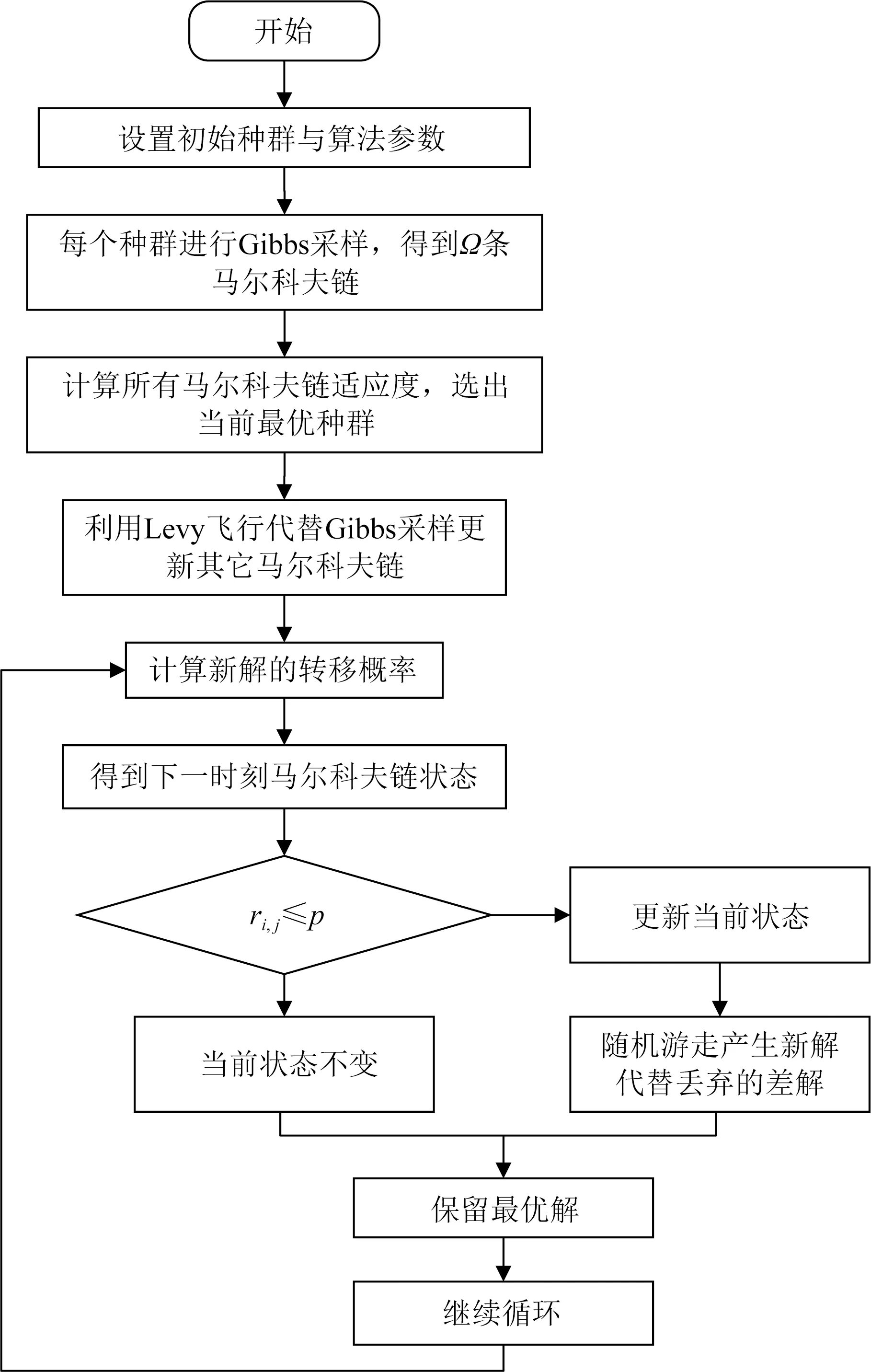
图1 基于布谷鸟搜索马尔科夫链蒙特卡洛(MCMC)混合高斯地质统计学随机反演流程Fig.1 The workflow of GMM-CSMCMC algorithm
①根据地质统计学建模方法,我们可以得到目标地层的初始分布,该模型粗略地反映地层分布,使用该结果作为反演的初始模型;
②根据地质统计学的结果进行种群初始化,即马尔科夫链初始化:
(16)
其中,i代表个体,j代表个体i的维度,m_ini是由地质统计学建模求得的地层参数分布,var_ini是地质统计学随机建模求得的对应位置的方差值,eLb是Lb长度之内的随机数,K1和K2是常数项,Lb和Ub代表下界与上界.地质统计学建模可以得到地层模型的初始分布,因此该初始化策略可以使得初始种群更加接近于实际地层参数分布;
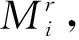
④针对所有马尔科夫链,根据适应度函数计算最优值.记第i个种群马尔科夫链的适应度为fitMi,最小的适应度为bestfitM,对应标号为Lbestfit,则该种群当前最优解Mbest=M(Lbestfit).适应度函数为
Fit(Mi)=(GMi-d)T(GMi-d)
(17)


⑥求出后验概率分布函数为
(18)
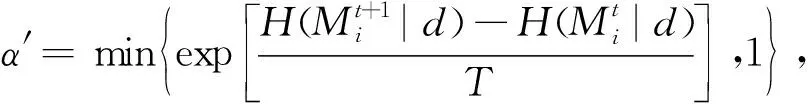
⑦如果误差没有下降到目标范围或者迭代次数不足,则迭代次数t=t+1,重复上述步骤⑤—⑥,直至迭代次数达到最大为止,输出弹性参数、岩相比例和岩相分类反演结果.
2 实验分析
2.1 模型测试
首先使用40 Hz雷克子波和真实测井数据合成记录作为实际地震数据进行测试.根据算法参数设置经验,设置初始种群个数(鸟巢数量)为25,宿主发现异常卵的概率设置为0.25.选择我国东北某工区3口井数据进行反演分析.为方便比较,此处我们将权系数固定不变的常规混合高斯地质统计学反演简记为GMM-c,权系数变化但是采用MCMC算法进行求解的方法称为GMM-v,采用新方法求解的称为GMM-CSMCMC,图2为结果对比图.
在图2中,绿色线条代表实际井数据,蓝色、浅蓝色线和红色线条分别代表GMM-c、GMM-v和GMM-CSMCMC反演结果.为了定量对比,我们还计算了3种反演方法结果与井数据相关系数和均方根误差以验证反演效果有效性,如表1所示.从反演结果与井数据的吻合程度来看,GMM-v反演结果要比GMM-c反演结果更优,而GMM-CSMCMC反演结果与井数据的吻合程度要明显优于其他两类反演方法.

表1 合成记录误差与相关系数Table 1 Error and correlation coefficient of synthetic records

图2 GMM-c (a)、GMM-v (b)、GMM-CSMCMC (c) 反演的单道结果对比Fig.2 Comparison of single trace results of GMM-c (a), GMM-v (b), GMM-CSMCMC (c) inversion using synthetic seismic records
选取第一口井岩相反演结果做对比,如图3所示.GMM-c、GMM-v和GMM-CSMCMC的岩相分
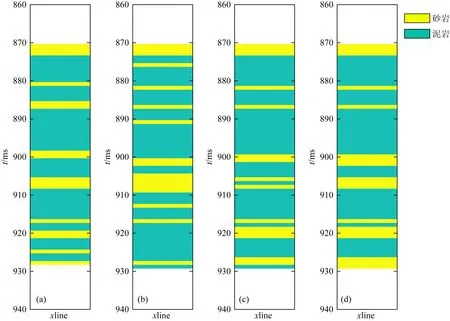
图3 井数据(a)、GMM-c反演(b)、GMM-v反演(c)、GMM-CSMCMC反演(d)的分相结果对比Fig.3 Comparison lithology results of well data (a), GMM-c inversion (b), GMM-v inversion (c), GMM-CSMCMC inversion (d)
类正确个数分别为:43,48,50,表明本文所提方法可得出更为准确的岩相分类结果.
进一步为了测试算法抗噪性,我们在合成记录的基础上添加信噪比等于10和信噪比为4的高斯噪声.单道测试结果如图4和5所示,三种反演结果与井数据的均方根误差与相关系数如表2和表3所示,岩相分类结果如图6和7所示.可以发现,在含噪声数据中,采用变权值的方法(GMM-v)反演结果要更加稳定,而GMM-CSMCMC反演结果与井数据的吻合程度要高于GMM-v,可见GMM-CSMCMC反演结果对于高斯噪声有很好的抗噪性,而GMM-c反演结果受噪声影响较大.从图6和图7岩相结果对比可以发现,添加SNR=10的高斯噪声后,不同反演结果的获得岩相分类正确个数分别为:43,45,50;在信噪比为4时不同反演结果的岩相分类正确个数分别为:46,47,50,从参数数值结果精确度与岩相分类正确个数来看,GMM-CSMCMC反演结果都是最优的,因此上述实验说明了在不同信噪比条件下,GMM-CSMCMC反演方法的抗噪性要优于其他两种方法.
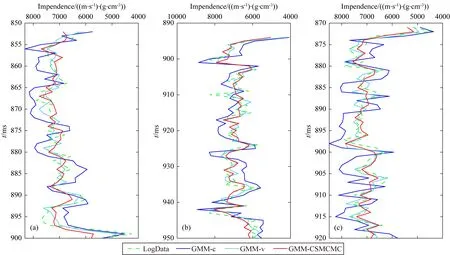
图4 添加SNR=10的高斯噪声的合成地震记录种GMM-c (a)、GMM-v (b)、GMM-CSMCMC (c) 反演结果对比Fig.4 Comparison of GMM-c (a), GMM-v (b) and GMM-CSMCMC (c) inversion results using synthetic seismic records with Gaussian noise (SNR=10)
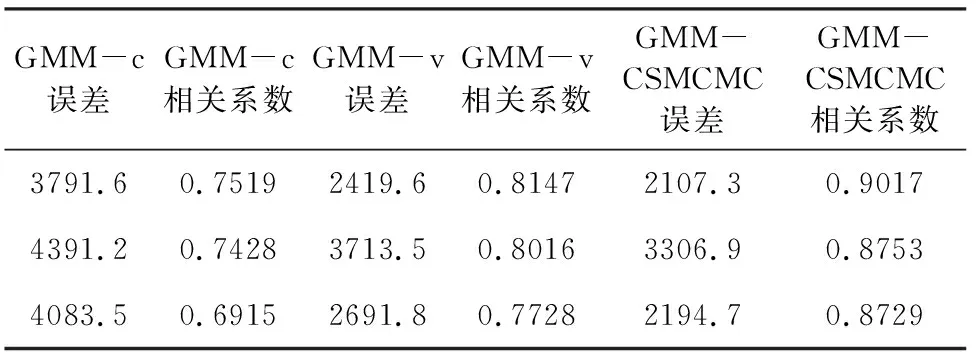
表2 添加高斯噪声(SNR=10)反演结果与真实井曲线误差及相关系数Table 2 Error and correlation coefficient of inversion results and real well curves with Gaussian noise (SNR=10)
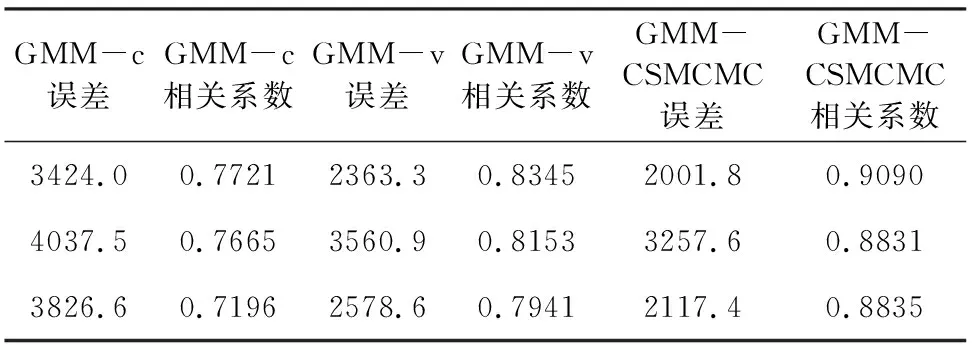
表3 添加高斯噪声(SNR=4)反演结果与真实井曲线误差及相关系数Table 3 Error and correlation coefficient of inversion results and real well curves with Gaussian noise (SNR=4)
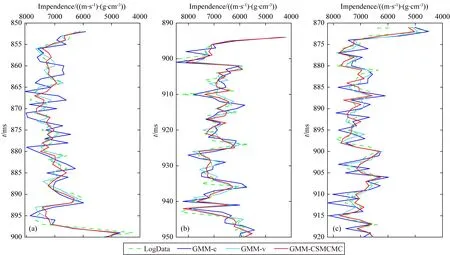
图5 添加SNR=4的高斯噪声的合成地震记录种GMM-c (a)、GMM-v (b)、GMM-CSMCMC (c) 反演结果对比Fig.5 Comparison of GMM-c (a), GMM-v (b), and GMM-CSMCMC (c) inversion results using synthetic seismic records with Gaussian noise (SNR=4)

图6 添加SNR=10高斯噪声下井数据(a)、GMM-c反演(b)、GMM-v反演(c)、GMM-CSMCMC反演(d)的分相结果对比Fig.6 The comparison of the lithology results of well data (a), GMM-c inversion (b), GMM-v inversion (c), GMM-CSMCMC inversion (d) with Gaussian noise (SNR=10)
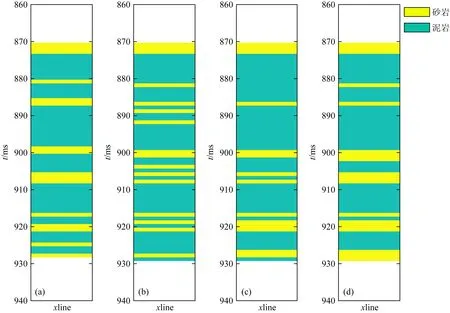
图7 添加SNR=4高斯噪声情况下井数据(a)、GMM-c反演(b)、GMM-v反演(c)、GMM-CSMCMC反演(d)的分相结果对比Fig.7 The comparison of the lithology results of well data (a), GMM-c inversion (b), GMM-v inversion (c), GMM-CSMCMC inversion (d) with Gaussian noise (SNR=4)
2.2 实际资料测试
GMM-CSMCMC反演之所以能够得到高稳定性的结果,是因为布谷鸟算法特殊的搜索方式:在前期搜索步长较大,从而可以增加种群的多样性,此时可以有效地跳出局部最优解;后期搜索步长较小,可以得到某个区域内的较高精度解,因此布谷鸟搜索是一种更方便得出全局最优解的搜索方式.为了验证该理论,我们选择东部某过井地震数据,测试GMM-CSMCMC反演方法与GMM-CSMCMC反演方法的迭代误差下降趋势,结果如图8所示.
根据图8可知,GMM-c反演与GMM-v反演误差下降趋势呈阶梯状,而GMM-CSMCMC反演误差一直下降直到稳定,能跳出由于参数设置不合理等引起的局部最优现象.可见,GMM-CSMCMC能够更为快速的下降到更低的稳态误差,因此我们可以证明GMM-CSMCMC反演方法可以得到更准确的反演结果.
为了考虑参数选择对反演结果的影响,我们进行算法参数测试.根据图9分析可知,当马尔科夫链长度过短时会导致误差下降不充分,相关系数变化不稳定,随着马尔科夫链长度逐步增加,反演结果的误差在逐渐下降,相关系数整体呈上升趋势,长度为8时误差与相关系数变化趋于稳定.根据图10分析可知,当温度下降至260 ℃附近,反演结果已经趋于稳定,说明反演过程更快达到稳定状态.综合分析可知,GMM-v反演融合布谷鸟算法后,减小了参数设置的约束,更容易得到合适的算法参数.

图8 GMM-c反演(a)、GMM-v反演(b),与GMM-CSMCMC反演(c)的误差随迭代次数变化对比Fig.8 Error vs. iteration number comparison chart of GMM-c inversion (a), GMM-v inversion (b), and GMM-CSMCMC inversion (c)

图9 不同长度马尔科夫链GMM-CSMCMC单道反演结果的误差(a)与相关系数(b)曲线Fig.9 Errors (a) and correlation coefficient curves (b) of inversion results with Markov chains of different lengths of GMM-CSMCMC inversion

图10 GMM-CSMCMC反演不同温度单道反演结果的误差(a)与相关系数(b)曲线Fig.10 Errors (a) and correlation coefficient curves (b) of inversion results with different temperature of GMM-CSMCMC inversion
在算法中初始种群个数(鸟巢个数)的不同也会导致结果出现偏差.为了保证算法效率,设置参数时不宜过大.我们选择其中一口井的数据,分别对初始种群个数为5,10,15,20,25,30的参数进行测试.根据图8c所示,当迭代次数在200左右时误差已经趋于稳态,因此此处迭代次数设置为200.对于每个初始种群个数,都记录每次反演结果与实际测井曲线的均方根误差,然后进行10次平均,用来比较判断种群个数对结果的影响,如表4所示.可以发现,初始种群个数过大(30)或者过小(5),结果误差都比较大,当鸟巢个数为25时,结果的误差最小.通常实际计算时初始种群个数可在25附近调节.

表4 不同种群个数的结果误差表Table 4 Results error table for different population numbers
宿主发现异常卵的概率不同,结果也会有所不同.因此我们在选择最佳种群个数的基础上,选择不同的发现异常卵概率进行结果测试.与初始种群个数相似,对于每个发现异常卵概率,进行10次独立测试,通过比较每个发现异常卵概率得到的平均误差,来判断最优发现异常卵概率.在本次实验中,经过测试可以设置该参数值分别为0.25,0.5,0.75(表5),可以发现,概率为0.25时,结果误差最小.

表5 宿主发现异常卵不同概率的结果误差表Table 5 Error table of results for hosts with different probability of finding abnormal eggs
根据图8c所示,迭代次数在200左右误差下降速度已经很缓慢,所以在实际运用中,可以将迭代次数设置为200.因此,GMM-CSMCMC反演方法建议最佳参数设置如表6所示.

表6 反演最佳参数设置表Table 6 Optimal parameter setting table
进一步对我国东部某实际工区进行测试,该工区数据范围为iline∈[1,142],xline∈[1,110],属于碎屑岩储层,地震采样间隔1 ms,岩相主要为砂泥岩.根据测井数据统计可以得出平均砂岩、泥岩两种岩相分别所占比例为λ1=0.38,λ2=0.62,并将该比例作为初始值代入算法进行计算.由于MCMC方法属于全局优化算法,对初始岩相比例依赖性不大,此处初始岩相比例也可自由设置,对结果影响不大.对于三种不同的反演方法,我们设置相同的共有参数,得到的结果过井剖面如图11所示.图11a是过井地震剖面图,图11(b,c,d)分别是GMM-c、GMM-v和GMM-CSMCMC反演的阻抗结果.从剖面分析可以发现,三种方法都能得到相比地震数据更高分辨率的波阻抗反演结果.相较于GMM-c和GMM-v反演结果而言,GMM-CSMCMC反演剖面参数横向展布更加均匀,信噪比更高.为了进一步验证本实验结果正确性,我们选择该剖面对应的实际地震数据,与三种反演结果的合成地震数据进行对比.图12(a—c)分别为 GMM-c、GMM-v和GMM-CSMCMC反演结果的合成地震剖面.与图11a实际地震剖面对比可看出,GMM-v和GMM-CSMCMC方法得到结果合成地震数据剖面与实际地震剖面更接近.为了定量化描述这一结论,我们计算三种结果合成数据剖面与实际地震数据剖面之间的均方根误差,结果见表7.根据定量分析可以看出,GMM-CSMCMC反演结果的合成地震数据误差最小,最接近真实地震剖面,表明考虑岩相比例变化并采用新方法求解得到结果更符合实际地质情况.此外,针对三种反演方法得到岩相分类结果进行了对比,结果如图13(a—c)所示,分别表示GMM-c、GMM-v和GMM-CSMCMC反演的岩相分类结果,岩相比例见表8.从岩相剖面对比可以看出,GMM-CSMCMC方法得到结果岩相信噪比更高.
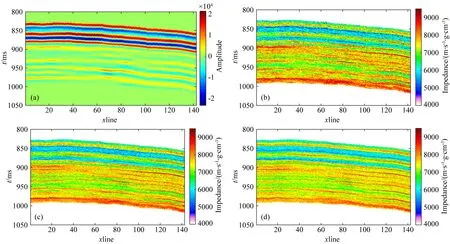
图11 实际地震数据剖面(a)、GMM-c反演(b)、GMM-v反演(c)与GMM-CSMCMC反演过井剖面图(d)Fig.11 Profile of seismic data (a), GMM-c inversion (b), GMM-v inversion (c) and GMM-CSMCMC inversion profile (d)
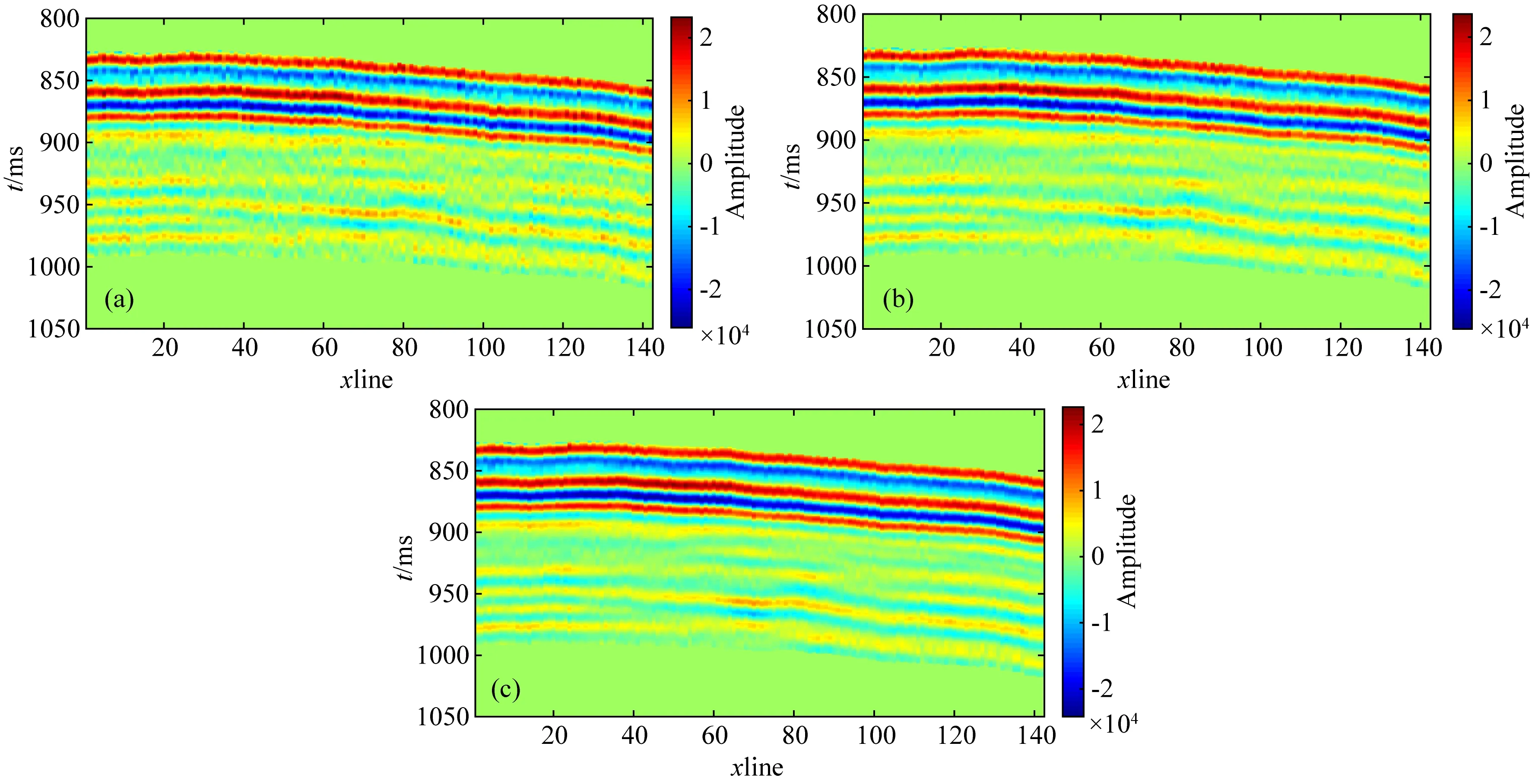
图12 GMM-c反演结果的合成地震剖面(a)、GMM-v反演结果的合成地震剖面(b)与GMM-CSMCMC反演结果合成地震剖面(c)Fig.12 Synthetic seismic profile of GMM-c inversion results (a), GMM-v inversion results (b) and GMM-CSMCMC inversion results (c)

表7 三种合成地震剖面与实际地震剖面的均方根误差表Table 7 RMSE table of synthetic seismic profiles and actual seismic profiles
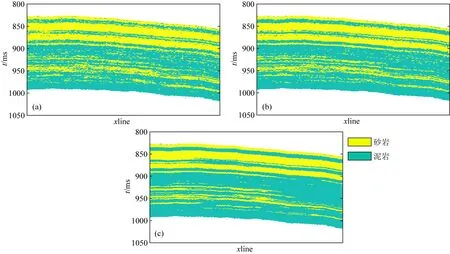
图13 GMM-c反演(a)、GMM-v反演(b)与GMM-CSMCMC反演(c)剖面岩相分类图Fig.13 Lithofacies classification map of GMM-c inversion (a), GMM-v inversion (b) and GMM-CSMCMC inversion (c)

表8 最终岩相比例表Table 8 Final lithofacies proportion table
为进一步定量说明问题,本文抽取上述剖面中三口井反演结果进行分析,反演波阻抗结果如图14所示,定量分析如表9所示.由三口井波阻抗反演对比图可见,GMM-CSMCMC反演与井数据的吻合程度高于GMM-c反演、GMM-v反演与井数据的吻合程度.从定量对比可以发现GMM-CSMCMC反演结果误差要小于GMM-c和GMM-v反演结果的误差,相关系数也更高.为了说明岩相分类精度,选择第一口井数据岩相反演结果进行对比,如图15所示,可以发现三种反演方法得到岩相分类正确数分别为:47,49,50,GMM-CSMCMC反演准确度最高.综上所述,从各种评价指标分析,GMM-CSMCMC反演要优于其他两种反演效果,验证了本文所提方法的有效性.
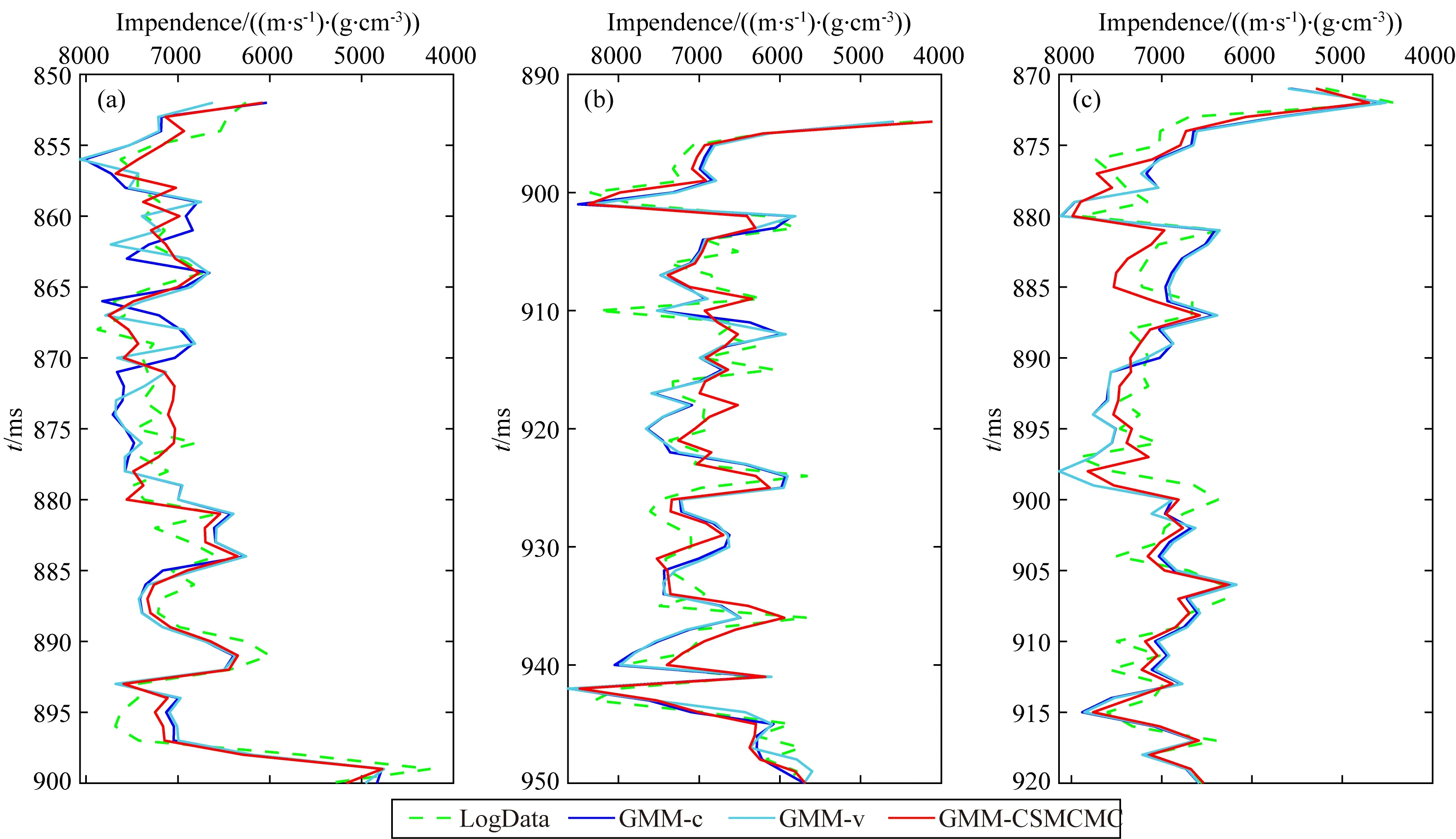
图14 三口井GMM-c、GMM-v、GMM-CSMCMC过井反演结果对比Fig.14 Comparison of GMM-c, GMM-v, GMM-CSMCMC inversion results for three well logs
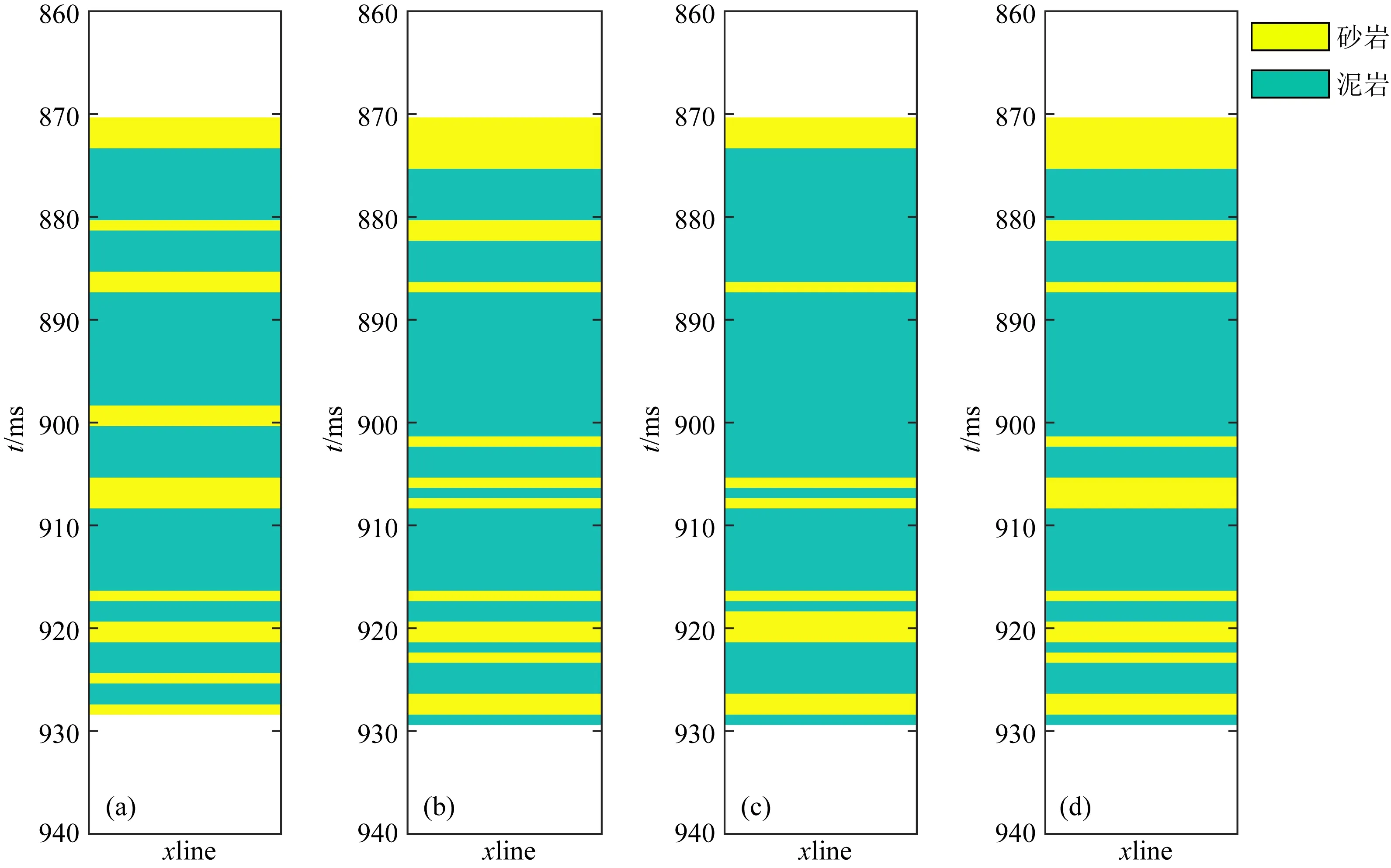
图15 真实井数据岩相分类(a)、GMM-c反演(b)、GMM-v反演(c)、GMM-CSMCMC反演(d)的岩相分类结果对比Fig.15 Comparison of lithology of real well data(a), GMM-c inversion(b), GMM-v inversion(c), GMM-CSMCMC inversion(d)
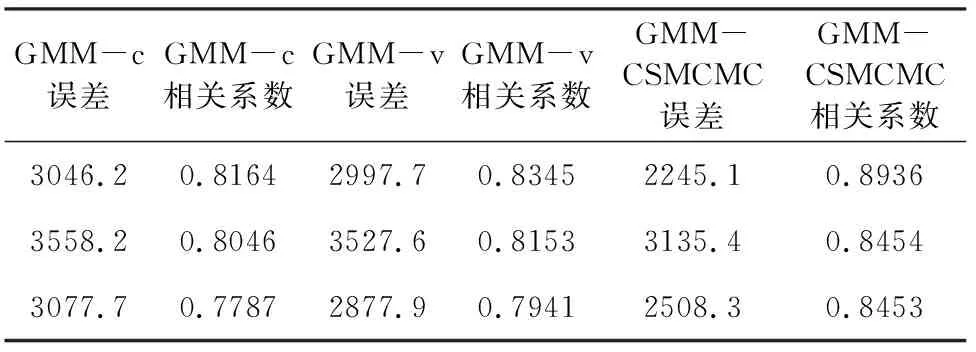
表9 单井反演结果与真实井误差及相关系数Table 9 Single trace inversion results with real well errors and correlation coefficients using actual seismic data
3 结论
论文提出了基于可变岩相参数的混合高斯模型地质统计学反演框架,同时输出岩相和波阻抗反演结果.针对该反演目标函数的高维多参数非线性求解问题,提出了布谷鸟搜索和MCMC混合的全局优化求解算法.通过实验对比发现基于变岩相的混合高斯模型地质统计学反演可以得到精度更高的岩相和反演结果.论文所提出的布谷鸟蒙特卡洛马尔可夫链优化算法利用Levy飞行可实现可变步长搜索过程,在算法前期搜索过程中,较大步长搜索增加了种群多样性,算法后期搜索过程中步长变小,可提高搜索精度,便于在某个小区域内得到全局最优解,因此可以避免结果陷入局部最优解.综合所提出算法和变岩相混合高斯统计学反演目标函数,可得到更精确的岩相分类和储层参数反演结果.
致谢感谢东方地球物理公司提供实际数据和指导.
