一种民用小型无人机的射频指纹识别方法 *

蒋 平 ，谢跃雷

(桂林电子科技大学 宽带与智能信息技术中心，广西 桂林 541004)

0 引 言

随着民用小型无人机技术的高速发展，因操作人员缺乏安全意识，无人机侵入机场、军事基地、重要会场的违法事件屡有发生，给国家和社会带来了严重的安全隐患[1]。因此，加强对无人机的管控势在必行，而如何探测和发现无人机则是实现管控的第一步[2-4]。

探测和识别无人机的射频信号，是发现无人机的一种有效方法[5-7]。民用小型无人机的射频信号可分为遥控信号及图传信号，遥控信号用于无人机控制，通常采用跳频方式的扩频通信信号，而无人机图传信号则用于空中拍摄视频的传输，通常采用正交频分复用技术(Orthogonal Frequency Division Multiplexing,OFDM)的调制信号。

许多学者通过无人机遥控信号对无人机进行检测及识别，其中文献[5]给出了一种基于无线电信号特征识别的无人机监测算法设计，从跳频信号及图传信号方面对无人机进行探测，但未给出具体算法分析及更近一步的实现原理；文献[6]提出基于软件无线电平台的无人机入侵检测，通过无人机跳频信号特征对无人机进行检测与识别，能在15 m内检测无人机的存在，但该方法无法完成对无人机具体型号的区分；文献[7]采用对跳频信号进行图像分类的方式完成无人机信号的检测与识别，并取得了较好的识别效果，但跳频信号易受噪声淹没造成信号丢失，导致其不能较好地进行参数估计，从而无法有效区分无人机型号，并且该方法不能区分个体。

针对以上检测及识别所存在的缺陷，本文采用射频指纹提取法(Radio Frequency Distinct Native Attribute，RF-DNA)[8-9]对遥控信号进行检测及识别。首先零中频接收机对无人机遥控信号进行侦收，随后检测遥控信号瞬态部分起始点并进行统计特征提取，构造RF-DNA指纹特征并对其进行特征降维，最后由多支持向量机(Support Vector Machine,SVM)分类器对无人机型号以及同一型号的个体进行区分。

1 无人机遥控信号模型

对于无人机的检测与识别，需从信号方面进行分析。民用无人机遥控信号通常采用跳频方式进行扩频通信[10-11]，因此遥控信号即为用于无人机控制的跳频信号。跳频信号因其具有较好的抗干扰能力，广泛用于通信对抗方面，而民用无人机的控制也在其列。

信息数据m(t)通过信号调制器得到d(t)，发射的跳频信号为

S(t)=d(t)SFH(t) 。

(1)

式中：SFH(t)是跳频信号，表达式为

(2)

式中：N为频点个数；A为振幅；wT为宽度为Th的矩形窗，Th为跳频信号的跳频周期；f0,f1,f2,…,fk为调频频率集；φn为初始相位，n=0,1,2,…,N-1。

实测无人机遥控信号离散数据由Cool Edit Pro软件打开，如图1所示。

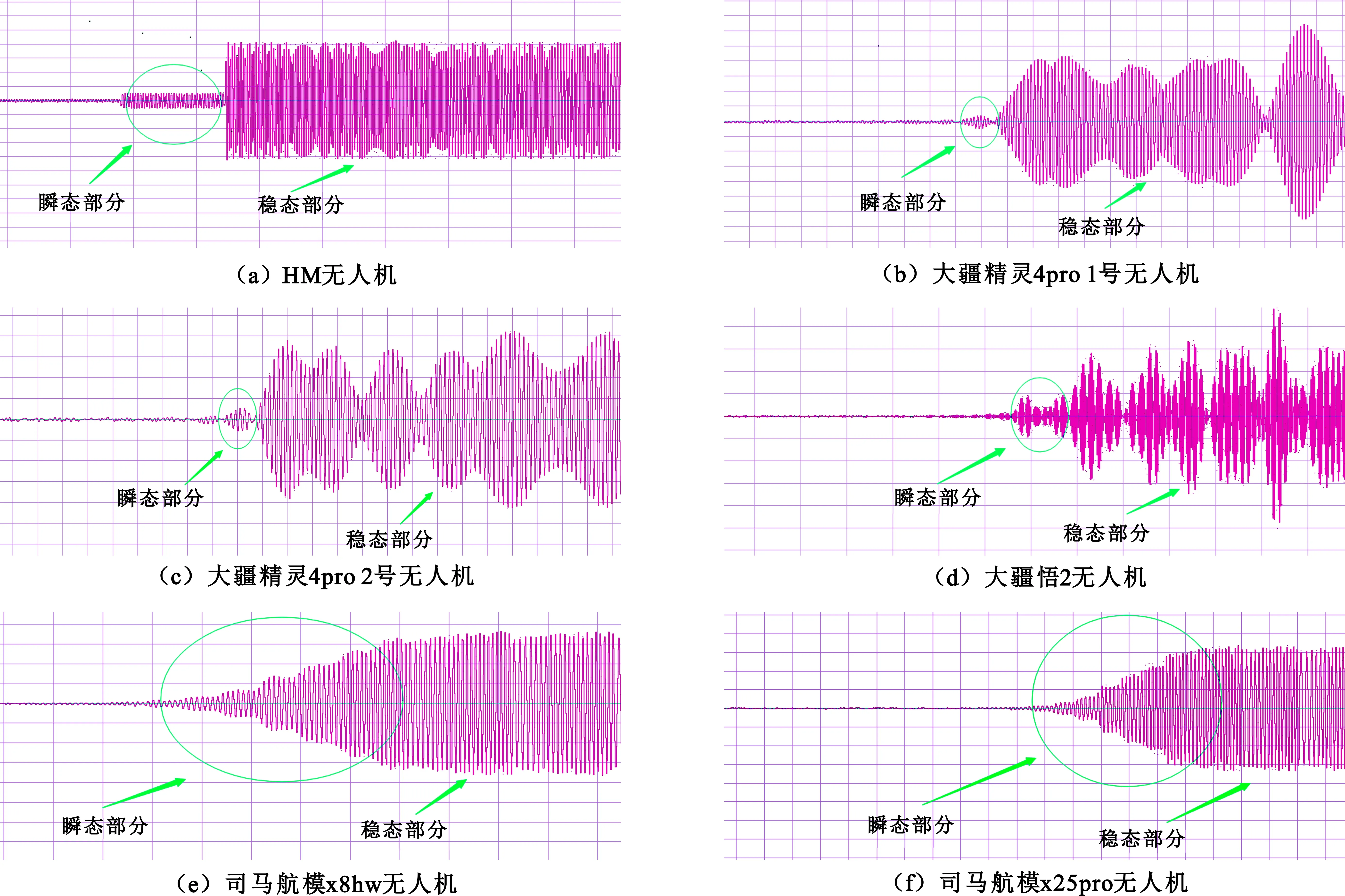
图1 无人机遥控信号瞬态及稳态图

从图1可知，不同厂商无人机机型具有不同瞬态部分,但同一无人机型号的瞬态部分不易区分。

本文主要基于民用无人机遥控信号瞬态部分进行研究。对于无人遥控信号瞬态部分，因无人机发射设备硬件特性不同，导致瞬态部分出现细微差异，这些差异主要由无人机发射设备系统中的分立器件、信号混频器、功率放大器、数模转换器、滤波器、锁相环等多种硬件设备产生。瞬态部分不携带数据信息，只与硬件设备本身的特性有关，具有唯一性，所以常对瞬态部分进行分析。瞬态部分存在于信号功率由零变为额定功率之间，所以一般存在发射设备开关机时刻。因此采集发射设备的瞬态部分具有一定难度，尤其体现在硬件接收设备[12]。

由于无人机遥控信号采用跳频通信方式，在操控无人机期间，信号会不停经历由功率零到额定功率的变化过程，所以采用RF-DNA方法对无人机遥控信号进行检测及识别是一个有效的方法。

2 基于RF-DNA的无人机识别

2.1 RF-DNA特征提取

RF-DNA方法是近年来较为关注方法之一，最早由美国空军技术学院Temple等人提出。该方法是一种采用统计方法生成射频指纹(Radio Frequency Fingerprinting,RFF)特征的计算框架，可分成瞬态信号子区域划分、瞬态信号基础特征生成和瞬态信号统计特征生成。

对于该算法，对其分步骤描述。

Step1 对接收信号X(n)进行希尔伯特变换，得其解析式：

X(n)=I(n)+jQ(n) 。

(3)

式中：I(n)、Q(n)为正交信号。

Step2 求信号瞬时幅度a(n)、瞬时相位p(n)和瞬时频率f(n)：

(4)

(5)

(6)

Step3 为了消除零中频接收机偏差对瞬时信号影响，对瞬时信号进行中心化处理：

ac(n)=a(n)-ua，

(7)

fc(n)=f(n)-uf。

(8)

对于瞬时相位，需在中心化处理之前对瞬时相位中的非线性分量进行逐个滤除，以保证特征提取质量:

pnl=p(n)-2πuf(n)Δt，

(9)

pc(n)=pnl(n)-upnl。

(10)

式中：ua、uf表示瞬时幅度与瞬时频率的均值，Δt表示采样时间间隔,upnl为消除非线性分量后瞬时相位平均值,pnl表示非线性相位响应,ac(n)、fc(n)、pc(n)分别为中心化处理后的瞬时幅度、瞬时频率、瞬时相位值。

Step4 将以上所求三个瞬时特征ac(n)、fc(n)、pc(n)进行分区，并对其求特征值。

这里特征值有两种方式，第一种为求三个时域瞬时信号的方差、偏度和峰度，第二种为求三个时域瞬时信号的标准差、方差、偏度和峰度。

标准差:

(11)

方差:

(12)

偏度：

(13)

峰度：

(14)

式中：Nx表示中心化数据xc(n)的长度，u表示xc(n)的均值。

Step5 求其特征向量，因其具有三种特征，方法一为标准RF-DNA法，只求方差、偏度、峰度，则特征具有3×3维，而方法二添加标准差这一特征，则特征具有3×4维。

每一架无人机的每一个跳频信号瞬时幅度、瞬时频率、瞬时相位特征所求标准差、方差、偏度、峰度的集如下：

Fa=[σσ2rk]a，

(15)

Fp=[σσ2rk]p，

(16)

Ff=[σσ2rk]f，

(17)

Fi=[FaFpFf] 。

(18)

式中：Fi为每一架无人机每一跳信号的特征集合。一架无人机所有跳频信号瞬态特征集如下：

FR=[F1,F2,F3,…,FN]。

(19)

式中：N为每一架无人机跳频信号总共个数。

所有无人机的无人机跳频信号瞬态特征集合表达式如下：

FC=[FR1,FR2,FR3,…,FRj] 。

(20)

式中：j为无人机个数。

取一组各个无人机瞬时幅度的标准差、方差、峰度、偏度特征进行特征统计，统计值如表1所示。

表1 遥控信号瞬时幅度统计特征表

2.2 识别算法

本文主要目的是从信号角度对无人机进行识别，其中识别的具体步骤如下：

Step1 采集无人机实测数据。

Step2 采用分形贝叶斯变点检测算法对无人机遥控信号瞬态部分进行提取。

Step3 采用RF-DNA统计特征法进行特征提取，提取采用两种方式，第一种含有标准差，第二种不含有标准差。

Step4 对Step 3所提取的特征集采用主成分分析(Principal Component Analysis，PCA)算法进行特征降维，特征降维可将维数降维为二维、三维、四维等，不同维数对识别率有一定影响。

Step5 通过SVM[13]分类器对降维后的数据进行分类识别。这里分类器采用Libsvm进行分类，该分类器具有多分类特点，采用的是一对一法完成多分类操作。

3 实验分析

本次实验主要采用自制硬件设备对大疆精灵4pro 1号及2号、司马航模x8hw、HM、大疆悟2、司马航模x25pro无人机信号进行采集，完成相应信号预处理及分类识别，采集系统如图2所示。

图2 无人机遥控信号采集系统实物图

通过对5架无人机共225组信号数据段进行实验，其中每个无人机训练数据30组，测试数据15组。

实验中，因含有三个瞬时特征且每一瞬时特征含有多种特征信息，且含有标准差的特征维数为12维，不含有标准差的为9维。采用PCA算法将特征集降维到二维、三维，其中二维散点图坐标轴F1、F2分别代表二维中维数特征，三维散点图中坐标轴F1、F2、F3分别代表三维中维数的特征。

实验1：采用不含有标准差、特征降维维数为二维的方式进行分类识别，实测数据二维散点图如图3所示。

图3 无人机遥控信号不含标准差二维特征散点图

该图共10类散点数据，主要是5类无人机训练数据和5类无人机测试数据，不同颜色及形状表示不同无人机。无人机训练数据用于建立数据单元库，无人机测试数据用于测试无人机识别率。从图中可知，不同无人机训练数据散点图分布区域不同，测试数据同样，但部分测试数据存在于其他组训练数据中，故该部分数据为错误识别组。无人机遥控信号不含标准差且二维特征识别率表如表2所示，其中无人机总识别率为80%。

表2 无人机遥控信号不含标准差二维特征识别率

实验2：采用不含标准差且特征维数为三维的方式进行分类识别，其散点图、识别率如图4及表3所示。

图4 无人机遥控信号不含标准差三维特征散点图

表3 无人机遥控信号不含标准差三维特征识别率

通过图4及表3可知，相对于二维而言，在同样不含有标准差时，三维识别效果更佳，识别率达到94.666%。

实验3：采用标准差且特征降维维数为二维的方式进行分类识别，其散点图及识别率如图5及表4所示。从图和表可知，相对于不含有标准差的二维散点图，含有标准差性能更好，且识别率达到97.333 %。

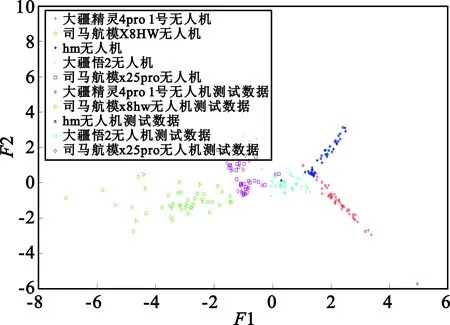
图5 无人机遥控信号含标准差二维特征散点图

表4 无人机遥控信号含标准差二维特征识别率

实验4：采用标准差，特征降维维数为三维方式进行分类识别，散点图及识别率如图6和表5所示，其中含有标准差且三维特征时，其识别率与二维特征相同。

图6 无人机遥控信号含标准差三维特征散点图

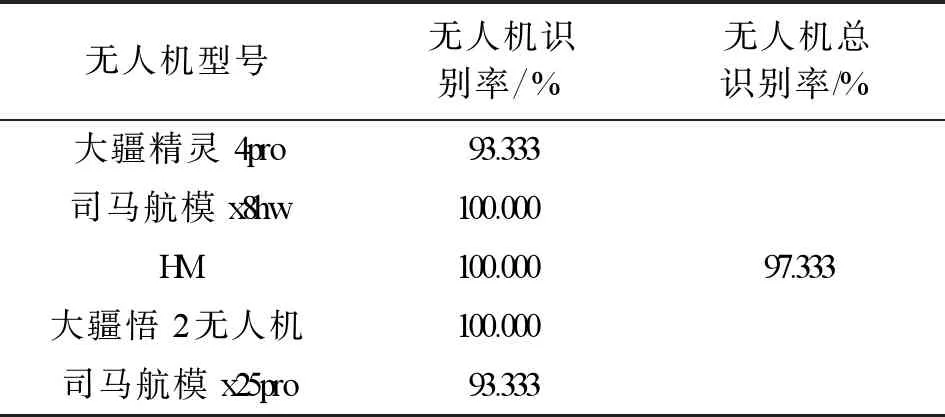
表5 无人机遥控信号含标准差三维特征识别率

为更进一步测试识别性能，在实测数据中叠加高斯白噪声，具体方法及步骤如下：

Step1 对实测训练数据建立数据单元库及训练数据特征集。

Step2 对实测测试数据叠加高斯白噪声。

Step3 通过分形贝叶斯变点检测、RF-DNA统计特征提取已加高斯白噪声后数据特征集。

Step4 Step 3中已加高斯白噪声后数据特征集与Step 1中训练数据特征集进行均值中心化，产生新特征集，取新特征集中已加高斯白噪声部分特征数据组作为测试特征集。

Step5 对Step 4所得测试特征集进行PCA降维，其中为验证维数影响，选择一维、二维、三维、四维作为测试变量。

Step6 采用SVM多分类器进行分类，绘出两种识别率曲线图，一种为含有标准差二维特征、含有标准差三维特征、不含有标准差二维特征、不含有标准差三维特征在不同信噪比下识别率对比图，命名为无人机遥控信号不同标准差及不同维数特征识别率图；另一种为含有标准差下一维、二维、三维、四维特征在不同信噪比的识别率对比图，命名为无人机遥控信号含有标准差下不同维数特征识别率图。

图7为无人机遥控信号不同标准差及不同维数特征识别率图。从图中可知，含有标准差识别率优于不含标准差识别率，且三维总体高于二维。含有标准差时，信噪比大于15 dB时，其二维及三维识别率大于70%，而不含有标准差时，信噪比大于20 dB时，其识别率大于70%。总体而言，随着高斯白噪声的增加，识别率逐渐下降，但因对其中心化处理、散点图较为集中等原因，其识别率在低于40%以下呈现低识别率随机起伏等混乱状态。

图7 无人机遥控信号不同标准差及不同维数特征识别率图

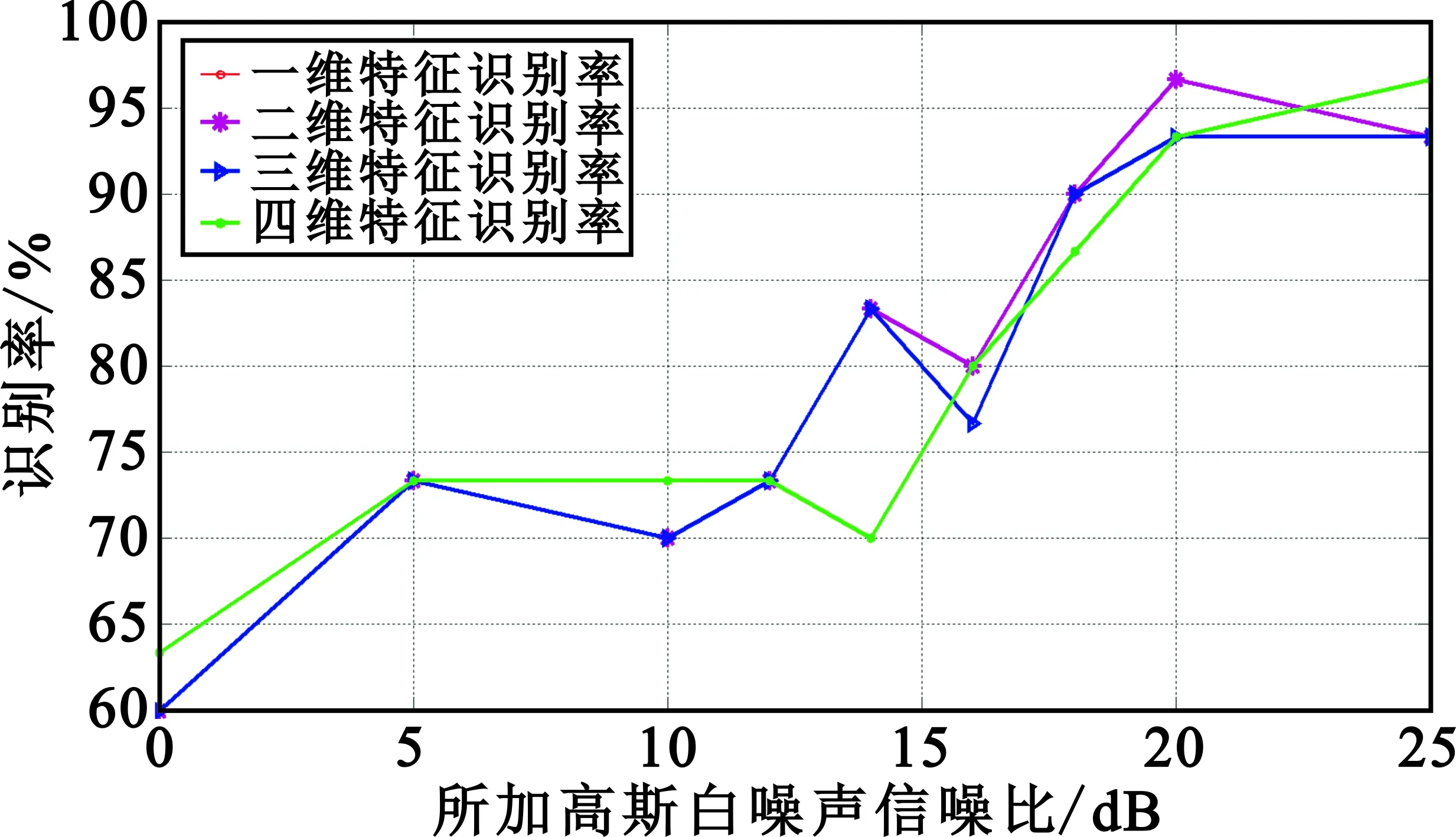
图8是在不同信噪比且含有标准差这一特征下不同维数识别率，总体来说，四维优于三维，三维优于二维及一维。在信噪比小于-5 dB时，各维识别率皆低于60%；在信噪比大于20 dB时，各维数识别率且大于90%，且四维最高。从识别曲线总体来看，维数越高其识别率更高。

图8 无人机遥控信号含有标准差下不同维数特征识别率图

通过以上四个实验得出采用RF-DNA法对实测无人机遥控信号可以完成其型号的区分，其中三维识别率最高，为97.33%。

为了更好地验证射频指纹方法的优点，取同一型号的两架大疆精灵4pro无人机进行个体区分实验，并得出散点图及不同维数识别曲线图。由图9(a)可知，同一型号无人机散点图较为紧密，区分难度较大，对分类器有一定要求。由图9(b)可知，一维与二维曲线相同，但整体维数对识别率无较大影响，主要受分析数量所限从而无法凸显维数优势。总体来说随着信噪比增加，识别率逐渐升高，当信噪比在17 dB以上时各维数识别率达到80%，因此可证明射频指纹识别法可对无人机个体进行区分。

(a)同一型号无人机遥控信号二维散点图

(b)同一型号无人机遥控信号含有标准差下不同维数特征识别率图图9 同一型号无人机遥控信号散点图及识别率图

4 结束语

本文针对无人机“黑飞”问题，采用RF-DNA方法完成了无人机具体型号及其个体的识别，可为无人机有效监管提供帮助。采用是否含有标准差以及不同维数作为测试条件，验证了在含有标准差且维数为四维时对无人机的型号区分效果最好。而通过对两架大疆精灵4pro无人机进行同一型号个体区分实验，得出RF-DNA能够区分同一型号无人机，但是无人机型号的区分抗噪性能高于同一型号的个体区分。此外，由于本实验目前只做了两架无人机的同一型号区分，后面应考虑增加更多同一型号无人机，以便于验证一定数量无人机同时存在对个体区别所带来的影响。并且，下一步应寻求更好的特征及分类方式从而更有效地对同一型号无人机进行个体区分，增加其实用价值。