基于支持向量回归的长期电路负载预测

2021-07-02张辉

电气传动自动化 2021年1期

张辉

（山西杏花村汾酒集团有限责任公司，山西吕梁032205）

长期预测的时间跨度是几周到几年之间。例如，电力系统的规划、新发电能力的建设计划和发电机组的购买，时间范围通常被设定为5年、10年、20年［1］。在这么长的规划期内，其实很难准确预测负荷需求，因为有很多影响负荷的因素通过直接或间接方式对基本预测过程产生影响。而且，所有的因素都是不确定和不可控的。因此，任何LTLF在本质上都是不准确的［2］。在过去的几十年中，许多方法被应用于提高LTLF的准确性。通常这些方法都不能处理负荷和影响负荷的因素之间的非线性或随机关系。

本文提出了针对我国境内五年负荷预测的SVR。并且，本文还加入了经济因素—GDP，而不是仅仅采用负荷的历史数据。值得注意的是，总负荷消耗量是衡量经济增长的关键指标，尤其是从全球经济衰退中复苏的指标。我们将重点放在负荷和GDP之间的关系上，并讨论这种关系对我国预期经济增长的影响，以提供建议。此外，它不需要收集大量的历史数据用于SVR的学习。因此，通过SVR，在数据有限的情况下，很容易实现LTLF。

1 支持向量回归

Vapnik提出的支持向量机（Support vector machines，SVMs）是克服上述ANNs缺点的重要发展之一。它不是通过实现经验风险最小化（ERM）原则以最小化训练误差，SVMs应用结构风险最小化（SRM）原则以最大限度地减少广义误差的上限。特别是随着Vapnik的ε－不敏感损失函数的引入，SVM也被扩展到解决非线性再回归估计问题，即所谓的支持向量回归（SVR）。

1．2 SVR 功能

其中，ɡ（x）表示数值预报结果，系数 w（w∈Rnh）和b（b∈R）是调整参数。

而式（1）中的参数向量w可以表示为:

1．3 经验风险的最小化

如上所述，SVM方法试图将经验风险最小化。

这里，Θε（yi，ɡ（xi））表示ε不敏感损失函数（图1当中较细的线）定义为:

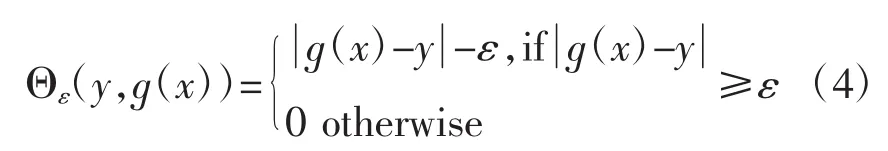
此外，Θε（y，ɡ（x））被用来寻找高维特征空间上的最佳超平面（图1（b）），以最大化将训练数据分成两个子集的距离。因此，SVR的重点是找到最佳超平面，并使输入数据与ε不敏感损失函数之间的训练误差最小化。

1．4 SVR 模型

SVR使整体误差最小化，因此。

其中，约束条件:

等式（5）中的第一项用于规范权重大小，惩罚大权重并保持回归函数平坦度。第二项通过使用ε不敏感损失函数惩罚了ɡ（x）和y的训练误差。C是权衡这两项的参数，高于ε的训练误差记为ξ＊i，低于 ε 的训练误差记为 ξi（图 1（b））。

1．5 核心函数

最后，在二元空间中得到SVR函数为（6）。

其中，K（xi，xj）称为核函数，而核值等于特征空间f（xi）和f（xj）中的两个向量xi和xj的内积，即K（xi，xj）＝f（xi）×f（xj）。有几种类型的内核函数。然而，到目前为止，很难确定特定数据模式的核函数类型。最常用的核函数是高斯径向基函数（RBF），其宽度如下:

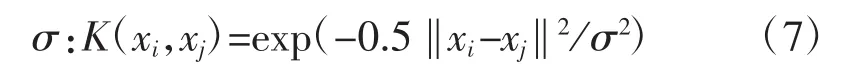
高斯RBF核不仅易于实现，而且能够将训练数据非线性地映射到一个无限维空间。因此，它适合于处理非线性关系问题。因此，本文指定了高斯RBF核函数用于研究。

图1 SVR过程

2 基于SVR的LTLF

在第二节中，我们建立了一种基于SVR的高斯RBF核函数的预测方法。在本节中，我们利用1995年至2016年的历史数据来学习SVR的参数，然后将SVR应用于我国境内5年的负荷预测。最后，根据“十三五”规划（2016－2020年）中提到的 6．5%的年GDP增长预期，对负荷产出、负荷进口和负荷出口进行了建议。尽管负荷输出的趋势与GDP相似，但GDP，负荷进口和负荷出口之间并没有平行关系。在本文中，负荷由公式（8）计算。因此，从1995年到2008年，GDP与负荷之间的关系是非线性的。

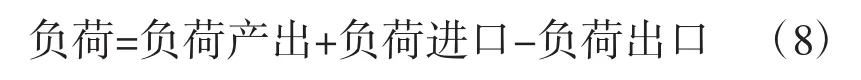
以上述历史数据为学习样本，我们实现了SVR的学习。我们将对2017年至2022年的负荷进行预测。根据“十三五”规划，2016年至2020年的GDP预期增长率为6．5%。因此，我们在本文中使用6．5%的比率。

3 建议

为了显示所提出的模型的优越性和推荐的可靠性，根据“十三五”（2016－2020 年）规划，我们还采用了其他的线性回归和反向神经网络（BPNN）作为比较。在“十三五”规划中，电力负荷的供应对经济活动的功能至关重要。在电力方面，由于电力基础设施建设需要3－4年的时间，应制定适当的电力供应建议和积极的策略，我国在缺电时期实行了“电力供应带动经济增长”的政策。