基于分布参数区间值比较的条件影响分析方法

刘 岑 吴森林 杨 帆 洪 凯 张 恕 刘小宁

(1.湖北轻工职业技术学院机电工程学院 湖北 武汉：430070；2.武汉软件工程职业学院机械工程学院 湖北 武汉：430205)

在工程实践中，分析物理量在一定条件下的分布规律与参数，是建立可靠性预测与分析方法的基础[1-6]；如何考虑加工处理方法或者使用环境不同即条件变化对于物理量分布规律与参数影响，是学术界与工程界值得研究的课题[7-10]。

基于数理统计与概率论的角度[11-12]，分析加工处理方法或者使用环境不同即条件变化对于物理量分布规律与参数的影响，实际是涉及两个随机变量分布规律确定与分布参数比较。对于基本符合正态分布的随机变量，均值、标准差与变异系数是描述其特征的分布参数，中心位置由均值描述，离散性由标准差描述，变异系数为标准差与均值之比，是衡量均值与标准差变异程度的一个统计量。当两个随机变量基本符合正态分布时，两个标准差的大小可采用F分布假设检验进行比较，两个均值的大小可采用t分布假设检验比较[10-15]；但是该方法似存在如下问题，两个标准差无显著差异是比较两个均值大小的前提条件，若两个标准差存在显著差异，无法比较两个均值的大小。

对于两个基本符合正态的随机变量，文中基于数理统计知识与概率论方法[11-12]，建立了比较其分布参数区间值受到条件变化影响的直接方法；根据有效样本，分析了分布参数区间值受条件变化的影响程度，为工程界确定加工处理方法或者选择合适的计算公式提供了依据。

1 基本理论与方法

1.1 构建随机变量的两种基本方法

在工程实践中往往会遇到两类问题，一是确定某个物理量的分布规律与参数，例如，在一定条件下，分析钢材屈服或抗拉强度分布规律与参数，或者是在条件改变时，分析钢材屈服强度与抗拉强度分布规律与参数的变化情况；二是比较设计公式的精度与稳定性[13-15]，例如，分析相同公式在不同应用范围精度与稳定性，或分析不同公式在相同应用范围精度与稳定性，或分析不同公式在不同应用范围的精度与稳定性。

为了解决上述两类问题，可采用两种方法构建随机变量：一是直接法，将某个物理量实际值作为随机变量，例如，在一定的条件下，将钢材屈服或抗拉强度实际值作为随机变量；二是比值法，将某个物理量实际值与公式计算值之比作为随机变量，例如，在一定的条件下，将承压设备的实际爆破压力与公式计算值之比作为随机变量。从数理统计角度，在一定的条件下，作为总体的某个物理量实际值的数量是无限的，虽然不可能通过试验测量物理量的所有实际值，但是可以将数量有限的有效实测值作为样本，通过样本统计分析随机变量的分布规律与参数。

假设RA与RB分别为A与B条件下符合正态分布规律的随机变量，其均值、标准差与变异系数分别为μA和μB、σA和σB与CA和CB，且其均值为正值。从工程实践的角度，RA与RB的分布规律与参数都是未知的，从数理统计知识与概率论方法角度，可以根据与随机变量RA和RB对应总体的有效样本，在一定显著度时采用假设检验的方法确定RA与RB分布规律，在一定置信度时通过似然分析得到分布参数的区间值。可分析条件变化对RA与RB分布参数的区间值或对公式精度与稳定性是否存在显著的影响。

1.2 两个随机变量分布参数的区间值

1.2.1 随机变量RA的分布参数

假设RAi(i=1，2，…，nA)是在A条件获得的nA组有效样本，其准确度与精密度分别为：

(1)

(2)

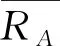
1)双侧置信度为(1-α)，均值μA的区间值为[11-12]：

μA∈[μAmin，μAmax]

(3)

其中

(4)

(5)

式中，μAmin与μAmax分别是单侧置信度为(1-0.5α)时RA均值μA的最小与最大值；tnA-1,1-0.5α为t分布系数，由自由度(nA-1)与单侧置信度(1-0.5α)查得。

文中取α=0.02[10]，所用t分布系数见表1[11-12]。

表1 分布系数

2)双侧置信度为(1-α)，标准差σA的区间值为[11-12]：

σA∈[σAmin，σAmax]

(6)

其中

(7)

取α=0.02[10]，文中所用的χ2分布系数见表1[11-12]。

3)双侧置信度为(1-α)，变异系数CA区间值为[11-12]：

CA∈[CAmin，CAmax]

(8)

其中

(9)

1.2.2 随机变量RB的分布参数

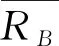
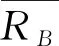
1)均值μB的区间值。双侧置信度为(1-α)时，在式(4)与式(5)中作变换A→B，可得到μB的区间值[11-12]：

μB∈[μBmin，μBmax]

(10)

2)标准差σB的区间值。双侧置信度为(1-α)时，在式(7)中作变换A→B，可得到σB的区间值[11-12]：

σB∈[σBmin，σBmax]

(11)

3)变异系数CB的区间值。双侧置信度为(1-α)时，在式(8)与式(9)中作变换A→B，可得到变异系数CB区间值[11-12]：

CB∈[CBmin，CBmax]

(12)

其中

(13)

1.3 随机变量RA与RB分布参数的比较

1.3.1 均值μA与μB比较

1)μA与μB有显著差异的判别。双侧置信度为(1-α)时，μA与μB存在显著差异是指μA与μB的区间值无共同部分，由式(3)与式(10)可比较μA与μB。

若满足

μAmin>μBmax

(14)

则μA与μB存在显著差异，且μA显著大于μB。

若满足

μAmax<μBmin

(15)

则μA与μB存在显著差异，且μA显著小于μB。

当均值满足式(14)或者式(15)时，可以认为条件变化是引起均值显著差异的重要因素。

2)μA与μB无显著差异的判别。双侧置信度为(1-α)时，μA与μB无显著差异是指μA与μB的区间值存在共同部分，由式(3)与式(10)可知：

若满足

μAmin<μBmin<μBmax<μAmax

(16)

表明μA的区间值全部包含μB的区间值，μA与μB无显著差异，但μA的波动范围比μB大。

若满足

μBmin<μAmin<μAmax<μBmax

(17)

表明μA的区间值被μB的区间值全部包含，μA与μB无显著差异，但μA的波动范围比μB小。

若满足

μAmin<μBmin<μAmax<μBmax

(18)

表明μA与μB的区间值部分共有，μA与μB无显著差异；但μA的下限比μB下限小，μA的上限比μB上限大。

若满足

μBmin<μAmin<μBmax<μAmax

(19)

表明μA与μB的区间值部分共有，μA与μB无显著差异；但μA的下限比μB下限大，μA的上限比μB上限大。

当均值满足式(16)～式(19)时，条件的变化对均值区间值影响不大。

1.3.2RA与RB标准差的比较

1)标准差σA与σB存在显著差异的判别。双侧置信度为(1-α)时，σA与σB有显著差异是指σA与σB的区间值无共同部分，由式(6)与式(11)可比较σA与σB。

若满足

σAmin>σBmax

(20)

则σA与σB存在显著差异，且σA显著大于σB。

若满足

σAmax<σBmin

(21)

则σA与σB存在显著差异，且σA显著小于σB。

当标准差满足式(20)与式(21)时，可以认为条件变化是引起其显著差异的重要因素。

2)标准差σA与σB无显著差异的判别。双侧置信度为(1-α)时，σA与σB无显著差异是指σA与σB的区间值存在共同部分，由式(6)与式(11)可知：

若满足

σAmin<σBmin<σBmax<σAmax

(22)

表明σA的区间值全部包含σB的区间值，σA与σB无显著差异，但σA的波动范围比σB大。

若满足

σBmin<σAmin<σAmax<σBmax

(23)

表明σA的区间值被σB的区间值全部包含，σA与σB无显著差异，但σA的波动范围比σB小。

若满足

σAmin<σBmin<σAmax<σBmax

(24)

表明σA与σB的区间值部分共有，σA与σB无显著差异；但σA的下限比σB下限小，σA的上限比σB上限大。

若满足

σBmin<σAmin<σBmax<σAmax

(25)

表明σA与σB的区间值部分共有，σA与σB无显著差异；但σA的下限比σB下限大，σA的上限比σB上限大。

当标准差满足式(22)～式(25)时，可认为条件的变化对标准差区间值的影响不大。

1.3.3RA与RB变异系数的比较

1)变异系数CA与CB存在显著差异的判别。双侧置信度为(1-α)，CA与CB区间值无共同部分表明他们存在显著差异，由式(9)与式(13)可比较CA与CB。

若满足

CAmin>CBmax

(26)

则CA与CB存在显著差异，且CA显著大于CB。

若满足

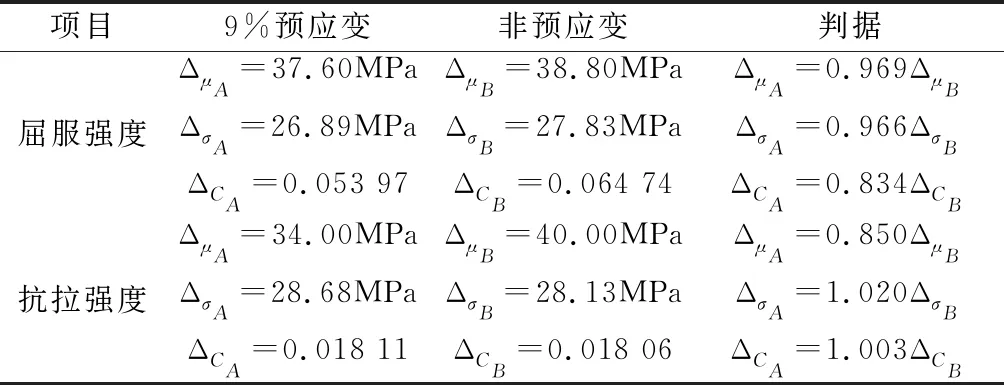
CAmax

(27)

则CA与CB存在显著差异，且CA显著小于CB。

当变异系数满足式(26)或者式(27)时，可以认为条件变化是引起变异系数显著差异的重要因素。

2)变异系数CA与CB无显著差异的判别。双侧置信度为(1-α)时，CA与CB无显著差异是指CA与CB的区间值存在共同部分，由式(9)与式(13)可知：

若满足

CAmin

(28)

表明CA的区间值全部包含CB的区间值，虽然CA与CB无显著差异，但CA的波动范围比CB大。

若满足

CBmin

(29)

表明CA的区间值被CB的区间值全部包含，CA与CB无显著差异，但CA的波动范围比CB小。

若满足

CAmin

(30)

表明CA与CB的区间值部分共有，CA与CB无显著差异；但CA的下限比CB下限小，CA的上限比CB上限大。

若满足

CBmin

(31)

表明CA与CB的区间值部分共有，CA与CB无显著差异；但CA的下限比CB下限大，CA的上限比CB上限大。

当变异系数满足式(28)～式(31)时，可认为条件的变化对变异系数区间值影响不大。

1.4 RA与RB分布系数的稳定性比较

双侧置信度为(1-α)时，分布参数稳定性是指波动范围的大小，波动范围小表明该分布参数稳定性好，否则，稳定性比较差。随机变量RA均值、标准差与变异系数的波动范围分别为：

ΔμA=μAmax-μAmin

(32)

ΔσA=σAmax-σAmin

(33)

ΔCA=CAmax-CAmin

(34)

在式(32)～式(34)中作变换A→B，可得到随机变量RB均值、标准差与变异系数的波动范围。

稳定性好与差可采用两种判据判别：一是绝对值比较，分别比较不同条件时均值、标准差与变异系数的波动范围，波动范围小表明对应参数的稳定性好。二是比值，分别比较不同条件时均值、标准差与变异系数的波动范围，比值小于“1”表明该分布参数稳定性变好，比值大于“1”表明该分布参数稳定性变差。建议以相对误差的绝对值5%为临界值，相对误差大于5%时，表明分布参数波动范围变化显著，稳定性发生显著变化；相对误差小于5%时，表明分布参数波动范围无显著变化，其稳定性也没有发生明显变化。

2 实例

2.1 实例1——分析加工方法的影响

2.1.1 基本情况与要求

工程上常用奥氏体不锈钢S30408制造深冷容器，深冷容器在室温制造，在液氮温度(-196℃)使用。为了保证深冷容器使用安全的同时提高钢材许用应力，在液氮温度(-196℃)时，有关文献[9]研究了9%预应变提高奥氏体不锈钢S30408屈服强度与抗拉强度可能性，文献[1，7-9]将9%预应变与非预应变的屈服强度或者抗拉强度视为随机变量，基于屈服强度与抗拉强度的有效样本，对其分布规律与分布参数进行了分析。

基本情况为：1)处于液氮温度(-196℃)的S30408钢，在9%预应变或者非预应变条件下，显著度为0.05时，屈服强度与抗拉强度都是基本符合正态分布的随机变量。2)经过9%预应变S30408钢，屈服强度的有效样本数为42，准确度与精密度分别为564.7MPa与49.72MPa；抗拉强度的有效样本数为43，准确度与精密度分别为1652MPa与53.49MPa。3)非预应变S30408钢，屈服强度的有效样本数为60，准确度与精密度分别为506.6MPa与62.50MPa；抗拉强度的有效样本数为60，准确度与精密度分别为1649MPa与64.52MPa。

要求评价9%预应变对S30408钢在液氮温度(-196℃)的屈服强度与抗拉强度影响，为选择或者确定材料的加工方法提供参考意见。

2.1.2 分布参数取值区间比较

将基本情况中的有关数据代入式(1)～式(13)，在单侧置信度为99%时，可得到屈服强度和抗拉强度分布参数的区间值，见表2；然后根据式(14)～式(31)得到分布参数的比较，一并列入表2。

由表2可知：1)与非预应变相比，9%预应变显著提高了S30408钢在液氮温度(-196℃)时屈服强度的均值，虽然标准差与变异系数无显著变化，但9%预应变仍然可降低标准差与变异系数；2)与非预应变相比，对于S30408钢在液氮温度(-196℃)时抗拉强度，虽然9%预应变并没有显著改变其均值、标准差与变异系数，但其均值得到一定提高，标准差与变异系数获得一定降低。3)由屈服强度分布参数取值区间可知，尽管当均值有显著差异时的标准差没有显著差异，但是变异系数也没有显著差异，这是分析中应该注意的。

表2 9%预应变与非预应变的分布参数区间值比较

2.1.3 分布参数的稳定性

将表2数据代入式(32)～式(34)，可得到屈服强度与抗拉强度分布参数稳定性的比较判据，见表3。

表3 9%预应变与非预应变时分布参数的波动范围比较

由表3可知：1)与非预应变相比，9%预应变降低了液氮温度屈服强度均值、标准差与变异系数的波动范围，三个分布参数的稳定性分别变好，其中变异系数波动范围降低5%以上，表明其稳定性得到了显著提高；2)与非预应变相比，9%预应变使液氮温度抗拉强度均值的波动范围降低5%以上，表明其稳定性得到显著提高，而标准差与变异系数的波动范围小于5%，表明这两个分布参数的稳定性没有明显变化。

2.1.4 评价

双侧置信度为98%时，对于液氮温度时的S30408钢，根据以上分析，1)9%预应变明显提高屈服强度均值，可在一定降低屈服强度的标准差与变异系数；2)经过9%预应变处理，屈服强度均值、标准差与变异系数的稳定性也得到改善；3)9%预应变在一定程度提高了抗拉强度的均值，降低了标准差与变异系数。因此，采用9%预应变是明显提高屈服强度均值的有效方法。

2.2 实例2——公式在不同应用对象的精度与稳定性

2.2.1 基本情况与要求

石油、化工、医药等行业常常采用单层圆筒容器作为承压设备，因为准确计算容器爆破压力是涉及安全的重要问题，我国采用标准规范容器的强度设计。对于实测爆破压力不超过105.5MPa的单层圆筒容器，标准规定采用中径公式计算其爆破压力[16]：

(35)

式中，u1为用中径公式(35)得到的圆筒容器爆破压力计算值，MPa；Rm为容器制造材料的抗拉强度，MPa；K为圆筒容器径比。

球形容器包括单层与多层结构，与圆筒形容器相比，球形容器具有受力均匀，承载能力高的特点，已在化工、石油、造船与能源等行业得到广泛应用。为确保其安全，我国采用标准采用中径公式的派生形式计算单层与多层球形容器的爆破压力[17-18]：

(36)

式中，u2为采用中径公式(36)得到的球形容器爆破压力计算值，MPa；Rmi为第i层球壳材料的抗拉强度，MPa；Ki为第i层球壳径比，Ki=Di+1/Di；Di、Di+1分别为第i层球壳内、外直径。

基本情况：将单层圆筒容器实际爆破压力与式(35)计算值之比视为随机变量，或将单层与多层球形容器实际爆破压力与式(36)计算值之比视为随机变量，基于有效样本的统计分析得到如下信息[18-19]：1)对于实测爆破压力不超过329.6MPa的单层圆筒容器，显著度为0.05时，随机变量基本符合正态分布；有效样本数为84，准确度与精密度分别为0.9859与0.04791。2)基于爆破压力不超过127.5MPa的单层与多层球形容器的实测数据，显著度为0.05时，随机变量基本符合正态分布；有效样本数为11，准确度与精密度分别为1.0255与0.02765。

要求评价式(35)与式(36)在应用范围分别为圆筒形容器与球形容器时的精度与稳定性。

2.2.2 分布参数取值区间比较

将基本情况中的有关数据代入式(1)～式(13)，在双侧置信度为98%时，可得到圆筒形容器与球形容器随机变量分布参数的区间值，见表4；然后根据式(14)～式(31)得到分布参数的比较，一并列入表4。

表4 不同应用对象中径公式分布参数区间值比较

由表4可知：式(36)在其应用范围相应随机变量的均值显著大于式(35)的，式(36)与式(35)相应随机变量的标准差与变异系数取值区间虽然分别有共同部分，即两个标准差与变异系数无显著差异，但式(36)的标准差与变异系数呈变小趋势。由表4还可知：虽然式(36)在其应用范围相应随机变量的均值显著大于式(35)的，且式(36)与式(35)的标准差无显著差异，但式(36)与式(35)的变异系数没有显著差异，这在分析中应该注意。

2.2.3 分布参数的稳定性

将表4数据代入式(32)～式(34)，可得到式(36)与式(35)在不同应用对象相应随机变量分布参数稳定性的比较判据，见表5。

表5 不同应用对象中径公式分布参数的波动范围比较

由表5可知：与式(36)相比，式(35)相应随机变量的均值、标准差与变异系数的波动范围明显变小5%以上，即式(35)在其应用范围的稳定性显著高于式(36)。

2.2.4 评价

双侧置信度为98%时，与应用范围为圆筒形容器实测爆破压力不超过329.6MPa的中径公式(36)相比，应用范围为球形容器实测爆破压力不超过127.5MPa的中径公式(36)，其精度略高于式(35)，但式(35)的稳定性显著高于式(36)。因此，将中径公式应用于球形容器强度设计时，我国采用专门标准[17]从设计、制造、检验等方面与其匹配。

3 结语

对于两个基本符合正态分布随机变量，应用数理统计理论与概率论知识，文中建立了比较其均值、标准差与变异系数关系的直接方法，可通过比较分布参数区间值和波动范围，评价加工或者使用条件变化对其是否存在显著影响；该方法具有直接和简便的特点，可为工程界确定材料加工处理方法或者选择合适的设计公式提供依据。双侧置信度为98%时，基于有效样本，分析了2个实例，得到如下结论。

(1)对于液氮温度时的奥氏体不锈钢S30408，可将实际屈服强度或者抗拉强度视为随机变量；9%预应变是著增提高其屈服强度均值的有效方法。

(2)与应用范围为实测爆破压力不超过329.6MPa圆筒形容器的中径公式相比，应用范围为实测爆破压力不超过127.5MPa球形容器的中径公式的精度略高，但稳定性显著降低。

(3)当条件变化时，不能从随机变量均值或者标准差是否存在显著改变定性判别变异系数的变化情况，这一点工程界必须给予足够重视。