地震共振涌浪作用下冰碛堰塞坝的漫顶溃决

2021-07-02姚令侃黄艺丹

西南交通大学学报 2021年3期

张聪，姚令侃 ,2,3，黄艺丹 ,2，苏玥

（1.西南交通大学土木工程学院，四川成都 610031；2.西南交通大学高速铁路线路工程教育部重点实验室，四川成都 610031；3.西南交通大学陆地交通地质灾害防治技术国家工程实验室，四川成都 610031）

堰塞湖广泛分布于我国境内且种类繁多，冰碛堰塞湖由于形成过程中坝体快速堆积，颗粒不均匀系数较大，随着气候变化与冰川活动极易溃决[1–3].在喜马拉雅山区特别是我国西南地区，冰碛湖数量庞大，近年来由冰碛湖溃决造成人员伤亡与财产损失的案例已有大量报道.例如在中尼公路贯穿的Bhotekoshi流域，自1980年以来爆发了6次冰湖溃决事件.其中发生于2016年7月5的贡巴通沙错冰碛湖溃决，引发泥石流灾害冲毁下游的Bhotekoshi水电站和中尼公路，造成约7000万美元经济损失.鉴于冰碛湖溃决危害之大，许多学者对其溃决机制进行了研究.Awal等[4]对有详细记载的20个冰碛湖溃决事件统计发现，仅有20%的冰碛湖溃决是由于坝内冰核融化或渗流导致的管涌破坏，而其余80%的溃决主要是涌浪漫顶诱发.通常，漫顶主要由冰川末端的冰舌崩落坠入湖中，激发涌浪引起.但2008年汶川大地震提供的资料显示，地震在都江堰市紫坪铺水库激发了巨大的涌浪，震后实地调查结合录像资料估算浪高超过3 m.虽然该量级的涌浪一般不会对人工大坝形成严重威胁，但对冰碛天然坝而言，完全可能达到决口溃坝的临界激发条件，可见地震激发涌浪漫顶是冰碛坝溃决的潜在诱因[5].

目前，对于地震涌浪的研究主要集中在地震力及产生的动水压力对大型人工坝体的破坏[6-8].对于地震涌浪的波浪效应研究则相对较少.Sato[9]通过线性简化方式将地震波谐波化，得出以地震涌浪浪高主要与水平地震峰值加速度（PGA，PPGA）、地震周期、坝前水深相关的结论.Demirel等[10]基于考虑水体压缩性的N-S方程建立地震涌浪数值模型，通过量纲分析建立以水深、最大地震动速度为自变量的波浪爬高公式.这些地震涌浪模型表明最大波高的影响因素主要有水深、地震周期与水平向地震峰值.以上研究[6-10]均针对大型水库，假设地震时坝体在半无限水体中水平往复运动产生涌浪.

根据物理学定义，当系统的自然频率与外界激励频率一致时，系统即可产生振幅较大的共振响应.地震时，当库湖水体自然频率与地震波频率一致时，即满足共振涌浪的激发条件.对大型水库而言，其自然频率极小，与地震波发生共振的机率也极小.然而小型库湖水体的自然频率一般较大，其自然频率可能处于地震波主要频谱区间内，相应地与地震波发生共振，形成较大涌浪的几率也较大.例如2010年4月4日墨西哥Ms7.2级地震时，监控拍摄了墨西卡利市游泳池地震涌浪的视频[11-12].视频中，虽然泳池水深仅约为1.8 m，但产生的涌浪波高却达到1.0 m 左右，按现行地震涌浪模型无法得到这样的涌浪高度.经分析，该泳池水体自然频率为0.17 Hz，与该场地震波的主频一致，因此推断，这是在共振状态下产生的现象.但是，小型库湖水体在地震作用下的共振是长久以来被忽略的问题.

当前，川藏铁路建设是我国的世纪性战略工程.帕隆藏布流域是川藏铁路必经的廊道，发育了我国罕有的海洋性山谷冰川类型，并由于海洋性冰川的活动形成了众多冰碛堰塞湖，冰碛湖溃决成为对川藏铁路线路方案起控制作用的重大灾害类型[13].冰碛堰塞湖一般属于小型天然湖泊，而该流域又处于高地震烈度区，因此地震共振涌浪作用下冰碛湖漫顶溃坝灾害机理已成为具有明确工程背景与科学意义的研究课题.

因此，本研究利用大型振动台造波实验模拟小型冰碛湖中的地震涌浪的共振现象，以获得地震共振涌浪运动规律及最大波高计算公式；依据粗颗粒泥沙启动水头条件与溃坝输沙临界水量条件建立涌浪作用下堰塞坝漫顶溃决判别的临界水文条件；最后根据此判据对帕隆藏布流域川藏铁路交通廊道沿线34个小型冰碛湖漫顶溃决危险性进行评估.

1 振动台实验

1.1 实验设备

本文利用大型振动台及水箱对地震涌浪进行模拟实验研究（图1）.水箱内安装4个波高仪，最高采集频率可达100 Hz，最大量程为1 m，采集精度为0.0001 mm.实验中，主要采用 1# 浪高仪记录的波高数据.水箱一端安装高清数码相机同步拍摄涌浪波动形态.

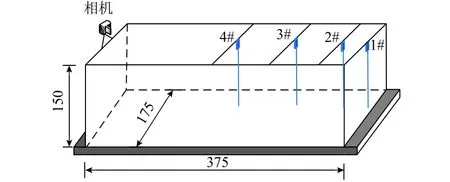
图1 实验装置（单位：cm）Fig.1 Sketch of the experimental setup (unit: cm)

本文的研究对象为小型堰塞湖中具有代表性的冰碛堰塞湖.中国西南高寒强震山区冰碛湖数量庞大，多位于冰川槽中，平面形态近似于矩形，因此采用矩形模型箱体.据统计[14]，该地区冰湖平均尺寸约为300 m.本文主要研究该区域尺寸约为100 m 的小型冰碛湖，因此原型与模型几何比尺约为25∶1.由于地震涌浪主要由惯性力与重力控制，因此，在满足几何相似基础上实验设计主要考虑弗劳德数相似.

1.2 实验设计

共振的激发条件要求系统自然频率与激励频率一致，因此实验前，首先需要获得水体系统的自然频率.矩形水体自然频率计算方法可参照线性势流理论[15]推导计算，如式（1）.

式中：fn为第n阶自然频率，n=1,2 , ···；kn=(2n+1)/L，L为激励方向水体尺寸；H为水深.

代入相应的尺寸参数，计算该矩形水体的自然频率为0.22 Hz.现通过振动台白噪声实验对该理论计算值进行校核.将幅值为0.10g持时为50 s的高斯白噪声作为激励信号输入振动台，根据所测得的涌浪时程曲线经快速傅立叶变换（FFT）得幅值谱，如图2，由图可知：自然频率为0.22 Hz.该数值与式（1）计算结果互相吻合，因此可用式（1）对近似矩形水体的自然频率进行估算.

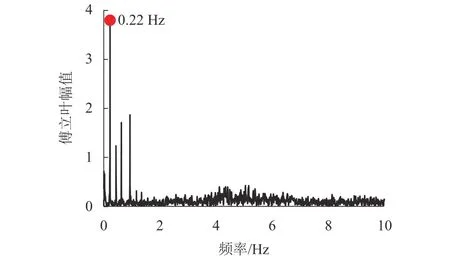
图2 白噪声激励下涌浪波高时程傅立叶幅值谱Fig.2 Fast Fourier transform (FFT) spectrum of wave height time history due to white noise excitation

获得水体自然频率后可进行地震波实验设计.地震波数据源于2013年芦山地震不同测站记录的两组主震地震动数据，编号为E1和E2.本文的实验方案设计为对比实验，其中E1地震波源自51LSF测站记录的地震波，主频为4.59 Hz（非共振实验），E2地震波源自53LDZ测站记录的地震波，主频为0.22 Hz（共振实验）.

由引言知，地震涌浪最大波高的影响因素主要有地震周期、地震波幅值与水深.考虑到地震波主频必须接近水体自然频率以满足共振条件，本文将地震波PGA与H作为共振条件下库水地震涌浪最大浪高的变量，进行单因素分析.实验按照水体深度20.0、25.0、30.0、35.0、40.0cm分为5组.每组实验施加的地震波PGA从0.05g增加至0.30g（每次增加0.05g）.实验共 60 小组.

2 实验数据分析与结论

2.1 非共振条件下地震涌浪特性分析

由于E1地震波主频不接近水体的低阶自然频率，在该地震波激励下水体不会出现共振现象.E1地震波及相应的波高时程曲线如图3所示.

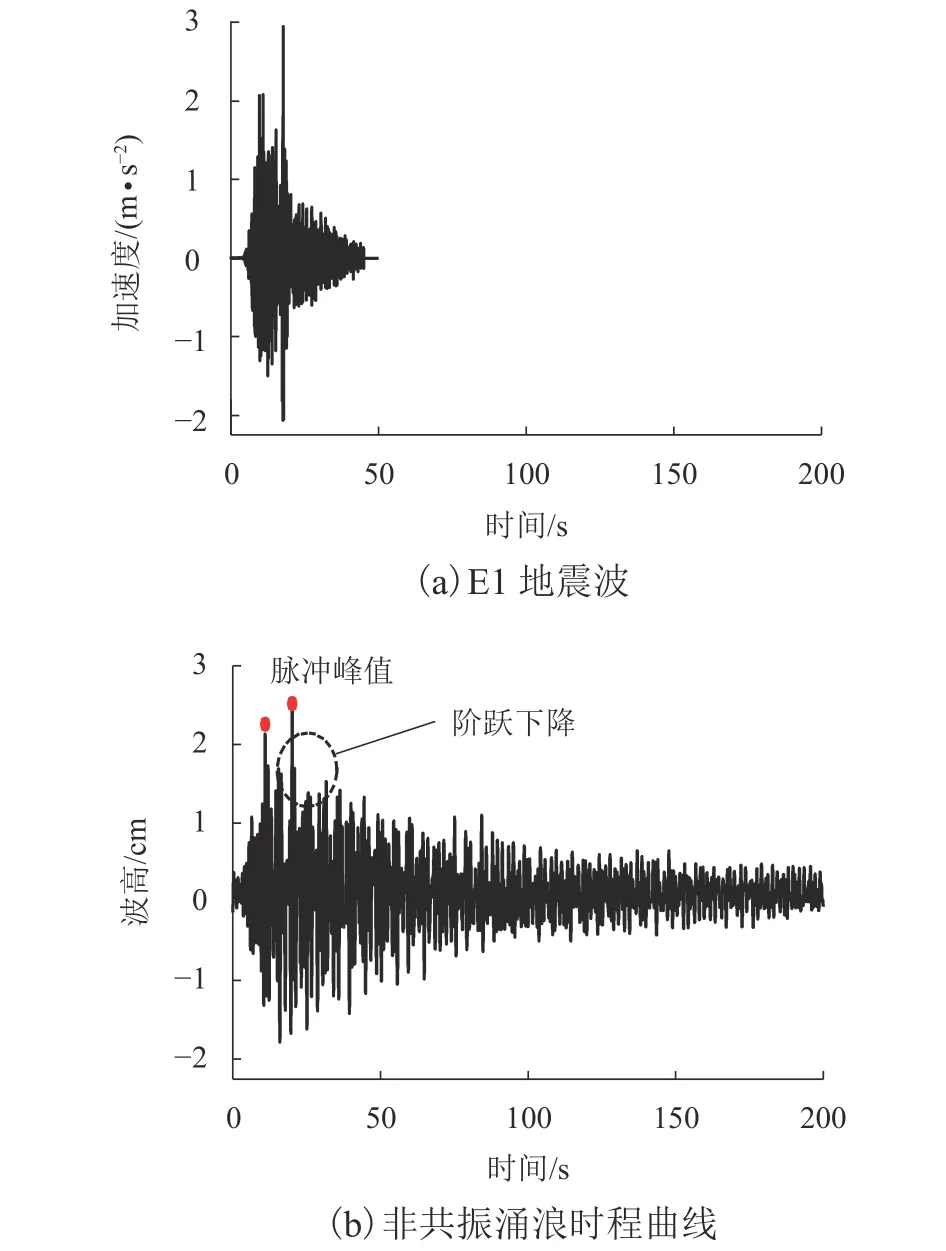
图3 E1地震波及相应的非共振涌浪时程曲线（水深 30.0 cm）Fig.3 E1 earthquake wave and the induced non-resonant water wave (water depth=30.0 cm)

在E1地震波作用期间水体的波高并不呈现明显共振放大趋势，且波浪运动幅度较小，波高峰值仅以数量极少的脉冲形式出现在地震强制激励期间.当地震波峰值过后，涌浪的波幅呈现“阶跃式”衰减.在时间轴上涌浪时程曲线呈现出与地震波较为明显的跟随状态.当地震激励停止后，涌浪进入自由波动段，涌浪幅度迅速衰减至初始状态.涌浪波高峰值快速衰减的主要原因是由于水体的低阶自然频率集中在小于1.00 Hz区间，而激励地震波则含有较多高频成分位于4.00～6.00 Hz.此时在水体强迫振动波浪频谱中，高频成分比较丰富.随着激励强度的减小，幅值较大的高频成分在水体阻尼作用下很快衰减，涌浪波高也随之迅速减小，此后涌浪则主要由幅值较小的低频成分组成.

2.2 共振条件下地震涌浪特性分析

E2地震波实验结果如图4所示.该地震波主频接近水体自然频率，依据共振的激发条件，箱体中形成了共振涌浪.对比图3（非共振）与图4（共振）发现，即使在地震激励PGA较小情况下，地震共振涌浪波幅也远超非共振涌浪波幅.图4中，在E2地震波激励下，涌浪波高迅速抬升，呈现出明显共振放大现象.随着地震作用达到峰值处，涌浪波高也接近峰值，此后虽然地震激励幅度减弱，但涌浪幅值并没有出现明显衰减，而是维持峰值波高直到地震作用结束.激励停止后，在水体整体运动的惯性作用下涌浪呈现出缓慢衰减状态.缓慢衰减的主要原因是共振涌浪具有较小的水体阻尼.图4（b）中，虚线方框段内水体波动的幅度差较小，涌浪维持较大幅值持续震荡，震荡周期数超过15次.在涌浪时程曲线上呈现出明显的稳态震荡阶段，在此期间涌浪起伏激烈，维持较大幅值形成持续性冲刷效应.

图4 E2 地震波及相应的共振涌浪时程曲线（水深 30 cm）Fig.4 E2 earthquake wave and the induced resonant water wave (water depth=30 cm)

2.3 共振条件下地震涌浪最大波高计算公式

由引言知，地震涌浪波高的最大影响因素主要有水深、水平地震幅值与地震主频.由于共振条件要求地震主频与水体自然频率接近，因此，本文将H与PPGA设为变量.对于E2地震波激励下的共振涌浪，首先设定模型箱水深为不同的数值，当地震波PGA从0.05g增加到0.30g时，地震涌浪最大波高值（h）如图5所示.由图可知：对于不同水深条件，共振涌浪的最大浪高均随PGA增加而近似呈线型增长趋势.同时，从纵轴方向可发现，对于一定的PGA值，当水深从20 cm增加到40 cm，涌浪的最大浪高均随H增加呈现单调增长趋势.因此，地震共振涌浪最大波高与水深和地震波PGA均呈现正相关关系.

因此地震共振涌浪最大波高的函数可设为h=f(PPGA,g,H).根据Bucking-ham定理进行无量纲化，得无量纲波高η=h/H，无量纲加速度a0=PPGA/g.由此可得无量纲化后的函数关系式 η=f(a0).对图5中实验数据进行拟合，得共振条件下地震涌浪最大浪高如式（2），拟合曲线如图6.

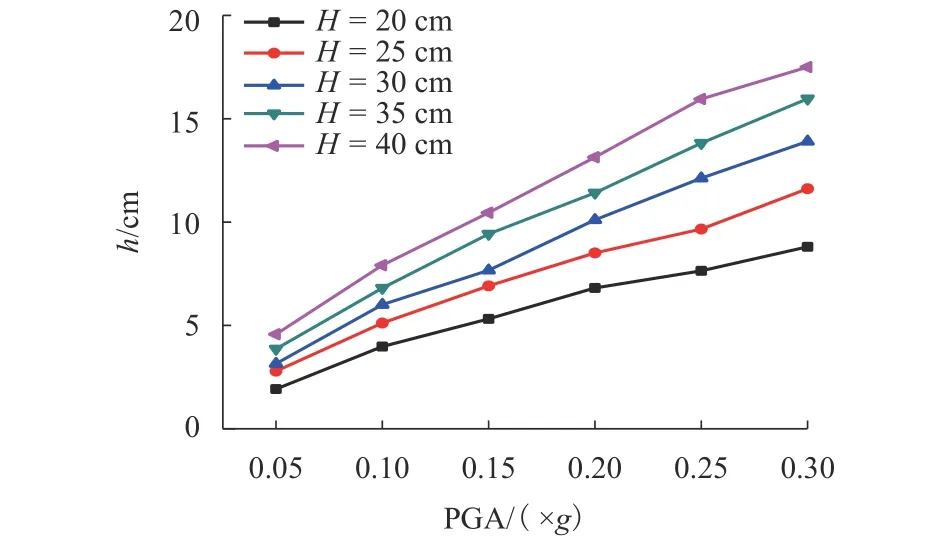
图5 不同水深条件下地震共振涌浪最大波高随PGA变化Fig.5 Variations of maximum wave elevation with increasing PGA at different water depths

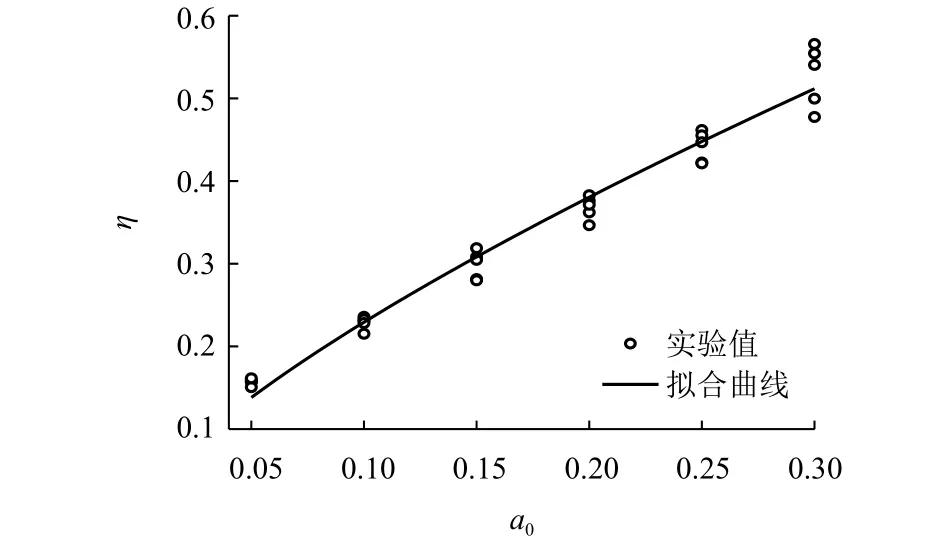
图6 无量纲最大波高拟合曲线Fig.6 Fitting curve for the non-dimensional maximum wave height

现采用引言中墨西卡利地震游泳池的案例对本文提出的式（2）进行验证.地震期间位于墨西卡利市消防站记录的南北向当地地震峰值加速度为0.264g，该地震波主频为0.17 Hz.震后调查显示该泳池南北向尺寸约为15 m，水深约为1.8 m，通过监控资料估算涌浪最大波高位于 0.70～1.00 m[12].通过式（1）计算该泳池水体自然频率为0.18 Hz，与该地震波主频（0.17 Hz）接近，由此可知泳池中的水体与地震波之间产生了共振.将相关参数代入式（2），得最大浪高为0.81 m，与视频估算的结果较为一致.值得注意的是，采用文献[11]中非共振条件下地震涌浪最大波高计算式计算该泳池的最大波高仅约为0.40 m，远小于实际数值.因此，式（2）可用于对共振条件下小型库湖的地震涌浪最大波高进行估算.

3 堰塞坝漫顶溃决条件及风险评估程序

3.1 临界波高与临界冲刷深度

第1阶段：涌浪掏槽，即涌浪翻越坝顶对坝顶与下游坝面溃口沟槽中的泥沙颗粒形成冲刷效应.该过程主要以下切侵蚀为主[16].溃口处泥沙的起动粒径与水流流速成正比.若流速较小，沟槽中大部分泥沙粗颗粒难以起动；在涌浪作用下，随着细颗粒被冲刷携带走，粗颗粒在沟槽底部表层形成抗冲粗化层从而保护沟槽不被进一步侵蚀.因此只有当涌浪的初始流速足够大，使得沟槽中的泥沙颗粒普遍启动无法形成抗冲粗化层时，才能形成波浪连续侵蚀作用.考虑以d95作为最大起动泥沙的代表粒径.因此相当于漫顶溃决第一个条件为：坝体沟槽中d95及以下粒径泥沙颗粒均要达到临界起动条件.蒋忠信等[17]依据该流速条件推导出冰碛坝漫顶溃决时溃口处临界水头高度估算式为（因流速与波高正相关）

式中：B为坝体宽；b为溃口沟槽平均宽度.

然而仅当波高大于H0时，坝体并不一定溃决.Balmforth等的水槽模型试验显示[16]，单一波浪通常无法造成土石坝体的漫顶溃决，必须在后续折返波浪的持续冲刷作用下坝体才能形成灾难性溃口.因此在涌浪导致堰塞坝漫顶溃决过程中必须考虑持时因素，即持续冲刷过程.

第2阶段：下切侵蚀至自发溃坝.当涌浪波高大于H0且存在连续波浪作用时，沟槽中大部分粗物质即可被波浪挟走无法形成粗化保护层.随着波浪持续冲刷沟槽到一定程度，波浪的作用减弱.此时溃口沟槽底部与静水面存在水头差，水流通过溃口外泄，当该水头差也大于H0时，即在水流持续不断的作用下，溃口底部泥沙均可持续地被水流挟走无法形成粗化保护层，下切侵蚀持续进行，溃决过程即可自发完成；此过程为波浪与水流的共同侵蚀，其中水流作用为主要作用因素.因此，H0也是坝体能够形成自发溃坝的溃口处临界冲刷深度.换言之，当涌浪冲刷沟槽深度到H0时，坝体在水流作用下即可自发溃决.

3.2 溃坝输沙临界水量条件

按3.1节中溃坝过程，若溃口沟槽达到临界冲刷深度形成自发溃决，则沟槽中单宽临界输沙体积Vs=H0L（L为坝体背水面沟槽长度），可现场实测或依据坝坡与水深的三角函数关系估算.崔鹏等[18]提出，当平均沟床比降超过50‰时，在沿程松散堆积物质丰富条件下，则会形成黏性泥石流.对应此条件，相应的沟谷泥石流含沙浓度可依据日本泥石流专家高桥堡推导的堆积层形成泥石流时，龙头达到稳定时的含沙浓度[19]为

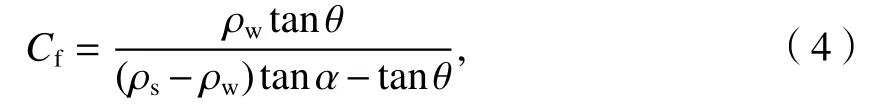
式中：ρs与ρw分别为固相与液相密度；θ为坡脚；tanα为拜格诺颗粒应力比.

一般情况下Cf取值区间为0.4～0.6.则冲刷单宽沟槽到H0所需水体体积为

式中：ρ0为坝体天然堆积体的密度.

涌浪在运动过程中，翻越冰碛坝体向下游传播，出水口处高度多与水面相平.每次的越坝水量的估算可采用孤立波波面方程计算涌浪在水平面以上的单宽水体体积估算[20-21]，则每次越坝单宽水量q0=因此可得溃坝所需最少冲刷波浪数（N为向上取整）为

根据3.1节粗颗粒起动条件与3.2节溃坝输沙临界水量条件，可得涌浪作用下堰塞坝漫顶溃决风险评估整体流程，如图7所示.水体自然频率f1的计算可采用本文推荐的式（1），h的估算可参考本文提供的式（2）.当场地资料难以获取时，对于小型冰碛堰塞湖统一按照共振工况考虑是一种偏安全的做法.

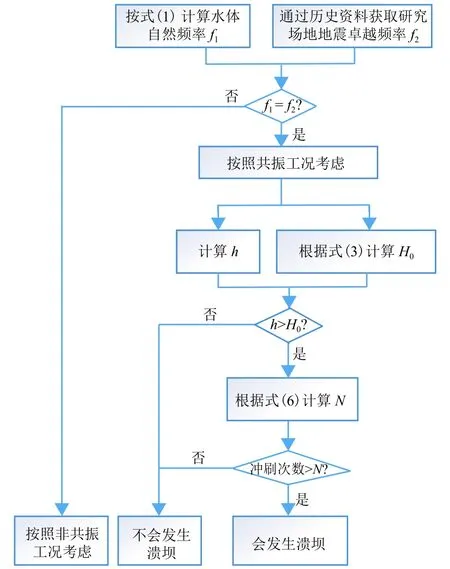
图7 涌浪作用下堰塞坝溃决风险评估程式Fig.7 Risk assessment procedure for the overtopping failure of natural dams due to earthquake-induced water waves

4 帕隆藏布流域冰碛湖漫顶溃决危险性评估

随着川藏铁路建设推进，帕隆藏布流域作为川藏铁路重要廊道，据2016年统计数据显示该流域分布大小冰湖130个[22]，且属于高烈度地震区.地震作用下冰碛湖溃坝灾害问题成为铁路选线设计阶段必须考虑的重要因素.当堰塞湖水体宽度小于100 m，水深低于20 m时，其自然频率一般处于0.10～1.00 Hz，而地震波的频谱通常宽于此范围，因此该尺寸范围的冰碛湖在地震时由于库水共振形成较大涌浪的可能性较大.根据第五代地震动参数区划图[23]，对该流域满足上述条件的小型冰碛堰塞湖进行漫顶溃决临界水文判定.首先按共振工况采用本文提供的式（2）计算地震共振涌浪的h，然后按照图7进行判别.对于共振涌浪峰值波高冲刷次数的计算，可依据当地地震部门的安评报告提供的地震波持时与共振涌浪周期比值进行估算.结合本文实验数据，在共振条件下，涌浪持续稳态冲刷次数可达到15次以上（图4）.按照此方法对34个小型冰碛湖进行风险评估.为形成对比，同时考虑共振与非共振两种工况下的冰碛坝漫顶溃决危险性，其中对于非共振条件下的涌浪最大波高的估算可依据文献[10-11]提供的公式进行估算，其漫顶溃决的判据采用传统的颗粒启动水头条件，而共振条件下的波高计算与溃坝条件采用本文提供的估算式与判据.依据现场调查资料取d95=15 cm[22].

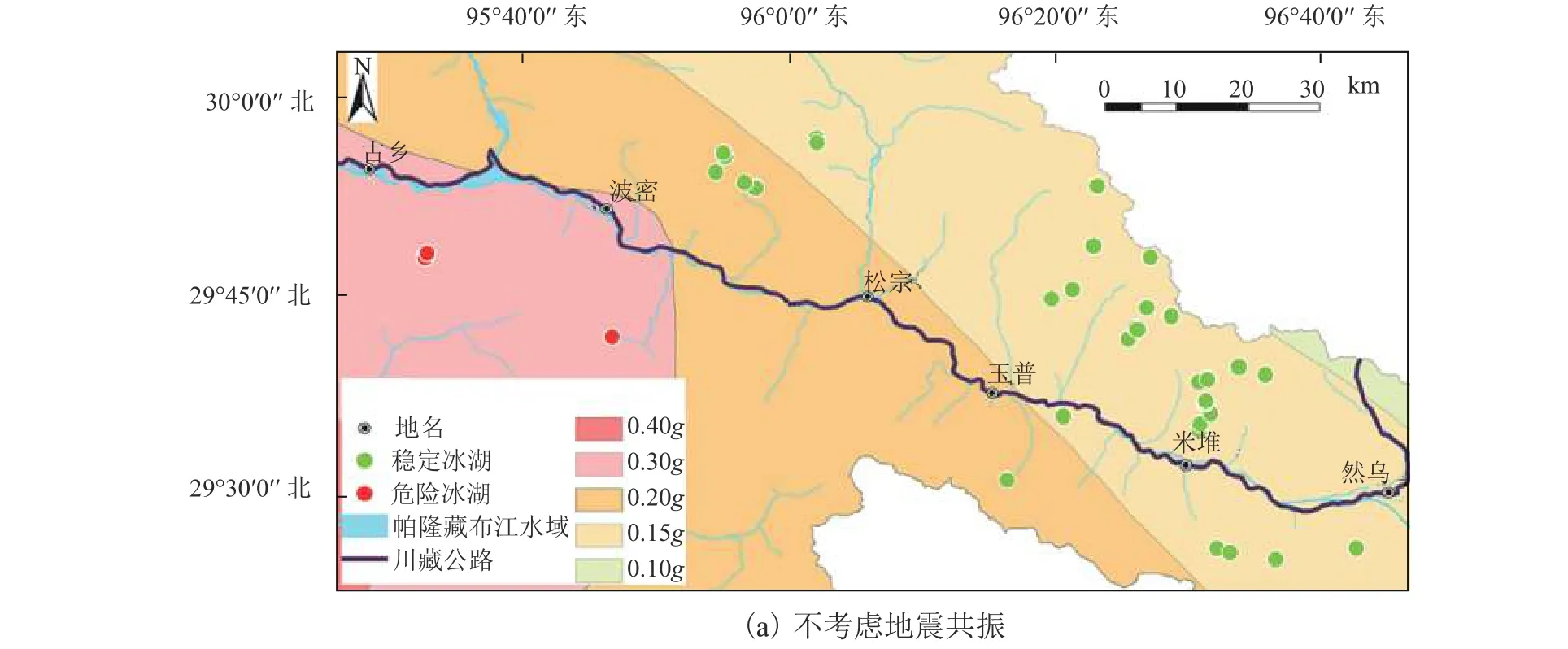
根据漫顶溃决危险性将该区域小型冰碛湖评估结果示于图8.可知，当不考虑小冰湖的地震共振可能性时，危险性冰碛湖仅分布于地震动PGA较大的0.30g区域.一旦考虑地震共振，危险冰碛湖不仅分布在0.30g区域，在PGA较小的 0.20g和0.15g的区域均有分布.该结论可为帕隆藏布流域川藏铁路选线设计以及为服役中川藏公路制定防灾减灾策略提供参考.