侧边加劲半圆形波纹钢板墙的抗侧性能
2021-07-02周林丽滕晓飞
周林丽 ,谭 平 ,滕晓飞
(1.广州大学广东省地震工程与应用技术重点实验室,广东 广州 510405;2.广州大学工程抗震减震与结构安全教育部重点实验室,广东 广州 510405)
剪力墙按材料分为钢筋混凝土剪力墙、型钢混凝土剪力墙、配筋砌块剪力墙和钢板剪力墙,其中以取材方便、工艺简单、整体性好且抗侧移能力较好的钢筋混凝土剪力墙的研究应用最为广泛成熟[1-2].混凝土剪力墙及砌块剪力墙通常因自重较大提高了框架梁柱的截面尺寸要求,且混凝土剪力墙及砌块剪力墙因耗能能力较差震后损坏严重给震后修复带来不便.钢板剪力墙作为一种新型抗侧力构件除具有较好的抗侧移能力外,相较于钢筋混凝土剪力墙其自重轻、震后易更换、且耗能能力强,这些特点使得钢板剪力墙在20世纪70年代便广泛应用于北美和日本高地震烈度区的多高层钢结构建筑中[3-4],其形式主要为平钢板剪力墙.平钢板因其平面外刚度小、受剪易屈曲及屈曲后结构的抗侧刚度急剧下降等因素给运输安装及结构的侧移控制带来诸多难题.
相对平钢板而言,波纹板的波形使钢板的面外刚度较大,其屈曲荷载也是同厚度平钢板的几倍至几十倍[5-6],将其作为抗侧力构件将会大大改善平钢板剪力墙极易发生弹性屈曲的不足,充分发挥钢板的延性及承载力.
目前波纹钢板在波纹腹板工形构件中的应用在国内外均已比较成熟,我国已将其纳入技术规程[7-8].而将波纹钢板应用于钢板剪力墙结构的研究起步较晚:Berman和Bruneau[4]首次对一斜向放置的梯形横截面波纹钢板墙进行了低周反复加载试验,试验结果表明,斜向波纹钢板墙的抗侧刚度及延性都得到了提高,其滞回环面积较大,但仍出现了较大的捏拢且滞回曲线并不对称的问题;Botros[9]采用有限元软件ADINA对横向梯形波纹钢板剪力墙及平钢板剪力墙进行了滞回分析,表明波纹钢板剪力墙比平钢板剪力墙具有更大的抗侧刚度、较高的承载力及更饱满的滞回环;兰银娟等[10-18]也先后对截面形式为梯形、波浪形、三角形、正弦波形及锯齿形的波纹钢板剪力墙进行了理论分析及试验研究,结果显示波纹钢板剪力墙在延性、初始刚度及耗能性能方面均比平钢板剪力墙有显著提高.但目前对于截面为半圆形的波纹板国内外并没有相关研究,半圆形波纹板因制作简单方便,可将其应用于钢板剪力墙结构.
本文由此提出一种新型侧边加劲半圆形波纹钢板剪力墙,为研究侧边加劲半圆形波纹钢板剪力墙能否实现“屈服先于屈曲”,首先建立了侧边加劲半圆形波纹钢板剪力墙的简化力学模型,根据力学模型推导了侧边加劲半圆形波纹钢板墙的弹性初始刚度及承载力公式;然后采用有限元分析软件ABAQUS对其进行弹性屈曲分析及非线性推覆分析,给出了侧边加劲半圆形波纹钢板剪力墙的弹性屈曲临界应力公式;并分析不同参数变化对波纹钢板剪力墙抗侧性能的影响及规律,为侧边加劲半圆形波纹钢板墙设计参数的选取提供意见和建议.
1 侧边加劲半圆形波纹钢板墙的构造
波纹钢板墙的截面形式有多种,本文突出分析半圆形的波纹钢板,其特点为:截面由若干个半圆组成;为便于门窗洞口的布置,与边缘框架的连接方式采用两边连接(即钢板仅与框架梁连接);波纹采用竖向设置,使波纹钢板可以抵抗竖向荷载的作用;波纹钢板左右两侧设置加劲肋以防止钢板侧边的局部屈曲,同时也为波纹钢板屈曲后形成的拉力带提供了一定的锚固作用,其结构形式和几何参数如图1所示.图1 中:b为波纹板板宽;h为板高;tw为板厚;d为圆形直径;r为波幅(圆形半径);q为波长;bf为肋宽;tf为肋厚.为表述方便,后文中将侧边加劲半圆形波纹钢板剪力墙统一简称为CSPSW.
由图1(a)可知:对于侧边加劲半圆形波纹钢板剪力墙,相较平钢板剪力墙,其截面设计参数仅增加一项r;相较其他截面形式的波纹钢板墙,其设计参数大大减少.侧边加劲半圆形波纹钢板墙的总体构造如图1(b)所示,波纹钢板墙通过鱼尾板采用高强螺栓(或焊接)与上下框架梁连接,侧边加劲不与框架梁连接.

图1 侧边加劲波纹钢板墙Fig.1 Schematic diagram of CSPSW
2 力学模型建立
2.1 简化力学模型
为研究侧边加劲半圆形波纹钢板墙的抗侧性能,假设与钢板墙相连的上下框架梁的刚度为无穷大,在水平荷载V作用下,侧边加劲半圆形波纹钢板墙可视为两端固定构件,其简化力学模型如图2(a)所示,在水平荷载V作用下的弯矩、剪力分布如图2(b)、图2(c)所示.
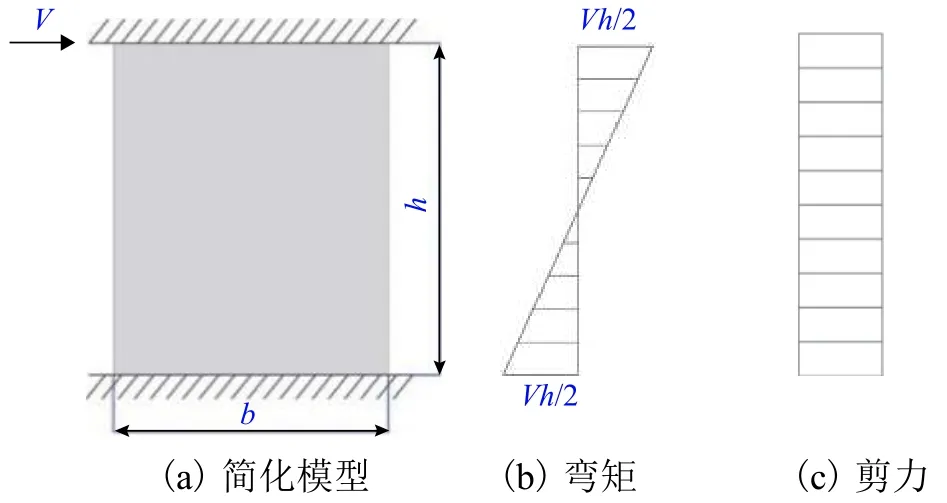
图2 波纹钢板墙简化力学模型Fig.2 Simplified mechanical model of CSPSW
根据文献[19]可知:钢板在水平荷载V作用下的总水平位移Δx由弯矩引起的位移ΔxM和剪力引起的位移ΔxV组成,即

经计算可得

式中:Es为钢材弹性模量,N/mm2;I为钢板截面惯性矩,mm4;Gs为钢材剪切模量,N/mm2;A为钢板截面面积,mm2;k为考虑剪应力在截面上分布不均的修正系数,对于薄壁环形截面,k=2.
2.2 弹性初始刚度理论公式
假设图2(a)中板宽为b的波纹钢板由2n个半圆形组成,则有2n×2r=b,A=πtwb,根据文献[20]波纹钢板墙的截面惯性矩为
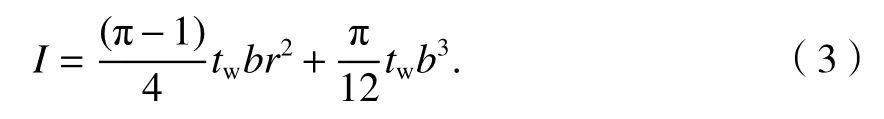
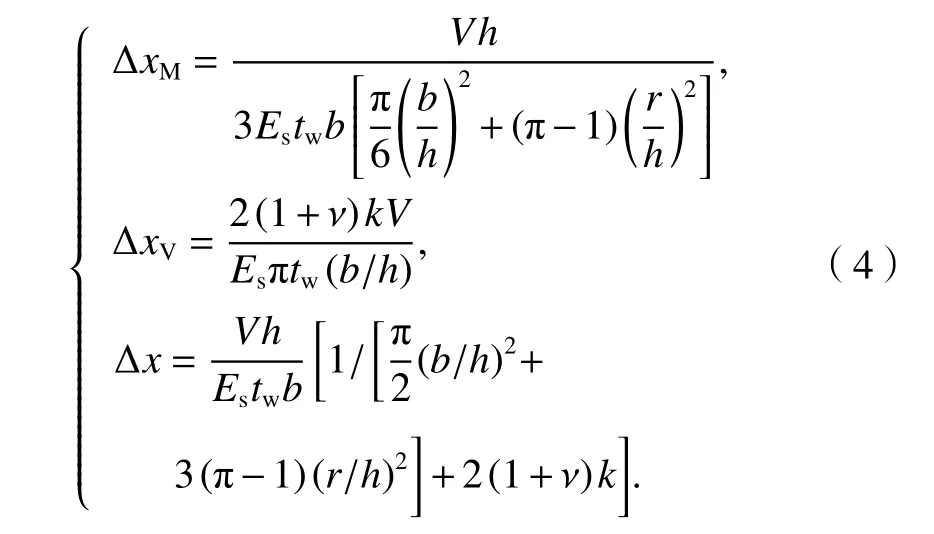
由V与Δx在弹性阶段的关系:V=K0Δx可得,侧边加劲半圆形波纹钢板剪力墙的弹性初始刚度K0为
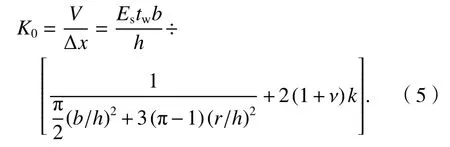
从式(4)可见,波纹钢板墙的剪切变形与圆形半径无关,在水平荷载作用下钢板墙的剪切变形与总变形之比为
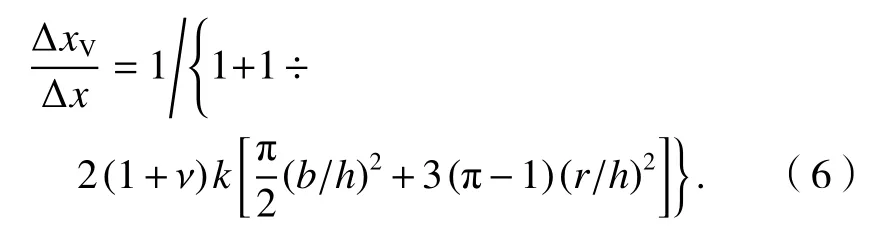
2.3 承载力理论公式
对于两边连接侧边加劲半圆形波纹钢板墙,其在水平荷载作用下上、下两边产生的弯矩M最大,如图2(b)所示,满足

而构件在弹性阶段的最大弯矩为

式中:We为钢板弹性抗弯截面模量;fy为钢材的屈服强度.
于是得到
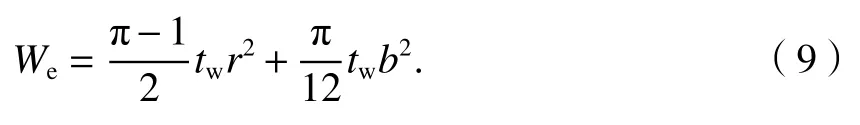
由式(7)、(8)、(9),可得侧边加劲半圆形波纹钢板墙的屈服荷载为
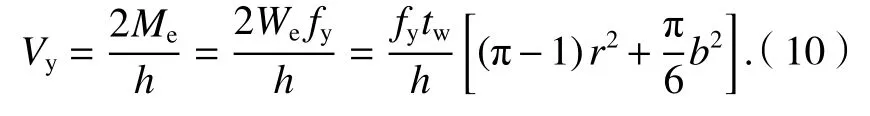
极限荷载为

式中:Mu为截面塑性弯矩;Wp为塑性抗弯截面模量,如式(12).
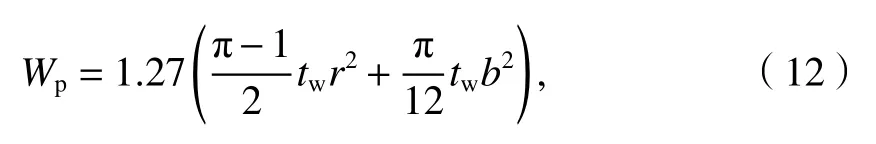
将Wp代入式(11)得到

2.4 弹性屈曲临界荷载
郭彦林等[18]以正弦波浪钢板为例,利用有限元软件对四边简支纯剪切作用下的波浪钢板墙进行弹性屈曲分析发现,在常用尺寸范围内,波浪钢板墙的屈曲模态为整体屈曲,根据有限元计算结果拟合得到整体屈曲下,四边简支波浪钢板墙弹性剪切屈曲临界应力为

式中:E为钢板的弹性模量;a为波浪形波纹钢板的波幅;ks为与边界条件有关的钢板受剪屈曲系数.
3 理论公式验证
3.1 有限元模型
利用ABAQUS对侧边加劲半圆形波纹钢板墙进行数值模拟,将波纹钢板与边缘框架组装并建立的单层波纹钢板有限元模型如图3所示,为研究侧边加劲半圆形波纹钢板剪力墙的主要设计参数(跨高比β=b/h、高厚比λ=h/tw、d、bf、tf)对半圆形波纹钢板剪力墙受力性能的影响,本文以不同b、tw、d、bf、tf参数建立了 19个不同几何参数的侧边加劲半圆形波纹钢板剪力墙模型,其中B-0为基本模型,其 模 型 参 数 为b=3000mm、h=3000mm、tw=3mm、d=60mm、bf=100mm、tf=10mm;在 其余参数不变的情况下,模型B-1、B-2仅改变模型B-0 的板宽,b分别取 1500 mm、6000 mm;模型B-3~B-6 仅改变模型 B-0 的板厚,tw分别取 4、5、6、9 mm;模型B-7~B-10仅改变模型B-0的直径,d分别取 30、80、90、120 mm;模型 B-11~B-14 仅改变模型 B-0 的肋宽,bf分别取 60、150、200、250 mm;模型B-15~B-18仅改变模型B-0的肋厚,tf分别取6、9、15、18 mm;模型 B-19~B-21 为作对比的平钢板剪力墙模型,d为0,b分别取 1500、3000、6000 mm.

图3 有限元模型Fig.3 Finite element model
3.2 材料模型和单元选取
模型中假设边缘梁、柱构件刚度无穷大,且两者铰接连接,以保证边缘构件不提供任何抗侧刚度,由波纹钢板承担全部剪力.为保证结构中波纹钢板墙先于主体结构屈服耗能,加劲肋及边缘梁、柱采用Q345级钢材,波纹钢板采用Q235级钢材,钢材的应力-应变关系采用理想弹塑性模型,对于梁柱材料Q345,屈服强度取 345 MPa;钢板材料 Q235,屈服强度取 235 MPa,弹性模量E=2.06 × 1011Pa,泊松比ν=0.3.模型采用壳单元S4R模拟加劲肋、边缘梁、柱及波纹钢板.
3.3 边界条件
根据实际工况,有限元模型采用如下边界条件:约束柱底节点所有平动及转动自由度,以模拟底部固接;为模拟上部楼板对梁的支撑作用,约束梁腹板及节点域所有节点的平面外自由度;采用Hinge连接单元模拟梁柱之间铰接;为保证梁与波纹钢板之间的荷载传递,波纹钢板上、下两端分别与附近的梁节点采用绑定约束.
3.4 理论公式验证
对图3中的有限元模型进行单调加载分析,为考虑结构的几何非线性,将弹性屈曲分析所得到的一阶屈曲模态的1%作为初始缺陷施加在有限元模型上.取位移-荷载关系曲线中的极值点作为极限荷载,采用通用屈服弯矩法确定屈服荷载,将由式(5)、(11)及式(13)计算得到的弹性初始刚度、屈服荷载及极限荷载理论解与数值解进行对比,对于平钢板墙不再适用,故平钢板墙仅给出数值解,结果见表1.

表1 理论公式的验证Tab.1 Verification of theoretical formulas
对于弹性初始刚度,理论解与数值解的最大误差为8.36%,此时对应于β=0.5.
由表1可知:当d>30mm时,侧边加劲半圆形波纹钢板墙屈曲荷载的理论解及数值解均高于屈服荷载,即侧边加劲半圆形波纹钢板墙在侧向荷载作用下先屈服后屈曲,表明半圆形波纹钢板墙防屈曲性能优越;而平钢板墙的屈曲荷载均远小于屈服荷载,表明平钢板墙在侧向荷载作用下先屈曲后屈服;平钢板墙的弹性初始刚度、屈服荷载及极限荷载均略大于半圆形波纹钢板墙,这主要是由于竖向放置的半圆形波纹钢板墙在侧向荷载作用下的“风琴效应”引起.
4 侧边加劲半圆形波纹钢板墙弹性屈曲
4.1 屈曲模态
对模型B-0~B-18施加单位水平荷载进行弹性屈曲分析,图4为参数变化时侧边加劲半圆形波纹钢板剪力墙的3种典型屈曲模态.
由图4可知:
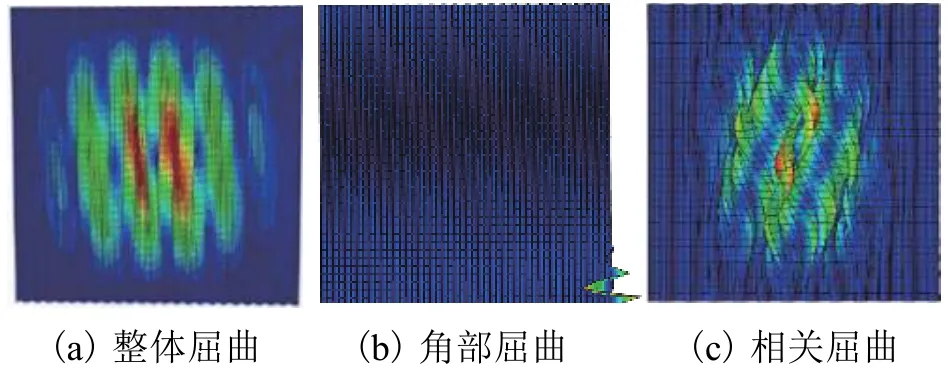
图4 侧边加劲波纹钢板墙的典型屈曲模态Fig.4 Typical buckling modes of CSPSW
1)在其他参数不变的情况下,随着β的增大,B-0~B-2均发生整体屈曲,且屈曲波均发生在钢板中心.
2)随着λ的降低屈曲波的数量逐渐减少,且当λ≥500时,B-0及B-3~B-5发生整体屈曲,λ<500时,B-6的加劲肋发生角部屈曲,这主要是由于当λ<500时,随着钢板板厚的增加,加劲肋的厚度比愈来愈小,加劲肋对钢板的约束不足,导致加劲肋先于钢板屈曲,因此对于两边连接侧边加劲半圆形波纹钢板墙,其加劲肋厚度比宜大于等于1.7.
3)改变波纹钢板墙的圆形直径d,B-0 及 B-7~B-9发生整体屈曲,且屈曲波的数量逐渐增多,B-10发生相关屈曲,为保证波纹钢板墙在侧向荷载作用下发生整体屈曲,其圆形直径应满足d<120mm.
4)按加劲肋厚度不宜小于剪力墙钢板厚度的要求,改变加劲肋宽厚比,在满足规范规定bf≤27tf的情况下[21],模型B-0及B-11~B-18均发生整体屈曲.
4.2 弹性屈曲临界荷载
根据式(14)上,通过有限元计算结果拟合得到侧边加劲半圆形波纹钢板剪力墙的弹性剪切屈曲临界应力如式(15),ks取值如式(16).


由弹性剪切屈曲临界应力值即可计算得到弹性剪切屈曲临界荷载Fcr为

由式(15)可看出,侧边加劲半圆形波纹钢板墙的弹性剪切屈曲荷载可视为平钢板墙弹性剪切屈曲荷载与波纹钢板墙几何形状带来剪切屈曲荷载增加的简单叠加,其中波纹钢板几何形状带来的弹性剪切屈曲临界应力的增加仅与钢板墙的幅高比r/h和厚高比tw/h有关,且当r=0时,此部分值为0,式(15)退化为两边连接平钢板剪力墙的弹性剪切屈曲荷载公式.
由式(15)计算得到的理论解与有限元模型得到的数值解对比结果如表1所示.理论解与数值解总体上吻合良好,模型B-9时的误差13.75%为最大误差,主要是由于圆弧直径d=90mm的侧边加劲半圆形波纹钢板墙的屈曲由整体屈曲向相关屈曲过渡,但此误差仍满足工程精度要求.
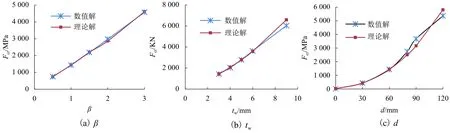
图5为不同参数下弹性屈曲临界荷载数值解的变化趋势,由图5可以看出:随着高厚比的减小、跨高比及圆形直径的增大,波纹钢板墙的弹性屈曲临界荷载呈线性增长,加劲肋肋宽从60 mm增至300 mm的变化过程中,其弹性屈曲荷载数值解与理论解的最大误差为2.5%;tf<3mm的情况下数值解与理论解差别很大,故在满足规范加劲肋厚度不宜小于剪力墙钢板厚度的规定下肋厚及肋宽对弹性屈曲临界荷载影响很小,可以忽略,也验证了式(15)中未考虑加劲肋肋宽的可行性;相较于图5(f)所示平钢板剪力墙B-19~B-21的弹性屈曲临界荷载,侧边加劲半圆形波纹钢板剪力墙的弹性屈曲临界荷载有显著提高.
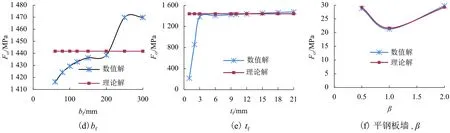
图5 侧边加劲波纹钢板墙弹性屈曲临界荷载数值解与理论解对比Fig.5 Numerical solution and theoretical solution comparison of elastic buckling critical load on CSPSW
5 侧边加劲半圆形波纹钢板墙破坏模式
由式(4)可知波纹钢板墙在单位侧向荷载作用下的弯曲变形、剪切变形主要与β及d相关,根据理论计算波纹钢板墙不同参数时的剪切变形所占比例及有限元数值模拟结果分析,侧边加劲半圆形波纹钢板墙的典型破坏模式有3种:
1)当β <1.0且3 0 mm≤d<90mm时,波纹钢板墙发生弯曲破坏,如图6(a)所示;
2)当β ≥1.0且3 0 mm≤d<90mm时,波纹钢板墙发生弯剪破坏,如图6(b)所示;
3)当β ≥1.0且d≥90mm或d<30mm时,波纹钢板墙破坏形式图6(c),与图6(d)所示平钢板墙破坏形式相似,这是由于此时波纹钢板墙发生局部屈曲,在侧向荷载下相邻波纹的面外变形逐渐合并形成了拉力带形式的褶皱.

图6 波纹钢板墙的典型破坏模式Fig.6 Typical failure modes of CSPSW
6 结 论
1)提出一种新型侧边加劲半圆形波纹钢板剪力墙,根据其简化力学模型推导了弹性初始抗侧刚度及承载力公式,并给出了弹性屈曲临界荷载计算公式,通过数值分析验证了理论公式的有效性.
2)波纹钢板墙在d<120mm及tf/tw≥1.7时,其屈曲模态均为整体屈曲;相同参数下,波纹钢板墙的弹性屈曲临界荷载及承载力均优于平钢板剪力墙;随着λ 的减小、β 及d的增大,波纹钢板墙的弹性屈曲临界荷载基本呈线性增长;参数bf及tf对波纹钢板墙弹性屈曲临界荷载的影响较小.
3)当d>30mm时,侧边加劲半圆形波纹钢板墙的屈曲荷载高于屈服荷载,即侧边加劲半圆形波纹钢板墙在侧向荷载作用下屈服先于屈曲,表明半圆形波纹钢板墙优越的防屈曲性能.
4)当β <1.0且3 0 mm≤d<90mm时,波纹钢板墙发生弯曲破坏;当β ≥1.0且3 0 mm≤d<90mm时,波纹钢板墙发生弯剪破坏;当β ≥1.0且d≥90mm或d<30mm时,波纹钢板墙的破坏形式为拉力带形式的“褶皱”.
致谢:广州市高校“羊城学者”首席科学家(12015 41630).
