地下水位变化对金州水准基岩标石的影响分析
2021-07-02尚贵佳李宝君于治信
尚贵佳,王 铁,李宝君,于治信
(金州地震台,辽宁 大连 116100)
0 引言
2018年11月1日金州水准新场地正式投入观测,一年多的观测成果显示,地下水位变化对水准观测存在一定的影响。然而水准路线的端点标石采用套管基岩标石,意在削弱地温、地下水和降水等干扰的不利影响。那么地下水对水准的干扰是由套管基岩标石的结构设计达不到排除地下水位变化影响要求造成的,还是施工质量问题?查阅有关资料发现,自上个世纪八十年代开始,地震系统台站水准路线的端点标石陆续采用套管基岩标石,通过近四十年的观测实践和研究,行业内一直认为,套管基岩标石在排除降水干扰上效果显著,地温干扰得到一定程度的减弱[1],但在地下水干扰方面,很多还没达到理想的效果,特别是地下水位变化幅度大时,表现的尤其明显[2]。具体表现为当地下水位迅速抬升时,水准观测高差滞后几天便大幅度畸变;当地下水位徐变时,水准观测高差与之产生相关变化。国内的学者和研究人员在这方面的探讨和研究并不多。
本文针对金州水准BM1、BM2测向高差,从地下应力变化的角度,利用有效应力原理对地下水位变化给水准高差造成的影响进行解释,推导出地下水位变化时,地下岩层有效应力变化量的计算公式,然后用地基沉降计算理论的“分层总和法”[3]对地下水干扰进行定量分析。
1 基本情况介绍
1.1 套管基岩标石结构及工作原理
套管基岩标石位于水准路线的两端,是水准路线高差测量的基准,其结构由里面的标杆管和外面的保护管组成(图1)。保护管要求钻探到完整基岩面下1m,并在此处变径,标杆管继续钻探到完整基岩面下3~5m。施工时用水泥砂浆回填,使保护管与钻孔孔壁固结为一体。标杆管底部与岩层之间用水泥砂浆灌注为一体,不能由此渗水、渗油,顶部焊接水准测量的铜标志。固定在标杆管上的滑轮扶正器既能扶正标杆管,又能使标杆管与保护管相对滑动[4]。
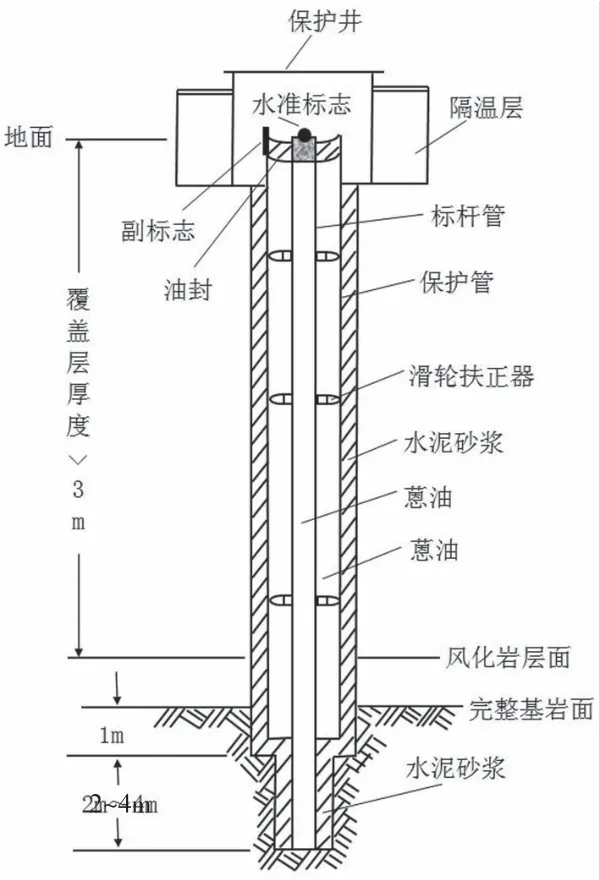
图1 套管基岩标石示意图Fig.1 Schematic diagram of casing bedrock marker
在保护管隔断覆盖层因降水、热应变等环境因素对标杆管干扰的情况下,标杆管下端与完整基岩相连,这样更能准确反映基岩层面的地应变变化。
1.2 BM1、BM2水准路线端点标石和地下水位观测井的有关情况
金州水准观测场地于2018年11月1日迁至金州地震台院内,BM1、BM2水准路线横跨金州断裂,套管基岩标石BM1位于断层上盘(西盘),岩性为震旦系甘井子组石灰岩,基岩完整,标石埋设深度为7.4m,覆盖层厚度2.5m;套管基岩标石BM2位于断层下盘(东盘),岩性为太古界鞍山群董家沟组黑云斜长片麻岩,基岩完整,标石埋设深度为9.1m,覆盖层厚度1.3m。地下水位观测井位于断层下盘,与套管基岩标石BM1的直线距离为61.5m,与套管基岩标石BM2的直线距离为23.2m,井深77.8m,井口高程与套管基岩标石BM1的测量标志基本一致,比套管基岩标石BM2的测量标志低4.4m。
2 地下水位变化引起套管基岩标石升降的物理解释
无论位于地表的覆盖土层,还是覆盖层以下的岩层,从物质状态来讲,一般都由三种物质组成,即固态物质颗粒、液态物质水和气态物质气体组成的混合体[5]。从各态物质的空间体积关系来说,岩土又由两部分组成:固体颗粒和孔隙部分。液态的水和气态的气体组成了岩土的孔隙部分,由于外部条件(如荷载作用)和内部条件(如渗流作用)容易引起其体积的变化,使岩体发生胀缩。而对于固体颗粒部分,通常认为是不可压缩的。因此,岩土的压缩就是其中液态的水从孔隙中被挤出,气态的气体被压缩和挤出的过程,相反岩土的膨胀也是侵入其中的水的张力和气体的膨胀所致。而岩土的胀缩必须在受到附加应力作用后才能发生,如建筑荷载变化在地基中引起的附加应力、地下水位变化引起的附加应力。岩土中应力除附加应力外,还包括自重应力,它是指岩土的自重引起的应力。自然界中的天然岩土层,形成至今已有很长的地质时间,在本身的自重作用下引起的土压缩变形早已完成,自重应力一般不会引起岩土层的胀缩,但是地下水位下降或上升会引起岩土层自重应力的变化,变化值即为附加应力,会引起岩土层胀缩。固定于基岩岩层上的套管基岩标石,必定随着基岩岩层的胀缩而升降,而地下水位变化引起的附加应力需要用有效应力原理来进行定性和定量分析。
3 利用有效应力原理分析附加应力变化
3.1 有效应力原理的适用性
饱和土是由土骨架和充满其间的孔隙水组成,当对土体施加外力后,一部分由土骨架承担,并通过土颗粒间的接触面传递,形成有效应力;另一部分由孔隙水承担,水不能承担剪应力,但可以承担和传递各向等压的应力,称为孔隙水压力。饱和土体上的总应力由土骨架承担的有效应力和孔隙水承担的孔隙水压力组成,而土的强度及变形都是由土的有效应力决定的。这就是饱和土体的有效应力原理[6],即:

式中,б为总应力;б′为有效应力;u为孔隙水压力。
根据许多岩石力学研究者的研究,只要岩石中有连接的孔隙(包括细微裂隙),对土力学中已经证明的太沙基有效应力定律,岩石中也是适用的[7];布雷斯(Brace)和拜而利(Dyerlee)根据大量的试验结果指出,土力学中的有效应力原理也适用于许多岩石[8]。所以地下水位无论在覆盖土层变化,还是在基岩层变化,都可以用有效应力原理来研究其对岩土层带来的竖向总应力和孔隙水压力的变化情况,进而求出有效应力的变化值,只要有有效应力变化值,就可应用弹性理论方法计算其所受压岩土层的变形量,这正是我们研究套管基岩标石底部基岩形变所需要的。
3.2 金州台地下水位变化引起的有效应力变化
分析
2019年金州台地下水位一直在基岩层内变化,其中2019年8月1日至8月13日,水位由7.490m骤升至10.458m,上升2.968m(图2)。根据有效应力原理,始水位与上升后末水位之间的岩体由不饱和变成饱和,孔隙水压力增大,相应的有效应力会发生变化,始水位以下岩体的有效应力也会发生改变,下面就先分析有效应力的变化情况。
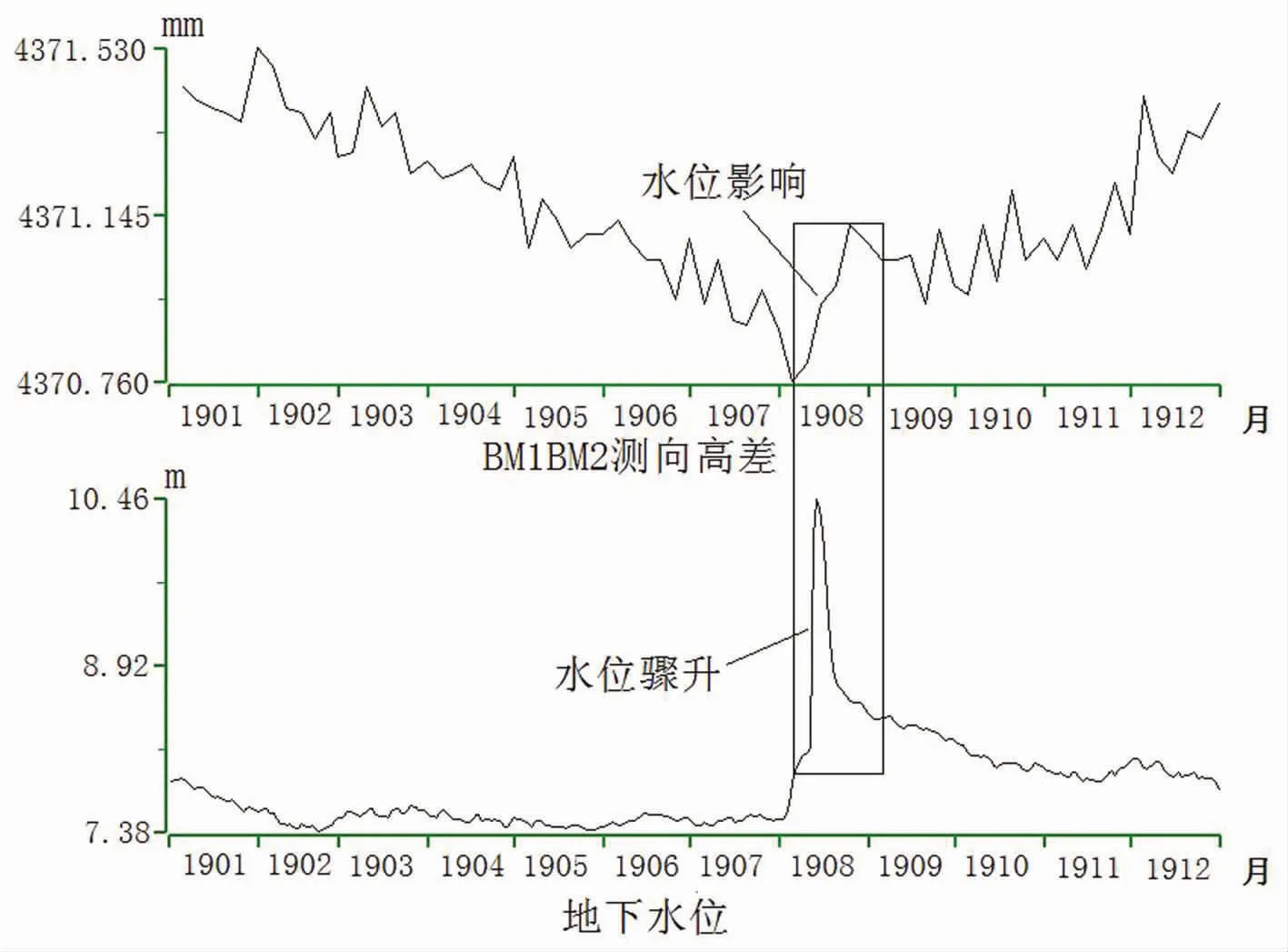
图2 台站水准和水位日均值对比图Fig.2 The daily mean comparison chart with station level and water level
这里不考虑岩体的胀缩过程,只考虑胀缩稳定后的岩层有效应力变化情况。把岩土层从地面到地下第一稳定不透水层分成四层(图3)。图3(a)为岩土层分层情况,其中r代表容重;图3(b)为水位上升前的竖向总应力分布情况;图3(c)为水位上升前的孔隙水压力分布情况;图3(d)为水位上升前的竖向有效应力分布情况,是由图3(b)的竖向总应力分布减去图3(c)的孔隙水压力分布所得;图3(e)为水位上升后的竖向总应力分布情况;图3(f)为水位上升后的孔隙水压力分布情况;图3(g)为水位上升后的竖向有效应力分布情况,是由图3(e)的竖向总应力分布减去图3(f)的孔隙水压力分布所得;图3(h)为水位变化前后的竖向有效应力变化量分布情况,由图3(g)的水位上升后的竖向有效应力分布减去图3(d)的水位上升前的竖向有效应力分布所得。
从图3(h)可以看出,从地面到末水位之间的岩土层,其有效应力没有变化;从末水位到始水位之间岩层的有效应力变化量为三角形分布,随深度增加呈直线减少;始水位至第一不透水层之间岩层的有效应力变化量为矩形分布,随深度增加保持不变;同时还能看出,有效应力变化量为负值,说明基岩岩层是被拉伸的。
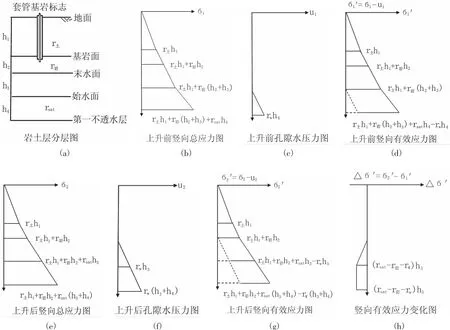
图3 应力变化分析图Fig.3 Stress change analysis chart
4 用分层总和法计算水位上升后套管基岩标石的竖向变形量
4.1 套管基岩标石的竖向变形量计算公式推导
分层总和法假设地基土是均匀、连续、各向同性的半无限空间弹性体,在侧向受限(只能发生竖向变形,而不能发生侧向胀缩)的情况下,将地基压缩范围内的土层分为若干薄层,采用胡克定律分别计算每一层的变形量,再计算各分层变形量总和。
根据分层总和法计算附加应力引起的胀缩,对于第i层的岩土微单元计算胀缩量的公式为:
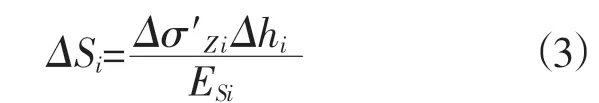
式中:ΔSi是第i层岩土微单元的胀缩量;Δσ′Z i是第i层岩土的附加应力,即有效应力增量;Δhi是第i层岩土微单元的厚度;ES i是第i层岩土的侧限压缩模量。
在地下水位上升时,根据分析所得的岩土层有效应力变化量的分布情况(图3(h)),岩土层发生的竖向变形量由两部分组成:
(1)始水位与升后末水位之间岩体的有效应力发生变化,附加应力呈三角形分布,把Δσ′Zi=(rsat-r岩-rw)hi代入(3)式,做积分则有:
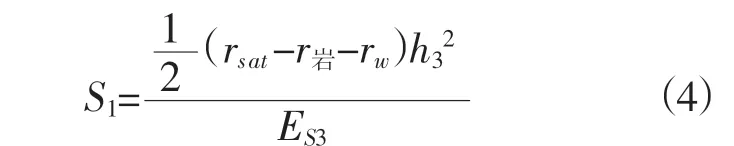
(2)始水位至第一不透水层之间岩体的有效应力变化量为定值,附加应力呈矩形分布,把Δσ′Z i=(rs a t-r岩-rw)h3代入(3)式,做积分则有:
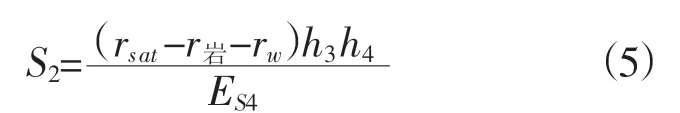
计算各层变形量总和:

4.2 压缩模量、饱和容重和计算深度的确定
压缩模量ES值计算采用下面公式[9]:
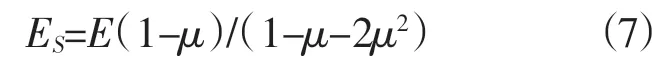
水侵入岩石后要大大降低杨氏模量(纵向弹性模量),在多孔岩石中尤为明显[8],有的可降到1/3。同时,岩石有裂隙、风化和破碎时,弹性模量也成倍降低[10]。考虑到基岩常年浸泡水中,并且水准场地建设报告中提到,三个套管基岩标石底部基岩呈中风化,所以石灰岩的E值取《工程地质手册》提供值(2.453×104~3.904×104MPa)下限的1/5,即E=4.906×103MPa;片麻岩的E值取《工程地质手册》提供值(1.432×104~55.621×104MPa)下限的1/5,即E=2.864×103MPa。中风化会使石灰岩和片麻岩的泊松比增大,但增大的数量级很小[10],而围压提高,泊松比会减小,所以泊松比直接取《工程地质手册》提供值的下限,石灰岩μ=0.18,片麻岩μ=0.20。
考虑基岩常年受到压缩,容重取《工程地质手册》提供值的上限,岩石的饱和容重按孔隙度计算,公式为:

公式(5)中的h4是始水位到地下第一不透水层的高差,而实际中,我们很难确定地下第一不透水层的位置,所以这里以金州77.8m深的地下水位观测井的井底为准,根据现场测量,h4=73.285m。
4.3 套管基岩标石变形量计算
具体各项参数值和计算结果见表1,可以看出套管基岩标石BM1抬升0.333mm,套管基岩标石BM2抬升0.686mm。

表1 标石底部基岩参数、有效应力变化量和变形量统计表
根据水准测量原理:h=a-b,地下水位变化后,标石BM1和标石BM2之间的高差为:
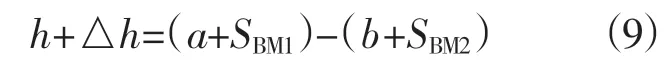
标石BM1和标石BM2之间高差的变化量为:
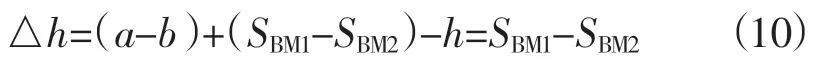
计算得到地下水位上升对标石BM1和标石BM2之间高差的影响值为0.353mm,从图2也能看出,此次地下水位变化的干扰影响后,BM1、BM2测向高差骤升0.36mm,理论计算和实际测量高差变化在数值和变化方向上是基本一致的。
5 BM1、BM2测向高差变化滞后于地下水位变化的解释
从时间上看,BM1、BM2测向高差受地下水影响变化滞后于地下水位变化5天左右,这从有效应力原理上也能解释得清。
当地下水位上升时,始水位与上升后末水位之间的不饱和岩体的孔隙并不能马上把空气排净充满水而立即变成饱和岩体,始水位以下饱和岩体也会随着孔隙水压力增大、有效应力减小而发生膨胀、稳定,这都需要有一个时间过程,所需的时间与岩体的渗透性、压缩性、孔隙比、排泄条件等有关,不同岩体所需的时间不同,少者几天,多者几十天;同样地下水位下降时,始水位与下降后末水位之间的饱和岩体变成不饱和岩体需要一个时间过程,下降后末水位以下的饱和岩体,也会随着孔隙水压力减小、有效应力增大而发生压缩、稳定,也需要一个时间过程。所以无论地下水位上升,还是下降,岩体的胀缩总是落后于地下水位变化。
6 结论
(1)金州水准套管基岩标石,仍受到监测场地周围地下水位变化的影响,这不是标石本身质量问题,而是标石底部的基岩层在地下水位变化的作用下而发生形变所致。
(2)地下水变化对套管基岩标石竖向形变影响量的大小,与水位变化幅度、水容重、基岩的压缩模量和孔隙度等相关。
(3)在钻套管基岩标石井孔时,准确记录岩层地质情况,留取岩芯做土工试验,取得压缩模量、孔隙度等地质参数,以备建立数学模型,从观测数据中排除地下水干扰。
