基于振动监测的混凝土重力坝模态识别结果的评价研究
2021-07-02毛昊然陈诗怡袁兴国
毛昊然,程 琳*,陈诗怡,杨 杰,袁兴国
(1.西安理工大学 西北旱区生态水利工程国家重点实验室培育基地,陕西 西安 710048;2.华能澜沧江新能源有限公司,云南 昆明 650214)
0 引言
我国处于环太平洋地震带与欧亚地震带之间,很多大型水利工程都位于强震区,地震频发。例如,位于滇西北川西南活动构造区的龙开口重力坝曾受过Ⅷ度地震影响[1];鲜水河—滇东地震带的金沙江鲁地拉重力坝多次发生7级以上的地震,最高震级为8级[2]。混凝土重力坝是水利工程常用的坝型之一,国内外对混凝土重力坝遭遇地震而发生损伤破坏的案例也多有报道。在国外,印度的Koyna重力坝1967年经历了6.5级水库诱发地震,下游折坡点高程附近的上、下游坝面出现大量水平裂缝,并有贯穿性裂缝[3];英国的Blackbrood重力坝1957年经受了6.4级地震,大坝下游面出现裂缝[4]。在国内,2013年四川芦山地震,震中附近的胜利电站混凝土重力坝左岸岩石松动,坝体内部严重渗漏;宝兴水库混凝土坝下游右坝尖发生山体滑坡,严重影响了大坝安全运行[5]。通过系统识别(主要是模态识别)来获得表征结构动力特性的模态参数,以分析地震前后混凝土重力坝结构动力特性的变化情况,以便进行结构的震损评估、模型修正和抗震分析是保障强震区混凝土重力坝结构安全、指导大坝运行管理和修复、提高大坝抗震性能等均具有重大意义。在各种模态识别方式中,利用振动观测系统采集的大坝结构在地震和环境激励下的原型振动观测数据,来识别混凝土重力坝结构的模态参数,无需进行额外人工激励,节约大量成本,符合大坝实际运行工况以及边界条件,可以获得真实反映结构工作状态下动力特性的特征参数[6]。
1962年,我国在新丰江大坝上布设了第一个强震观测台[7]。陈厚群[8]院士精选收录了我国1966—1995年间758条水工建筑物强震记录中的299条重要强震记录,并出版书籍供科研工作者查阅和研究。张立飞等[9]人基于强震观测数据对龙羊峡拱坝进行了模态分析,并与以往的模型试验、理论计算进行对比,发现对原型强震记录进行分析得到的模态参数更符合大坝实际动力参数。徐辰奎[10]以水口重力坝地震中的原型观测数据作为依据,采用功率谱峰值法、随机减量和时域ITD法、有限单元法对其自振特性进行研究。程琳等[11]提出了基于Hankel矩阵联合近似对角化的运行模态识别方法,并根据地震观测记录对某重力坝的模态参数进行了识别。在国外,韩国水资源公司(K-Water)在2006年开发了一套大坝地震观测系统,用于监测坝体的环境振动和地震[12]。Alves等[13]采用分段方式基于程序MODE-ID对美国某拱坝1994年的Northridge和2001年的San Fernando的地震记录进行了分析。混凝土重力坝作为一种自由度高的超静定水工建筑物,模态密集,受工作环境影响严重,使得对结构的模态分析较为复杂。就地震观测的系统识别而言,由于地震性质复杂,其存在的优势和劣势频率成分给结构模态参数识别带来困难。而环境振动监测数据主要用于房屋、桥梁等建筑的模态识别,在坝水体系中的应用还较少。且因为环境振动振幅较小,易受噪声影响,使模态分析时虚假模态剔除和系统定阶有很大的困难。
本文介绍了四种常用模态识别方法的基本理论,并以水口重力坝为例,利用不同方法对大坝地震观测数据和环境振动观测数据进行模态识别。通过识别结果的相互比较,分析基于地震观测或是环境振动观测进行模态识别的优劣性。
1 基于振动观测结构系统识别方法
基于原型观测的结构模态识别方法可以分成考虑输入和输出的(IO)方法和仅考虑输出的(OO)方法。在各类模态识别方法中,自回归各态历经(ARX)模型、频域分解(FDD)、特征系统实现算法(ERA)和随机子空间识别(SSI)最为常用。其中ARX模型是一种IO类的方法,FDD是一种OO类的方法,而ERA和SSI都有IO和OO两个不同的版本。以下对这四种识别方法的基本原理进行了介绍。
1.1 ARX模型
ARX模型可用下式表示:
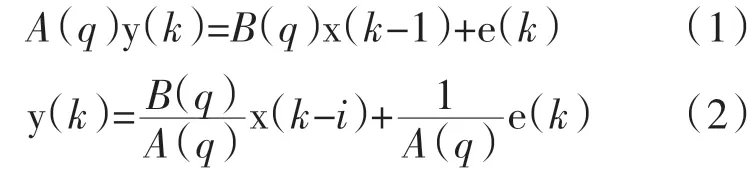
式中,x(k-1)为输入向量;y(k)为输出向量;e(k)为误差。A(q)、B(q)是关于q的多项式。
解A(q)=0的根后,即可求出各阶振型频率fk以及阻尼比ξk:
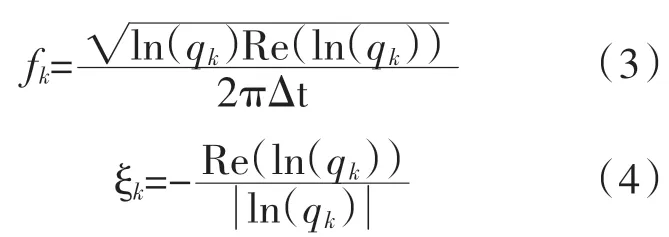
其中,qk是A(q)的特征值;Re(*)是*的实部。
1.2 FDD
FDD由峰值拾取法(PP)发展而来,在使用中,仅需拾取峰值即可。它的优点是不会产生虚假模态。FDD法假设系统受到白噪声激励,输出响应信号功率谱密度函数为:
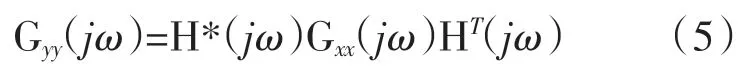
式中,Gxx(jω)是输入信号的功率谱密度矩阵;Gyy(jω)是输出信号的功率谱矩阵;H(jω)是频响函数矩阵;上标*表示伴随矩阵,上标T表示转置矩阵。
方程(5)可转化为:
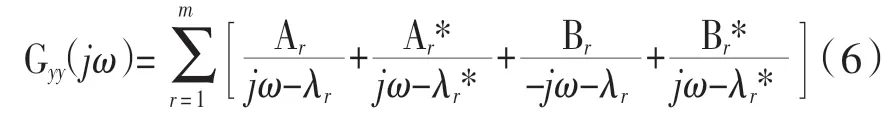
Ar是所得假定频响函数矩阵;Br是假定频响矩阵;λr和λr*分别是系统极点和伴随矩阵的系统极点。
根据各通道测量的响应信号,计算相应的功率谱密度矩阵,然后进行奇异值分解。
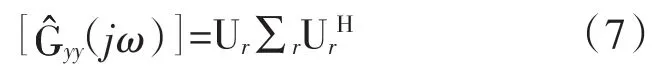
利用Ur即可得到模态振型的估计值。
1.3 ERA
考虑噪声的输入输出离散状态空间模型可用下式表示:
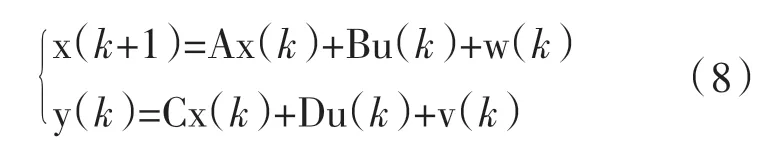
A、B、C、D分别为状态矩阵、输入矩阵、输出矩阵、传递矩阵,x(k)为状态向量,y(k)为输出数据,u(k)为输入数据,w(k)、v(k)为白噪声。
不考虑输入,仅考虑输出信号时,离散状态空间模型可以改写为:
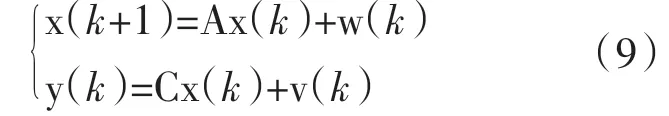
ERA-IO利用Kalman滤波器(OKID)方法计算得到脉冲响应函数h(k),构造Hankel矩阵:

对H(k-1)进行奇异值分解后,通过一系列处理和变换,可以获得对A、B、C、D的合理估计,便是系统的最小实现,以此为基础可以进一步得到结构的模态参数。OKID方法具体介绍以及模态参数的算法可参考文献[14]。
ERA-OO是利用自然激励技术(NExT)得到环境振动激励下结构响应的互相关函数来代替结构的脉冲响应函数,再进行类似步骤得到结构模态参数[15]。
1.4 SSI
SSI-IO算法是根据输入输出离散状态空间模型(8),将输入输出数据组成Hankel矩阵,计算矩阵的行空间投影,并对投影进行奇异值分解,得到可观测矩阵和状态序列的卡尔曼滤波估计,进而确定系统矩阵A、B、C、D。该方法的具体介绍见参考文献[16]。SSI-OO算法,由仅考虑输出的离散状态空间模型(9),定义输出协方差矩阵为数学期望。
构造托普利兹矩阵如下:
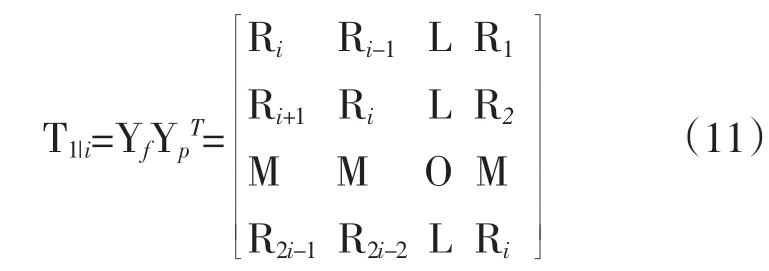
将矩阵T1|i分解为T1|i=OiTi,其中Oi为可观测矩阵,Ti为扩展可控矩阵,对其进行奇异值分解得:
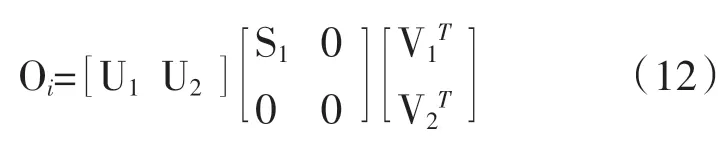
根据不为0的奇异值个数确定系统阶次,再根据U1、S1计算出系统矩阵、输出矩阵,最终得出系统的模态参数,该方法的具体介绍见参考文献[17]。
2 混凝土重力坝模态识别的工程经验
表1 是根据相关学者研究成果整理的不同混凝土重力坝模态识别结果的统计。利用最小二乘法对坝高与第一阶自振频率进行线性拟合,得到第一阶自振频率f和坝高h的线性经验关系式为:
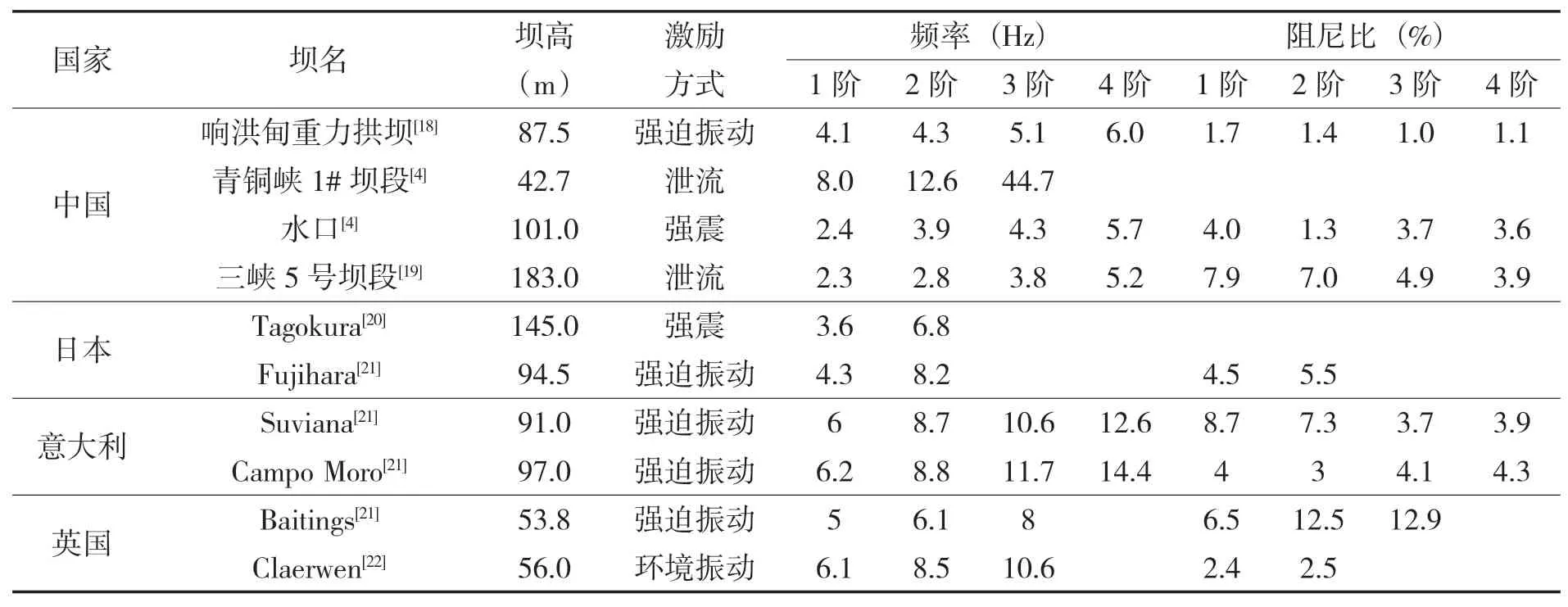
表1 国内外部分重力坝系统识别结果的统计
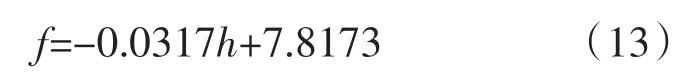
该线性拟合公式的拟合优度R2=0.5548,拟合结果如图1所示。
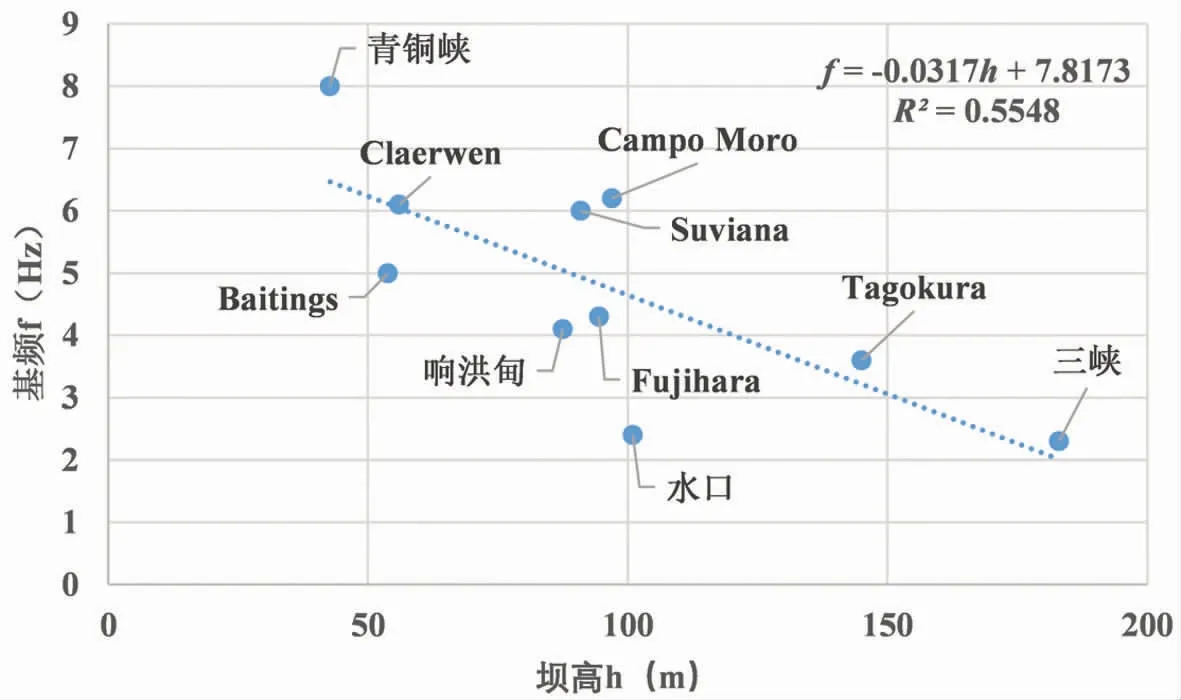
图1 坝高与第一阶频率线性拟合图Fig.1 Linear fitting diagram of dam height and first-order frequency
3 水口重力坝及其振动观测系统
福建省水口水电站位于福建省闽江干流中游,是华东地区最大的水电站,于1993年建成,是以发电为主兼有航运、过木等综合利用的大型水利工程。混凝土重力坝全长870.0m,高101.0m,正常蓄水位为65.0m,设计水位为65.0m,校核洪水位为67.7m,电站装机容量为1400MW。该工程临近台湾海峡强震带,大坝上共布置了7个强震仪进行监测,自由场设在右坝肩基岩上,如图2(a)所示。本文选用19#坝段上的四个强震仪SE1-SE4的观测数据进行分析研究。这些强震仪共有9个观测通道,布置情况如图2(b)所示。
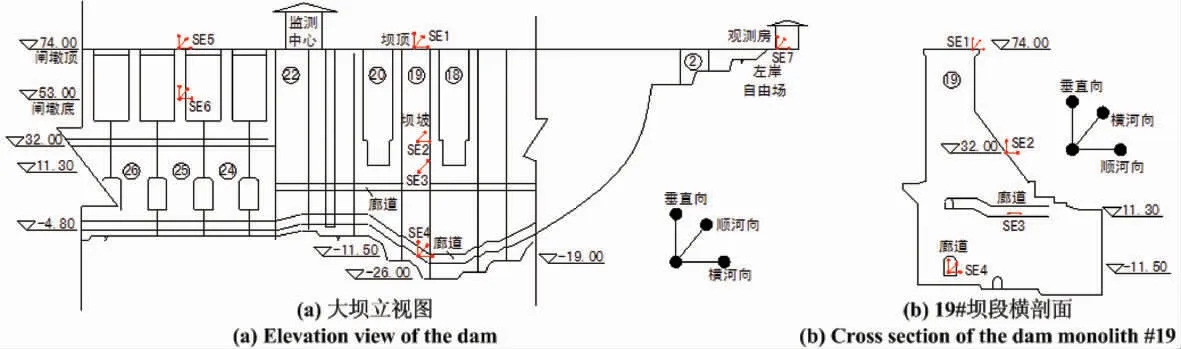
图2 水口重力坝强震仪布置图Fig.2 Layout of strong motion instrument for Shuikou gravity dam
自2003年大坝强震观测系统的改进以来,水口库区地震监测台网共记录到2级以上(含2级)地震50次,3级以上(含3级)地震23次,其中,最大的是2008年3月6日的古田地震,其震级为4.8级。本文选取表2所示的三次具有代表性的地震记录进行分析。图3是三次地震中SE1顺河向观测通道的记录。大坝强震观测系统还定时采集结构的环境激励振动。本文选择四次环境振动监测数据进行分析。图4是SE1强震仪的水平顺河向的环境振动监测数据。地震记录和环境激励振动监测的采样频率为100Hz,记录时长为140s至160s。
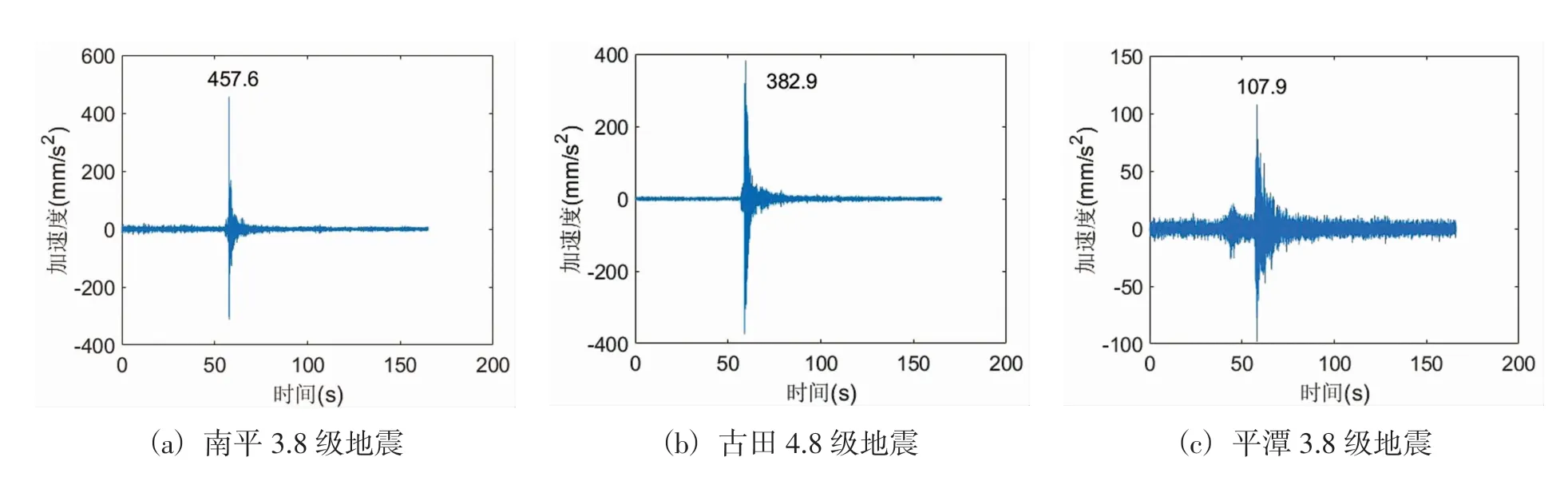
图3 三次地震的SE1强震仪水平顺河向强震记录图Fig.3 Strong earthquake record of SE1 strong motion instrument with three earthquakes along the river
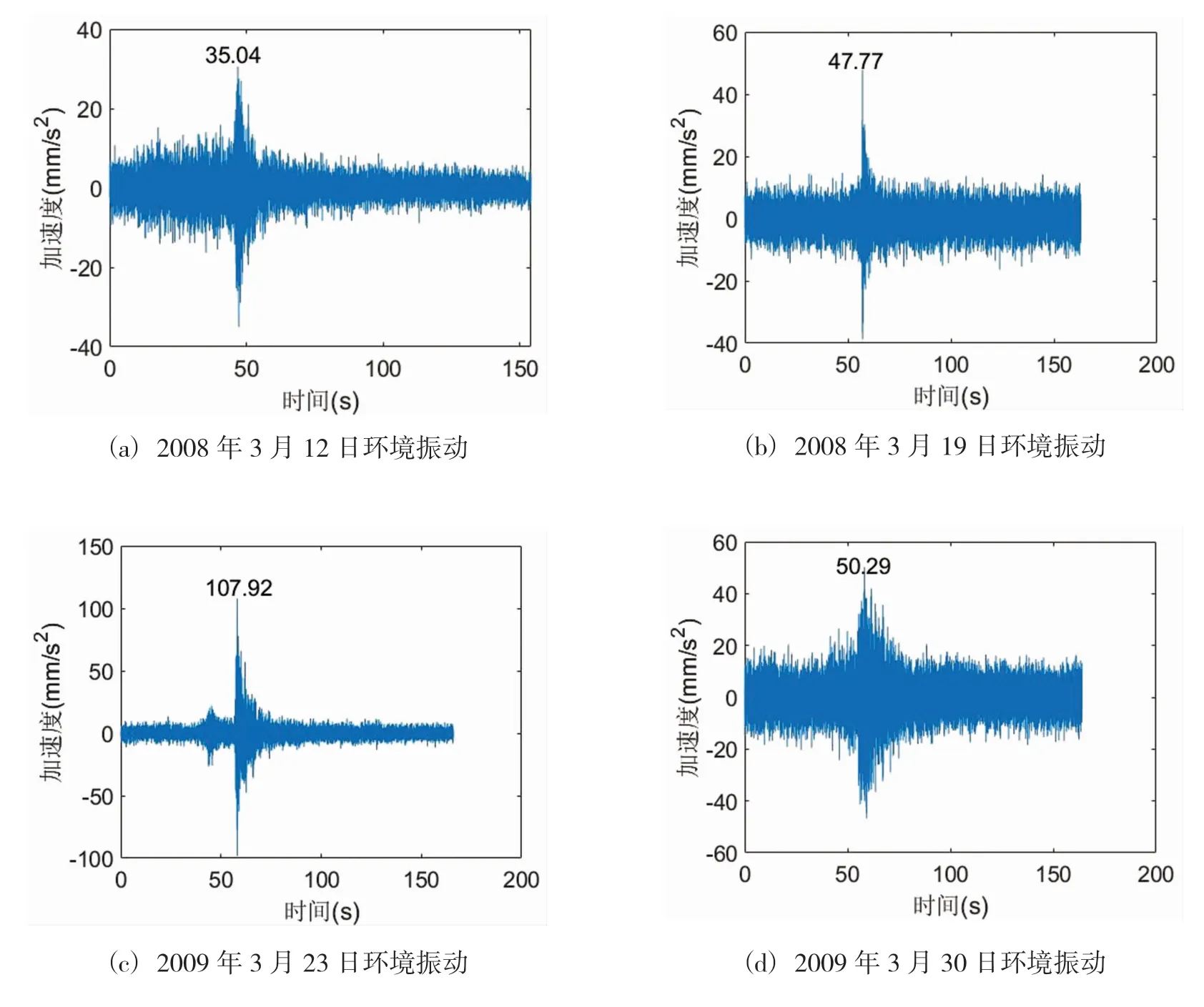
图4 四次环境振动的SE1强震仪水平顺河向振动记录图Fig.4 Vibration record of SE1 strong motion instrument with four environmental vibrations along the river

表2 三次典型地震记录
4 水口重力坝模态识别结果分析
4.1 频率和阻尼识别结果分析
当采用IO类方法进行模态识别时,将大坝左岸自由场的SE7强震仪的顺河、垂直、横河三个通道的观测数据作为模型输入,19#坝段上的SE1-SE4四个强震仪9个通道的观测数据作为模型输出。图5是基于水口水电站三次地震记录计算的频响函数图。频响函数计算时以SE7顺河向为输入。表3是基于前文所介绍的三次大地震,利用ERA-IO、ARX、SSI-IO三种不同的IO方法识别出来的自振频率和阻尼比。
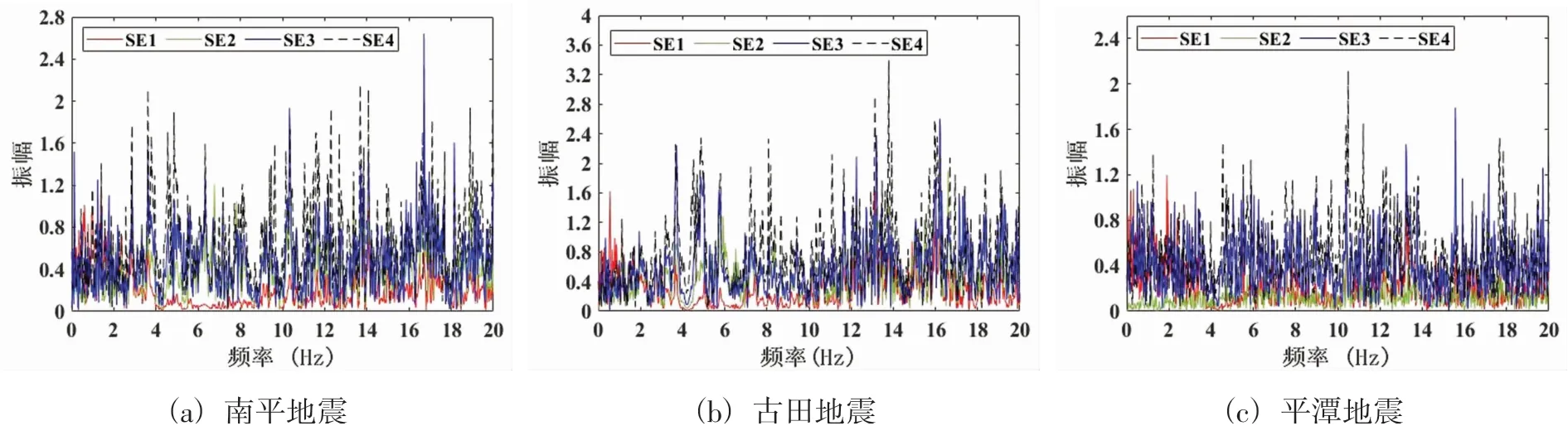
图5 三次地震频响函数图Fig.5 Frequency response function of three earthquakes
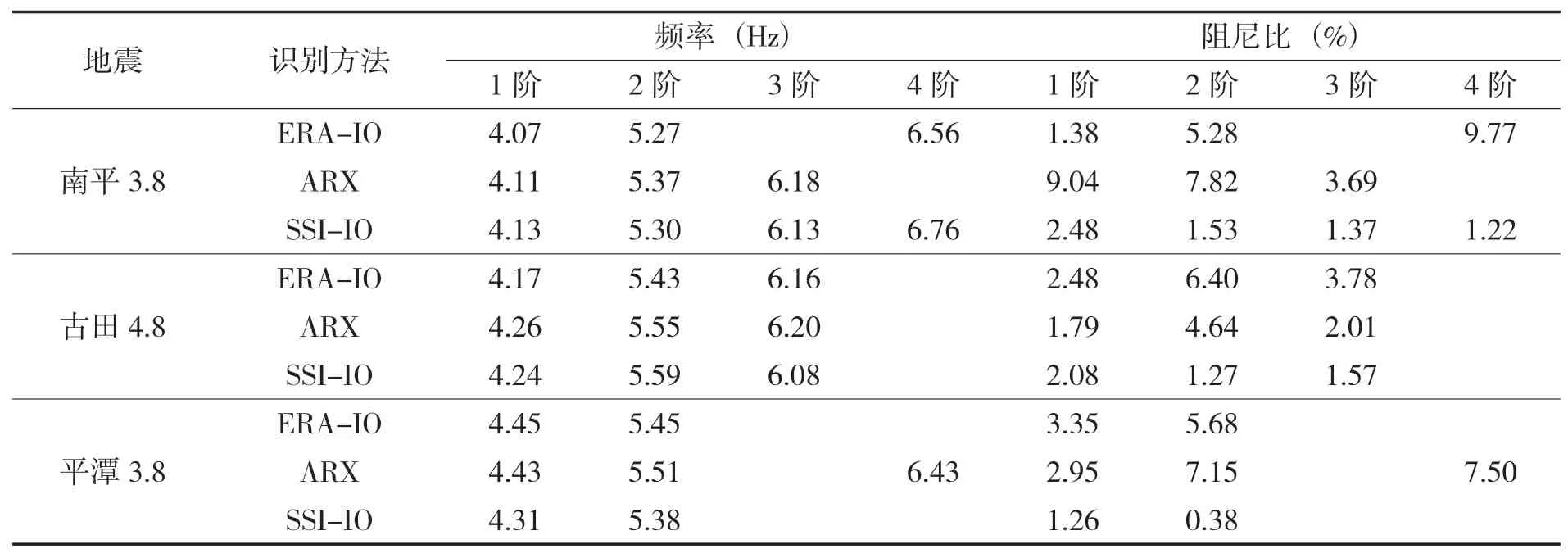
表3 利用IO法对三次地震观测数据识别频率和阻尼的识别结果
(1)大坝基频范围为4.07~4.45Hz,利用前文拟合的经验公式(13)得到的水口重力坝的基频估值为4.62Hz,说明本工程重力基频的识别结果符合一般工程经验。
(2)利用不同识别方法得到的各阶频率大体相同,但有一定的差值。以南平地震为例,第一阶频率最大绝对值差值为0.06Hz,第二阶为0.10Hz,第三阶、第四阶均有一种方法无法识别出对应频率。这是因为相较于低阶模态,高阶模态在地震中的激励响应要小很多,模态识别的结果不如低阶。阻尼比的识别结果并不理想,以古田地震为例,第一阶阻尼比最大绝对值差值为0.69%,第二阶为5.13%,第三阶为2.21%。阻尼比差值与模态阶数之间并没有显著规律,需进一步研究阻尼比的识别问题。
(3)利用同一方法对不同地震激励的识别结果不同。以SSI-IO的识别结果为例,南平地震识别出了前四阶频率,古田地震仅识别至第三阶频率,平潭地震仅识别出前两阶频率。因为三次地震中南平地震的各通道加速度最大,激励输入能量最大,对于高阶模态的激励效果最好,可以识别出更多阶模态。对比前两阶频率的识别结果,南平地震识别频率分别为4.13Hz和5.30Hz,为三次地震最低;古田地震和平潭地震识别频率各有高低。因为相较于后两个库水位相近的地震,南平地震发生时库水位最高,导致其识别的各阶频率较低。
采用OO类方法进行模态识别时,将19#坝段上的SE1-SE4四个强震仪9个通道的观测数据作为模型输出。图6是两个利用ERA-OO进行模态识别的稳态图。表4是基于四次典型环境振动激励监测数据,分别采用ERA-OO、FDD、SSI-OO三种不同的OO类方法识别出的结构自振频率和阻尼比。由表4可知:
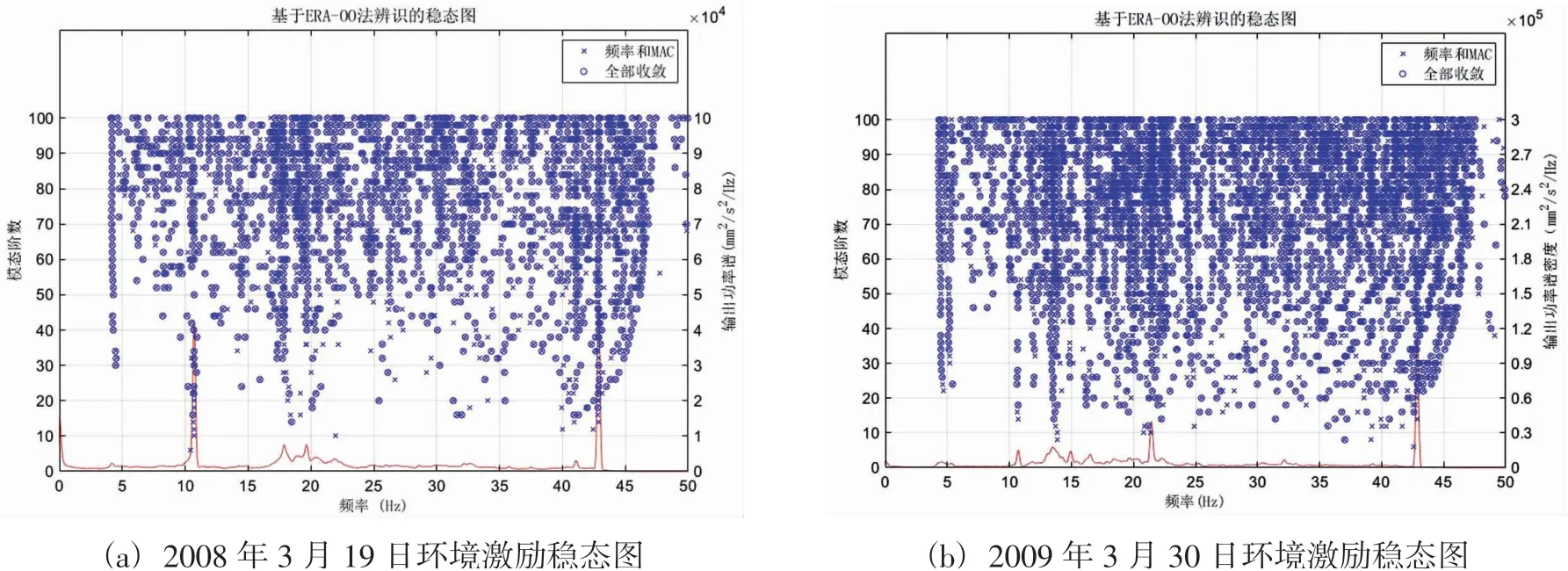
图6 不同环境激励采用ERA-OO方法识别的稳态图Fig.6 Steady state diagram identified by ERA-OO method under different ambient excitation
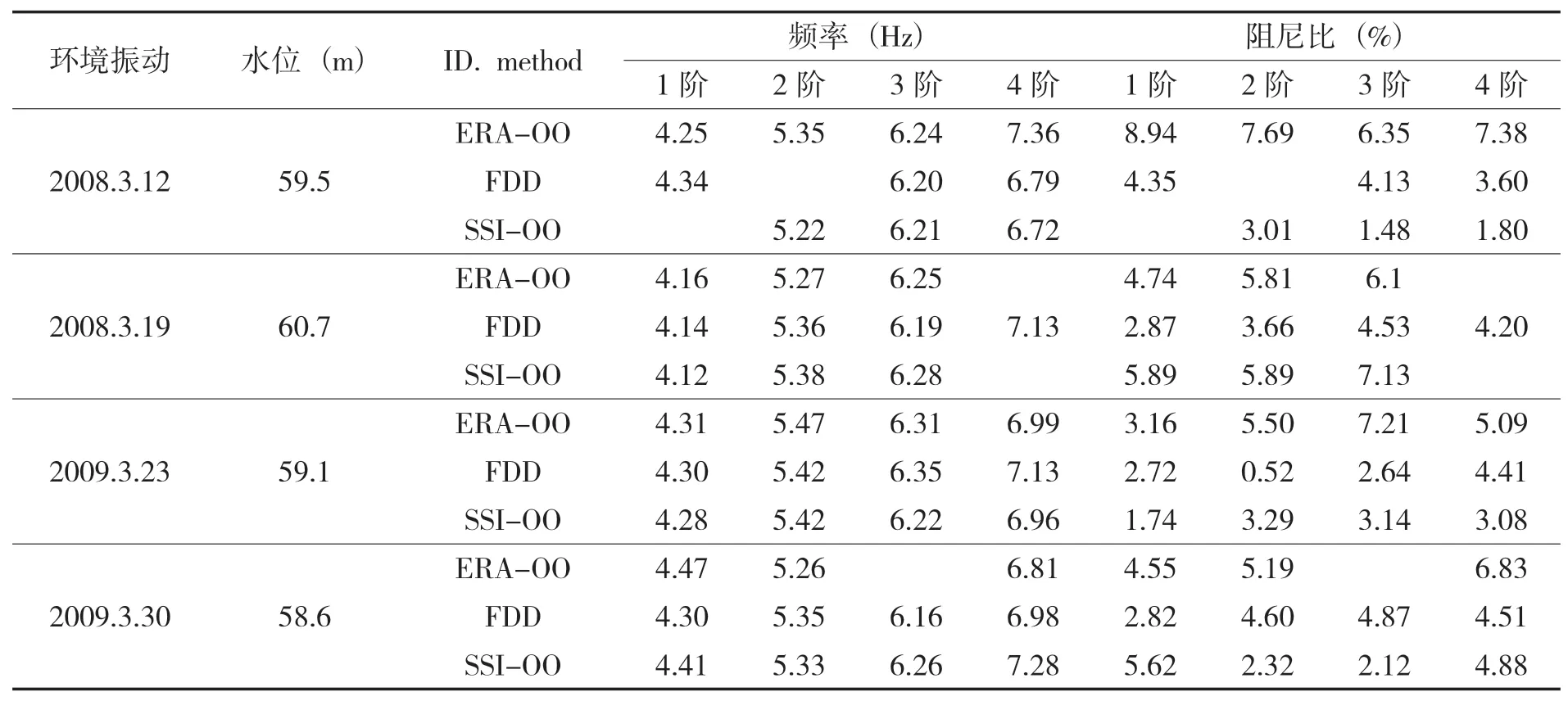
表4 利用OO法对四次环境振动观测数据识别频率和阻尼的识别结果
(1)大坝基频范围在4.12~4.47Hz之间,与前文基于地震激励的识别结果类似,基本符合经验的范围。
(2)以2009年3月23日环境振动为例,第一阶频率最大绝对值差值为0.03Hz,第二阶为0.05Hz, 第三阶为0.13Hz, 第四阶为0.17Hz。随着阶数提升,不同方法的识别频率差值逐渐变大,这也同样验证了前文高阶模态识别难度高的结论。阻尼比识别结果仍旧不理想,不同方法识别的阻尼比差值均远大于频率。将表4利用OO法的识别结果与表3利用IO法的识别结果整体进行对比,OO法的识别结果更加完整,但是其对第四阶频率的识别结果绝对差值较大(0.64Hz)。
(3)选取发生在同一天的平潭地震和2009年3月23日环境振动的SSI识别结果进行对比。如图6所示,两者前两阶的识别结果十分接近,最大频率差值仅为0.04Hz,基于环境激励的低阶识别结果与基于地震识别结果相近。
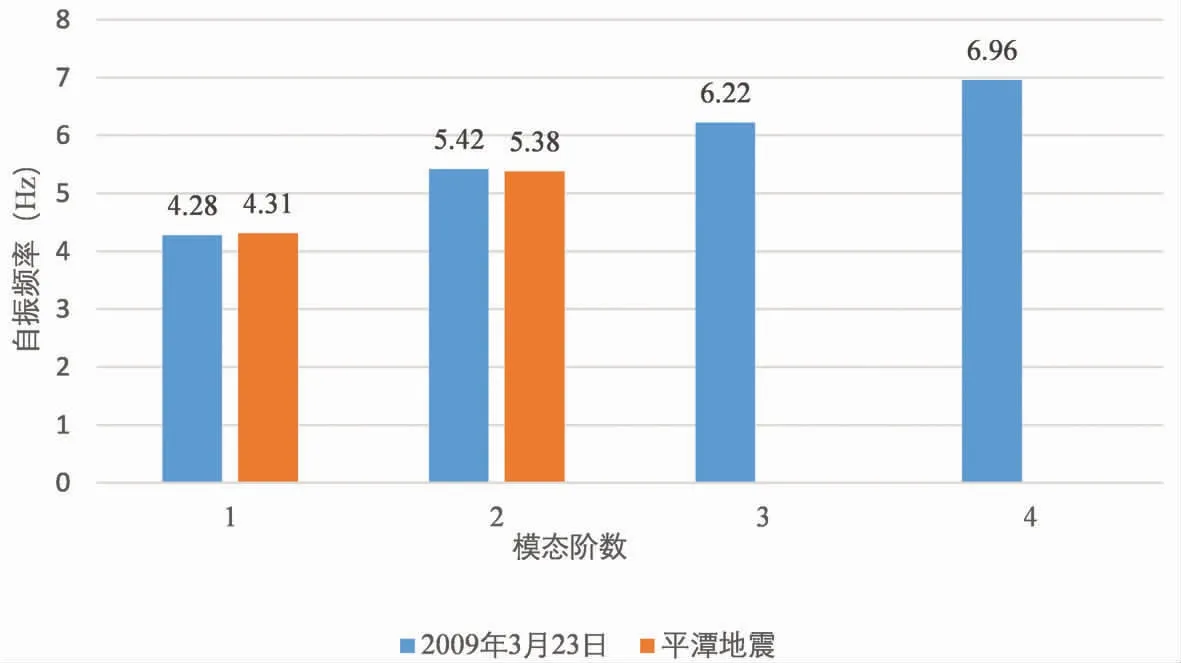
图7 平潭地震和2009年3月23日环境振动SSI识别结果对比图Fig.7 Comparison of SSI-OO identification results of Nanping earthquake and environmental vibration on March 23,2009
总而言之,利用OO法对环境振动进行系统识别虽然可以得到结构弹性状态下的模态参数,且识别结果较为完整,但是由于环境振动相对于地震振幅较小,存在的白噪声影响相对较大,利用不同方法的高阶识别结果差距较大。但是就前两阶的识别结果而言,利用不同方法的环境激励识别结果基本一致。相较于地震激励信号,环境激励信号显然更易获得,可以通过大量的环境振动激励信号识别,得出可靠的结构模态参数,这是利用原型地震激励进行系统识别所不具备的条件。
4.2 振型的识别结果分析
图8 是南平、古田、平谭三次地震利用ARX、ERA-IO和SSI-IO三种方法识别的第一阶振型计算的模态置信因子(MAC)。由图8可以看出,不同方法计算的MAC值在0.65~0.99之间,说明不同方法识别的振型有一定的差异。
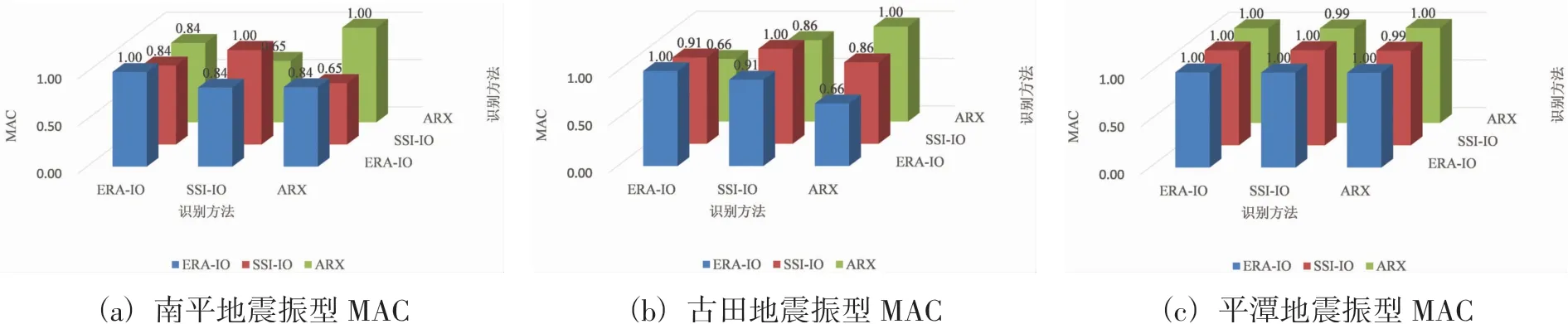
图8 采用不同方法识别的结构第一阶振型的对比Fig.8 Comparison of the first mode shapes of structures identified by different methods
5 结论
本文对不同的地震记录和环境振动记录采用了不同的识别方法,对水口重力坝的模态识别结果进行分析,主要结论如下:
(1)采用环境振动激励和地震激励的模态识别结果有一定差异。虽然环境激励的识别结果有较高的准确度,但是由于环境振动振幅较小,包含频率较少,对于高阶的自振频率激励效果不佳。这给利用环境振动激励进行模态识别得到准确的识别结果带来了一定困难。
(2)即便是相同的激励,采用不同识别方法,模态识别结果都有一定的差异。因此如何根据具体情况选用合适的识别方法是今后研究的重要问题。
(3)文中采用的各识别方法识别的阻尼比存在较大差距,结构阻尼比的识别仍是较大的问题。
