水底管道抛石加固过程的DEM-SPH耦合分析

刘 圆， 张普然， 刘 璐， 季顺迎*

(1.中国船级社海洋工程技术中心,天津 300457; 2.大连理工大学 工业装备结构分析国家重点实验室,大连 116024)

1 引 言

在自然界与人类的生产活动中，颗粒-流体耦合现象广泛存在[1]，如滑坡泥石流[2]、水下抛石及冰水耦合等，在地质灾害演变、化工过程和岩土工程中具有重要的研究意义与价值。离散元方法(DEM)是模拟不同形态颗粒的主要方法，能够清晰地描述颗粒离散介质的动力学行为[3]。同时，求解流体的方法多样，目前应用较多的有有限元方法[4]、无网格粒子法[5]和格子-玻尔兹曼方法[6]等。采用数值模拟开展流固耦合计算是重要的研究手段[7]。

早期离散元法的单元形式主要是二维圆盘与三维圆球[8]，为了更好地描述形态各异的真实颗粒的力学行为，发展了许多非球形的几何形态，如多面体[9]、超二次曲面[10]与扩展多面体等。扩展多面体单元能够较好地模拟海冰和碎石等结构。扩展多面体结合了球体与多面体的几何特征，避免了复杂且不稳定的几何判断，提高了单元接触搜索的效率和稳定性[11]。由于单元表面为曲面，扩展多面体间的接触力计算可采用赫兹接触模型[12]。此外，为分析工程中连续的脆性材料破碎为颗粒材料的过程，发展了基于扩展多面体的粘结与破碎模型[13,14]。基于扩展多面体的离散元方法可与多种计算流体的方法耦合，用于颗粒-流体耦合系统的模拟。

流固耦合中经常存在剧烈冲击，流体发生大变形。SPH方法采用无网格的拉格朗日粒子模拟流体的动力学过程，能够有效避免网格畸变并可自适应地模拟自由表面[15]，SPH方法和DEM方法的基本计算单元均是相似的离散粒子，数据结构和算法逻辑具有较高的相似度，在程序编译与计算方面具有显著优势[16]。

DEM-SPH耦合模型已经成功应用于多个领域，包括海洋工程、生物力学与水利工程等。具体实例包括海浪冲击消波块[17,18]、植物细胞干燥过程[19,20]和毛细血管中血细胞的运动[21]等。DEM-SPH方法的有效性和准确性也在与试验和传统数值结果的比较中得到了充分的验证[22-24]。

水下抛石过程是海洋工程和水利工程中常见的问题，抛石法是工业界保护水底管道的主要方法[25]。本文采用基于扩展多面体的离散元方法模拟碎石块，采用弱可压缩的SPH方法模拟流体，并采用边界排斥力模型计算扩展多面体与SPH粒子间的相互作用，从而建立了碎石块与水相互作用的DEM-SPH耦合方法。为模拟卸料斗中落石与水底管线的碰撞过程，建立了扩展多面体和SPH粒子与锥形结构的接触搜索方法。采用DEM-SPH方法分析了碎石块通过锥形结构入水并与水底管道的作用过程，分析了卸料斗静止与运动时对管线的冲击力和管线周围落石堆积形态的影响。

2 DEM-SPH耦合模型

2.1 扩展多面体单元模型

如图1所示，对球体和任意形状多面体进行闵可夫斯基求和运算，即可构成扩展多面体。其中，多面体称为基本多面体，球体称为扩展球体，球体半径称为扩展半径。扩展多面体将角点和棱边的接触搜索转化为相应的球面和圆柱面搜索，简化了单元间的接触判断过程[26]。

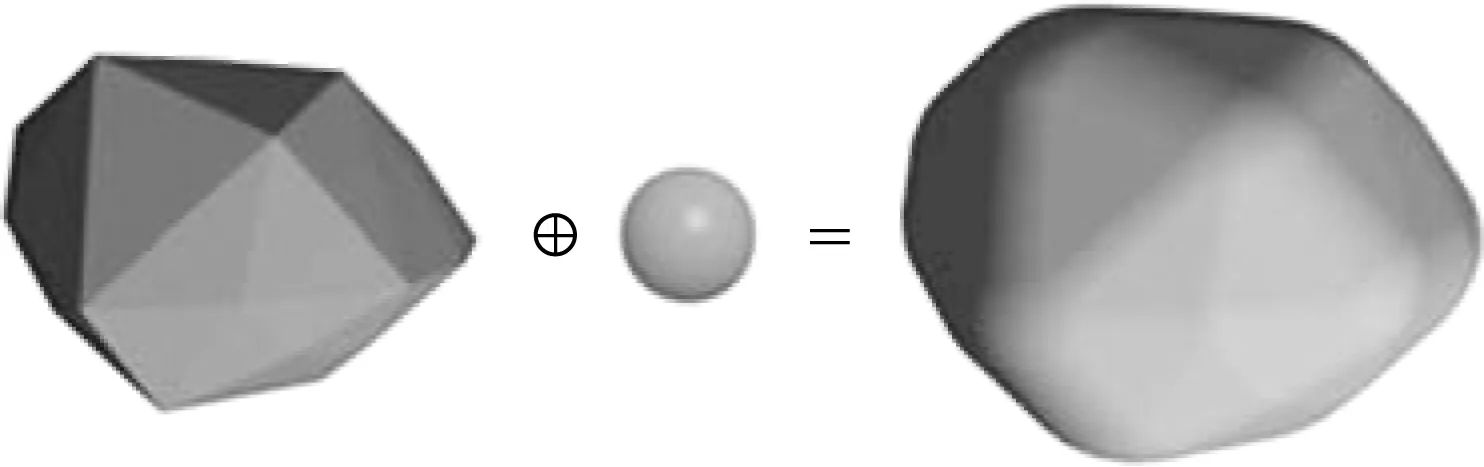
图1 基于Minkowski Sum方法的扩展多面体单元

(1)

式中ri和rj为两个扩展多面体单元的扩展半径。

δi j<0时表示两个扩展多面体发生接触，接触力的计算采用非线性模型，包括法向力和切向力。法向力包含弹性力与粘滞力，可表示为

(2)

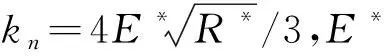
(3，4)

式中ks为单元间切向有效刚度，且ks=rs nkn，而rs n=1/(2+2ν)，ν为泊松比，δs为切向位移，μ为滑动摩擦系数。

2.2 弱可压缩SPH方法

弱可压缩SPH方法在流体动力学的数值模拟中得到广泛应用。流体粒子密度的连续性方程为

(5)

式中ui j为粒子i与j之间的速度差，ui j=ui-uj，W为核函数，本文采用三次样条核函数。每个粒子的压力可通过状态方程计算，即

(6)

(7)

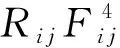
2.3 离散元颗粒与SPH粒子间的排斥力模型

SPH方法中常用的边界粒子法和虚拟粒子法不适用于构造复杂形状的边界[27]。因此，如图2所示，用排斥力方法简化了SPH粒子与扩展多面体之间的相互作用，作用力只与距离d相关。

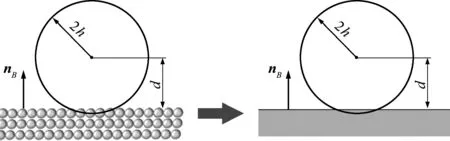
图2 SPH粒子与固体边界之间的排斥力模型

fB=βnBε(z)R(d)

(8)

式中fB为边界排斥力，β为控制系数，nB为壁面边界法向量，ε(z)为与粒子的z方向坐标有关的压力校正项，d为SPH粒子与边界之间的最小距离，R(d)为排斥力函数，可表示为

(9)

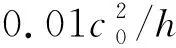
2.4 扩展多面体与锥形结构间的接触判断

本文采用锥形结构来模拟海底管线以及卸料斗，建立了锥形结构与扩展多面体的接触判断方法。由于扩展多面体单元主要由角点、棱边和平面等元素组成，锥形结构外部与扩展多面体单元的接触可分为以下三种类型。(1) 球体与锥形结构接触；(2) 圆柱体与锥形结构接触；(3) 平面与锥形结构接触。锥形结构内部与扩展多面体单元的接触为球体与锥形结构接触。

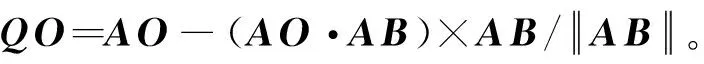
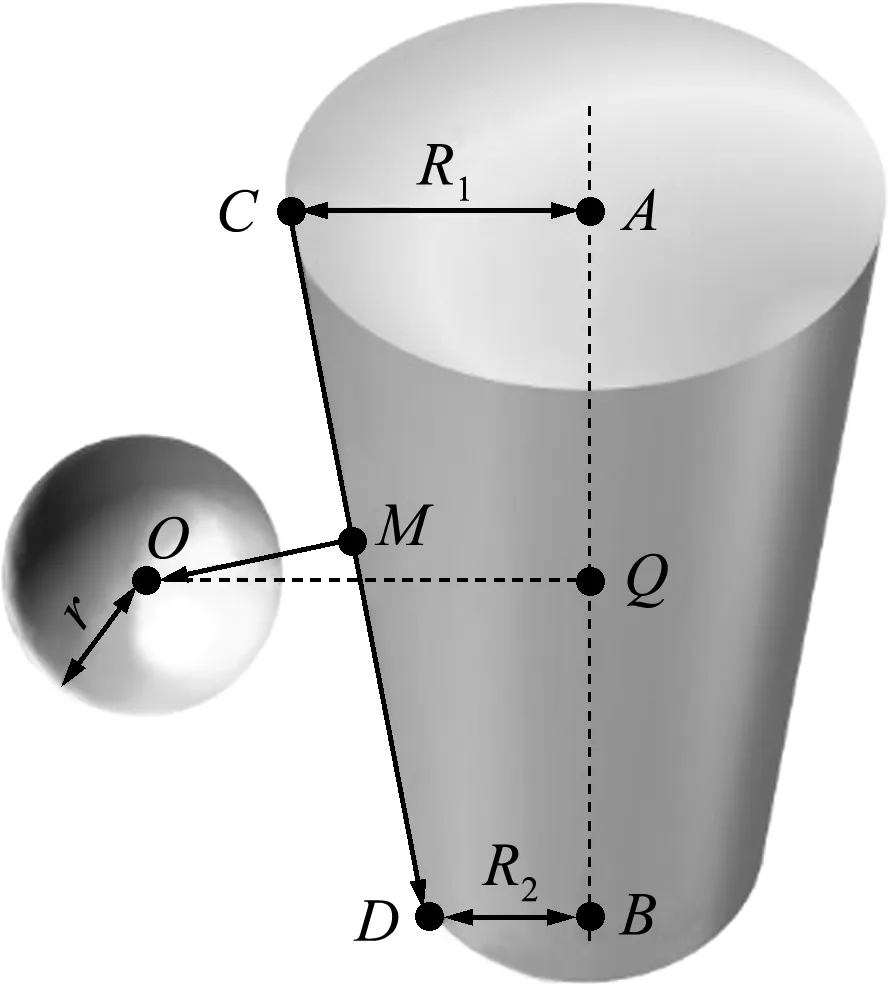
图3 球体与锥形结构间的接触

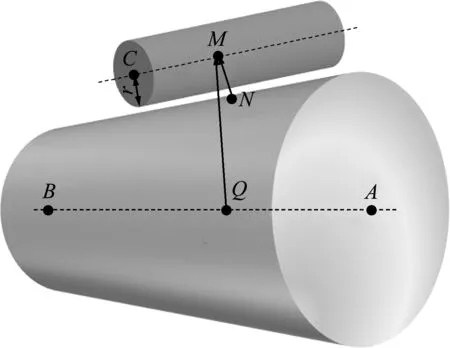
图4 圆柱与锥形结构的接触判断

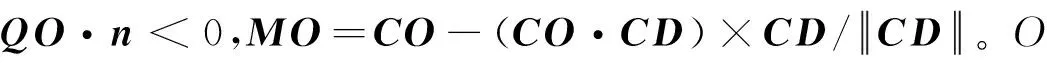
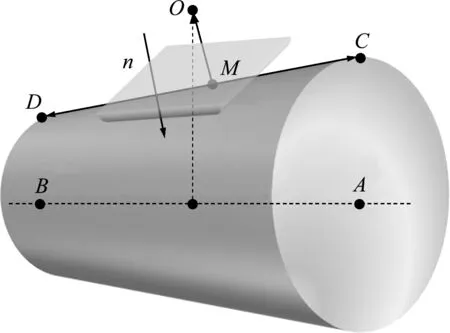
图5 平面与锥形结构的接触判断

3 DEM-SPH耦合方法的验证

3.1 溃坝模拟

三维溃坝流的计算模型如图6所示，水坝的z方向长度H=0.6 m，x方向长度L=2H，y方向长度W=3H。长方体容器的z方向长度D=3H，x方向长度d=5.366H，y方向长度与溃坝相同。SPH粒子光滑长度为0.015 m，粒子总数为25600。

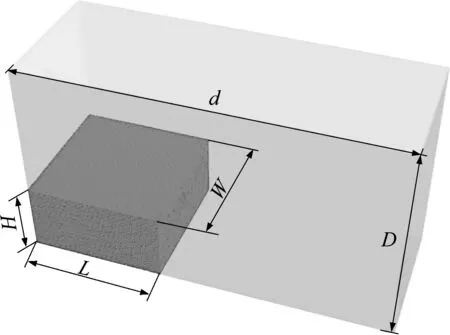
图6 溃坝计算模型

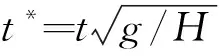
图7 溃坝过程的SPH模拟

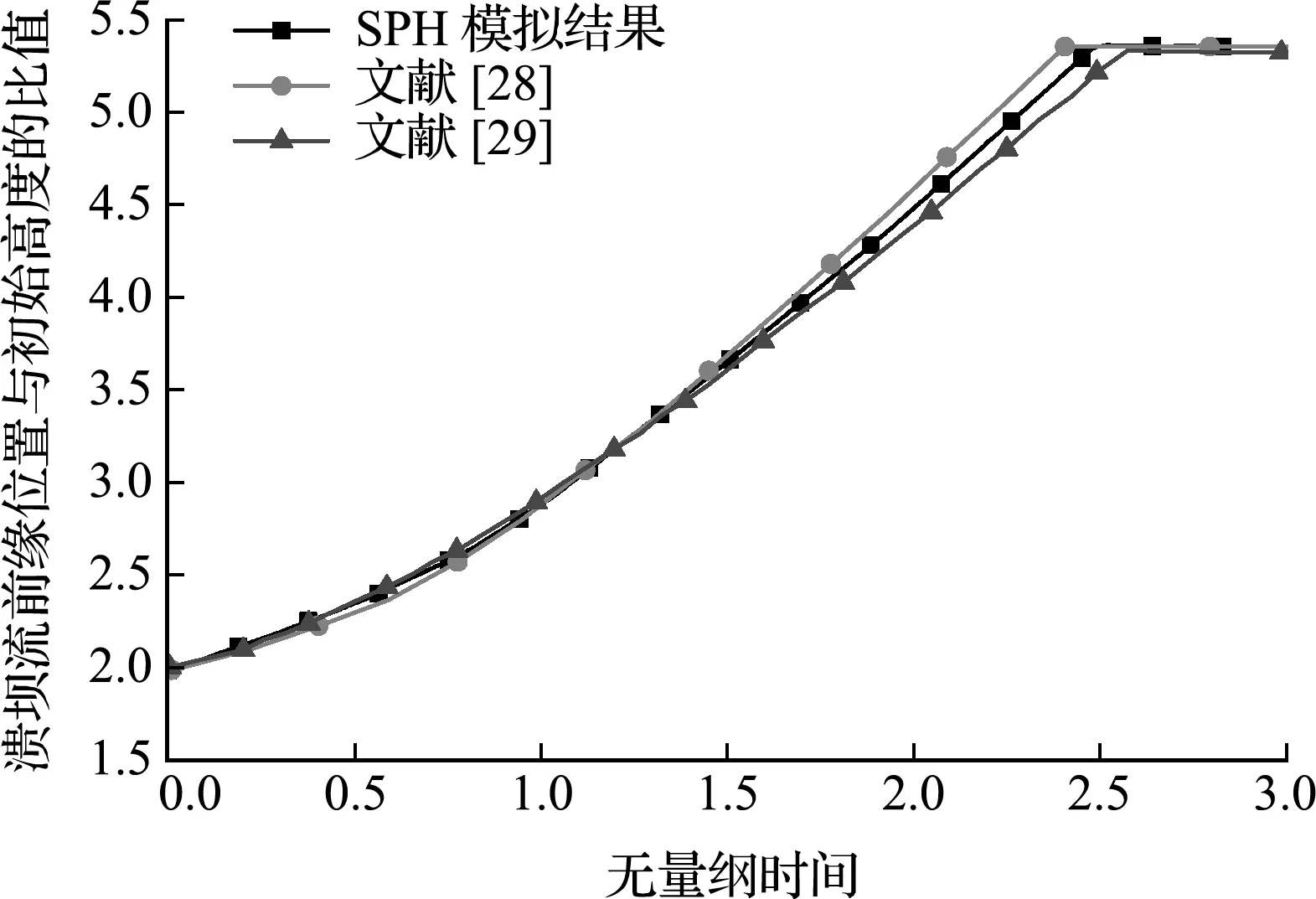
图8 溃坝流前缘位置随时间的变化

3.2 楔形块入水模拟

楔形块入水是结构物入水问题的经典算例，已有大量的工作对其开展了研究，包括理论、试验与数值模拟，因此通过该算例验证DEM-SPH耦合方法的合理性。参考Lewis等[30]的试验，模型尺寸如图9所示，楔形块的质量为23.4 kg，平均密度为336.89 kg/m3。边界长度为2.0 m，宽度比楔形块宽度稍大一些，为0.76 m。水深0.59 m，楔形块最底部位置距水面高度为0.5 m。

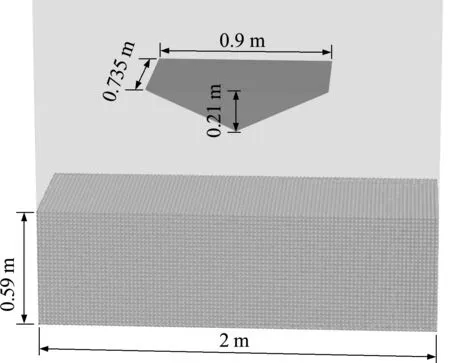
图9 楔形块入水模型

研究不同SPH粒子光滑长度下楔形块加速度随时间的变化，并与试验结果进行了对比，如图10所示。由于试验中存在空气阻力与试验装置的摩擦，楔形块未入水之前的加速度略小于重力加速度。当光滑长度取0.01 m或0.02 m时，模拟结果与试验结果较为接近，验证了DEM-SPH耦合方法的合理性。当光滑长度扩大到0.05 m时，加速度峰值相较于试验结果有明显下降。实际上，DEM单元与SPH粒子的粒径比越大，模拟结果越接近实际情况，但是SPH粒子过多时计算效率会显著下降，因此DEM单元与SPH粒子的粒径比一般保持在8～15之间。

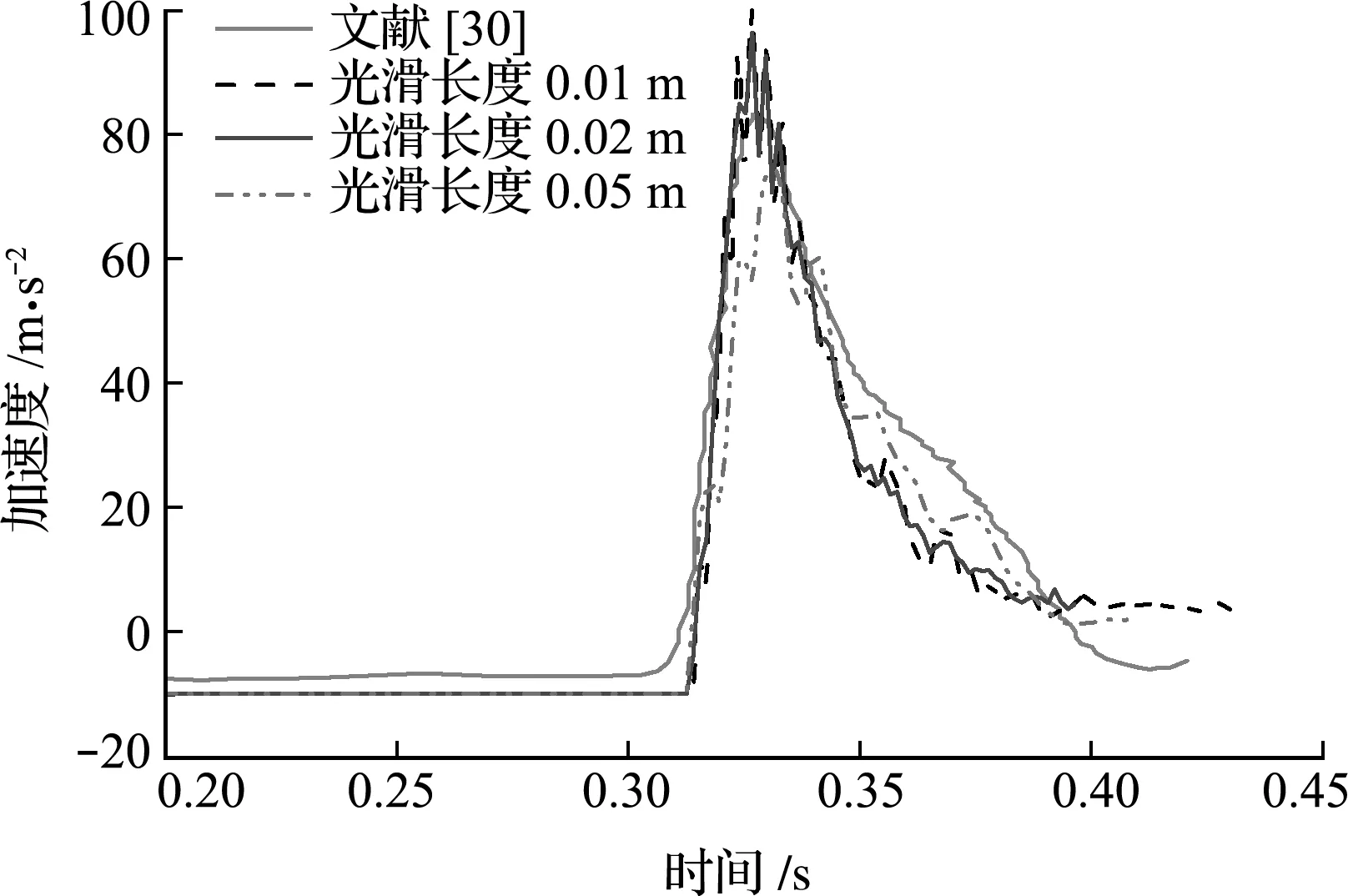
图10 不同光滑长度下的加速度

4 水底管道抛石加固的流固耦合模拟

铺设在海床上的海底管道或电缆通常需碎石掩埋，以增强管道的稳定性并保护管道，使其免受侵蚀与冲击。该过程通常是通过船舶上的落石装置将碎石倾倒在管道上[31]，如图11所示。管道周围落石的数量与堆积形态对于评估落石是否对管道提供了足够的约束具有重要意义。采用本文提出的DEM-SPH耦合方法模拟落石过程，并研究卸料斗静止与运动时落石的堆积形态。

图11 水底管线落石过程

4.1 模型建立与参数设置

采用Voronoi法(VTA)生成随机形态的扩展多面体用于模拟落石入水过程。根据3.2节的结论，流固耦合模拟过程中DEM单元与SPH粒子的粒径比一般保持在8～15之间。综合考虑实际的结构参数与计算效率，确定模拟过程中SPH粒子的光滑长度为0.05 m，DEM单元的粒径约为 0.4 m～0.6 m。

如图12所示，卸料斗由自上而下的三段锥形结构组成。最下面的落石管深入水面下方，顶部管道用于容纳落石在卸料斗中的堆积。水底管道的直径为0.8 m，其轴线方向为y方向。卸料斗和水底管道都是刚性结构。所有石块最初都放置在卸料斗的顶部管道中，初始状态有竖直向下的初速度，并在重力作用下从管道中掉落。

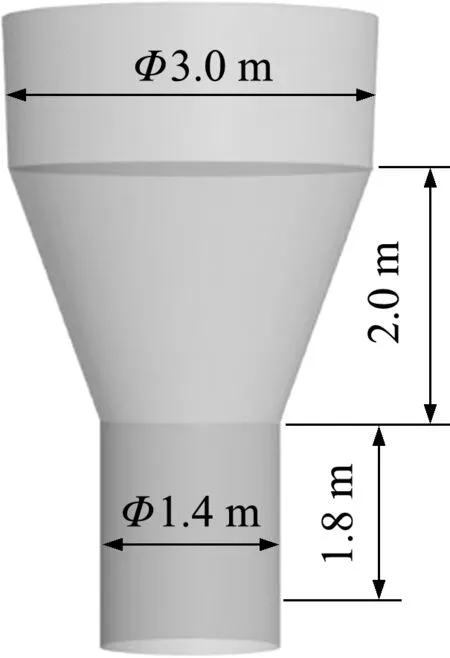
图12 卸料斗

表1 落石模拟中的主要参数

4.2 卸料斗固定的模拟结果与分析

卸料斗的三根锥形结构不发生移动，底部水域边界为4 m×4 m，水深为3 m。该模拟用于验证DEM单元以及SPH粒子与锥形结构间的接触模型。图13显示了落石的模拟过程。其中，石块下落初速度为1 m/s，与卸料斗内部发生接触并落入水中，然后与水底管道发生碰撞，最终落石完全覆盖水底管道。随着水中石块数量的增多，卸料斗底部产生堵塞现象，石块在卸料斗中产生了堆积现象。

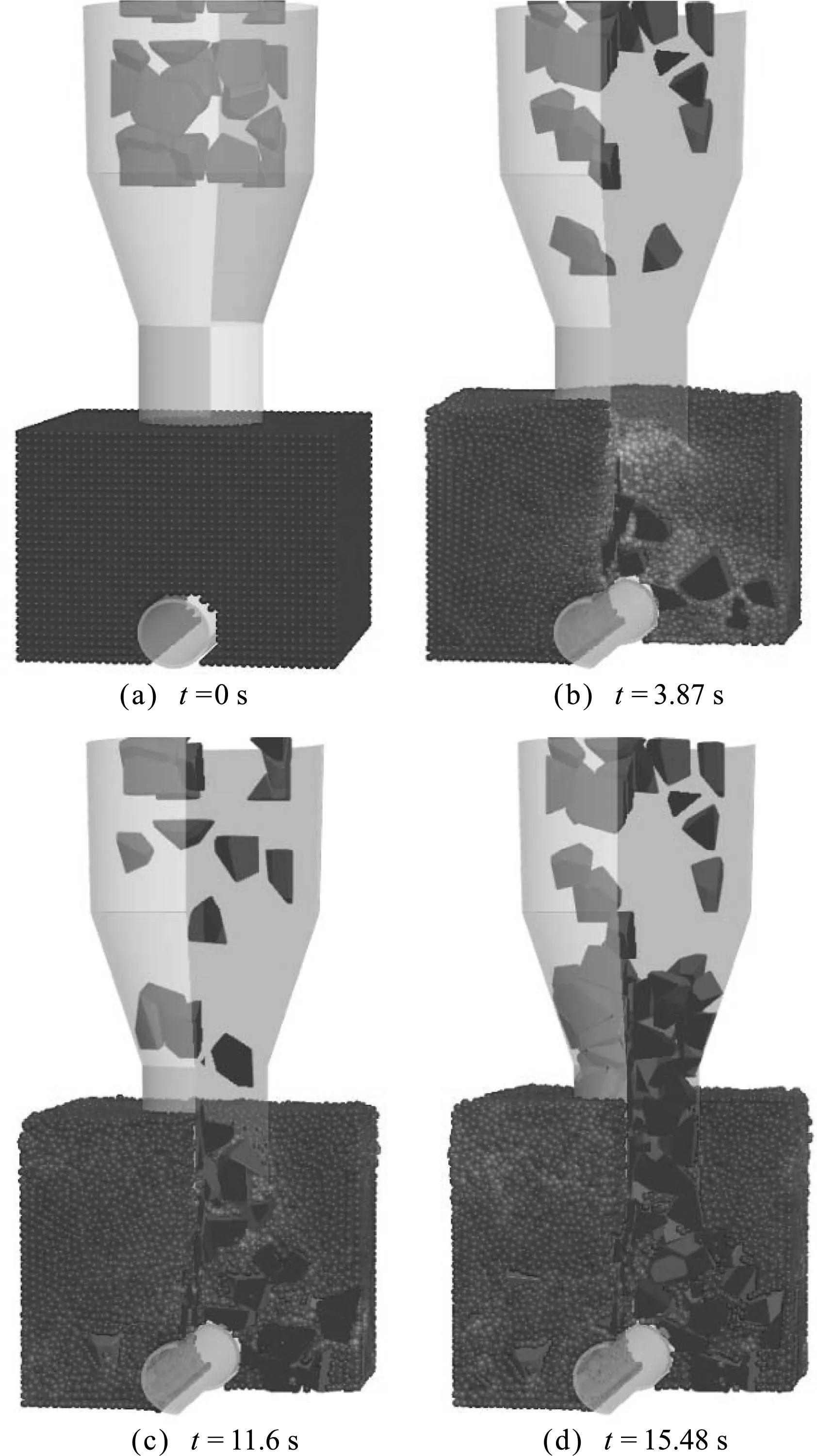
图13 管线落石的流固耦合模拟过程

图14显示了水底管道受到的冲击力，包括落石和水对管道的冲击力。开始一段时间管道只受到水的冲击力，1.2 s开始有落石与管道发生接触，由于边界较为狭小，在t=13 s之后，落石在卸料斗中堆积，无法入水，水底管道附近的落石没有继续增多，因此落石对管的冲击力并未随时间一直增长，反而在堆积稳定后出现下降趋势。开始0～2 s内水对管道的冲击力有一个较大的波动，稳定后水对管道的力在25 kN左右。整个过程中，落石对管道的力基本处于10 kN～30 kN。

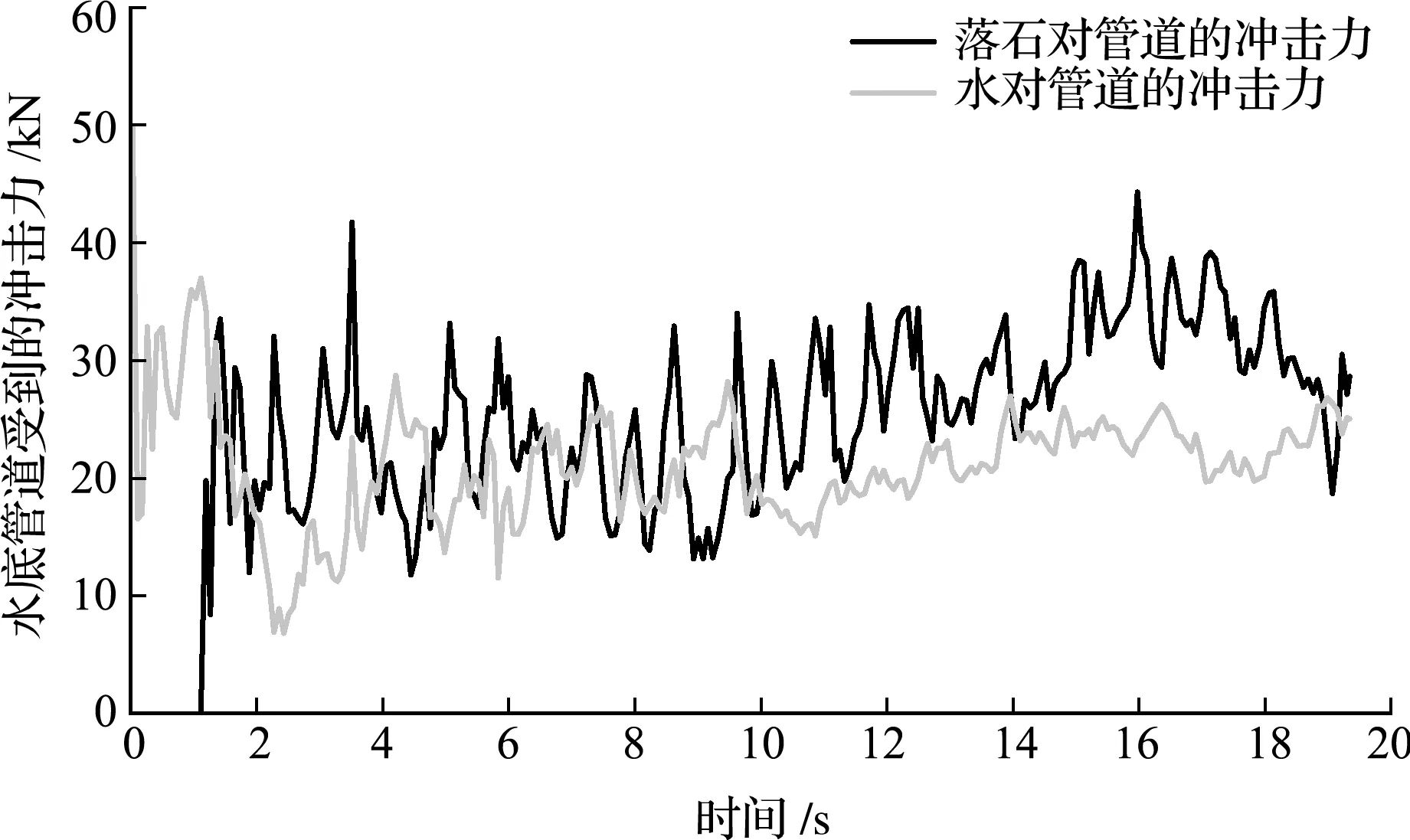
图14 水底管道受到的冲击力

4.3 卸料斗移动的模拟结果与分析

通过4.2节卸料斗固定的模拟，成功验证了石块以及水与卸料斗间的接触模型。而在实际情况中，抛石船会沿着水底管线不断移动，卸料斗也随船一起移动。结合实际情况与计算效率，确定水域大小等参数，模拟了卸料斗边移动边抛石的过程。

卸料斗沿着管道轴线方向移动。底部水域边界尺寸为4 m×10 m，水深为3.0 m。在模拟过程中，落石下落初速度与卸料斗移动速度是两个重要参数，影响落石最终的堆积形态。如图15所示，当卸料斗移动速度较小而落石初速度较大时，很容易出现落石堵塞卸料斗的情况。因此，选取合适的落石初速度与卸料斗移动速度，是成功模拟水下抛石过程的关键。

图15 落石堵塞卸料斗

图16显示了卸料斗速度为0.5 m/s，落石初速度为1 m/s时的抛石过程。卸料斗开始停止，2.36 s后向y轴正方向做匀速直线运动。石块通过卸料斗落入水中，然后撞击水底管道。水底管道上的作用力如图17所示。随着时间的增长，水对管道的作用力趋于稳定，而落石对管道的作用力总体呈不断上升趋势，这表明石块倾倒过程中未出现堵塞的情况。

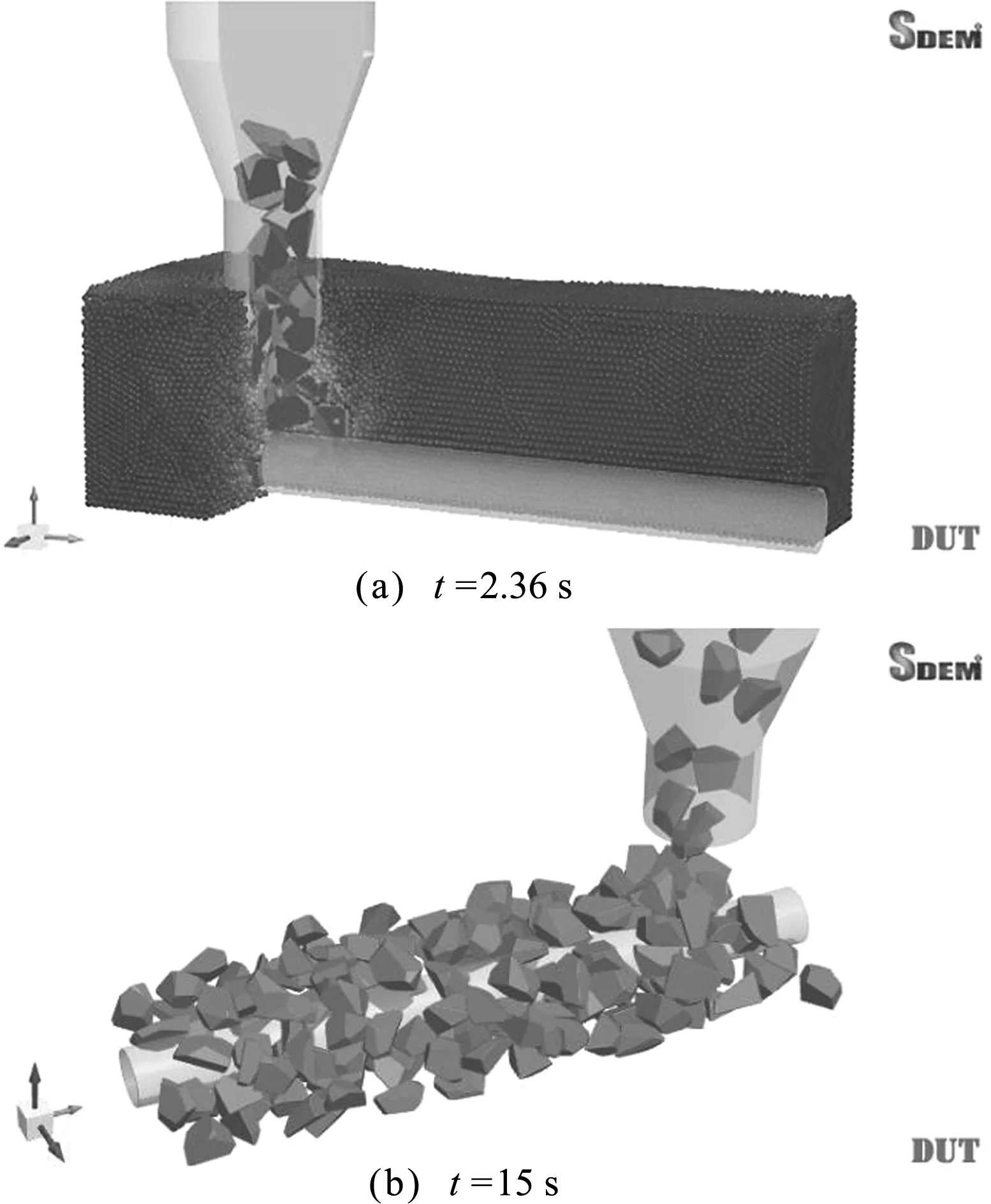
图16 卸料斗移速0.5 m/s时的模拟结果

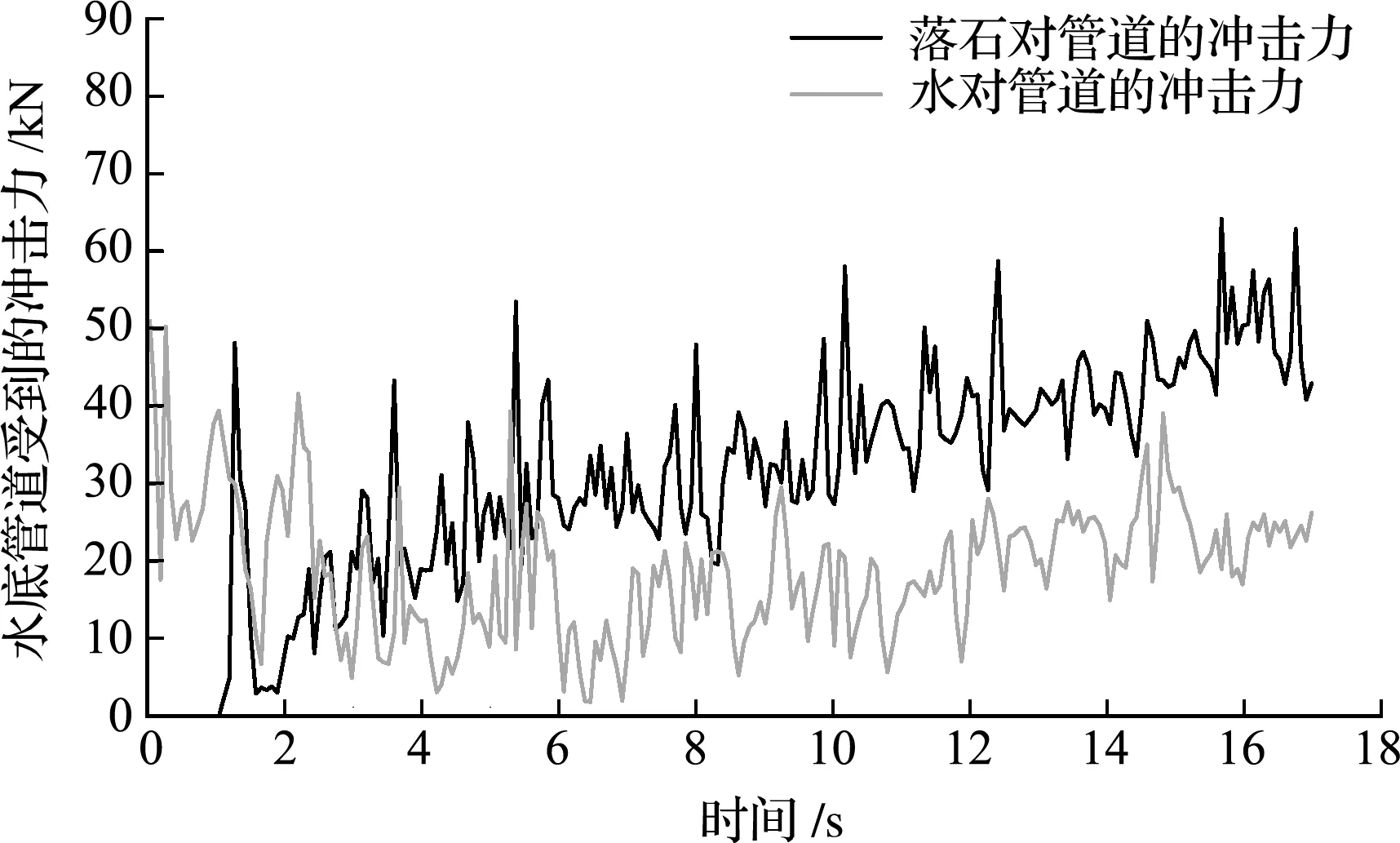
图17 卸料斗移速0.5 m/s时管道受力

如图16(b)所示，抛石结束后水底管道并未完全受落石覆盖，这种情况下落石无法充分保护管道，是工程中必须要避免的现象。保持卸料斗移动速度不变，增大落石初速度，观察抛石结束后落石的分布情况。

图18展示了落石下落初速度为2 m/s和 3 m/s 时的模拟结果。可以看出，在卸料斗移速为0.5 m/s的条件下，落石初速度大于2 m/s时，落石可以完全覆盖管道，15 s后卸料斗到达边界位置，不再移动，此时落石已经开始在卸料斗中堆积，落石对水底管道的冲击力不再增大，与4.2节的情况相同。

图18 改变下落初速度后的模拟结果

当落石初速度取3 m/s和2 m/s时，抛石结束后管道所受冲击力比较接近。这表明在落石已经能够覆盖管道时，随着落石初速度增大，冲击力增大的幅度在减小。由于受抛石模型中边界约束以及卸料斗底部到水底管道的距离限制，覆盖管道的落石数量存在上限。而抛石结束后，管道所受冲击力主要是稳定后覆盖管道落石的重力，因此可以预测，对于本文给出的抛石模型，落石初速度大于 3 m/s 后，落石在管道附近的分布形态以及管道所受冲击力的变化会越来越小。

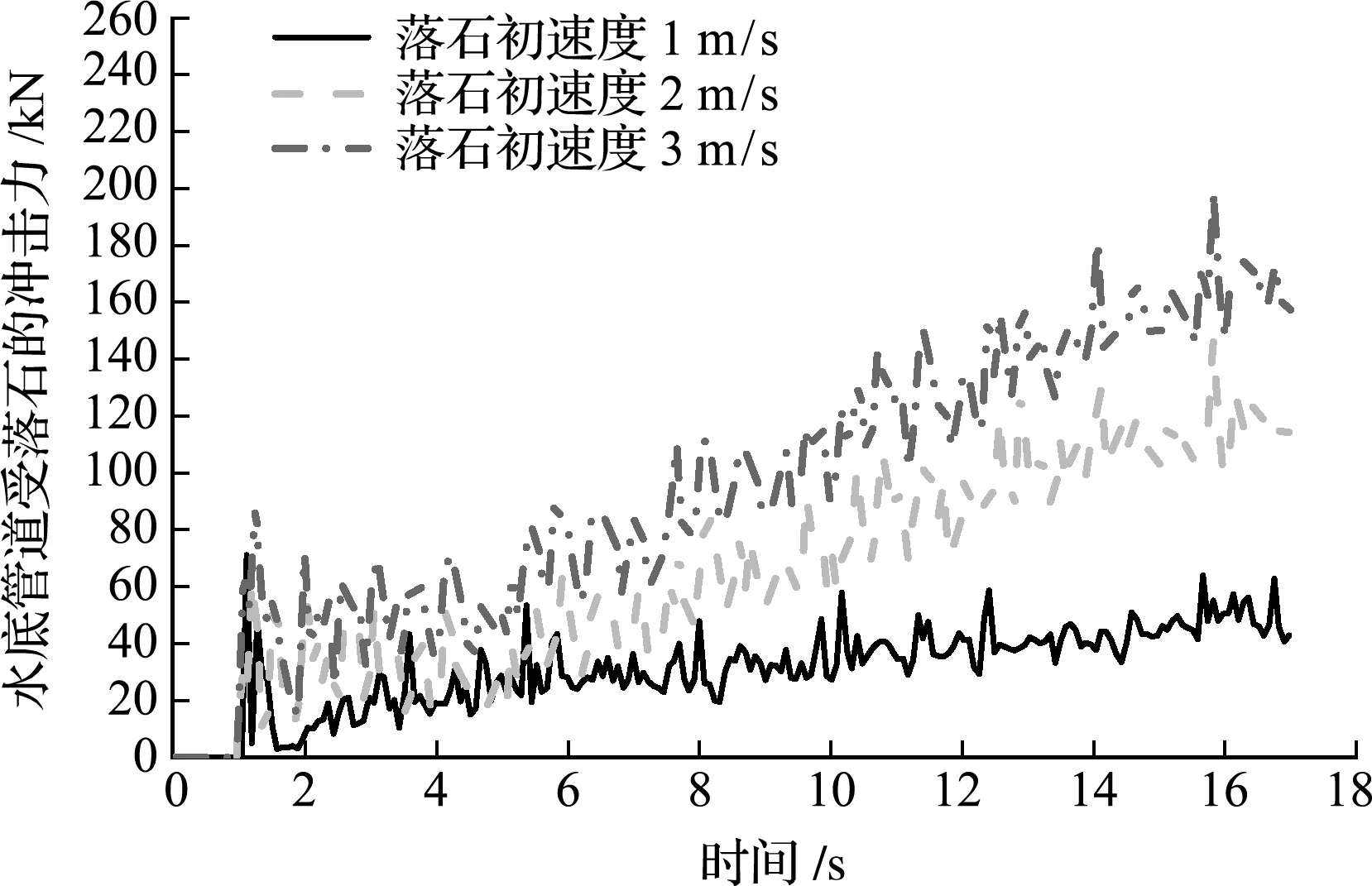
图19 落石初速度不同时落石对管道的冲击力

接下来讨论卸料斗移动速度对模拟过程的影响。落石下落初速度固定为3 m/s，图20展示了卸料斗移动速度为1 m/s和1.5 m/s时的模拟结果。相较于图18(b)，图20中覆盖管道的落石减少很多，图20(b)所示的结果已经属于抛石失败的范畴。

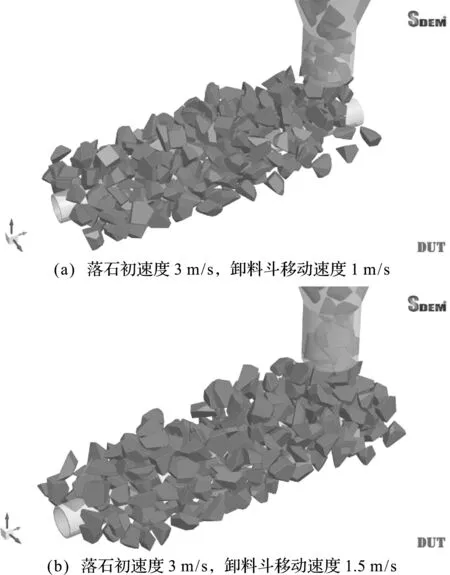
图20 卸料斗移动速度不同时的模拟结果

由于落石初速度相同，单位时间内下落的落石数量相同，因此抛石过程中管道受力随时间的变化曲线基本重合，因此将自变量更改为卸料斗移动的距离。分析了落石对管道冲击力随卸料斗移动距离的变化。如图21所示，卸料斗开始移动时，三个工况下冲击力很接近，抛石过程中，卸料斗移动速度越快，抛石的总量越小，管道受冲击力也越小。其中，卸料斗移速为1 m/s和1.5 m/s时冲击力比较接近，是由于这两种工况下，覆盖在管道上方的落石数量太少，而散落在管道两侧的落石对管道的冲击力基本可以忽略不计。

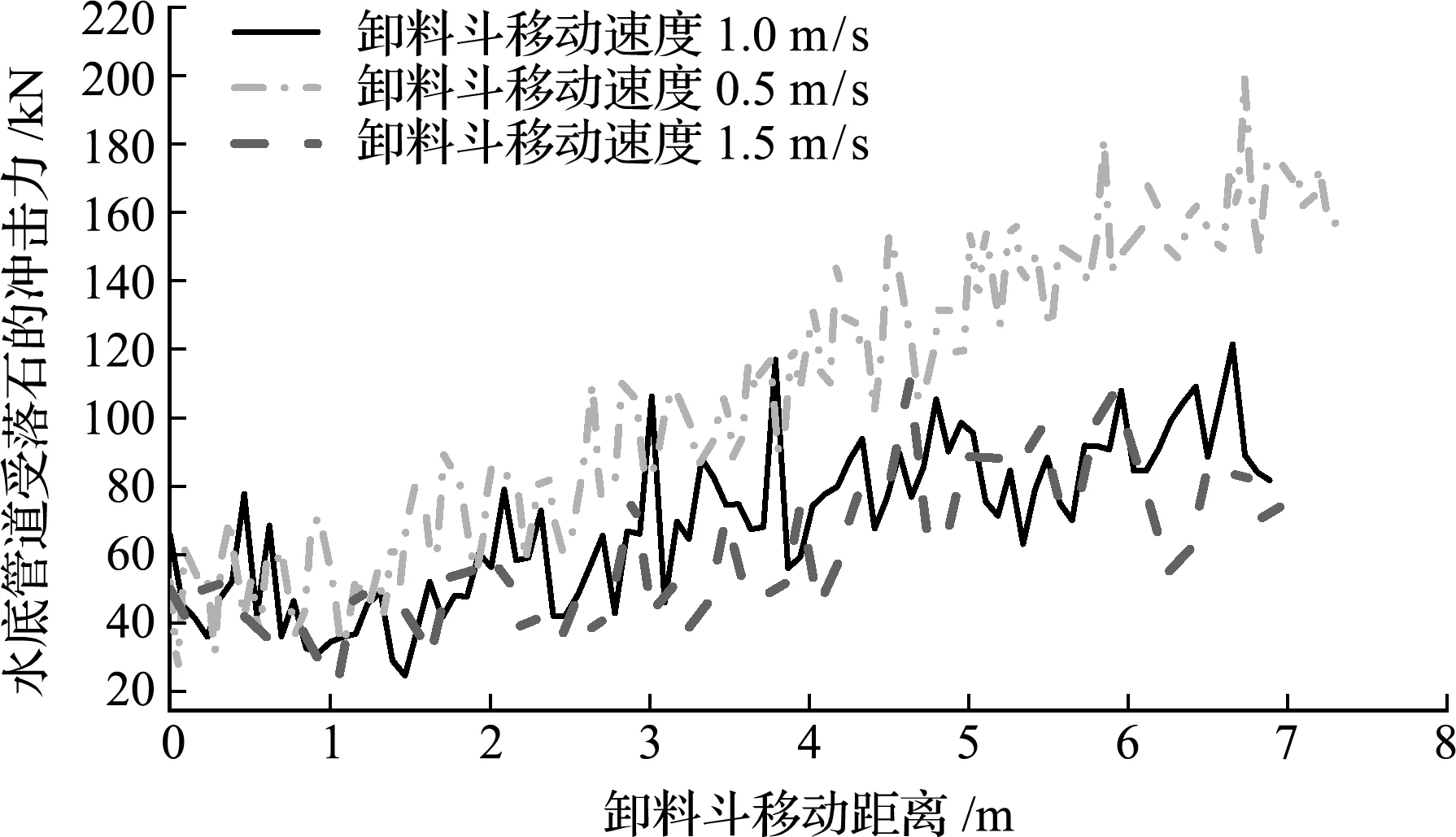
图21 卸料斗移动速度不同时落石对管道的冲击力

对于本文构建的水下抛石模型，通过几组工况的模拟，可以确定当落石初速度取2 m/s～3 m/s，卸料斗移动速度取0.5 m/s～1 m/s时，卸料斗移动抛石结束后落石分布状况较为理想，可以实现管道保护的目标。落石初速度过大会造成堵塞，过小会导致落石无法保护管道，而卸料斗移速对模拟结果的影响与落石初速度相反。在实际的抛石过程中，可以先通过本文提出的卸料斗抛石模型进行多工况的数值模拟，根据结果确定相关参数后再进行作业，可以有效节省人力物力。

5 结 论

本文采用基于闵科夫斯基的扩展多面体单元建立随机形态颗粒的离散元方法，采用弱可压缩格式的SPH方法进行水动力学模拟，并采用排斥力模型计算扩展多面体与SPH粒子之间的相互作用力，从而建立了DEM-SPH耦合模型。通过溃坝及楔形块入水等典型算例验证了本文方法的稳定性和合理性。采用DEM-SPH耦合方法模拟了水底管道落石过程，对水底管道受到的作用力和碎石块堆积形态进行了分析。设定多组工况，探究了落石初速度和抛石船移动速度对抛石结果的影响。计算结果表明，本文建立的DEM-SPH方法可有效模拟落石入水并与水底管道作用的过程，可进一步应用于落石装置设计和水底管道稳定性等工程问题的分析中。