基于自适应融合数据的线路参数辨识
2021-07-01董清,吴敬
董 清,吴 敬
(华北电力大学 电气与电子工程学院,河北 保定 071003)
0 引言
随着电网技术的快速发展和通信技术的信息交换能力的显著提高,电网运行方式变得越来越复杂。电网实际运行过程中调控中心的系统管理处、保护处和自动化处使用的线路参数不同,而准确的线路参数对于潮流计算、状态估计、无功优化和继电保护整定计算应用非常重要[1]。因此,根据实时数据计算获取线路的准确参数有着十分重要的意义。
系统实时运行数据来源主要有基于广域测量系统(WAMS)的终端PMU数据、数据采集与监控系统(SCADA)的终端RTU数据和故障录波数据等[2]。基于离散傅里叶算法的 PMU装置可以实现系统各节点工频电压幅值、相角的测量[3]。文献[4-6]基于 PMU 实测数据辨识线路参数,但没有考虑电网频率波动时由频谱泄露和栅栏效应导致相角数据误差偏大的现象。文献[7,8]提出了一种消除低频干扰的方法并分析了其对线路参数辨识的影响。文献[9]提出PMU实测数据相角误差较大,应避免直接应用。基于SCADA的线路参数辨识主要包括增广状态估计和量测残差灵敏度分析[10]。文献[11]提出针对所有量测量误差设置相同权重,忽略系统误差的影响。文献[12]提出基于多信息最小二乘算法进行线路参数辨识,但是受限于RTU测控单元的采样频率和传输模式的限制,一般SCADA信息4~5 s刷新一次,不能反映系统动态变化的特征。文献[13]采用综合赋权法辨识关键线路参数影响力指标,考虑了线路间传输信息以及线路最大容量考虑不足的问题。文献[14,15]提出了基于故障录波数据的输电线路参数计算方法,利用录波数据获取电压、电流相量值计算线路参数,但是相量值的计算受频率波动和暂态分量影响较大。
RTU与PMU所接模拟量一般是来自测量用电流互感器,主要为了保证稳态时的测量精度。故障时测量电流互感器易产生饱和,因此RTU/PMU所采集的信息不能反映电力系统故障时电压、电流的实际情况。故障录波器是电网故障或异常情况的“黑匣子”,采样频率可达到5~10 kHz以上,一般前接保护用电压、电流互感器,可反映真实的波形,但是存在数据不同步的问题,不能直接用于线路参数辨识[16,17]。因此,可以认为稳态时PMU的幅值数据精确度比较高,故障时故障录波数据精确度较高。
针对单一数据来源下线路参数辨识精度不高的问题,本文提出一种自适应融合多种数据源辨识线路参数的方法。该方法通过自适应提取故障录波数据的高频分量实现故障录波数据和 PMU数据的同步,通过同步后的故障录波数据的相角差修正PMU数据的相角差实现自适应数据融合,利用融合后的数据通过加权最小二乘实现线路参数的辨识,最终通过仿真和实测数据验证了本方法的有效性。
1 相角差误差对线路参数辨识的影响
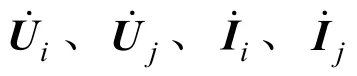
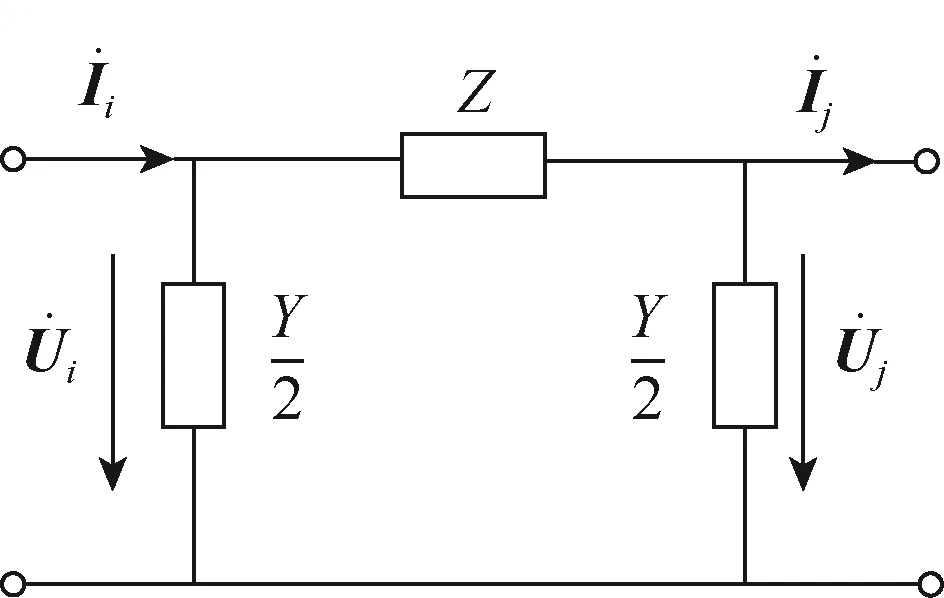
图1 输电线路π型等值电路Fig.1 π-type equivalent circuit of transmission line
目前,电网的相角主要通过基于DFT算法的PMU终端获得,然而电网的频率始终处于变化过程中,在任意时刻t,两侧由DFT算法计算出的PMU电压信号的同步相角差Δφuij理论值为:

式中:电压相角差由3部分构成,第一部分是线路两侧电压相角差准确值Δφuij0;第二部分是两测点频率偏移差Δƒij造成的误差;第三部分是 PMU中使用DFT算法计算的相角差误差ΔeφDij。
若已知线路电阻R、电抗值X以及线路末端电压幅值Uj、有功功率Pj和无功功率Qj,根据潮流关系可得到线路两端电压相角差为:
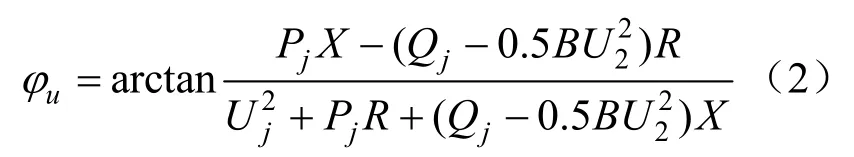
相角差对参数辨识的影响程度可以用线路参数对相角差的灵敏度来表示。为了方便对各个参数进行同一化分析,本文采用相对灵敏度计算方法,其计算函数为[18]:

设线路末端为参考节点,电压相角设为0,则参考节点下首端电压的相角φu即为相角差,则线路阻抗和导纳对电压相角差的灵敏度为:

则线路参数对电压相角差的灵敏度可表示为:
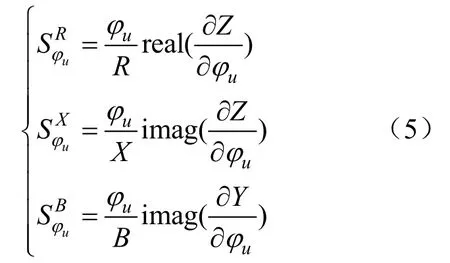
式中:real()、imag()分别表示相量的实部和虚部。
电压相角差变化范围为0°~10°时,线路电阻、电抗和电纳对电压相角差的灵敏度随相角差大小变化如图2所示。
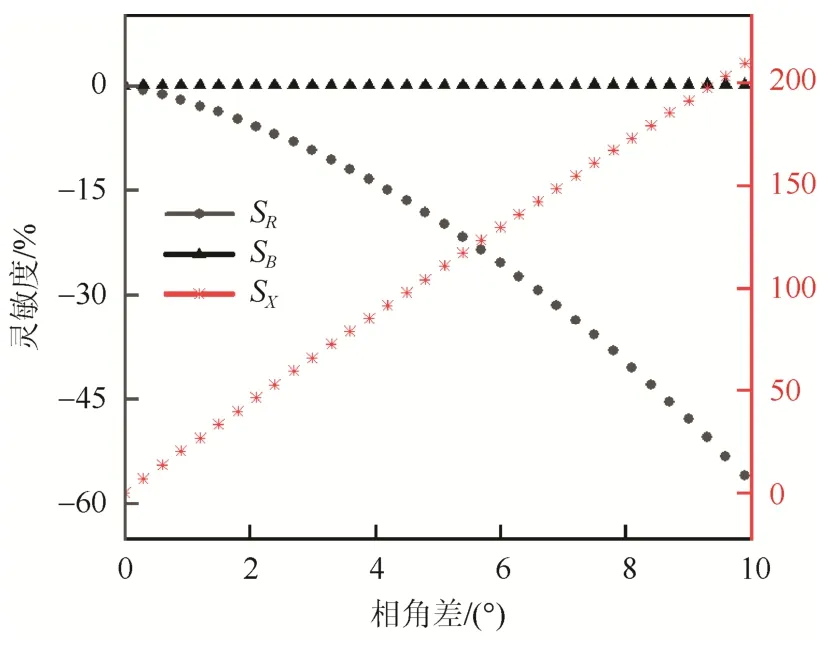
图2 灵敏度分析结果Fig.2 Results of sensitivity analysis
由图2可以看出电抗受到电压相角差影响最为明显,电纳几乎不受电压相角差的影响。当电压相角差为2.574 8°时,电压相角差出现0.01°误差,电抗辨识误差超过 56.4%,而电阻辨识误差为-7.6%,电纳辨识误差为 0.029%,因此相角差误差亟需校准。
2 录波数据修正PMU相角差数据
2.1 结合峭度因子的互补集合经验模态分解法
经验模态分解(empirical mode decomposition,EMD)方法是一种自适应信号处理方法,最显著的特点就是其克服了小波分析的基函数无自适应性的问题,可以将原始信号x(t)自适应分解为若干不同尺度相互独立的本征模态函数(IMF),但是出现间歇性信号时容易发生模态混叠现象。集合经验模态分解(EEMD)算法在EMD分解的基础上添加白噪声,从而使分解的IMF是单一模态,但重建之后的噪声残留较多,不可忽略。对此,CEEMD算法将原信号加上白噪声和原信号减去白噪声两个信号同时经过EMD分解,通过求取均值来抵消信号中加入的噪声[19,20]。具体算法流程如下:
(1)在原始信号x(t)中加入m对正负高斯白噪声,生成两组IMF:
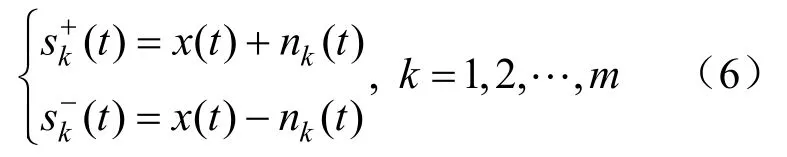
式中:x(t)为原始信号;nk(t)为加入的第k对高斯白噪声,由此可以得到2m个信号集合。
(2)对集合中每一个信号进行EMD分解,每个信号会生成一组预设个数的IMF分量,第p个信号的第q个IMF分量记为apq。
(3)将得到的2m个IMF分量进行平均处理,得到最终的IMF分量为:
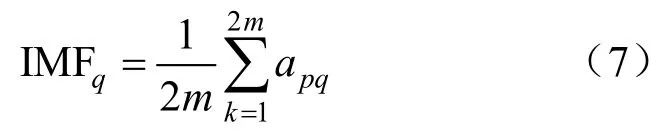
迭代停止条件一般是人为设定的IMF个数,所以一般情况下可以直接采用 IMF1分量作为高频分量,但实际研究发现,随着过渡电阻的增大,通过CEEMD算法得到的高频分量越不明显。以IEEE9节点系统仿真结果为例,设置以下情形:①过渡电阻为0.1 Ω;②过渡电阻为1 Ω;③过渡电阻为10 Ω。以情形①、情形②为例,各零序电流及相应的IMF分量(只选取前两个分量)如图3所示。
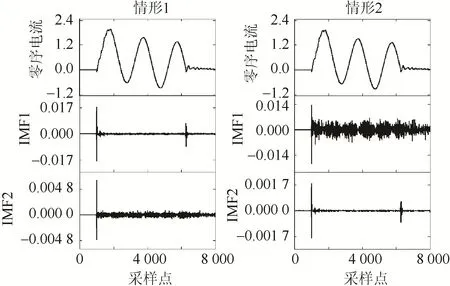
图3 情形①、②对比Fig.3 Comparison under cases ① and case ②
由图 3可以看出两种情形分解出的 IMF1和IMF2分量均含有高频分量,区别在于 IMF1分量包含的噪声过多,IMF2选为高频分量更为合适。为解决暂态高频分量选择的问题,本文提出基于峭度因子进行自适应选取暂态高频分量。峭度因子是表示波形平缓程度的,反映随机变量的分布。信号x的峭度因子计算公式为:
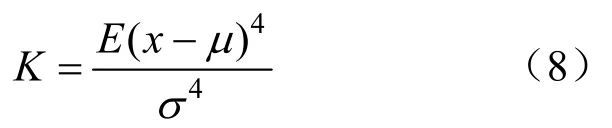
式中:μ为信号x的均值;σ为信号x的标准差;E(x)为信号x的期望值。
通过计算所有IMF分量峭度值,选择各峭度值最大的IMF分量作为高频暂态分量。3种情形下各分量峭度值如图4所示。
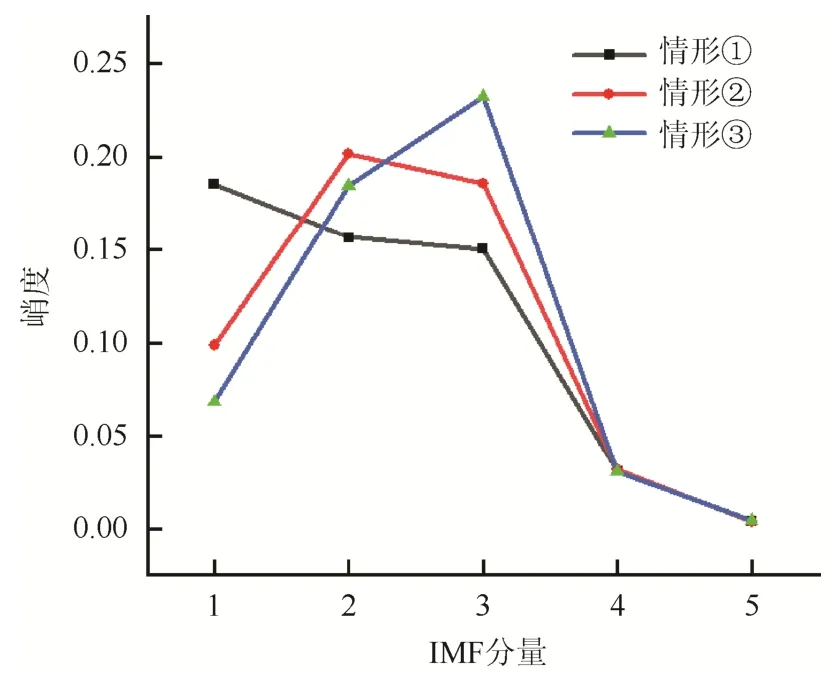
图4 3种情形峭度计算值Fig.4 Calculation of kurtosis under three cases
由图3、图4可以看出最大峭度值可以代表高频分量值,验证了通过峭度因子可以实现高频分量的自适应提取。
2.2 同步故障录波数据
故障录波器装置中有内部时钟,但内部晶振回路的时间偏差因设备的质量、使用寿命而异,因此线路两侧故障录波数据的时标并不相同,需要将线路两侧录波数据同步才可以直接使用。设置 IEEE9节点系统其中一回路发生单相接地故障,线路两侧零序电流经过自适应高频分量提取如图5所示。

图5 两侧零序电流高频分量Fig.5 High frequency component of zero sequence current on both sides
忽略行波在线路上的延时,利用高频信号峰值所对应的采样点计算两侧高频信号的延时点数量ΔX,由于两侧录波器采样频率ƒs已知,两侧故障录波器的延时为:

同步故障录波数据之后,由于故障录波数据时标不准确,无法直接与 PMU数据对比分析,同样可以选取故障时PMU电流的暂态特征量的时标给故障录波数据标注。通过自适应选取数据暂态特征量的方法可以实现故障录波数据的同步并准确标注时标,方便后续相角差数据的修正分析。
2.3 故障录波数据修正PMU相角差
线路发生短路故障时,故障录波器可以自动将故障前两个周波和故障后一段时长的数据上传至调度自动化中心。相比较利用固定采样频率的DFT算法计算出的相角差,独立计算出的两个稳态正弦波形的相角差更准确。同步并标记时标后首末端故障录波 A相电压信号如图 6所示。
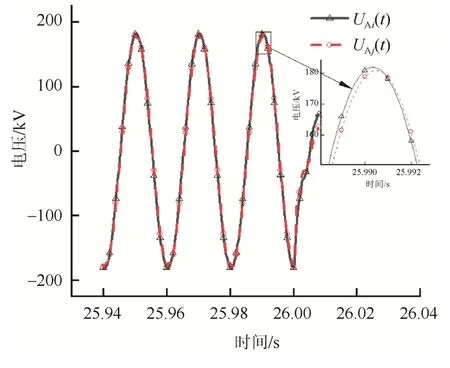
图6 校准同步后的两侧电压Fig.6 Voltage of both sides after calibration and synchronization
记故障发生前线路两侧的电压信号分别为Ui(t)=UiMsin(ωt+φui)、Uj(t)=UjMsin(ωt+φuj),根据相关函数的定义式,两侧电压信号自相关函数、互相关函数为:

当τ=0时,计算得两侧电压信号相角差为:
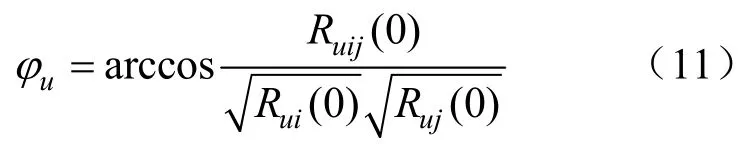
3 线路参数辨识模型
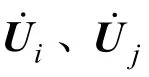
由测得的电气量构建输电线路潮流方程如下:
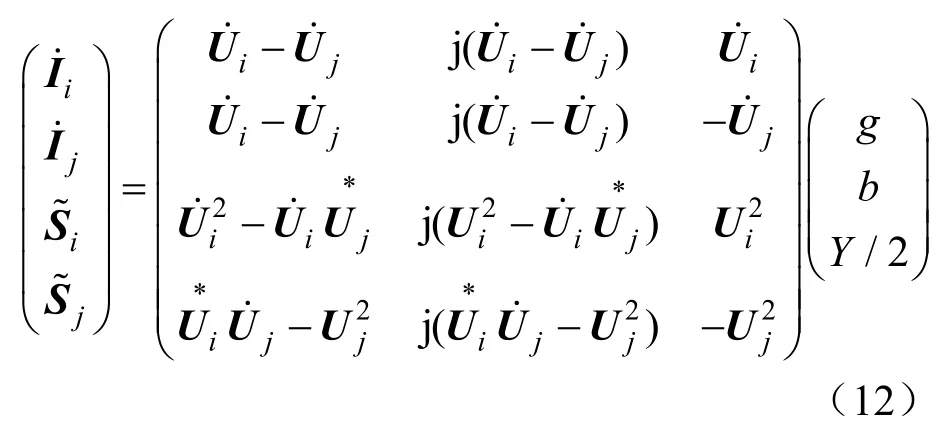
为增加辨识精度,将上式中的相量写成实部虚部,并写为偏差函数ƒi的形式,如式(13)~(20)所示。
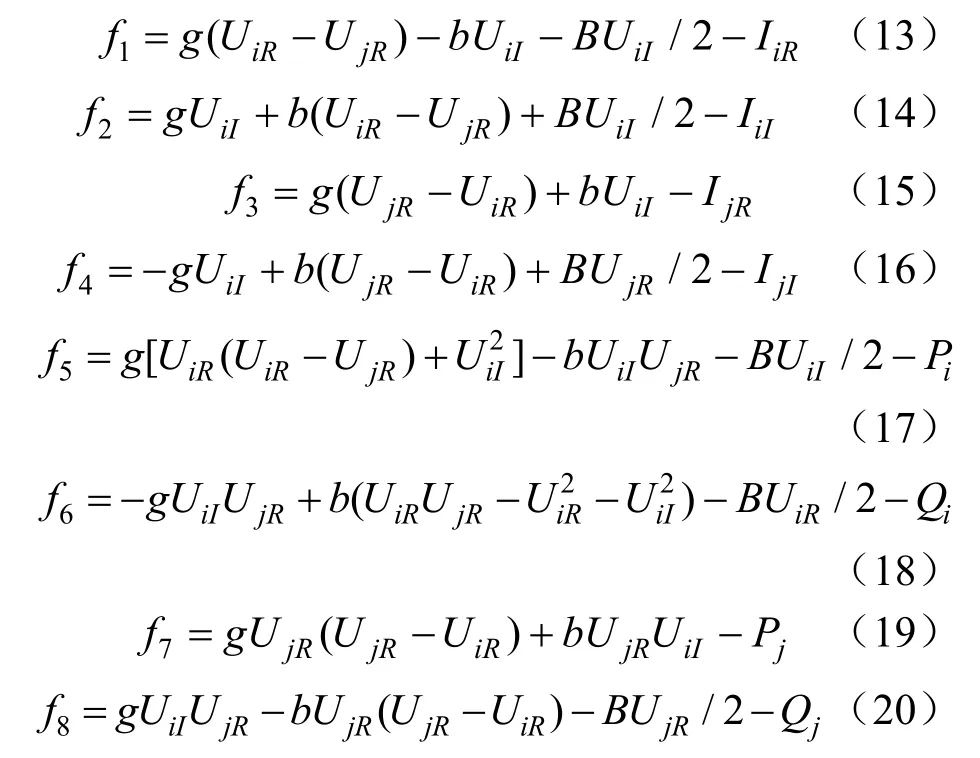
因此,量测数据包含误差的线路参数辨识问题可以转化为最小二乘优化来解决:
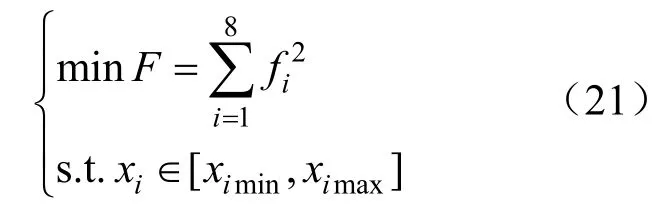
式中:F是关于辨识参数g、b和B的函数,通过迭代优化得到最终线路参数辨识解如式(22)所示。
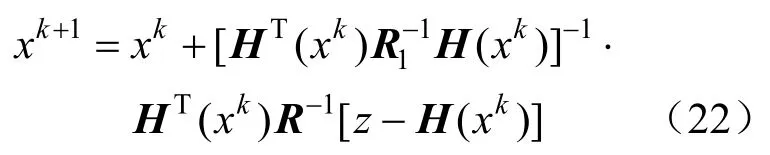
4 测试验证
4.1 仿真验证
在MATLAB/SIMULINK中搭建三机九节点系统,辨识其中一条220 kV线路参数。线路长度为50 km,正序参数为电阻R=0.899 3 Ω、电抗X=63.460 2 Ω、电容 C=0.373 5 μF。系统发生单相接地故障时采集线路两端电压、电流相量、有功和无功作为PMU量测量,并在仿真数据中添加高斯白噪声模拟实际数据,同时设置采样频率为5 kHz的故障录波器采集电压、电流波形数据。
由式(2)计算的线路两侧相角差潮流计算与PMU实测值如图7所示。
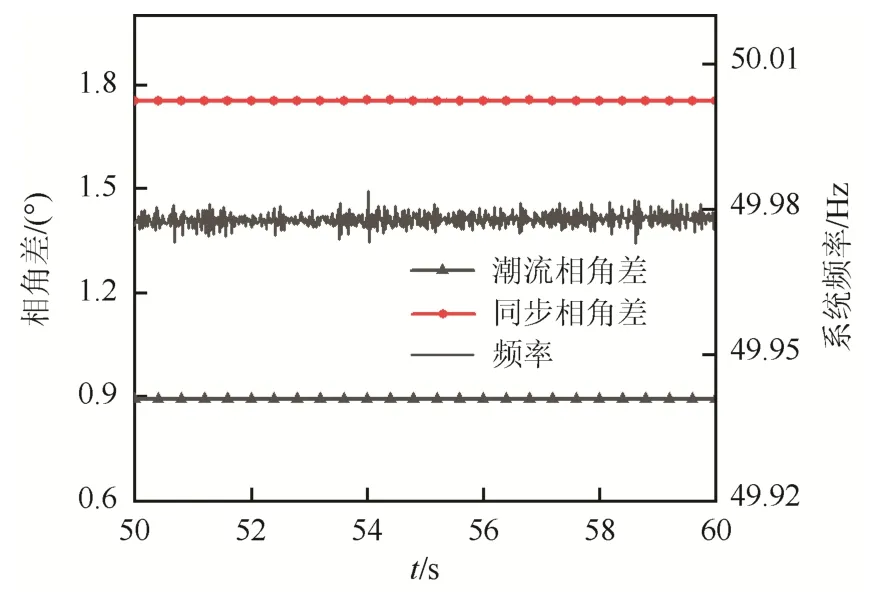
图7 相角差比较Fig.7 Comparison of phase difference
鉴于稳态时PMU数据的电压幅值、功率误差很小,认为由线路潮流计算出的相角为准确值,PMU相角差平均误差达到-49.16%。
人为设置两侧故障录波数据时延为0.1 s,在3种方案下实际计算延时和延时相对误差如表 1所示。由表1可以看出自适应峭度选取高频分量可以有效减小故障录波数据不同步问题,故障录波器采样频率在5 kHz时,数据同步精度最高可以达到0.2%。
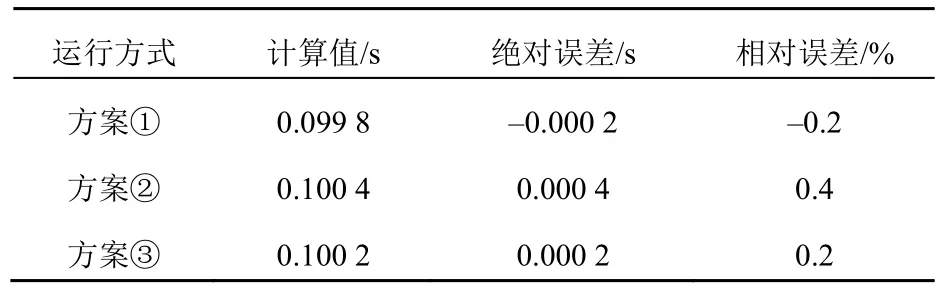
表1 3种情况数据同步结果Tab.1 Results of data synchronization under three cases
在同步两侧故障录波数据基础上,分别采用WLS算法和 AFD-WLS算法对线路参数进行辨识,辨识结果及误差如表 2所示。表 2表明AFD-WLS算法在线路参数辨识准确度更高,由于融合了故障录波数据的准确相角差,电抗辨识结果提升最为明显,与灵敏度分析结果一致。
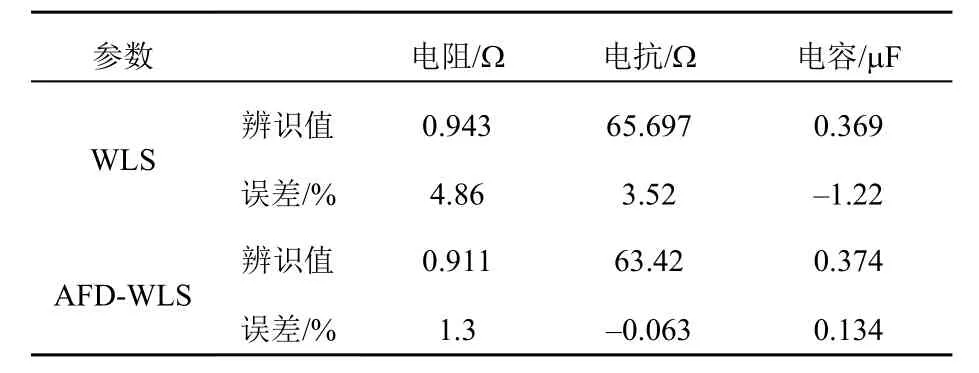
表2 两种算法的辨识结果比较Tab.2 Comparison of identification results of two algorithms
4.2 实测数据测试
选取青海电网日月山变电站和康城变电站一条长度为10 km的330 kV线路进行辨识,该线路两侧配有PMU装置、故障录波装置,离线值为电阻0.263 Ω、电抗2.18 Ω,电纳为8.8×10-5S。选取故障前两个周波数据进行同步修正后,利用融合数据辨识线路参数结果为电阻 0.32 Ω、电抗2.957 Ω,电纳为9.213×10-5S,用送端电压、电流数据和辨识结果计算受端电流波形,通过比较受端故障录波电流波形和基于辨识参数计算受端电流波形,校验参数辨识精度。波形复合误差记为:
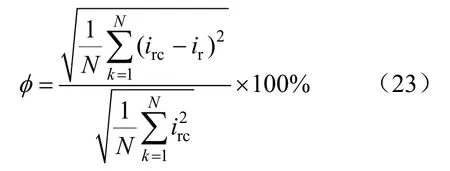
式中:irc为故障录波电流值;ir为基于辨识参数电流计算值。
辨识值、离线数据拟合受端波形与实际录波受端波形如图8所示。

图8 拟合波形与实际波形对比Fig.8 Comparison of fitting waveform and actual waveform
由图8可见,基于辨识参数拟合受端电流波形效果最好,波形复合误差为 0.39%,离线参数拟合波形复合误差为2.43%,说明基于自适应融合数据下线路参数辨识值更加准确。
5 结论
针对辨识线路参数使用单一数据源数据精度不足的问题,本文采用了一种基于加权最小二乘的自适应融合多种数据源辨识线路参数的方法,并在仿真和实测数据进行了应用,辨识结果表明本文方法辨识精度明显高于普通加权最小二乘法,验证了本方法的有效性。相比较普通加权最小二乘算法,本文方法有以下优点:
(1)利用软件算法可实现录波器时钟延时自适应校正,不需要额外设备;
(2)自适应融合数据可有效提高数据质量,提高线路参数辨识准确度,其中电抗参数尤为明显;
(3)充分利用了系统运行数据,提高了故障录波数据的应用价值。
