可重复使用运载器预测制导与鲁棒容错控制

2021-07-01都延丽林海兵王玉惠

哈尔滨工业大学学报 2021年6期

都延丽，林海兵，刘武，王玉惠

(1.南京航空航天大学航天学院，南京 211106；2.南京航空航天大学自动化学院，南京 211106)

可重复使用运载器(Reusable launch vehicles, RLV)的再入制导与控制一直以来是各国研究的重点. RLV飞行包线大、再入环境复杂、约束苛刻、非线性与不确定特征强，同时，再入段大气较为稀薄，气动舵面更易发生饱和、部分失效等故障，这都为制导与控制系统的设计带来极大挑战[1]. 因此，有必要研究能够抑制不确定/干扰、舵面失效及饱和影响的具备较强鲁棒性能的容错控制策略，并引导RLV在满足再入约束的条件下到达目标位置，这对于再入飞行任务的成功来说至关重要.

针对RLV的制导律设计问题，数值预测校正制导对初始误差不敏感，落点精度较高，鲁棒性较好，目前越来越受到关注[2].Lu[3]针对不同升阻比的再入飞行器，提出统一的预测校正制导算法，但计算量较大. Xue等[4]用准平衡滑翔条件(Quasi-equilibrium glide condition，QEGC)将再入过程约束转换为倾侧角幅值约束，但在QEGC飞行特性降低的情况下，难以保证过载不突破限制. 张鹏等[5]将哥氏加速度引入QEGC并设计二次函数倾侧角幅值模型，在满足过程约束条件下以提高再入制导精度和鲁棒性. 针对RLV的不确定性/干扰下的控制问题，Wang等[6]在反步法中引入鲁棒自适应律来估计未知不确定的上界. Hu等[7]通过自适应模糊逼近和动态面控制方法来减小不确定性的影响，但学习参数较多将影响实时性. 对于舵面失效及饱和的飞行器容错控制问题，鲁棒、自适应和观测器方法仍是较为有效的手段. 于彦波等[8]针对航天器执行器故障和控制受限问题设计了基于积分滑模面的自适应姿态容错控制律来提高系统的鲁棒性能.Lee等[9]等使用自适应线性未知输入观测器进行模型匹配，虽然可以有效抑制扰动且能处理系统中的未知非线性和舵面故障，但飞行器模型的线性化过程中存在一定的失真.

综上所述，国内外学者对于RLV再入制导律和姿态控制器的研究通常是两个相对独立的领域. 然而在实际飞行中，制导系统与姿控系统须进行整合以形成完整的六自由度再入系统，才能检验飞行器能否完成再入任务，满足要求的制导精度. 由于目前公开的RLV和高超声速飞行器气动资料较少，缺乏包含大攻角以及完整横侧向气动参数的飞行器模型[10]，故该方面验证结果较少. Tian等[11]同时考虑制导环和姿态环，采用伪谱法进行制导律设计并利用二阶滑模控制器和干扰观测器对制导指令进行跟踪. Qian等[12]采用预测制导法生成标称轨迹，将轨迹指令输入到姿态环，应用反步法实现了飞行器的姿态控制. 严晗[13]针对导弹控制系统，直接进行制导控制一体化设计，但RLV的再入飞行存在强非线性特性，且受到各种约束的限制，姿态控制相比导弹更加复杂，直接进行制导与姿态一体化控制设计的难度极大.

HORUS-2B飞行器[14]是近年来公开数据的一种RLV模型，它具备完整的纵横向气动参数数据，迎角范围为0°～45°，马赫数在1.2～20.0之间，完全能够开展再入段制导与控制研究.本文针对该飞行器，设计了约束预测校正制导律，对于姿态系统中的不确定/干扰、作动器部分失效及饱和问题，提出了改进跟踪微分干扰观测器(Improved tracking differential disturbance observer,ITDDO)来估计不确定/干扰及舵面部分失效作用，并设计辅助抗饱和系统来解决舵面饱和问题. 之后，对上述制导与控制方法进行了六自由度联合仿真.实验结果表明该方法能够引导RLV在满足再入约束的条件下到达终端落点区域，并具备良好的鲁棒容错控制性能.

1 问题描述

考虑圆球形大地和地球自转的情况，RLV经量纲一的转化后以能量e为自变量的三自由度制导方程以及姿态系统方程[11]如下：

(1)

(2)

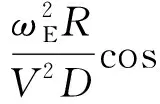
(3)

(4)

(5)

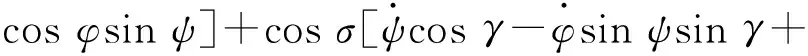
(6)

sinφsinγ),

(7)

(8)

(9)

(10)

为方便设计非线性姿态控制律并考虑不确定/干扰和作动器失效，可将姿态系统方程式(5)～式(10)转化为如下仿射非线性方程组：

(11)

为保证RLV成功完成再入飞行任务，再入轨迹必须满足热流密度、过载和动压3个硬约束条件[3]：

(12)

(13)

(14)

本文的主要目的为设计六自由度制导控制系统及鲁棒容错控制律，以引导HORUS飞行器从再入初始状态到末端能量管理段的飞行，在考虑姿态不确定/干扰、舵面部分失效及饱和的影响下实现飞行器鲁棒容错控制，并满足再入任务要求.

2 制导控制系统总体设计

RLV制导控制系统如图1所示，该系统整合了制导环与姿控环. 在六自由度仿真中，姿控系统的参考输入量Ωr=[αrβrσr]T由制导环的改进预测校正制导算法在线生成. 本文提出一种鲁棒容错控制方法来设计姿态控制器，用以跟踪制导环计算的指令. 需要说明的是在制导系统当中，部分状态变量是量纲一的，故当实际飞行状态量传入到制导系统当中时，须经过归一化处理[3].

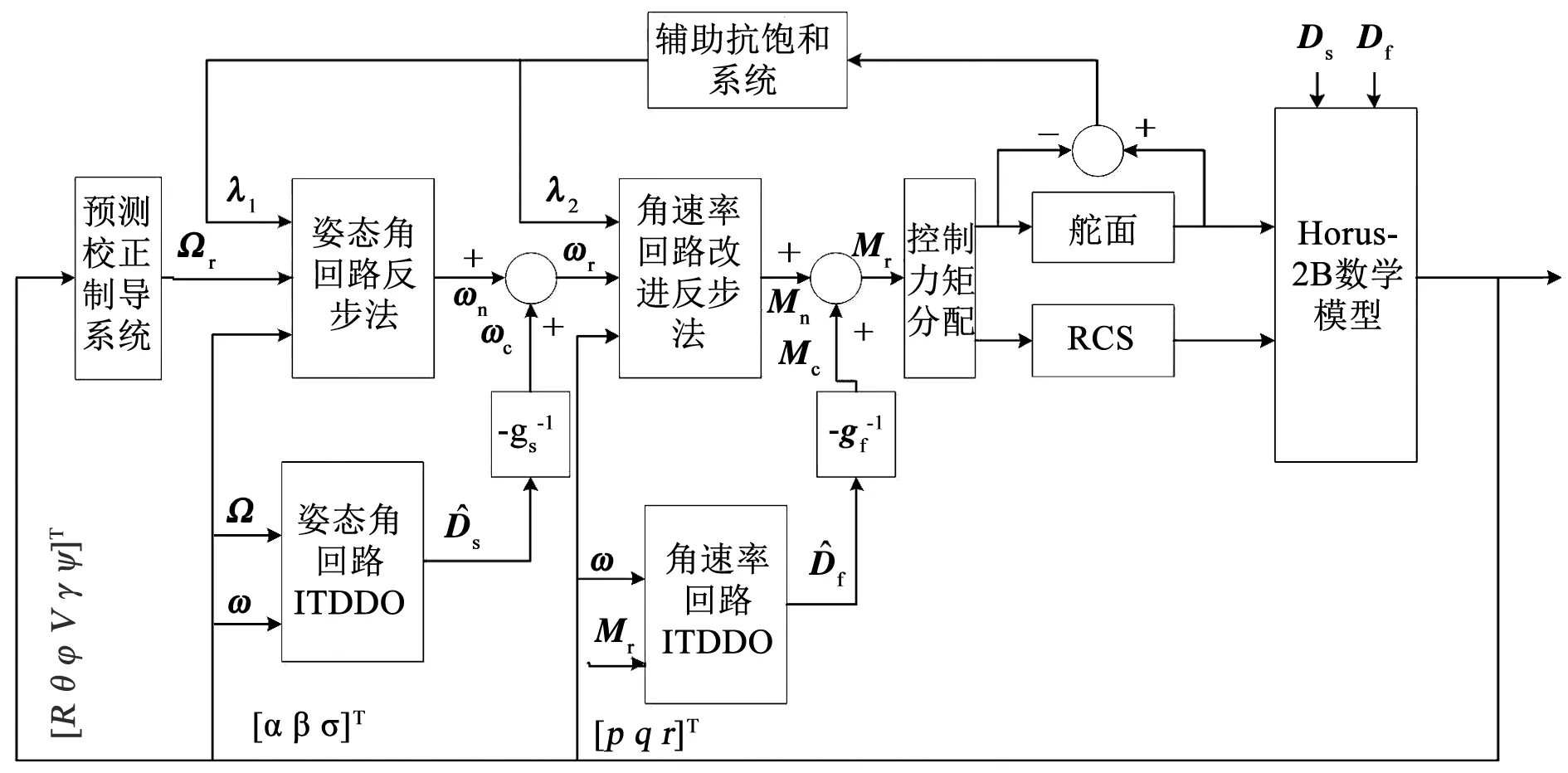
图1 联合制导控制系统

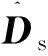
3 六自由度制导控制系统设计

3.1 改进预测校正制导律设计

根据大气指数模型ρ=ρ0eah3+bh2+ch+d(ρ0、a、b、c和d是已知参数)可知，ρ仅是关于高度h(等于R减地球半径)的函数. 因此，式(12)～式(14)能够进一步转换为关于高度h和速度V的不等式，根据此不等式可以确定RLV在高度-速度空间内的再入走廊下边界(如图4虚线所示).

依据文献[5]提出的约束预测校正制导方法，RLV的迎角α按照事先确定的标称迎角剖面来变化，飞行器纵向运动采用倾侧角幅值|σ|来控制，侧向运动采用倾侧角符号sgn(σ)控制. 设计中采用二次函数参数化模型[5]来对倾侧角幅值剖面进行参数化设计. 与常规线性参数化模型相比，该模型得到的再入轨迹更加平滑，再入过程中的热流密度和过载更小. 另外，在QEGC条件中还引入哥氏加速度的影响，从而将高度-速度再入走廊转换为倾侧角幅值约束.α与σ代入式(1)～式(4)的制导方程，积分后得到RLV的预测落点. 当预测落点与期望落点之间存在偏差时，返回重新校正初始设计的倾侧角幅值参数化模型，直至预测与期望落点间的偏差满足要求. 一个周期内的再入飞行制导流程如图2所示，其中sf为飞行器的待飞航程.

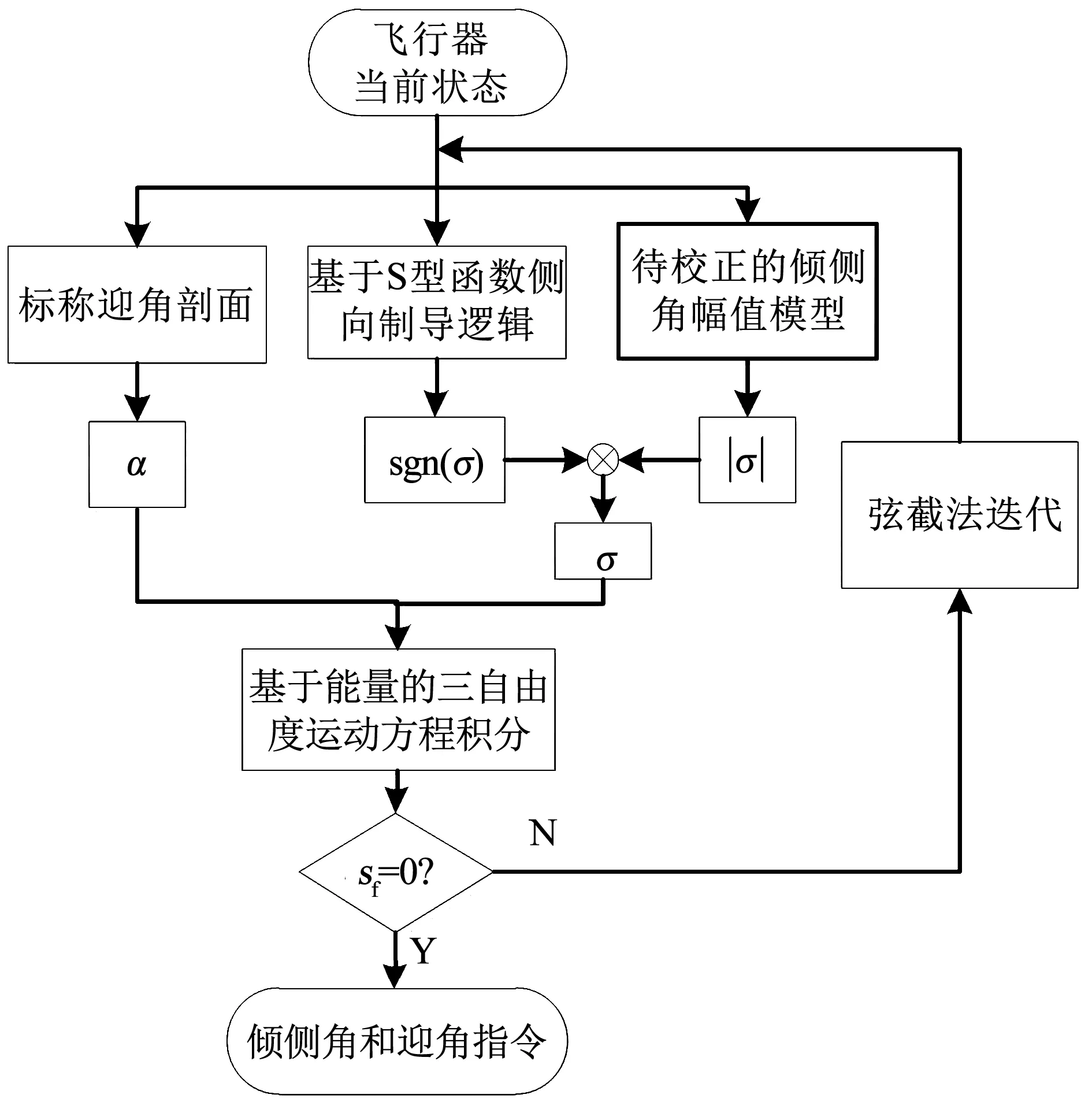
图2 改进预测校正制导流程

然而，文献[5]中的侧向制导逻辑中将航向角偏差走廊分成多段来进行设计. 此方法在编程实现时较为繁琐，本文采用S型函数来进行设计，将其中的再入走廊简化成如下所示的两个阶段：

(15)

式中：|Δψth|为ψ与视场角(飞行器当前位置与目标位置间的夹角)之差的阈值.

3.2 改进跟踪微分干扰观测器的设计

为提高控制系统的鲁棒性并对舵面部分失效进行容错控制，本文针对不确定仿射非线性方程描述的MIMO系统，借鉴文献[15]提出了一种ITDDO，系统如下式所示，观测器形式如定理1所述.

(16)

式中：x为可测状态量；u为系统控制量；x0为状态初值；D为有界的未知复合干扰，包括模型不确定、外界干扰及舵面部分失效作用.

定理1针对如式(16)所表达的MIMO系统，设计如下式的ITDDO.

(17)

f(z1,z2)=-a1[z1+|z1|p/qarctan(b1·z1)]-

a2[z2+|z2|p/qarctan(b2·z2)],

(18)

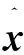
引理1[16]假设平衡点为(0,0)的系统(19)全局渐进稳定，系统给定初始值为z1(0)=z10和z2(0)=z20.

(19)

(20)

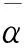
(21)

其中

(22)

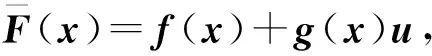
(23)

(24)

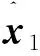
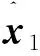
定理1得证.

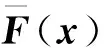
根据姿态方程式(11)和设计ITDDO的式(17)、(18)，有姿态角和角速率回路的ITDDO形式如下：

(25)

(26)

3.3 鲁棒容错姿态控制器设计

姿态系统的非线性控制律基于反步法进行设计. 定义姿态角跟踪误差和角速率误差为：

es=Ω-Ωr,

(27)

ef=ω-ωr.

(28)

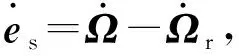
(29)

根据式(29)设计姿态角回路控制律ωr如下：

(30)

在不考虑舵面饱和的情况下，可将式(11)中的舵面失效合并至复合干扰当中，即Df2=Df-gfE·Md,于是角速率回路改写成如下形式：

(31)

式中Mr=MRCS+Md，这里将舵面部分失效时未能提供的力矩视为角速率回路中不确定项的组成部分. 在不考虑饱和时，将式(28)微分后可得

(32)

设计控制力矩指令Mr如下[18]:

(33)

为进一步加强控制器的鲁棒性能，向式(33)中引入改进sigmoid函数构成的饱和项：

(34)

式中：e为自然常数，ε>0为调节因子，因此可得实际控制量为

Kcsat(x)),

(35)

针对RLV再入过程中的舵面饱和问题，假设饱和前、后的力矩差值为Δδ=sat(M)-Mr，且‖Δδ‖≤M，‖·‖为L2范数，M为正常数，则角速率回路方程式(31)中的Mr应由实际力矩sat(M)代替.本文借鉴文献[19]设计了一种抗舵面饱和辅助系统:

(36)

式中：c1和c2为待整定的对角矩阵，λ1和λ2为辅助系统中的状态向量. 因此，当前系统的姿态角和角速率误差为

(37)

将上式取微分，代入式(28)、(29)、(32)、(36)和(37)，可得:

(38a)

(38b)

注意式(32)中的Mr已由sat(M)代替.

设计姿态角控制律和角速率控制律如下：

(39a)

c2λ2+Kcsat(-zf/ε)).

(39b)

3.4 稳定性分析

定理2针对RLV的姿态控制系统，采用式(17)的ITDDO、式(36)的辅助抗饱和系统和式(39)的姿态控制律，闭环系统局部一致渐进有界.

将式(39a)代入式(38a)，可得

(40)

(41)

定义角速率回路李雅普诺夫函数为

(42)

将式(42)微分并代入式(38a)和式(41)可得

(43)

(44)

(45)

可知，V2≤V，将式(45)微分可得

(46)

将式(41)展开可得

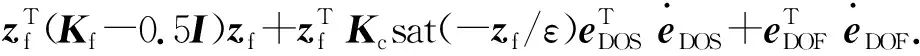
(47)

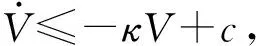
(48)

式(48)的两边同乘以e-κt，且在[0,t]上积分可得

(49)

因此

(50)

当系数κ>0时，下式成立:

(51)

假设辅助系统状态向量的范数‖λ1‖有界，则构造如下Lyapunov函数:

(52)

式(52)微分后得到：

(53)

其中

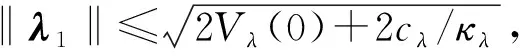
(54)

因此，通过选取合适的系数值，可以使误差收敛到任意小. 定理2证毕.

4 仿真验证

表1 初始状态量和末端状态量

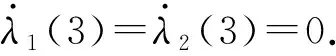
首先，仅针对姿控系统实验了ITDDO对于复合干扰的学习能力，仿真时间为100 s，采样周期为20 ms.施加复合干扰模拟函数如下：

(55)

(56)

如图3所示，ITDDO与文献[17]的方法以及非线性干扰观测器(NDO)进行了比较. 由于姿态角回路处在角速率回路的外环，其干扰学习效果更优，故仅针对角速率回路通过叠加所有采样点的误差平方和来进行3种方法的比较. 可以看出，ITDDO三通道干扰估计的误差平方和最小，同时3个姿态角的控制误差平方和也达到了最小.

图3 姿态控制器误差评价

然后，将ITDDO结合定理2中的方法，应用到了制导与控制系统联合仿真当中. 复合干扰仍按式(55)、(56)的形式. 另外，在400～850 s时，设左升降副翼舵发生部分失效，失效因子为0.3，850～1 000 s时，右升降副翼舵发生部分失效，失效因子为0.2. 为验证方法的有效性，分4种情景进行仿真：case1包含ITDDO、反步法和抗饱和辅助系统；case2包含ITDDO、改进的反步法和抗饱和辅助系统；case3包含NDO、改进反步法和抗饱和辅助系统；case4只包含了ITDDO和改进反步法. 图4、5显示出飞行器质点的位置变化，可以看出所有情景下飞行器都能满足制导控制要求，使终端落点到达允许的误差圆范围内(半径10 km)，同时也满足再入过程约束的要求(见式(12)～(14)). 然而，case2和case3的精度略高于case1.

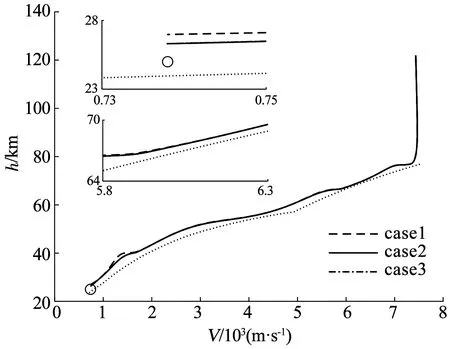
图4 高度速度剖面

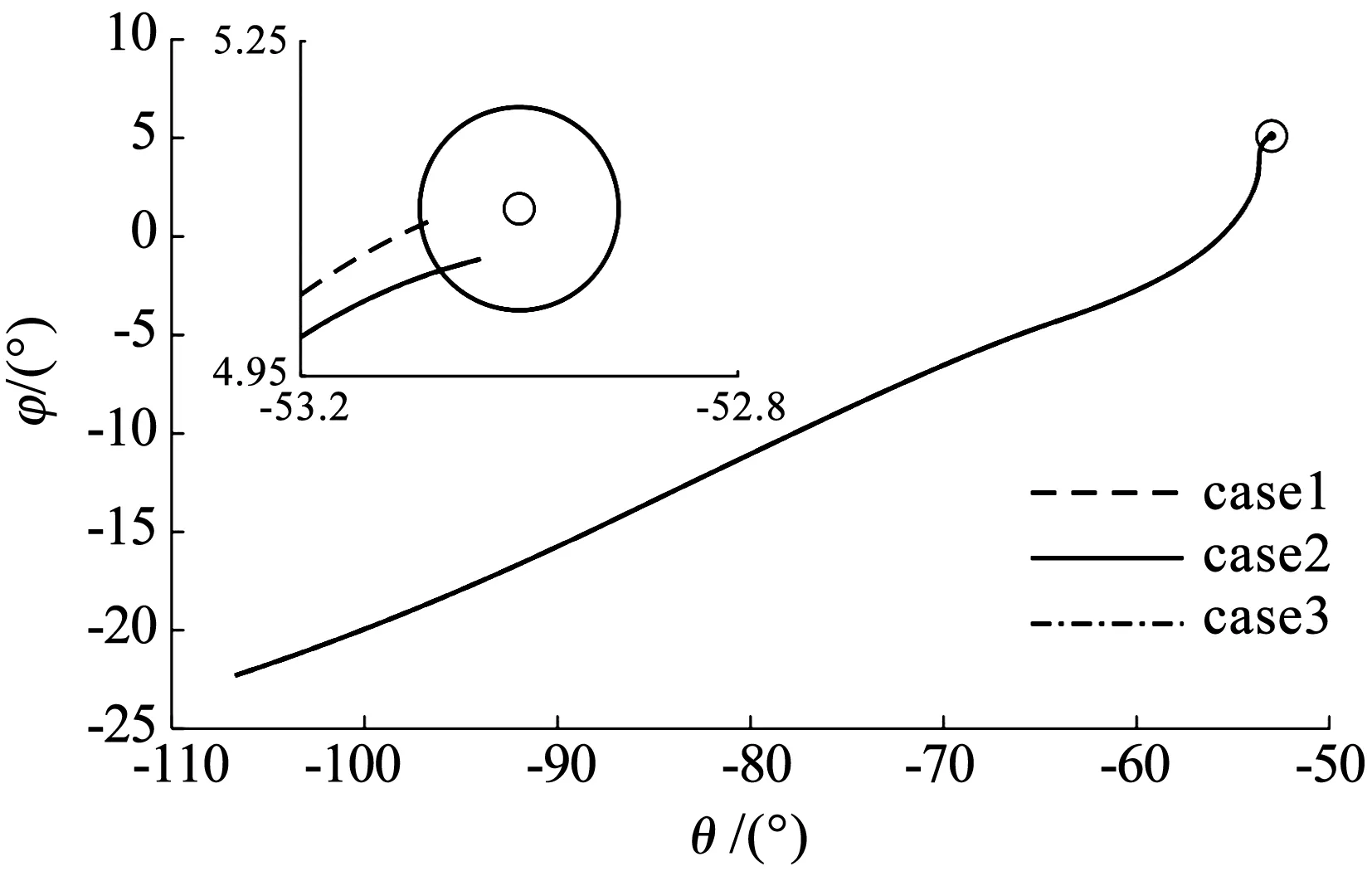
图5 地面轨迹图

图6、7为迎角和倾侧角的跟踪效果. 再入过程中控制侧滑角为零，因篇幅限制，故略去该图. 虽然这3种情景中产生的参考姿态角因在线预测制导(虚线)而不完全重合，但是此细微差别并不影响实验的结果，故只选择了一条轨迹作为参照. 从图6、7可知，当倾侧角每次发生翻转时，3种情景中的姿态角存在较大震荡. 为了更清楚地描述这种情况，图6中分别附有700～750 s和1 255～1 270 s的局部放大图. 从放大图中可知，在720 s处，攻角的波动幅度大幅增加，这是因为在倾侧角翻转的过程中需要更多的控制力矩来保证系统的平稳运行. 此时，由于舵面发生饱和及角速率回路输出限幅这两个原因，无法提供所需控制力矩而导致姿态角暂时偏离参考值. 改进反步法的姿态角跟踪精度有了显著的提升，从图7的1 095～1 100 s的局部放大区间也可以看出改进的反步法能够使跟踪性能得到显著的增强. 而case4中的辅助抗饱和系统对控制效果的改善作用也较为明显.

图6 迎角跟踪结果

图7 倾侧角跟踪结果

在图6、7中，每当倾侧角翻转前后，姿态角的跟踪就会发生震荡，它们出现的时间点和控制舵面发生饱和的时间点一致. 由于左升降副翼舵和右升降副翼舵在670～750 s和1 080～1 140 s这两个区间发生比较严重的饱和，故图8、9给出了这两个区间舵面的偏转情况.

图8 左升降副翼舵偏转

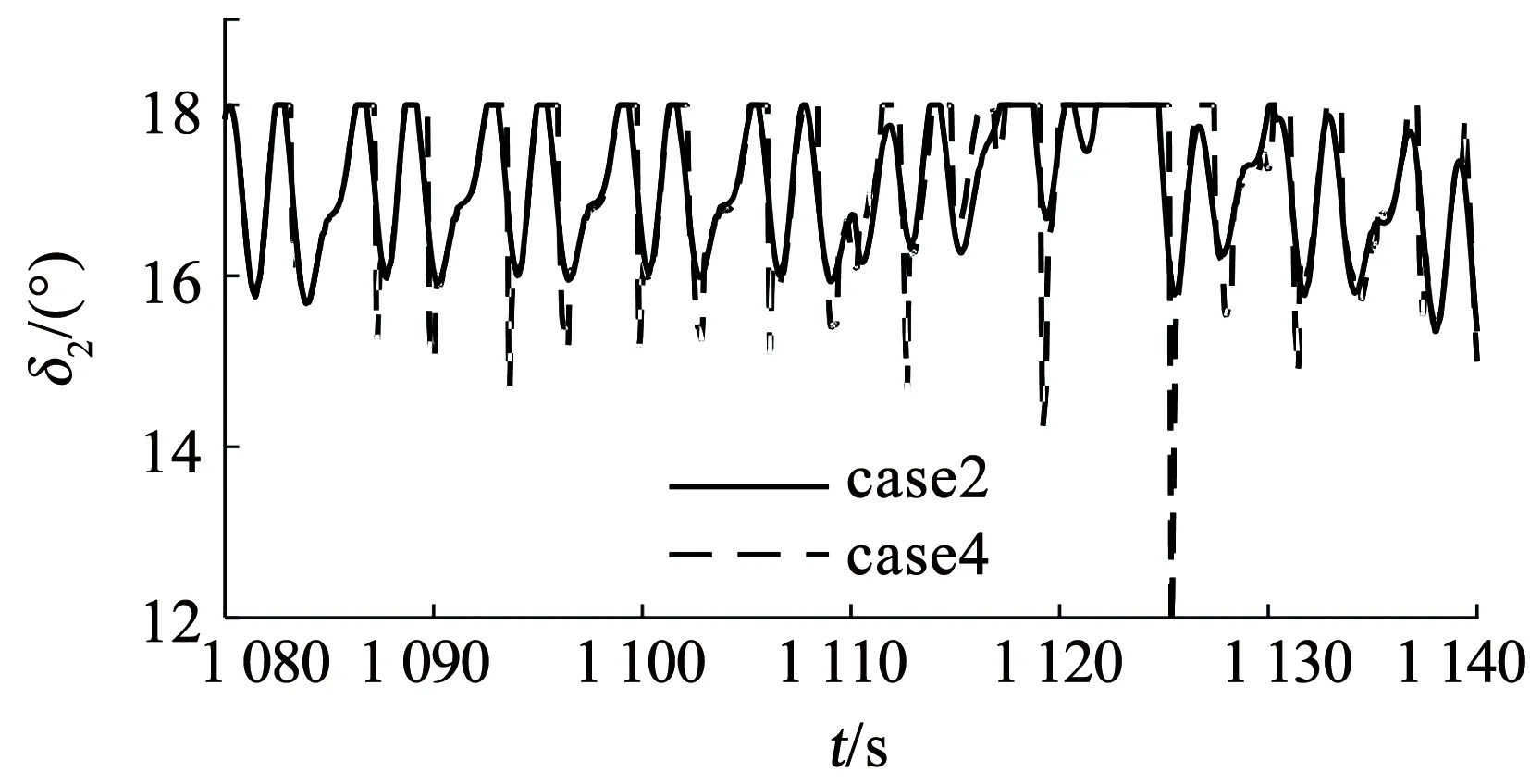
图9 右升降副翼舵偏转

从图8、9可知，辅助抗饱和系统可以使舵面尽快离开饱和状态，这样有利于改善舵面饱和时引起的控制系统性能下降或系统无法运行的情况. 由于篇幅限制，本文只显示了攻角的干扰估计和滚转通道的干扰估计效果. 从图10可以看出，在制导与控制的联合系统中，case2中的ITDDO比case3中的普通NDO具有更好的复合干扰估计效果. 从图11可知，ITDDO也具有更好的响应能力.