基于系统性风险角度的基金资产配置策略分析

孙晨阳，汪雪琪，王雪

基于系统性风险角度的基金资产配置策略分析

孙晨阳1，汪雪琪1，王雪2

（1.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030；2.安徽财经大学 经济学院，安徽 蚌埠 233030）

：为从系统性风险角度分析基金资产配置策略，首先利用ARMA模型预测股票价格，并构建线性规划模型确立最优的股票投资组合策略。其次综合考虑每家公司配置资产时的收益和风险，构建马科维茨投资组合模型和投资效用-VaR平衡模型，给出最优投资组合策略下的投资效用以及风险价值。最后建立了基于聚类分析的相似性度量模型分析其公司间资产配置的相似性。

ARMA；马科维茨；VaR；聚类分析；相似性

公募基金是以证券为主要投资对象的一种公开向社会大众募集资金的证券投资基金，具有筹集潜力大的特点。但其收益的同时也面临着系统性风险。因此，如何均衡基金投资收益和系统性风险的关系至关重要。

为此，本文针对资产管理业务，结合样本股票交易数据进行分析，在给出拟合预测数据的基础上，综合考虑投资效用和风险价值，为公司提供最优的投资策略。并针对股票公司一年的投资数据来分析他们资产配置策略的相似性，为公司在资产配置组合上提供相关建议，并通过公司现有的盈利数据给其他股民和公司带来配置资产方面的参考意义。

1 数据来源与假设

本文所运用到的数据是经过网络搜集与爬虫找到的2019年10家公募基金公司在股市中的一部分资产配置信息，以及寻找了2019年样本股票价格数据。该文的研究过程和结论均建立在假设的基础上（1）假设以所有基金的持股市值总和作为初始财富，以投资效用最大化为目标。（2）不考虑股票之间的相关性且不考虑卖空。（3）假设2020年所有基金公司仍然按照2019年的资产配置策略进行投资。

2 基于ARMA模型的效用最大化分析

2.1 研究思路

在不考虑风险的情况下，以投资效用最大化为目标确定最优的股票投资组合策略。对此，首先通过每只股票价格数据，利用ARMA[1]模型预测出下一年各股票的价格，进而计算各个股票的月收益率和平均月收益率。最后再利用预测出的每只股票的收益率构建单目标线性规划模型来确定最优的股票投资组合策略，以投资效用最大化为目标，投资总额不超过初始财富，且最多投资不超过只股票为约束条件，通过线性规划模型得到最优的股票投资组合策略。

2.2 研究方法

构建如下ARMA（,）[2]模型来预测下一年各股票的价格：

通过上述模型，预测出下一年各股票的价格，进而计算各个股票的月收益率，并将平均月收益率进行比较，找到较大的前只股票，当不考虑投资风险时，通过每只股票的收益率构建如下效用最大化线性规划模型来确定最优的股票投资组合策略：

2.3 结果分析

对2020年样本股票的所有开盘日进行预测，并将其中一只股票趋于稳定的收益率如图1所示。

图1 2020年股票一走势预测图

经过LINGO运行线性规划模型得到如下结果，可知每个公司均将资产投给股票47时，投资效用最大，具体结果如表1所示。

表1 各公司最优投资组合

在固定初始财富的限定条件下，假设每家公司初始打算投资10只股票，经计算每家公司仅投资一只股票时投资效用最大，且均投资股票47，当每家公司投资股票47的权重为{0.045, 0.054, 0.060, 0.073, 0.097, 0.052, 0.119, 0.200, 0.123, 0.178}时，在满足投资效用最大化的同时，确立出了最优的股票投资组合策略。

3 基于马科维茨理论的VaR分析

3.1 研究思路

根据样本数据，度量并排序每个基金公司2020年95%置信水平下的风险价值。对此，主要利用ARMA模型预测出的每只股票的收益率，综合考虑每家公司资产配置策略的收益以及风险，通过构建马科维茨投资组合模型，得出各公司投资的10只股票的协方差矩阵，进而得到10只股票的最优权重。通过预测出每家公司投资的股票交易数据以及各自所占权重计算出投资组合的收益率，进而得到每个基金公司2020年95%置信水平下的VaR，即风险价值，并对10家公司的风险价值进行排序。

3.2 研究方法

假设2020年所有的基金公司仍然按照2019年的资产配置策略进行投资，根据ARMA模型得到的每只股票的收益率，在考虑了风险因素之后，为了在效用一定时保持投资组合的最低风险，构建如下马科维茨投资组合模型[3]：

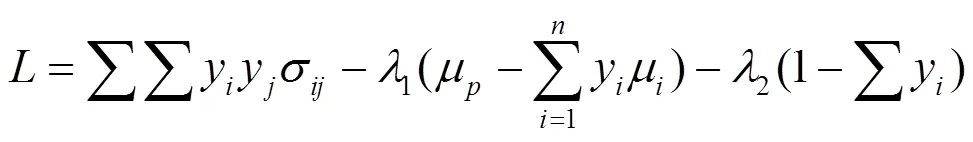
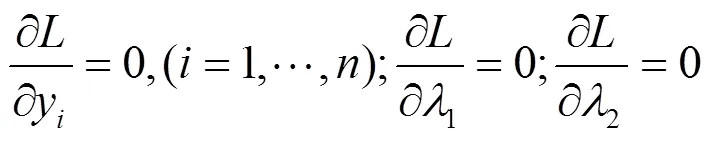
3.3 结果分析

通过历史模拟方法来估计VaR，根据每家公司10只股票的交易数据及其权重，计算投资组合的收益率，通过投资组合的收益率分别计算并比较10家公司在95%置信水平下的VaR的值，依次将10家公司按照VaR值进行排序，即VaR值越大，其对应的风险越大，风险价值越大。将每家公司的投资组合的收益率按照从小到大的顺序排序，排序后如表2所示。

表2 各公司从低到高投资组合收益率

在95%置信水平下对每家公司12个收益率排序来估计VaR值：

12*(1-95%) = 0.6≈1 (9)

则按从小到大投资组合的第一个收益率即为VaR值，即VaR(A)=-0.059303118, VaR(B)=-0.059596820, VaR(C)=-0.046937852, VaR(D)=-0.056705819,VaR(E)=-0.070521306, VaR(F)=-0.065477704, VaR(G)=-0.014423933, VaR(H)=-0.054831021, VaR(I)=-0.046565945, VaR(J)=-0.069337861。

表3 各公司VaR排序

其中，VaR(A)=-0.059303118代表1000万按10只股票的权重进行投资，一天内有95%的把握会亏损不会超过59.303118万，其他各公司含义类似。可知，当VaR的绝对值越大，代表风险价值越大，则将各公司风险价值进行排序，如表3所示。具体分析可知，风险价值最大的为E公司，其VaR(E)=-0.070521306，最小的为G公司，其VaR(G)=-0.014423933。

4 基于马科维茨理论的效用-VaR分析

4.1 研究思路

为了兼顾效用和风险确定最佳的股票投资组合策略，根据马科维茨均值-方差[4]构造效用-VaR平衡模型来确定最优的股票投资组合策略，通过赋予效用最大化为目标和风险价值为目标各1/2的权重，计算出最佳的投资组合策略。

4.2 研究方法

如果要求2020年整个系统既能保证投资效用最大化，同时又能使风险价值最低，构建如下效用-VaR平衡模型：

4.3 结果分析

根据建立的投资效用-VaR平衡模型得到：

N(A)=102502.8638, N(B)=125127.9448, N(C)=136847.9847, N(D)=166731.5202, N(E)=222687.1263, N(F)=118527.7751, N(G)=272949.5588, N(H)=458844.8519, N(I)=283586.4893, N(J)=408678.5679。

根据模型的建立以及求解的结果，可知平衡程度最大的是H公司，则其资产配置即为最优，分别投资股票47, 12, 14, 49, 11, 13, 50, 33, 51, 52, 17的权重为{0.5, 0.084853896, 0.123244297, 0.102203449, 0.048585886, 0, 0.0587684, 0, 0.028800526, 0.025588762, 0.027954786}。

针对上述分析，可知当达到最优股票投资组合策略时，投资效用为

风险价值为

VaR=VaR(H)=-0.054831021 (12)

可知，当公司在投资效用为0.099，风险价值为-0.055时，公司的投资组合方可达到最优。

5 基于聚类分析的相似性研究

5.1 研究思路

利用10家公司资产配置信息的样本数据，从而来度量不同基金公司之间的资产配置策略的相似性。首先，本文将各公司持有的每只股票市值与公司持股总市值的比率作为向量（未持有即为0），通过层次聚类分析，运用MATLAB软件计算，构建了10家公司个体间欧氏距离的相似矩阵，并观察相似矩阵以及聚类结果，寻找两家基金公司之间资源配置策略相似性的欧氏距离的临界值。然后将各公司持有的每只股票持股数量与公司持股总量的比率作为向量（未持有即为0），采用相同的方法进行分析，最后综合公司每只股票占持股总市值比率以及持股总量比率的结果，得到两家公司资源配置相似的欧式距离的取值范围。

5.2 研究方法

利用聚类分析度量两个对象之间的相似性，通常有两种方法，一种是对所有对象作特征投影，另一种则是距离计算。在此，通过聚类分析中的距离计算，衡量对象之间的差异度来反映对象之间的相似度关系，从而度量两两公司之间的相似性。

为了使新增加的公司不会影响到任意两个公司之间的距离，因此，在聚类分析[5]中，构建了对象之间的欧氏距离：

5.3 占比持股总市值分析

在占比持股总市值分析中，通过计算两两公司之间的欧式距离，构建了表4的相似矩阵，进而定量描述不同基金公司之间资产配置策略的相似性。

表4 10家基金公司个体间欧式距离的相似矩阵（占比持股总市值）

为了更直观的描述各公司之间相似程度，通过聚类分析，画出如下谱系图，如图2所示。根据谱系图，可将10家公司分成5类，1～5类分别为{F}, {B,D,E,H,I,J}, {G}, {C}, {A}，其中，D(D,B)=8.474, D(E,B)=5.588, D(H,B)=6.765, D(I,B)=8.306, D(J,B)=7.078, D(E,D)=6.796, D(H,D)=8.867, D(I,D)=7.474, D(J,D)=6.046, D(H,E)=6.918, D(I,E)=6.841, D(J,E)=4.797, D(I,H)=6.225, D(J,H)=7.191, D(J,I)=6.137，这6家公司被化为一类，说明这6家公司具有一定的相似性，其中两两公司之间的欧式距离最大值为8.867，最小值为4.797，可知，当欧式距离小于最小值时，两家公司距离更近，因此，衡量两家公司相似性的临界值为8.867。

图2 10家公司聚类分析的谱系图（占比持股总市值）

5.4 占比持股总数分析

在占比持股总数分析中，通过计算两两公司之间的欧式距离，构建了表5的相似矩阵，进而定量描述不同基金公司之间资产配置策略的相似性。

表5 10家基金公司个体间欧式距离的相似矩阵（占比持股总数）

按照上述方法绘制的谱系图如图3所示，根据谱系图，同样将10家公司分为5类，1～5类分别为{I}，{B,D,E,H,J},{C}, {F}, {A,G}，其中，D(D,B)=10.175, D(E,B)=8.530, D(H,B)=9.604, D(J,B)=9.863, D(E,D)=8.414, D(H,D)=10.830, D(J,D)=8.679, D(H,E)=10.110, D(J,E)=5.431, D(J,H)=9.953, D(G,A)=8.585，E, J, D, B, H这5家公司被分为一类，其欧式距离最大值为10.830，A和G被分为一类，其欧式距离为8.585<10.830，因此，按照单只股占总持股数的比例分析，其度量相似性的临界值为10.830。

图3 10家公司聚类分析的谱系图（占比持股总数）

5.5 结果分析

根据上述模型求解的过程，按照不同的数据处理方法进行聚类分析，求解各对象间的欧式距离，得到不同的临界值如表6所示。

由表6可知，按照占比持股总市值的相似性临界值为8.867，占比持股总数的相似性临界值为10.830，由于考虑到相似性度量的精确程度，选择较小的临界值能更好的的衡量对象间的相似性，因此，当两基金公司间的欧式距离≤8.867时，可断定，两公司的资源配置策略相似。

表6 相似性临界值比较

6 结论及建议

根据上述分析，公司在进行投资时应尽可能地将效用以及风险进行平衡，通过上述模型，计算出投资效用-VaR最优值，以免造成为了达到效用最大化而忽视风险或为了达到风险最低化而忽视效用的情况。另外，利用上述模型，研究不同基金公司间的相似性，可以为公司在资产配置组合上提供相关建议，通过与自身相似公司的财务状况、运营状况、以及管理等方面反省自身，快速转变，及时止损。这些对公司的基金资产配置降低了风险，具有重大意义。

[1] 王瑶，赵治荣. 上证月平均收盘价走势的统计分析——基于ARMA模型[J]. 太原师范学院学报：自然科学版，2019, 18(04): 40-42, 64.

[2] 董晓羿，申世昌. 基于ARMA-EGARCH模型对我国人寿保险的实证分析[J]. 齐齐哈尔大学学报：自然科学版，2019, 35(04): 74-77.

[3] 张贺清. 均值和方差变动的马科维茨投资组合模型研究[D]. 哈尔滨工业大学，2015.

[4] 徐惠，闫云侠，朱家明. 基于AHP的基金资产配置策略分析[J]. 哈尔滨师范大学自然科学学报，2020, 36(04): 80-87.

[5] 章永来，周耀鉴. 聚类算法综述[J]. 计算机应用，2019, 39(07): 1869-1882.

Analysis of fund asset allocation strategy based on systematic risk

SUN Chen-yang1，WANG Xue-qi1，WANG Xue2

(1.School of Statistics and Applied Mathematics, Anhui University of Finance and Economics, Anhui Bengbu 233030, China; 2.School of Economics, Anhui University of Finance and Economics, Anhui Bengbu 233030, China)

In order to analyze the fund asset allocation strategy from the perspective of systemic risk, this article uses the ARMA model to predict stock prices, and constructs a linear programming model to establish the optimal stock investment portfolio strategy. Secondly, comprehensively consider the income and risks of each company's asset allocation, construct the Markowitz portfolio model and the investment utility-VaR balance model, and give the corresponding investment utility and risk value under the optimal portfolio strategy. Finally, a similarity measurement model based on cluster analysis is established to analyze the similarity of asset allocation among companies.

ARMA；Markowitz；VaR；cluster analysis；similarity

2021-03-15

国家自然科学基金（71974001）；安徽省教研项目（2018jyxm1305）；安徽财经大学教研项目（acjyyb2020011）

孙晨阳（1999-），女，河南郑州人，本科，主要从事数学与应用数学研究，1249830016@qq.com。

F832.52;F224

A

1007-984X(2021)05-0081-06