汽车电动尾门系统力学分析与研究*

蔡言龙 薛斌 刘利宝

（1.烟台霍富汽车锁有限公司；2.长城汽车股份有限公司）

随着汽车工业技术的发展与进步，汽车的舒适性和智能性成为各个主机厂的重点研究方向。传统的汽车尾门系统需要人工操作，不能实现自动闭合，费时费力，越来越不受客户青睐；而新型电动尾门系统操作简单、智能化程度高，不仅可以实现自动闭合，而且配合传感器可以实现“防夹”、“防撞”、“脚踢操控”等功能，备受客户追捧。目前，相关学者和研究人员对电动尾门系统的控制方案和原理、电动撑杆的受力和安装点等内容进行了分析和研究[1-4]，但是对整个尾门系统的力学分析和研究较少。文章针对某SUV车型电动尾门系统，建立整个系统的力学模型，并基于MATLAB进行仿真计算，在尾门系统运动过程中，对电动撑杆进行了力学分析。这一分析对整个电动尾门系统的结构布置、驱动方案优化具有重要意义，对后续车型尾门系统的设计和研发提供有效参考。

1 电动尾门系统结构组成

汽车电动尾门系统主要由控制单元（ECU）、电动撑杆（驱动单元）、闭锁器、锁扣、传感器和电子线束等构成。图1所示为某SUV车型电动尾门系统执行结构示意图。

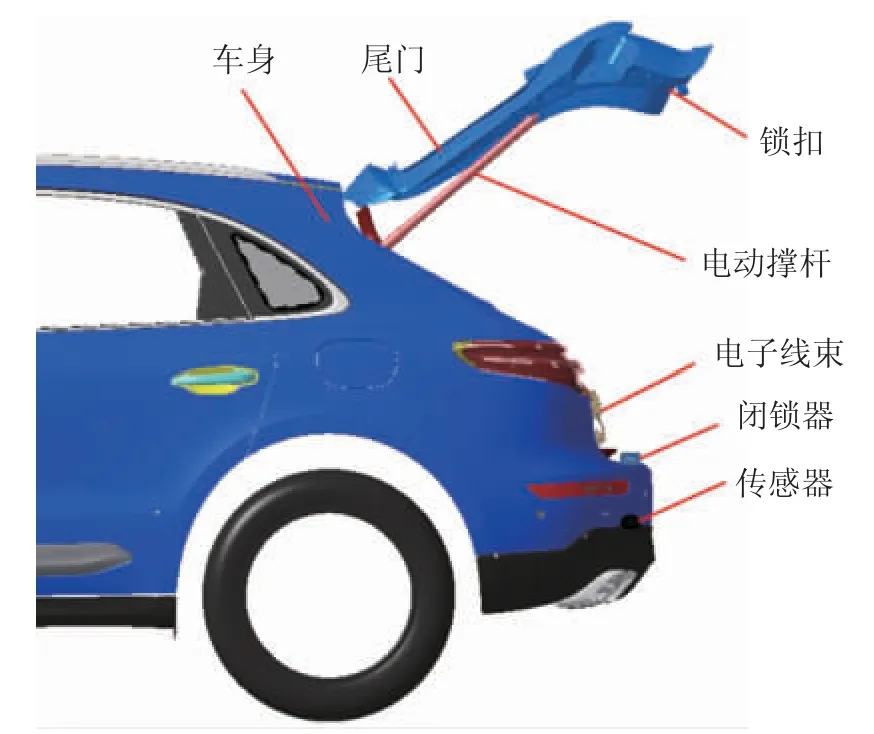
图1 电动尾门系统执行结构示意图

电动撑杆（驱动单元）是整个尾门系统的关键核心部件，其作用是连接车身和尾门，是整个电动尾门系统的驱动机构和执行机构。图2所示为电动撑杆结构示意图，主要由两端球头、弹簧、弹簧套管、丝杆、丝杆螺母、丝杆套管、轴承、适配器、减振器、制动器、驱动器、连接块、减速器（行星齿轮）、电机、外套管和线束等组成。当撑杆接到ECU指令时，电机会通过减速器、连接块等结构带动丝杆螺母运动，将电机的旋转运动转化为丝杆螺母的直线运动，控制撑杆的伸缩，在弹簧的共同作用下，实现汽车尾门的开启与闭合。

图2 电动撑杆结构示意图

2 系统力学模型建立

以SUV汽车电动尾门系统为例进行简化分析，建立单撑杆汽车尾门系统力学模型，如图3所示。在模型建立时对系统相关条件和参数做以下假设：

图3 单撑杆汽车尾门系统力学模型图

1）假设尾门铰链处和撑杆球头两端没有摩擦；

2）忽略电动撑杆自身重力因素；

3）假设汽车尾门系统沿整车坐标系XZ面左右对称；

4）假设尾门系统在开启、闭合过程中，尾门和撑杆平稳运行，无振动，无其他干扰因素。

基于上述假设，以尾门和车身铰链点为原点（O点），按整车坐标系方向建立模型坐标：X方向与水平面平行，指向尾门后方；Z方向与水平面垂直，指向上方。将电动撑杆沿模型坐标系XZ面进行投影，F's为电动撑杆在力学模型中的输出分力。A点为撑杆球头与尾门铰接点，B点为撑杆球头与车身铰接点，W点为汽车尾门半侧重心点。G为汽车尾门半侧重心所产生的重力，θ为点A和坐标原点O连线与X轴夹角，α为点A和坐标原点O连线与点W和坐标原点O连线夹角。Mg为重力G对铰链点O产生的转矩；Ms为撑杆输出分力F's对铰链点O产生的转矩。

考虑车辆停车时还有上坡、下坡等工况，定义车辆停驶路面的坡度角参数，在力学模型中将其等效转化为重力方向G与竖直平面的夹角β。另外，根据实车电动撑杆空间安装条件，电动撑杆会以铰接点B为中心，向XZ平面内倾斜，定义为撑杆内倾角γ，如图4所示，Z方向与水平面垂直，指向上方；Y方向与X和Z方向垂直，指向驾驶员侧；Fs为电动撑杆的输出力。

图4 电动撑杆安装内倾角视图

根据力矩平衡原理可知,尾门和车身铰链点O的合力矩为0，即：

尾门重力G对原点O产生的扭矩：

式中：Lg——重力G对原点O产生的力臂。

式中：Lw——尾门重力点W到原点O的距离。

撑杆输出分力F's对原点O产生的扭矩Ms：

式中：Ls——撑杆与尾门铰接点A对原点O产生的力臂。

式中：LA——撑杆与尾门铰接点A到原点O的距离；

Bx，Bz——撑杆与车身铰接点B在模型下的坐标值。

由力学分析可知，电动撑杆输出分力F's：

式中：γ——电动撑杆安装内倾角。

公式（1）～（6）组成的数学方程组即为单撑杆汽车尾门系统数学模型，由此可以推导出电动撑杆输出力Fs的表达式，如下：

当尾门绕铰链点O转动时，即角θ发生变化时，便可求出电动撑杆的输出力Fs的值。由公式（7）可知，影响撑杆输出力的参数有尾门重力、尾门质心点、撑杆车身安装点、撑杆安装内倾角、停驶路面坡度角等；且撑杆输出力与尾门重力、尾门质心与铰链点的距离、撑杆安装内倾角成正比，与撑杆车身安装点与铰链点的距离成反比；在安装条件固定的情况下，电动撑杆的输出力Fs是单一变量角θ的函数。

3 基于MATLAB仿真计算

为了方便研究电动尾门系统在开启和闭合过程中，电动撑杆的输出力曲线，运用MATLAB仿真软件，建立单撑杆汽车尾门系统数学模型，然后根据某SUV车型实车状态，设定尾门系统特性参数，如表1所示。

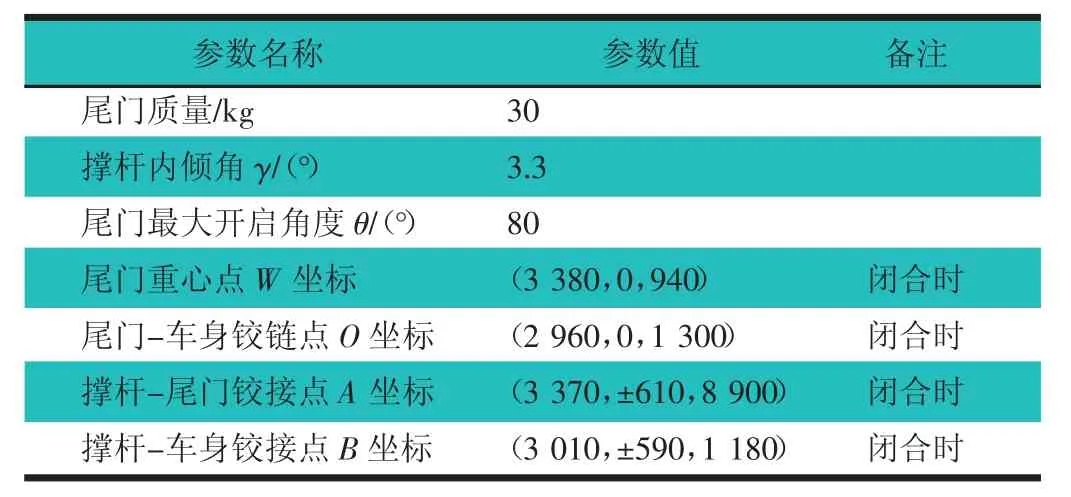
表1 某SUV车型电动尾门系统特性参数

基于MATLAB仿真模型和设定参数，分别求解车辆在平坡（0°）、上坡（20°）、下坡（-20°）3种停车工况下，撑杆输出力Fs与尾门转角θ在开启和闭合过程中的曲线关系，如图5所示。

图5 3个工况撑杆输出力曲线图

通过对撑杆输出力与尾门转角的曲线关系图，可以得出如下结果：1）尾门在开启和闭合过程中，上坡、下坡和平坡3种工况，撑杆输出力与尾门转角均呈非线性关系，且开启和闭合曲线变化趋势都很相近。2）尾门开启过程：上坡和下坡工况的撑杆的最大输出力，要大于平坡工况。其中，上坡工况，转角为0°时撑杆输出力最大，值为50 N；下坡工况，转角为80°时撑杆输出力最大，值为43 N；平坡工况，转角为70°时撑杆输出力最大，值为35 N。3）尾门关闭过程：上坡、下坡和平坡3种工况的撑杆最大输出力基本相近。其中，上坡工况，转角为80°时撑杆输出力最大，值为41 N；下坡工况，转角为30°时撑杆输出力最大，值为43 N；平坡工况，转角为40°时撑杆输出力最大，值为42 N。

4 结论

通过建立电动尾门系统力学模型和基于MATLAB仿真计算，可以分析得出以下结论：1）电动撑杆输出力与尾门重力、尾门重心与铰链点的距离、撑杆安装内倾角等参数成正比，与撑杆车身安装点与铰链点的距离成反比；2）在撑杆安装条件固定的情况下，撑杆的输出力是尾门转角θ的单一变量函数，且上坡、下坡和平坡3种工况下，均呈非线性关系；3）尾门开启过程，撑杆输出力在上坡和下坡工况下要大于平坡工况，尾门关闭过程，撑杆输出力基本相近。基于本课题的研究现状，进一步可以展开对雪载荷、风载荷等工况的理论分析和研究，并增加试验分析和验证。