多流束水表设计中的CFD应用
2021-07-01郑玉斌
郑玉斌
(杭州水表有限公司,浙江 杭州 310000)
1 引言
多流束水表是旋翼式和螺翼式水表中的一种结构形式,因其多个进水口的特点,叶轮受力均匀,且机芯不易被堵塞,从而成为目前国内最主流的机械式计量的水表。然而,此类水表机械结构复杂,牵一发而动全身,任意结构的改变都可使得水表的流量性能千差万别。如何从全局研判水表流量性能趋势,并经济、快速地找到解决问题的方法是全行业的迫切需求。
计算流体动力学(Computational Fluid Dynamics,CFD)因兼有理论性和实践性的特点,是一种可以非常有效地提供解决此类复杂流动的技术和方法。
2 水表的功能和理论依据
水表是一种在测量条件下,用于连续测量、记录和显示流经测量传感器的水体积的一种仪表。其测量对象是水,测量参数是体积。
由其定义和功能可知,水表测量的水必须满足连续式方程(质量守恒定律)。如图1所示 ,封闭管道中的任意两个截面积,流经第一个截面积的流体(水)全部流过第二个截面积,即有

不考虑测量管段前后的温差,忽略密度变化的影响,即。这是水表用于计量的理论 依据。
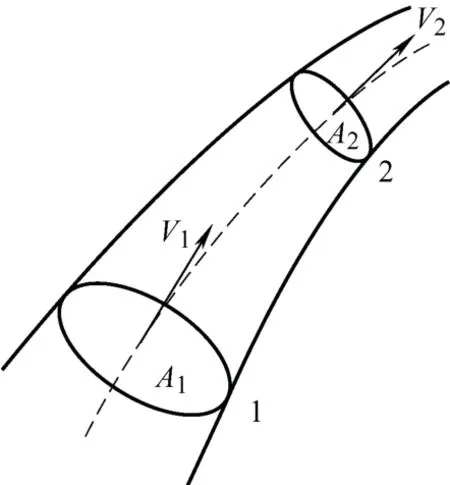
图1 封闭管道中的不同截面
流量Q
=截面积A
×流速V
。由于表型结构确定,截面积A
不变,故流量Q
仅是流速V
的函数,即水表测量参数可以由测量水体积改变为测量流速,这是一类水表设计的理论依据。以流速为测量参数的水表统称为速度式水表,具体到多流速水表,测量参数为叶轮的转速。3 理想流体的力学理论
我们知道,对于多流束水表结构,带压力的水流沿叶轮盒内圆周切向流入,如图2所示,形成点汇和点涡叠加的流动。根据势流的叠加原理,强度为q
的点汇和旋转环量为Γ
的点涡叠加后的势函数和流函数分别为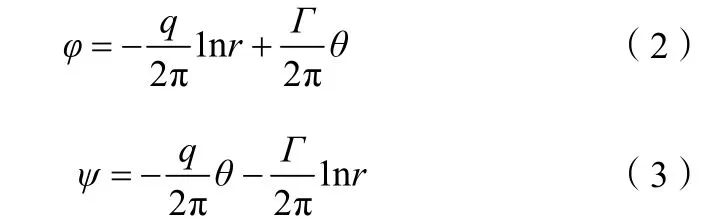
由于等流函数线就是流线,则有

即得到流线方程为的螺旋线。

图2 叶轮盒内形成的叠加流动
当水流冲击叶轮的叶片时,会对叶轮产生作用力,并产生转矩,使叶轮绕旋转中心(叶轮盒顶尖)转动,并带动水流进行螺旋流动。旋流是多流束水表典型的流体运动形式流体的运动,可以用一组非线性的偏微分方程组来描述。根据柯西-亥姆霍兹定理,若以下行列式不等于0,如式(6)所示,则表明该流场中的流动为有旋流动。根据质量守恒定律(连续性方程)可知,流入叶轮盒内的是有势的质量流(压力水流),∇V
≠0,即叶轮盒内流场的全部区域中连续地充满着绕自身轴旋转的水流体微团。于是,形成了一个角速度为ω(x
,y
,z
,t
)的涡线集合。涡线是t
时刻,各流体微团沿曲线转动的轴线,流体微团的角速度ω方向和其在曲线上位置的切线方向一致,其微分方程为
根据螺旋线方程和旋流特性设计了螺翼式叶轮,即螺翼式叶轮叶面是水表在某一流速下螺旋线在转角(时速)上的积分,如图3所示。螺翼式(尤其是转动轴与水流方向平行的水平螺翼式)叶轮因为具有大通量的特性,在大口径水表中应用广泛。
4 优化设计中的仿真与分析
通过改变某些变量和初始条件,可方便地得到不同设计、不同工况下工作状态。以多流束旋翼式叶轮盒设计为例:设计1中叶轮盒设计有6个进口栅和6个出口栅;设计2中叶轮盒进口栅不变,出口栅更改为4个,并确保进出口的总截面积不变。给定进口压力和出口流量,介质水为牛顿流体,通过CFD仿真计算,可获得如下结果。
4.1 最小流量Q1时设计1(左侧)和设计2(右侧)进出口栅处的速度云图
如图4所示,Q
时设计1的进口流速(左上)小于设计2的进口流速(右上),设计1的出口流速(左下)大于设计2的出口流速(右下),表明设计2的水表始动性能更好,水表更灵敏;设计1的进口流速梯度和出口流速梯度大于设计2的进出口流速梯度,表示设计2速度平均,叶轮转动平稳,有较少的静压力和水动能损失。设计1的流速差异大,更容易导致叶轮转动不平衡和齿轮喘动,加速叶轮顶尖的磨损。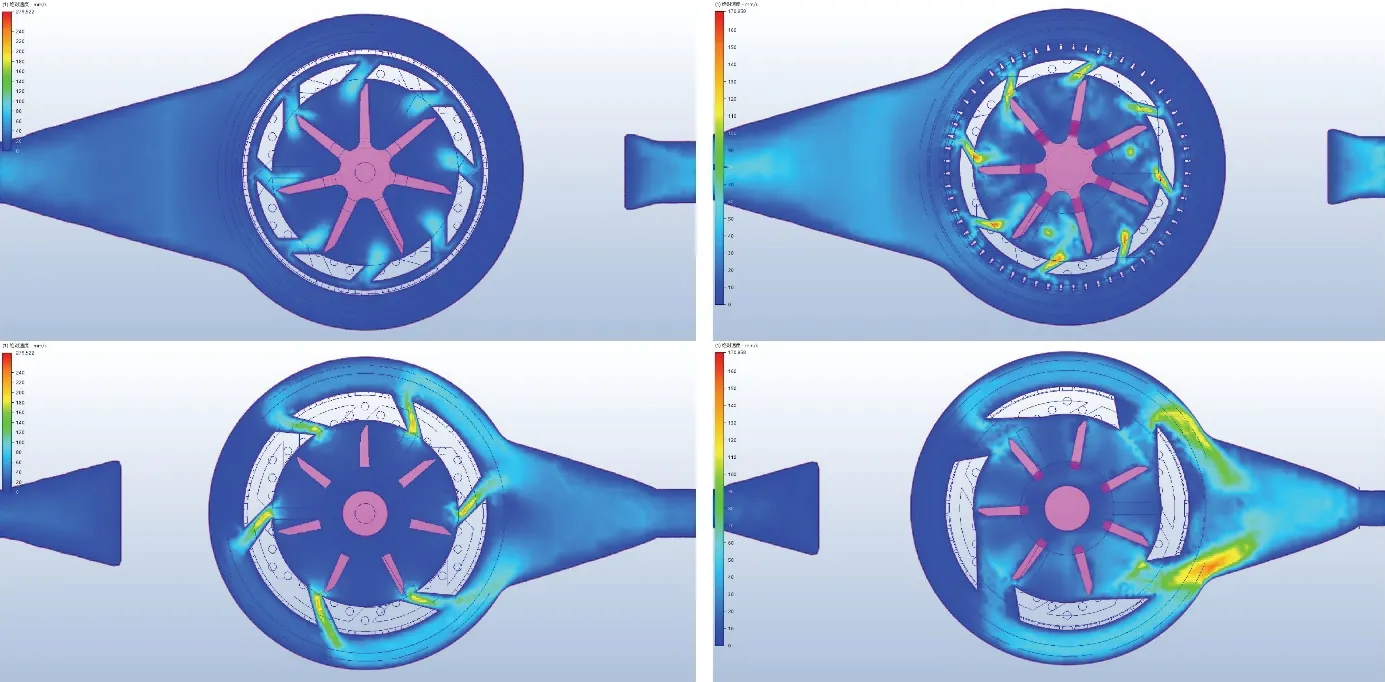
图4 Q1时,不同数量的出口栅对进口和出口流速的影响
4.2 常用流量Q3时设计1(左侧)和设计2(右侧)的进出口速度云图
如图5所示,Q
时设计1的进口流速(左上)小于设计2的进口流速(右上),设计1的出口流速(左下)大于设计2的出口流速(右下),符合实际经验值。设计1的进出口流速差异大,表明设计1有更多的压力能被损耗,导致水表压力损失大。另外,设计1的速度分布不均衡,也容易引起叶轮和传动齿轮运转不平稳,导致水表走慢,并大大降低了转动轴的实用寿命。
图5 Q3时,不同数量的出口栅对进口和出口流速的影响
4.3 出口压力比较
压力损失Δp
也即水表压降,是水表所造成的不可恢复的压力降低,即压力损失Δp
=表前进口压力均值−表后出口压力均值,它是水表性能的重要参数之一。不同流量,水表的压力损失不同,一来情况下,流量越大,其压力损失越大。额定工作条件下,在压力损失最大(即Q
)时,设计1和设计2的对比结果明显。本例已给定进口压力0.4 MPa,故获取出口压力的平均值即可计算出压力损失。
计算设计1的出口压力平均值为0.350 MPa;设计2的出口压力平均值为0.37 MPa,故而设计1和设计2的压力损失Δp
分别为0.05 MPa和0.022 MPa。参照相关标准定义,设计1和设计2的压损等级分别为Δp
63和Δp
25。如图6所示,设计1的出口压力波动频繁,表示其出口栅对出口压力影响大;而设计2的出口压力波动大,表明其出口压力更容易受到叶轮转动的影响。设计1水通量小,流动阻力增加,因而其压力损失较大,更多的流体动能转化为反向压力能,导致在相同工况下必须提高供水压力,故而不利于节能环保。
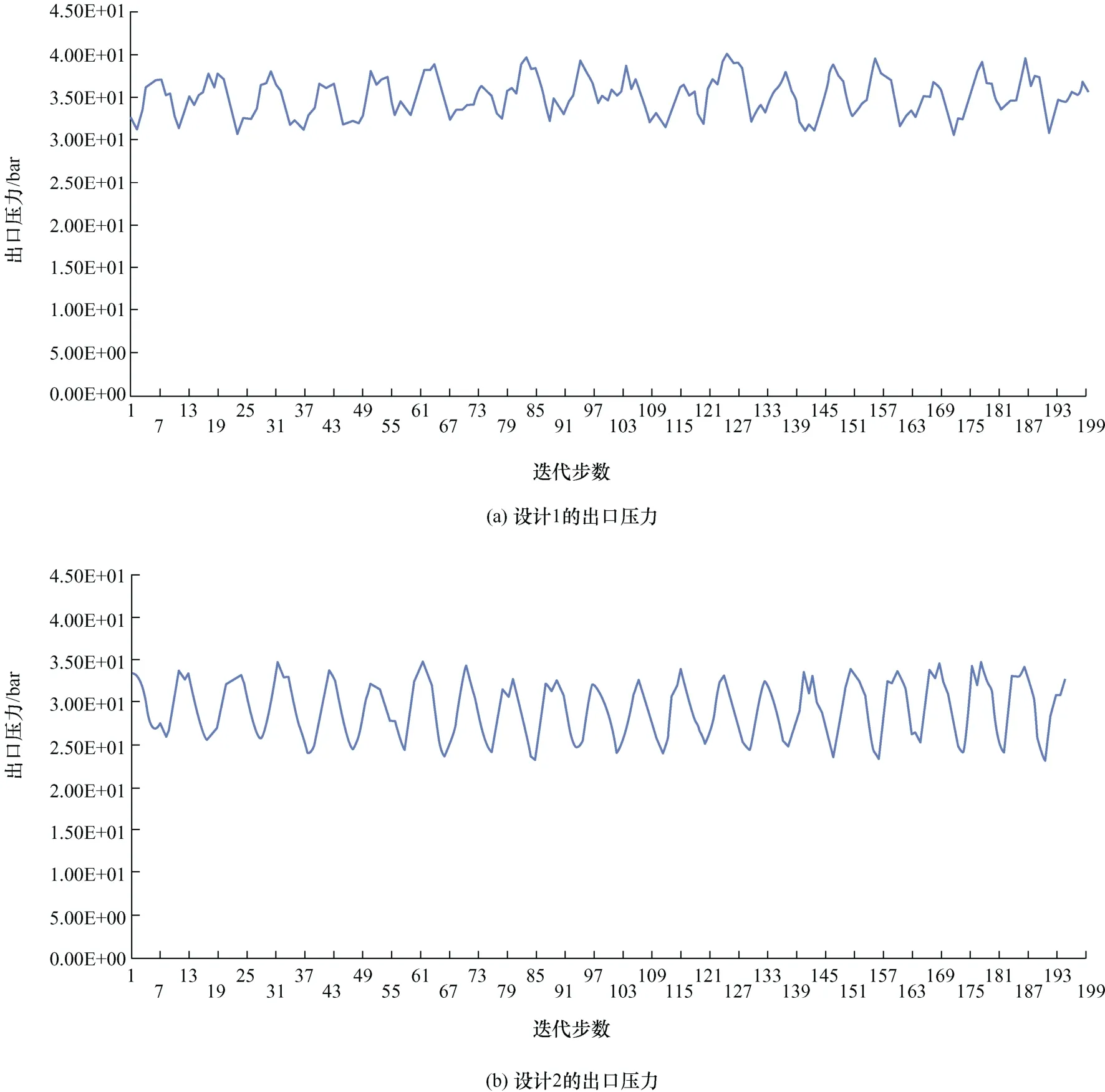
图6 出口压力
4.4 叶轮转速比较
由速度式水表设计的理论依据可知,测量流经水的体积即测量叶轮的转速,故叶轮的转速是衡量水表性能的关键指标。
利用CFD仿真得到的叶轮转速和设计转速对比,可以计算水表性能好坏的重要参数——示值误差,以相对误差的百分比表示其定义公式如下由水表设计理论依据,上式即为


Q
≤Q
≤Q
)的最大允许误差MPE为±2%;低区流量(Q
≤Q
<Q
)的最大允许误差MPE为±5%。典型的水表示值误差曲线如图7所示。
图7 典型的水表示值误差曲线
以公称流量Q
为4 m/h,量程比80的水表为例,计 算数据表格如下。表 量程比80的水表计算数据
?
其绘制的示值误差曲线如图8所示。
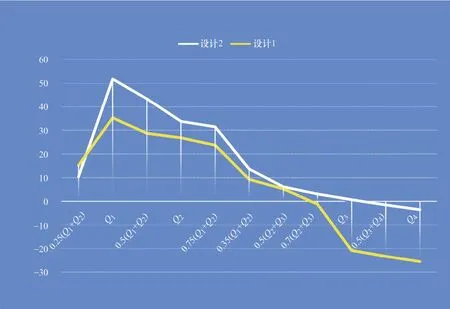
图8 示值误差曲线图
图8表明,CFD计算绘制的示值误差曲线趋势接近典型的水表示值误差曲线。但因为排除了表壳和叶轮等触水零件的表面粗糙度而形成的内摩擦效应,消除了阻力对低区流量的影响,从而使得水表在低区流量运行时走快。从设计1和设计2的示值误差曲线对比来看,出口栅的改变对高区流量时叶轮转动影响较大,即单个出口栅截面积越小,水表走得越慢。这和叶轮上部(齿轮盒底部)的三条阻尼筋对高叶轮转速的影响异曲同工。
常用流量Q
为4 m/h时,设计1和设计2的叶轮转速对比如图9所示。计算可得设计1和设计2的叶轮转速均值分别为1 188.75 r/min和1 509.88 r/min。根据叶轮转速对比图可知,设计1叶轮转速波动范围大,转动平稳性较差,脉动流和旋涡时空分布不均,从而影响水表的检验和调校。同时,也加快如叶轮顶尖等转动零部件的磨损,降低水表的使用寿命,增加用水计量成本。设计2叶轮转速变化规律,其产生的脉动流和旋涡具有可预测性。经验表明,脉动流和旋涡具有促使水表走快的作用,使得水表示值误差偏向正值,对水表始动差的水表有益。设计2的叶轮平均转速高,符合压损小,叶轮和水的动能高的经验值。
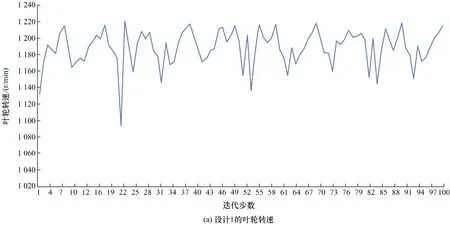
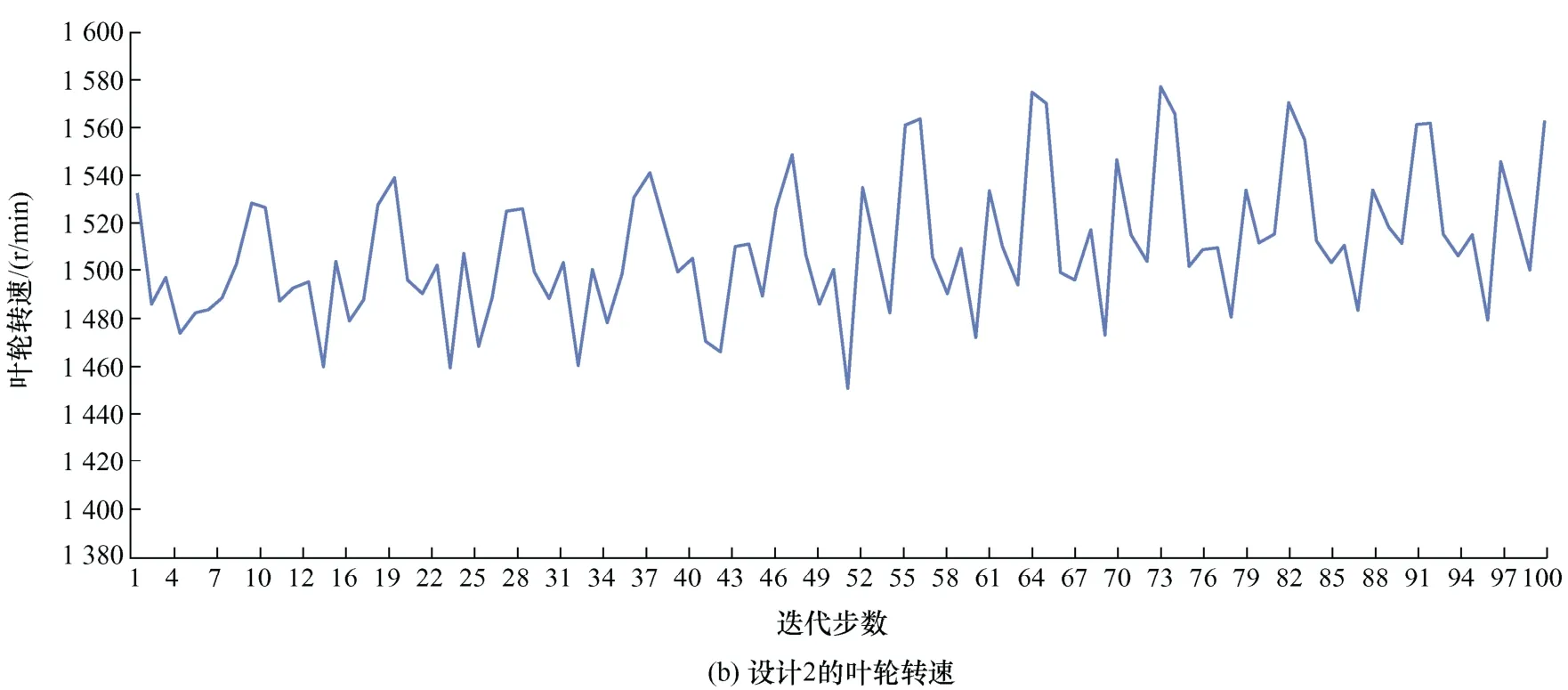
图9 设计1和设计2的叶轮转速对比
综合图4和图5,叶轮盒出口栅由6个变为4个的设计对水表始动有很大的改善,水表灵敏度越高,水表的量程就越宽,应用范围就越大,计量越精确。速度梯度越小,叶轮转速越平稳;压力损失小,更有利于管网用水调节,节约资源。
通过CFD监控进出口压力,可以直接得出特定流量下压力损失Δp
的数值,从而为设计优化提供决策依据。4.5 叶轮盒优化前后的实例图片
如图10所示为优化前叶轮盒的实物结构,即设计1;如图11所示为优化后叶轮盒的实物结构,即设计2。

图10 优化前叶轮盒的实物结构

图11 优化后叶轮盒的实物结构
5 结束语
受限于数值模型、求解方法和网格划分等各个因素,尤其是实际每只水表与数值模型个性化的差异,CFD计算结果可能与实际情况差异较大,故而不能直接作为设计的评判依据,但其为水表设计的改进提供趋势和方向是可行的。
基于理想流体的流态分析是为了简化多流束水表复杂工况而提供的一种仿真计算方式,便于在水表设计阶段引入CFD仿真计算,模拟多工况下的工作状态,输出可视化结果,从而可以大大减少实验和设计迭代次数,缩短开发周期,节约成本,提高市场竞争力。同时,从对水表流量性能单一影响因素入手分析,可以积累经验数值;举一反三,为全因素、多工况的模拟仿真打下坚实的基础。
