考虑磨损的接触式端面密封模型及试验

惠玉祥, 刘 莹, 王悦昶, 黄伟峰, 李永健

(清华大学 摩擦学国家重点实验室，北京 100084)

端面密封在旋转机械中起着重要的作用，化工流程中95%左右的旋转设备采用了端面密封[1].接触式端面密封普遍工作在混合润滑状态，密封件端面磨损不可避免，进而导致泄漏率增加引发密封失效，密封失效可能造成严重的人身安全事故和重大财产损失[2].因此，考虑摩擦磨损的接触式端面密封性能理论与试验研究，对工程实际应用具有重要的指导意义.

自1885年端面密封出现以来，学者们建立多种模型对接触式端面密封性能进行评估和分析.Lebeck[3]首次用统计学方法建立了混合润滑模型，证明了表面特征对接触式端面密封性能有关键性意义，Wen等[4]建立了混合摩擦热流固耦合模型，进一步量化了表面粗糙度等对接触式端面密封性能的影响.王小燕等[5]使用有限差分和有限单元法，建立了三维多场耦合模型，对核主泵用接触式端面密封性能进行了分析.Zhou等[6]利用ANSYS软件建立了端面密封的有限元模型，讨论了压力、转速等端面密封变形及温度的影响.

密封端面磨损也是研究的热点之一，目前广泛应用的仍为Archard[7]于1953年通过研究机械磨损时，提出的基于黏着磨损的磨损定量模型[8–10].顾永泉等[11]基于Archard磨损理论，通过引入磨损系数给出了接触式机械密封的磨损率定量公式，魏龙等[12]也基于Archard黏着磨损理论，从分形角度揭示了磨损率和端面分形参数的关系，用以预测软质密封面的磨损情况.Yeon-Wook Kim等[13]建立了数学模型以有效预测一定范围内石墨作为密封材料的磨损率，并通过试验进行了验证.于如飞等[14]以Archard黏着磨损模型以及Winkler弹性基础模型，从磨损深度出发预测铰链副的寿命，并通过计算实例进行了验证.

上述端面密封的代表性研究工作可分为两类，其一是关注密封性能分析的混合润滑模型；其二是关注密封端面磨损的定量研究，两类研究之间缺乏联系.但在实际问题中，磨损与接触式密封性能之间存在强耦合关系，对密封性能分析和寿命预测乃至优化设计均有重要意义.针对该问题，本文作者基于流体承载和固体接触承载共同平衡闭合力的传统思路，引入Archard定量磨损模型，创新性地提出沿窄端面径向方向磨损均匀假设，从而使用半解析方法得到近似固体接触力、流体承载力及介质膜厚分布.在此基础上耦合密封环组件力和热变形，最终得到密封泄漏量、端面温度等性能参数.通过台架试验验证了本文中提出的考虑稳定磨损的半解析模型的可行性.

1 理论模型

图1为一种典型的油润滑接触式端面密封(冲洗结构未画出).密封内外压差使得一部分密封介质进入密封端面处，介质润滑和固体接触并存，接触式端面密封工作在混合润滑状态.此时，密封开启力由流体压力及固体粗糙峰接触力组成.密封组件的主要失效形式是端面磨损导致的闭合力下降引发的泄漏量增加.根据经典磨损理论，磨损过程一般经过3个阶段：跑合阶段、稳定磨损阶段、失效阶段.密封组件的全寿命周期中大量时间处于稳定磨损阶段，磨损率相对稳定.对稳定磨损阶段开展分析具有现实意义和工程应用价值.此外，大量接触式端面密封工作在油润滑状态.综合考虑模型的工程问题导向性，本文作者基于油润滑接触式端面密封稳定磨损阶段建立相应模型.

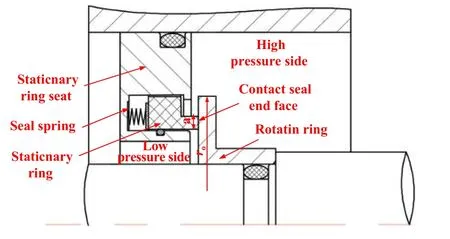
Fig.1 A typical single mechanical seal图1 典型接触式端面密封示意图

本节中首先基于密封件材料的标准摩擦磨损试验结果，探讨了Archard磨损模型的适用性.随后基于Archard磨损模型的定性分析结果提出模型基本假设.从基本假设出发，结合密封组件开启力和闭合力平衡的基本原理，获得密封界面固体接触力、流体承载力、流体膜厚度的近似半解析公式.在此基础上，通过有限元方法计入密封组件热、力变形，得到与传统密封分析模型中“热流固耦合”相对应的简化模型.

1.1 分析Archard磨损模型的适用性

依据接触式端面密封工况范围，在标准摩擦磨损试验机Plint TE-92上，采用600 N压力，油温保持80 ℃，进行了密封副摩擦磨损标准试验，磨损前后的石墨表面形貌如图2所示.

磨损前可以发现在石墨基体上，存在着很多孔隙[图2(a)黄色标注所示]，黑色部分为碳石墨基体，白色部分为石墨材料的浸渍物.试验前浸渍物只能部分填充石墨孔隙.试验后形貌则表明，石墨环表面孔隙基本被磨损脱落后的石墨及浸渍物颗粒填平.这一现象表明密封件材料在摩擦过程中发生了黏着磨损，能够应用Archard磨损模型进行刻画.

1.2 基本假设

Archard磨损模型是基于金属材料的黏着磨损机理建立的磨损定量模型.本文研究对象是金属/石墨在油润滑条件下的混合润滑摩擦磨损.通过1.1的分析表明，其磨损形式可以近似为黏着磨损.因此后续分析做出如下假设：

(1) Archard磨损模型公式如下所示[10]：

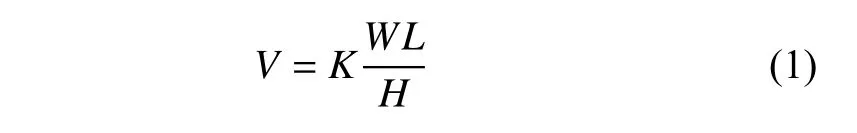
Fig.2 SEM micrographs of seal face before and after wear图2 密封副石墨材料端面磨损前后形貌的SEM照片

式中：V为体积磨损率，单位为m3/s；K为磨损系数，虽然影响因素比较复杂[10]，但在指定工况下一般为常数；W为承载压力，单位为 P a，因为只有固体接触力会导致磨损发生，所以这里W特指密封端面处某一点的固体接触力；L指这一点的摩擦行程，其大小在密封环匀速转动时与线速度v成正比，单位为 m；H为较软材料的表面硬度，一般由材料本身性质决定.即在公式适用的条件下，磨损只和线速度及接触压力有关；

(2) 接触式端面密封多为窄端面设计以减小发热，假设密封环面满足端面宽度a远远小于密封环半径r0，即

(3) 假设磨损过程表面材料去除为各向同性，即不产生犁沟；

(4) 假设密封环为轴对称结构，以建立简化二维(2D)模型；

(5) 1.1小节的试验结果表明，硬质材料密封环无显著磨损，因此假设磨损主要发生在软质材料密封环上.

1.3 处理混合润滑的半解析模型

对于接触式端面密封，正常工作状态下，应该满足端面开启力与闭合力平衡，即：

式中Fopen、Fclose分别为端面密封开启力、闭合力，其中闭合力主要由内外压差和弹簧弹力提供，可以通过端面密封几何结构以及具体工况得到[1].而开启力由流体承载力和固体接触力构成.

式中：Fl、Fc分别为总流体承载力和总固体接触力，单位都为N，对于流体承载力，根据假设(1)和假设(2)，且密封端面为名义平面，近似认为密封界面只存在流体静压效应，即流体压力沿着半径方向线性分布，进而，根据内外压差可以求出近似流体承载力.

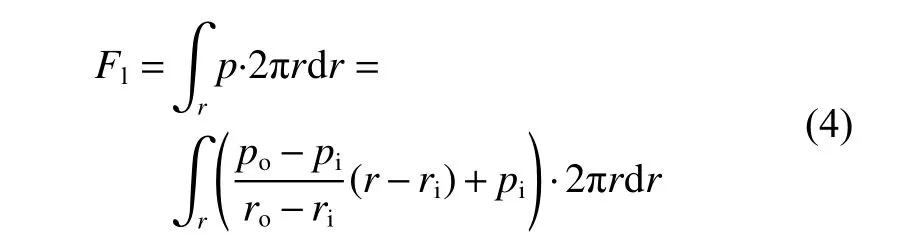
式中：pi,po分为为密封内外流体压力，单位为Pa，ri,ro分 别为密封端面内外径，单位为 m，r为密封面半径，单位为 m ，p为 液体承载压力沿着半径r分布.将式(4)带入式(3)，则总固体接触力Fc为

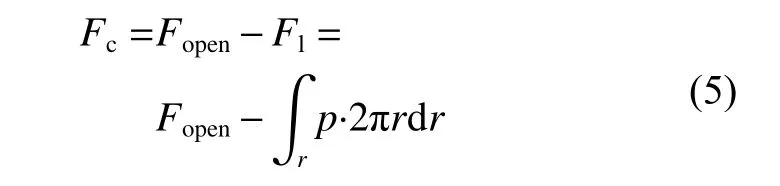
通过力平衡关系[见式(2)]及Archard磨损模型[见式(1)]可对接触式密封在磨合阶段的端面磨损情况进行定性分析.由于轴对称结构假设(4)，仅考虑沿半径方向的磨损.不妨设磨合阶段在密封端面半径r处磨损最为严重，这一现象的原因可能为安装误差、密封组件变形等.而该位置由于磨损严重，材料损失较快，固体接触力下降，根据Archard磨损模型可知该位置的磨损率会减小；而另一方面，该位置接触力的下降改变了开启力和闭合力的平衡状态，由于窄端面假设(2)，密封界面流体承载力总体有限，力平衡关系主要依靠固体接触力实现，因此半径上必有另一位置的固体接触力自适应增加以恢复力平衡关系，从而再次影响磨损率.从准稳态角度考虑这一调节过程，即窄端面接触式端面密封的端面磨合阶段的最终效果为在稳定磨损阶段，端面沿半径方向磨损率一致，即为均匀磨损.这一结论是本文理论模型的基础.

根据Archard磨损公式(1)，因K，H为常数，若保持沿半径方向磨损率相同，则在转速一定情况下，沿半径方向的接触力应和各半径处对应线速度成反比：

即可以认为接触力沿径向分布满足关系式：

式中：b为 待求解常数项.将式(7)带入式(5)即可得到b：

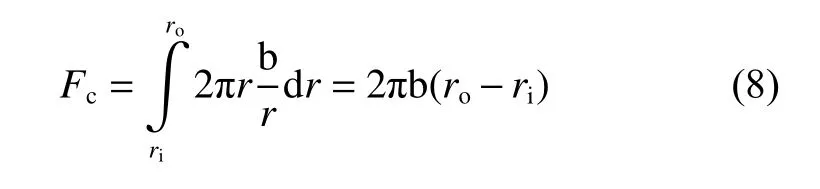
得到固体接触力径向分布后，可通过接触力学粗糙表面接触力计算方法反解沿径向的等效流体膜厚度分布.首先，考虑经典粗糙表面接触力计算的弹塑性接触模型[15].该模型将两个粗糙表面等效为1个粗糙表面和1个绝对光滑平面，并将粗糙面上的粗糙峰近似为球冠，球冠半径大小为等效粗糙度大小(见图3).

在粗糙表面相互靠近时，首先是少量粗糙峰接触，带来较大的接触压力，导致粗糙峰塑性变形.而随着密封端面的进一步靠近，粗糙峰接触数目变多，部分粗糙峰发生弹性接触，与塑性接触产生的力共同构成了固体接触力.塑性变形和弹性变形分别使用Chang[15]提出的塑性接触模型和经典粗糙峰弹性接触模型GW模型[16]来进行计算，其在2D模型中表现如下：

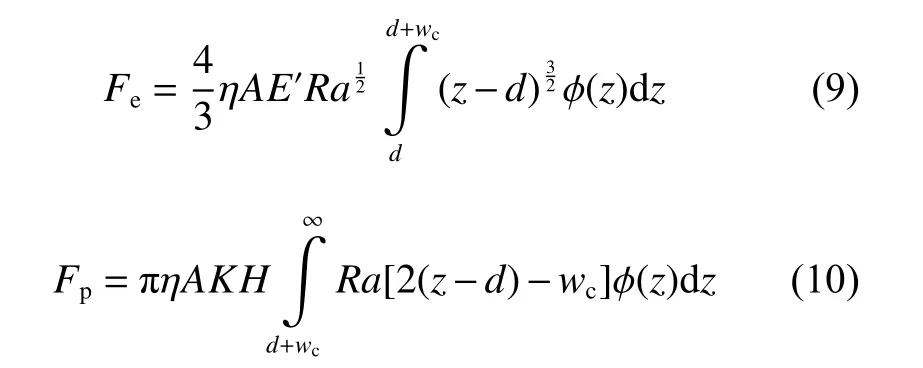
式中：A为接触面面积，ϕ (z)、E′、η分别为等效面的高度概率分布、等效弹性模量、表面形貌参数，wc为弹性变形和塑性变形的临界点，Fe为弹性力，Fp为塑性力.基于各向同性的磨损过程假设(3)，表面形貌的高度概率分布保持不变，即 ϕ (z)保 持不变，d和h为 变量，即Fe和Fp由 膜厚h直接决定，且为非线性变化.当已知表面形貌参数和密封环材料参数，可以直接由膜厚根据公式(9)和公式(10)求解出该膜厚下的对应接触力Fc.而由公式(8)已经得到固体接触力沿半径方向的分布，可以通过拟合直接反解出膜厚.

1.4 密封组件热力耦合

接触式端面密封组件的性能分析中，组件本身的热、力变形对系统性能的影响是不可忽略的[2].通过1.3小节已经实质上处理了接触式端面密封界面的混合润滑问题，获得了界面流体润滑膜厚度、流体承载力及固体承载力分布.为建立面向工程实际的接触式端面密封的模型，本节中进一步通过有限元方法引入密封组件的力热效应，建立等效于密封研究中常见的“热流固耦合模型”的简化模型.

全域旅游是以旅游目的地为整体区域进行建设规划、形成整体区域规划、培育整体产业、创造整体场景、进行资源全面分享的发展模式。为了促进绿色、创新、协调、开放和共享的发展旅游,促进旅游业的升级转型,国家旅游局宣布建立“国家全域旅游示范区”,促进中国旅游业的转型由“景点型”到“全域旅游”。

首先考虑热效应耦合.密封系统中一般有3个热源：端面摩擦生热、搅拌热和外部传入热.其中，搅拌热仅在某些极端情况下为主要热源[2].一般情况下，密封系统主要热源为端面摩擦热.因此，本文中只考虑密封端面摩擦热进行分析建模.接触式端面密封的摩擦热主要由两方面组成，即粗糙峰接触摩擦热及密封介质剪切热.

考虑润滑油为牛顿流体，剪切热可以由下列式子得到：

剪切力：

生热功率：

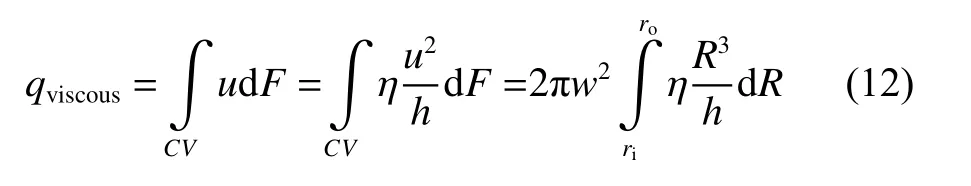
而固体接触力的摩擦热则可通过下式计算：

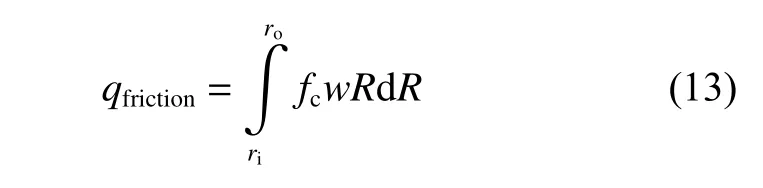
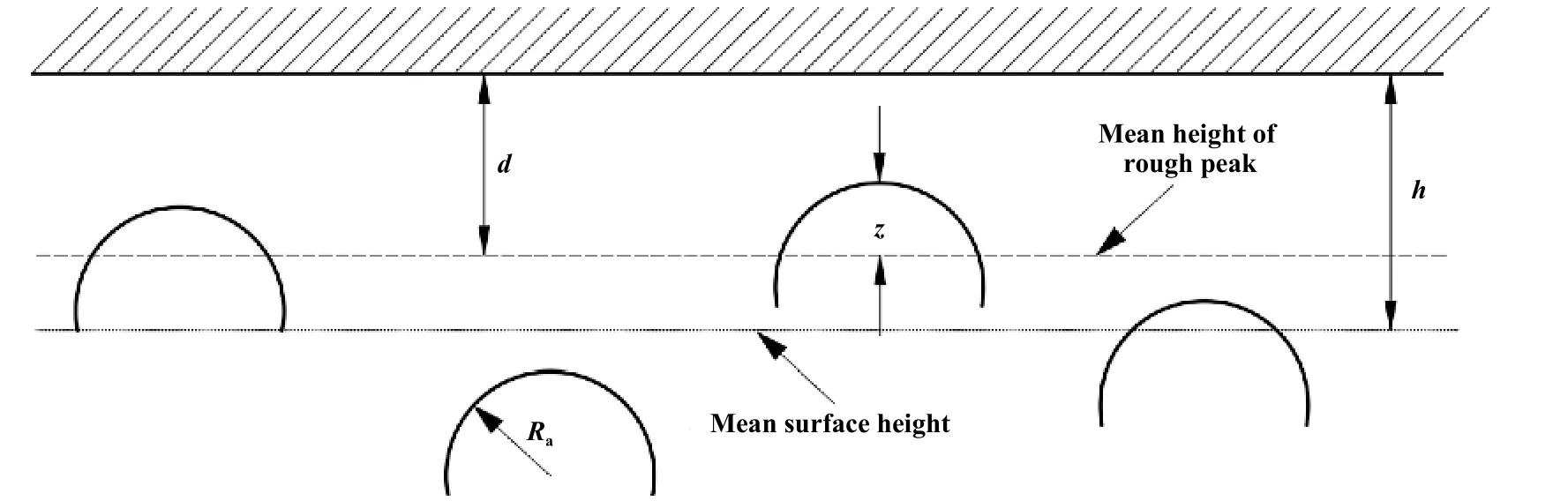
Fig.3 Schematic diagram of solid contact force calculation图3 固体接触力计算示意图

式中fc可以由Amonton’s摩擦定律求得：

µ为固体摩擦系数，本文中选用0.1.最终端面生热的总功率为

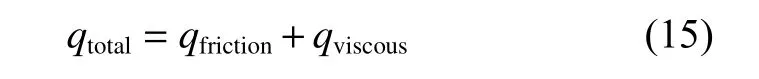
除热效应外，端面流体承载力和固体接触力和密封组件浸没状态的内外压差均会导致组件变形，此即为力效应.基于1.3和本节的结果，可以采用有限元方法对密封组件进行建模，对热力效应进行求解.本文中所建立有限元模型动环为不锈钢材料，静环为石墨，边界条件设置如图4所示.

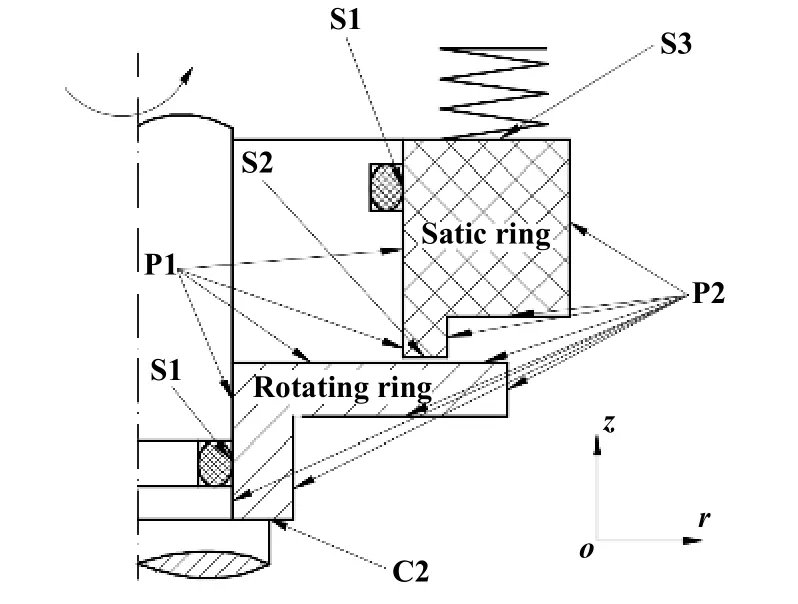
Fig.4 Schematic diagram of boundary conditions图4 边界条件示意图

总体来看，边界条件分为力边界条件、热边界条件以及位移边界条件.根据密封结构及使用工况条件，上述边界条件分别阐述如下：

力边界中P1为低压侧外部压力(大气压)，可以反映外部压力对系统变形的影响，P2为高压侧腔体内部压力(绝对压力0.4 MPa)，可以反映腔体内部流体对密封系统变形的影响，S1处为O型圈支反力，是内外压差的分界点，可以通过Karaszkiewicz[17]提出的方法进行估算.S3为弹簧力施加边界.S2为密封端面流体和固体接触力分布施加点.

热边界条件中，对于暴露在外或者有冲洗的面，设置为对流换热边界，对流换热系数由式(16)计算.式中Do为 静环外径直径，单位为m，Pr为流体的普朗特常数，v为流体的运动黏度，单位为： m2/s， ω 为动环角速度，单位为 r ad/s，λ为流体的导热系数.根据本文研究对象的实际工况与几何参数计算得到对流换热系数为937 W/(m2gK)，其余为绝热边界.S2处施加端面生热，其主要来源分为流体剪切热以及固体摩擦生热[18].在施加S2处热源时，由于动环和静环采用不同材料，导热性能不同，且结构不同，所以热量不会在动环和静环均匀分配，因此根据热平衡进行动态分配.

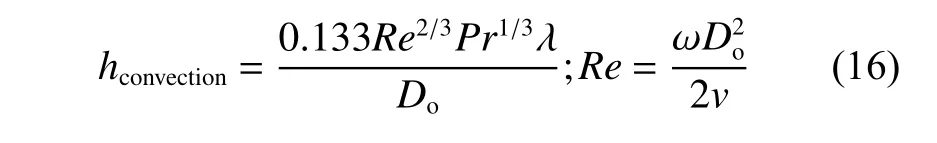
此外由于密封端面间隙极小，可认为z方向流体温度不变.而根据Reynolds提出的黏温效应公式，温度场的计算结果会对黏度产生影响，应进行修正：

式 中：η为温度为T时的黏度，单位为 Pa·s， η0为T0= 313K时的黏度，为 2.755×10−2Pa·s，β为常数，取−2.814×10−2.对修正后的黏度由式(12)重新求解流体剪切生热，重新求解温度场分布，直至收敛，温度场求解完成.

位移边界中动环实际结构中由轴向台阶定位，可视为变形基准点，对C2施加动环z方向位移约束.由于静环为补偿环，静环位移约束一般施加在质心处.

最终，采用上述有限元热力耦合分析可获得动静环的变形.对于稳定磨损，由于假设磨损全部发生在软材料静环，因此，考虑热力效应后的静环磨损后形状应定性符合动环在工作状态下的端面变形后形状.

1.5 密封性能评估

密封性能评估主要包括计算密封泄漏量、温度分布、端面形状等.其中温度分布和端面形状可以由上面的过程直接求得，而泄漏量Q，可以通过公式(18)求得：

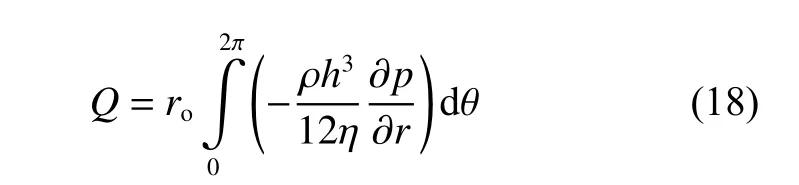
式中：ro为 密封端面外径，单位为m，ρ、η分别为密封介质的密度和动力黏度，单位分别为 g/m3和 Pa·s.具体计算流程见图5.

2 试验验证

为验证理论模型，设计了油润滑接触式端面密封试验系统，对不锈钢-石墨配副端面密封特性进行试验研究，测量了温度、泄漏量和稳定磨损状态过后端面形貌等，通过重复试验验证结果的可信性.

2.1 试验参数及内容

表1列出了试验用密封无量纲几何参数，物理参数以及工况条件.

表1 试验部分参数Table 1 Main parameters of experiment

密封端面温度使用热电偶和温度巡检仪进行测量；由于接触式端面密封泄漏量非常小，因此采用相机拍摄泄漏油滴数进行估计；磨损后表面通过白光干涉仪对表面进行观测.试验系统实物如图6所示，主要用到的有高速电机、油气润滑系统、油循环冷却系统、温度检测仪、摄像机和恒温油箱等.

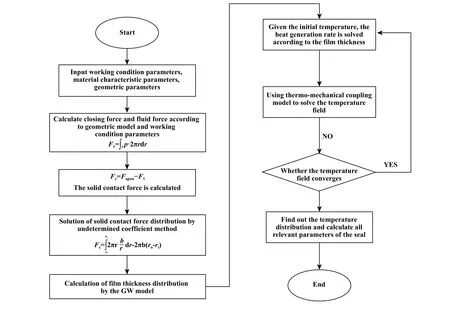
Fig.5 Calculation flow chart of uniform wear model图5 均匀磨损模型计算流程图

2.2 试验历程

试验分为预试验和正式试验两部分.预试验旨在验证腔体压力为0.4 MPa时静止状态试验腔体密封性以及各环节密封性.

正式试验时，首先开启油泵循环，调节腔体压力至0.4 MPa，开始计时和记录速度以及泄漏量，按照0.125 m/s2的 加速度升速至48.7 m/s，稳定转速运行，直至支撑滚动轴承温度升高至90 ℃或时间到达15 min，停机冷却，这是防止轴承温度过高，发生危险.重复试验直至总时长达到1 h，最后拆下静环对磨损端面进行观测，并进行重复试验，绘制成图7的流程图.

2.3 试验结果分析

按照本文中建立的理论模型，有限元部分采用COMSOL5.3实现，其余计算采用MATLAB2012b计算，最终得到给定试验条件下的密封性能以及磨损情况，并与试验实际结果进行对比.

2.3.1 温度

将两次试验所测得温度数据和理论计算结果绘制成图8，其中Exp-1-1，Exp-1-2，Exp-1-3，Exp-1-4为第一次试验，Exp-2-1，Exp-2-2，Exp-2-3，Exp-2-4为重复试验结果，Theoretical calculation为理论计算在磨损均匀的情况下的端面温度.

Fig.6 Overall layout of the experiment图6 试验整体布置图

同等工况下，使用理论模型密封界面温度计算结果为236 ℃，而试验结果都在190～215 ℃范围以内，其一部分误差来源于热电偶距离实际密封端面有微小距离，如图9所示，温度会比实际温度稍低.因此理论模型温度和试验温度基本吻合.

2.3.2 泄漏量

试验测得的泄漏量和理论计算的泄漏量进行对比，如图10所示，其中Experiment 1为第一次试验，Experiment 2为重复试验：

从泄漏量结果来看：4次测得的泄漏量结果均都低于理论预测值.主要原因分析如下：在计算泄漏量时，使用的都是高温黏度下的泄漏量，而由于试验室条件有限，泄漏量的测量采用数滴数的形式，其温度已经下降，因此计算所用的液体黏度小于实际试验液体黏度，导致计算的泄漏量偏大.另一方面泄漏量误差来源于泄漏油滴内包含溶于油滴的石墨，密度增大，导致总体液体表面张力变大，每滴油滴实际所含油比理想情况要多，而采用数滴数来计算泄漏量时，试验值将会偏小.

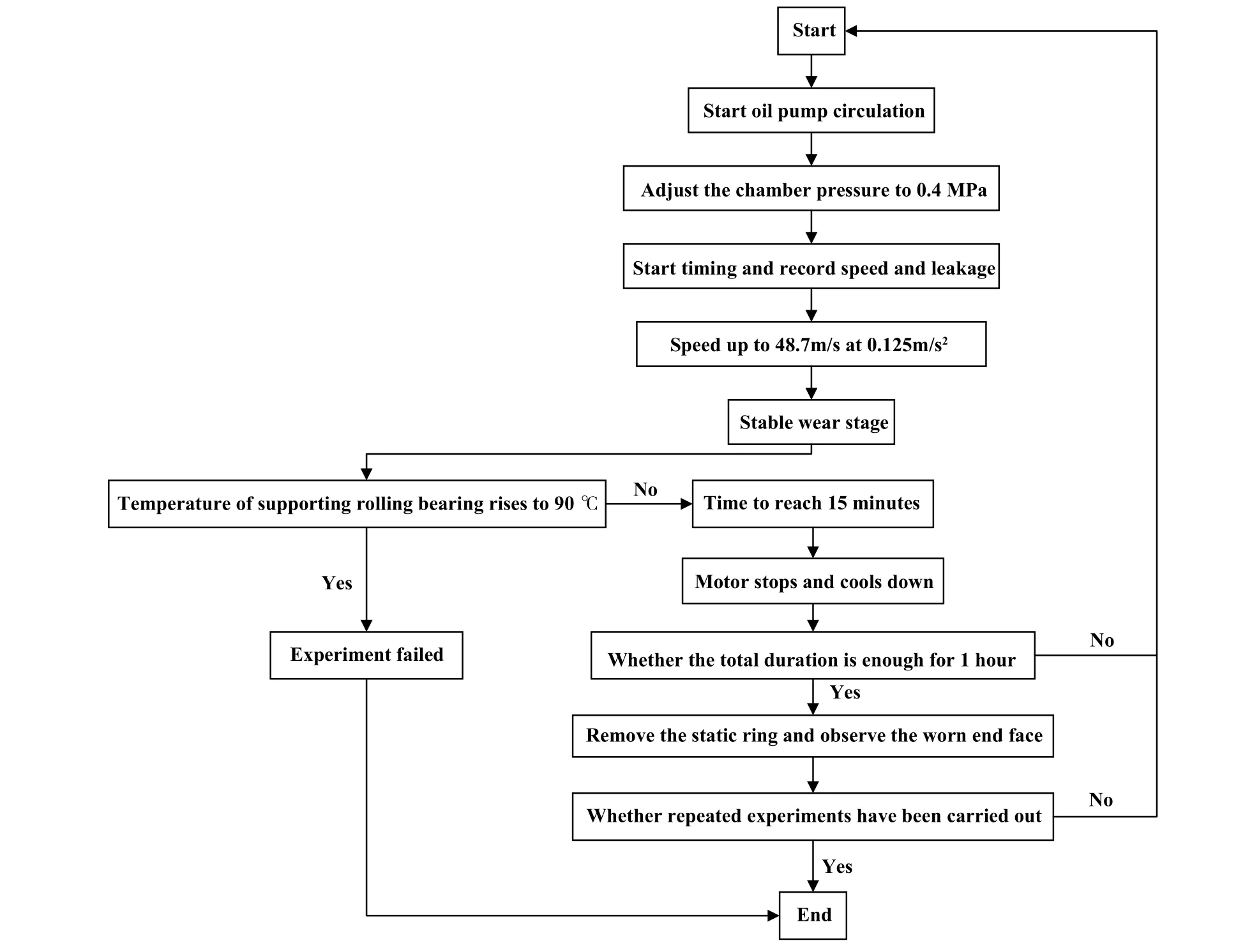
Fig.7 Experiment flow chart图7 试验流程图

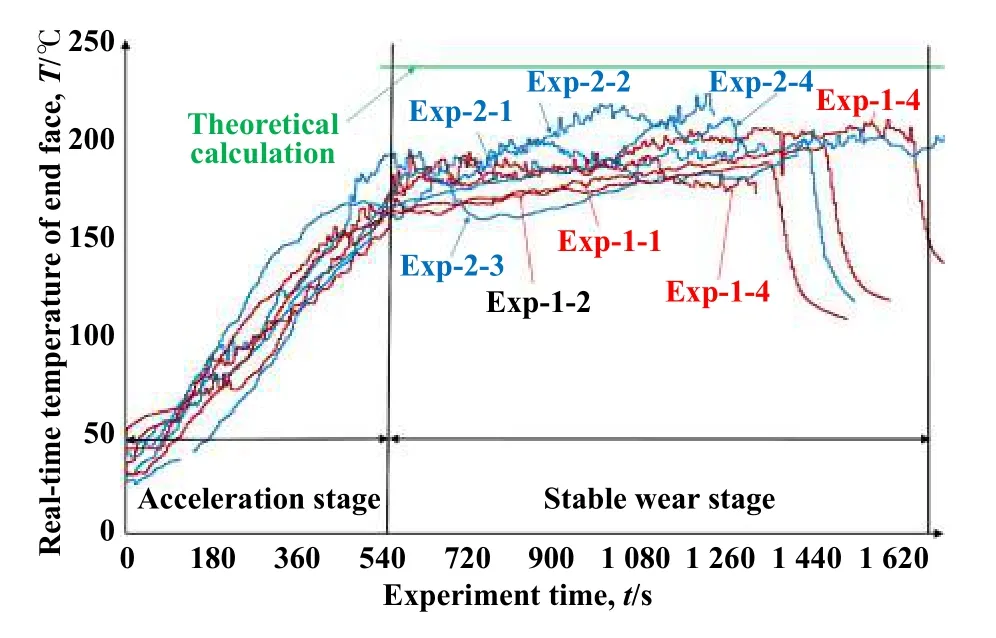
Fig.8 Comparison on experimental temperature and theoretical model temperature图8 试验温度与理论模型温度对比图

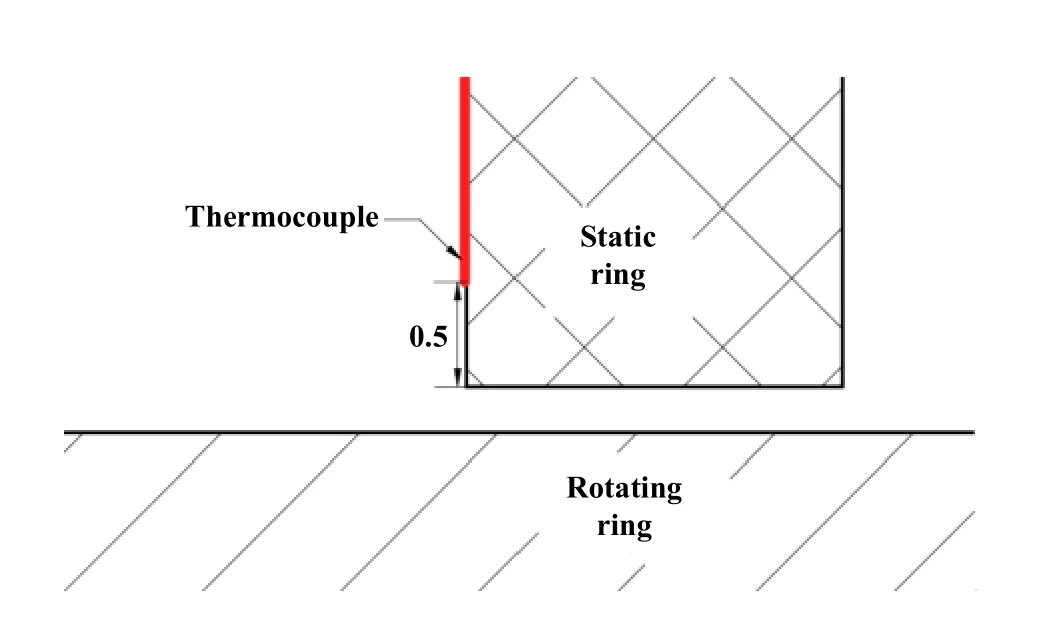
Fig.9 Thermocouple installation diagram图9 热电偶安装示意图

2.3.3 密封环端面磨损

对试验磨损后的静环即软环进行三维端面形状观测，得到其沿径向表面磨损情况，如图11(b)红色曲线所示.

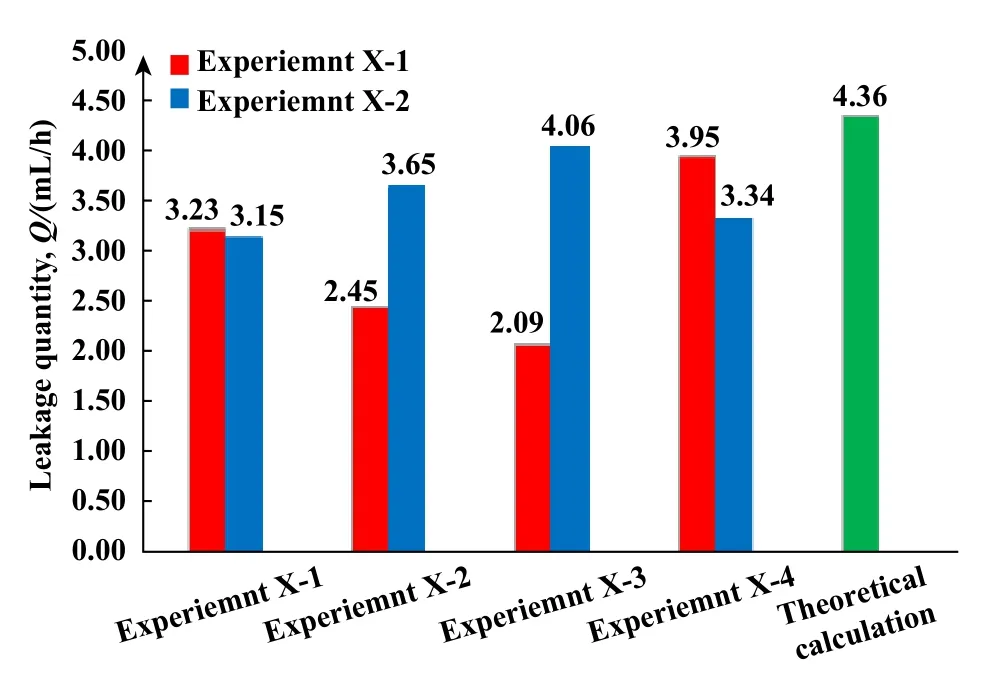
Fig.10 Comparison on experimental leakage and theory图10 试验泄漏量与理论对比图

由理论模型可知，静环实际磨损情况应为动环变形形状和膜厚之和.膜厚变化如图11(a)所示，其变化为0.003 5 μm，而变形导致的磨损理论值为0.38 μm，膜厚变化相对于变形磨损不足1%，因此忽略不计，静环实际磨损后应该和动环变形大致吻合.从图11(b)中可以看出，动环模拟变形最高点和最低点差为0.38 μm，而静环磨损最高点和最低点之差为1.4 μm，但静环内径处发生的较为严重的磨损差为0.71 μm，这可能是由于内径处发生了石墨在高温下磨损后浸渍物的析出和结块而形成局部磨粒磨损造成的，磨损后可以观测到内圆周靠近端面有较为严重的结块现象，如图12所示.

但整体磨损趋势基本相同，因此该理论模型较为准确地预测了稳定磨损阶段的磨损情况，这也验证了假设(5)的合理性.

3 结论

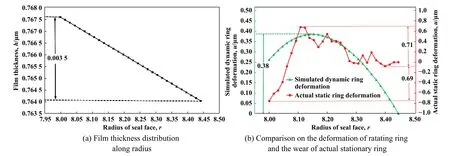
Fig.11 Wear analysis of seal face图11 端面密封磨损分析

Fig.12 Schematic diagram of caking at internal diameter图12 内径处结块示意图

a.Archard磨损模型适用的条件下，沿窄端面径向方向端面磨损在稳态磨损阶段近似均匀，磨损率为常值.在此基础上耦合密封环组件力、热变形，最终得到密封泄漏量、端面温度等性能参数.通过台架试验验证了本文中所提出的考虑稳定磨损的半解析模型的可行性.

b.基于径向磨损均匀假设，可得到替代混合润滑模型的半解析方法求解密封界面近似固体接触力、流体承载力及介质膜厚分布.

c.耦合半解析模型和热力效应有限元模型，提出稳定运行状态油润滑接触式端面密封性能与磨损的快速分析模型并得到试验验证，对密封性能分析和寿命预测乃至优化设计均有重要意义.