基于偏心风荷载分布模型的柔性支撑索分配系数研究
2021-06-30马文勇柴晓兵赵怀宇马成成
马文勇, 柴晓兵, 赵怀宇, 马成成
(1.石家庄铁道大学 土木工程学院,石家庄 050043; 2.河北省风工程和风能利用工程技术创新中心,石家庄 050043)
太阳能是分布式能源重要组成部分,光伏发电是开发利用太阳能资源最有效形式之一。为了适应污水处理厂、渔塘等区域光伏产业的发展,柔性光伏支架广泛应用。柔性支架是由柔性索(钢丝绳或钢绞线)、钢立柱、钢梁和斜拉索或钢斜柱组成的支撑体系,光伏组件由连接件固定在柔性索上,其跨度大、柔性大、质量轻等特点决定了风荷载是其主要荷载。目前,国内外对光伏风荷载研究主要集中在传统固定光伏支架上,对柔性光伏支架风荷载的研究涉及较少,小倾角柔性支撑光伏组件表面风荷载分布规律和风荷载分布模型仍不完善,另外,柔性光伏支架支撑索风荷载分配对支架抗风设计具有重要影响。
我国《光伏发电站设计规范》(GB 50797—2012)[1]和《光伏支架结构设计规程》(NB/T 10115—2018)[2]风荷载体型系数取值均采用均匀分布模型,也就是垂直于光伏组件风荷载体型系数值沿底部到顶部保持一致,且对于倾角小于15°光伏组件,体型系数均按15°取值。日本《太阳能光伏发电系统的设计与施工》[3]风压系数也采用均匀分布模型取值,并给出了风压系数和倾角的关系。这两种取值方式无法反映风荷载在光伏组件表面的不均匀分布[4]。欧洲规范[5]参考开敞单坡顶盖风荷载采用九区域分布模型,进行工程设计时,取值比较麻烦。另外,我国《建筑结构荷载规范》(GB 50009—2012)[6]给出的单坡屋盖风荷载体型系数值迎风端和背风端不同,这与美国土木工程学会(ASCE)[7]规定的开口屋盖风荷载体型系数类似,在进行光伏支架结构设计时也可参考。
目前国内外对光伏支架风荷载研究主要集中在组件表面风荷载分布规律,对风荷载分布模型研究相对缺乏。李寿科等[8-9]通过刚性模型测压风洞试验获得单坡光伏车棚和双坡光伏车棚表面风荷载分布规律,并给出风荷载取值建议。Kopp等[9-11]通过风洞试验对屋面光伏表面风荷载分布规律进行研究。龚敏等[12]通过刚性模型风洞试验发现作用在光伏组件上的风荷载具有渐变性,且从光伏组件底部到顶部大致呈均匀过度。Sorensen[13]认为作用于光伏方阵上的风压呈三角形分布。贺广零等[14]基于光伏组件表面风荷载分布不均的特点提出风压大致呈梯形分布。马文勇等[15]通过刚性模型测压风洞试验研究传统固定支撑光伏组件表面风压分布和支架整体风荷载,提出考虑弯矩影响的四角点平面分布风荷载模型和偏心风荷载分布模型,并研究了阻塞度对组件风压分布的影响。
不同于传统固定支撑光伏组件,柔性支撑光伏组件倾角一般较小,且仅由两个柔性索支撑,其表面风压分布以及上、下支撑索风荷载分配系数仍不明确。本文通过刚性模型测压风洞试验获得柔性支撑光伏组件表面风荷载分布规律,提出柔性支撑光伏组件偏心风荷载分布模型,考虑整体力和弯矩之间的关系,并基于该模型计算上、下支撑索风荷载分配系数,为柔性太阳能光伏支架抗风设计提供依据。
1 风洞试验介绍
此试验为刚性模型测压风洞试验。试验在石家庄铁道大学风洞实验室[16]低速试验段进行,低速试验段尺寸为4.4 m宽、3 m高、24 m长。低速试验段最大风速为30 m/s,背景湍流度I≤0.4%。
1.1 试验模型
图1为风洞试验模型及参数定义。按照1∶4进行缩尺,缩尺后单块光伏组件的尺寸为248 mm长、410 mm宽、12 mm厚。光伏组件由ABS板制成,单块组件共布置60个测点,上下表面各30个,位置一一对应。最大阻塞度(倾角20°)为1.32%。

图1 试验模型及参数定义
1.2 试验概况
试验采用均匀流场,来流风速为9 m/s。压力扫描阀采样频率为330 Hz,采样时间为30 s。5块光伏组件并联称之为单排,图1(a)中1~5表示5个位置,中间位置指的是位置3。间距比S/L为0.08。风向角α为0°~180°,15°间隔。倾角β为0°~20°,5°间隔。
1.3 参数定义
定义单块光伏组件风压系数:
(1)
(2)
定义单排光伏组件风压系数:
(3)
式中:Cpi(t)为i测点风压系数;Pui(t)和Pdi(t)为i测点上表面和下表面风压;Cp为光伏组件风压系数,即体型系数;Ai为i测点代表的面积。
定义弯矩系数:
(4)
(5)
式中:CMx和CMy分别为绕x轴和绕y轴的弯矩系数;xi和yi分别为i测点的坐标。
2 光伏组件风荷载分布规律
目前《光伏发电站设计规范》和《光伏支架结构设计规程》对光伏组件风荷载体型系数均采用均匀分布模型取值,未考虑弯矩的影响。本节基于柔性支撑光伏组件表面风荷载分布规律,提出考虑整体力和弯矩关系的偏心距风荷载分布模型。
2.1 组件风荷载随风向角变化规律
满足支架和组件安全必须考虑风向角对组件风荷载的影响,图2给出了单排光伏组件风荷载体型系数随风向角的变化曲线,体型系数为正表示光伏组件上表面受风压力作用,体型系数为负表示光伏组件上表面受风吸力作用。可以发现,风压力极大值通常发生在0°和30°风向角附近,风吸力极大值通常发生在150°和180°风向角附近。风荷载极大值可能发生在不同风向角的规律与江继波等[17]应同时考虑0°、30°、45°、135°、150°和180°风向角下组件的风荷载规律一致。因此,迎风面积大小并不是决定光伏组件风荷载大小的唯一因素。不同倾角光伏组件风荷载随风向角变化规律类似,以倾角10°单排光伏组件为例,图3给出了不同位置光伏组件风荷载体型系数随风向角的变化曲线,可以看出,风荷载最大值对应的风向角与整体分析类似,因此,在进行柔性太阳能光伏支架设计时,建议综合考虑150°和180°两个风向角,作为结构设计的最不利荷载。
不同倾角光伏组件风荷载随安装位置变化规律类似,以倾角10°为例,图4给出了光伏组件风荷载体型系数随安装位置的变化曲线,可以发现,中间区域(位置2、3、4)光伏组件风荷载较大。气流流经单排光伏组件时,中间区域光伏组件两侧绕流受限,加速顶部和底部绕流,加速绕流使更多气流由尾流夹卷进入剪切层,使剪切层的曲率半径减小,降低背风面压力,从而导致中间区域光伏组件风荷载大于两侧组件,文献[15]也提到光伏组件中央区域所受风荷载强于边缘。图5给出了不同倾角中间位置(位置3)光伏组件体型系数随风向角的变化曲线,可以看出,风荷载极大值风向角与图2和图3分析一致,因此,下文主要围绕这四个不利风向角展开分析。

图2 单排光伏组件体型系数随风向角变化
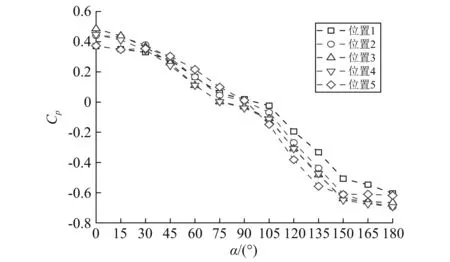
图3 不同位置光伏组件体型系数随风向角变化(β=10°)

图4 光伏组件体型系数随安装位置变化(β=10°)

图5 中间位置(位置3)光伏组件体型系数随风向角变化
2.2 组件表面风荷载分布规律
在进行光伏支架抗风设计时,应注意光伏组件表面风压分布不均导致弯矩对结构的不利影响[17],《光伏发电站设计规范》和《光伏支架结构设计规程》风荷载体型系数取值均采用均匀分布,该分布无法反应弯矩的影响。此外,《光伏支架结构设计规程》然采用均匀分布,但此规范考虑到组件表面风压分布不均的特点,也给出梯形分布风荷载体型系数参考值建议。图6(a)~(d)给出了倾角10°中间位置光伏组件在风向角分别为0°、180°、30°和150°时表面风荷载体型系数分布等值线图,可以看出,光伏组件表面风荷载并不是均匀分布,在0°和180°风向角下风荷载分布规律沿风向(y轴)表现明显的梯度,具有渐变性;在30°和150°风向角下风荷载分布规律沿风向同样表现出明显的梯度,此规律与光伏组件表面风压分布具有渐变性规律一致。另外,气流在组件角部“分离”与“再附”,造成角部漩涡比较复杂,但并不影响风荷载在组件表面渐变性的分布规律,并且,从等值线图可以发现,光伏组件迎风端所受风荷载大于背风端,文献[12]同样提到光伏组件顶部与底部风压大小不一致,风荷载作用在光伏组件表面会产生绕x轴和绕y轴的弯矩,在进行设计时需要考虑弯矩对结构可能产生的不利影响。由于组件表面风荷载分布规律明显,因此采用简化的风荷载分布模型表示组件表面风荷载是可行的。

图6 光伏组件表面体型系数分布(β=10°)
2.3 偏心风荷载分布
由于光伏组件表面风荷载分布不均,风荷载作用在光伏组件上的作用点偏离组件几何中心[18],可将风荷载等效为一组力和弯矩。风荷载通过光伏组件传递给上、下支撑索,作用在光伏组件风荷载FZ用体型系数Cp来表示,绕x轴弯矩Mx和绕y轴弯矩My分别用弯矩系数CMx和CMy来表示。x,y两方向偏心距定义为:
(6)
(7)
式中:XC和YC分别表示沿x和y方向偏离光伏组件中心O的距离。
弯矩直接影响上、下支撑索的受力和风荷载分配,图7和图8给出了不同倾角单排光伏组件和中间位置光伏组件两方向偏心距对比,可以看出,y方向的偏心距明显大于x方向,并且0°和180°风向角下x方向的偏心距基本接近于0,说明在0°和180°风向角下只存在绕x轴的弯矩(比较敏感),而绕y轴的弯矩几乎可以忽略,柔性光伏支架自身结构特性(长宽比较大)是造成绕x轴弯矩敏感性的主要原因。

图7 单排光伏组件两方向偏心距对比

图8 中间位置光伏组件两方向偏心距对比
3 风荷载体型系数和上、下支撑索分配系数取值建议
针对传统固定支撑单块光伏组件,马文勇等提出了偏心风荷载模型,该分布模型同样适用柔性支撑光伏组件,图9给出了柔性支撑光伏组件偏心距风荷载分布模型示意图,分析不同风向角下x和y两方向的偏心距,表1给出了风荷载体型系数和偏心距取值建议,偏心距是基于最大体型系数以及最大弯矩计算所得,值得说明的是0°和180°风向角并不特指某一个风向角,是对所有风向角进行统计的结果。

表1 风荷载体型系数及偏心距取值建议

图9 偏心距风荷载分布模型
光伏组件通过连接件固定在上、下支撑索上,结构简单,因此基于偏心风荷载分布模型可以得到风荷载分配到支撑索上的力系数。由于y方向的偏心距大于x方向,且在0°和180°风向角下x方向的偏心距基本为0,因此,为了方便结构设计,针对柔性太阳能光伏支架,仅考虑绕x轴的弯矩影响,得出力学关系如图10所示,从而获得分配到上、下支撑索的力。值得注意的是,其主要适用于柔性光伏支架(光伏组件由上、下索支撑,且倾角较小),对于支撑形式比较复杂的结构还有待进一步验证其适用性。
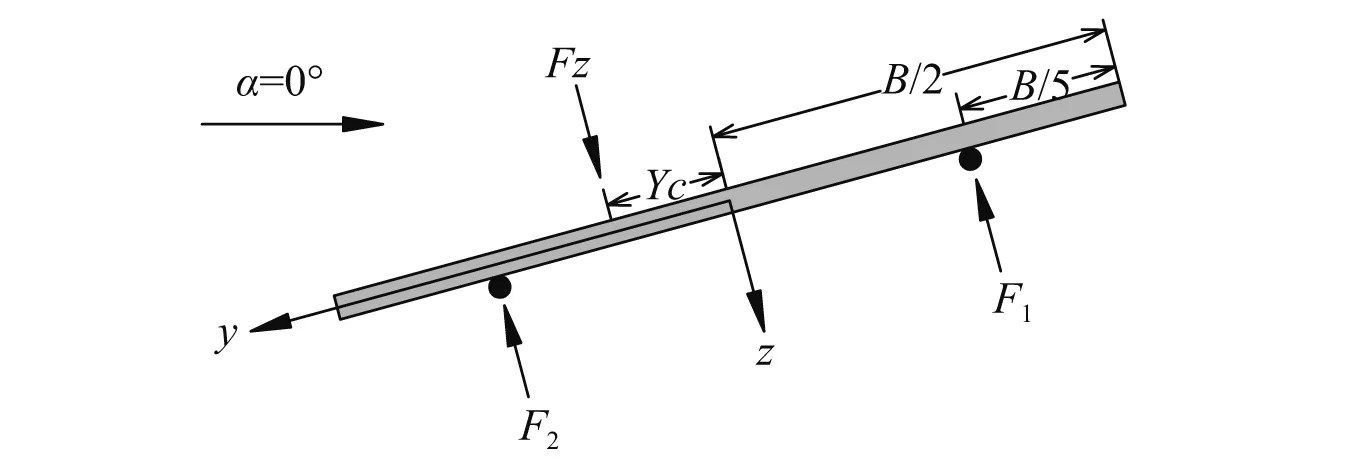
图10 力学关系示意图
基于刚性模型测压风洞试验结果,考虑整体风荷载和弯矩之间的关系,给出上、下支撑索计算公式:
F1+F2=FZ
(8)
(9)
表2给出了上、下支撑索风荷载分配系数取值建议,表中分配系数是依据上索距光伏组件顶部边缘B/5(下索距光伏组件底部边缘B/5)计算得到的,这主要是考虑到目前柔性光伏支撑索距光伏组件边缘距离一般在B/5以内以保证整体结构有较好的稳定性。当索距离光伏组件边缘更近时,表2给出的分配系数是偏于保守的。

表2 上、下支撑索风荷载分配系数取值建议
4 结 论
通过刚性模型测压风洞试验获得柔性支撑光伏组件表面风荷载分布规律,基于偏心风荷载分布模型计算上、下支撑索的风荷载分配系数。结论如下:
(1)柔性支撑光伏组件风压力极大值发生在0°或30°风向角附近,风吸力极大值发生在150°或180°风向角附近,因此,建议综合考虑150°和180°两个风向角,作为结构设计最不利荷载,且要考虑中间区域光伏组件风荷载较大的现象。
(2)柔性支撑光伏组件表面风荷载沿风向表现明显的梯度,具有渐变性,且光伏组件迎风端所受风荷载大于背风端,在进行柔性光伏支架抗风设计时,需要考虑偏心对结构的不利影响。
(3)小倾角柔性支撑光伏组件风荷载体型系数取值可以采用偏心距风荷载分布模型,基于偏心距风荷载分布模型获得上、下支撑索上分配的力,建议将柔性索固定在距离光伏组件边缘1/5长度范围内,采用本文考虑偏心距提出的风荷载分配系数分配上、下索力。
