改进的工况传递路径分析
2021-06-30廖旭晖戴旭东陈乐乐廖连莹孟浩东赵景波
廖旭晖, 戴旭东, 陈乐乐, 廖连莹, 孟浩东, 赵景波
(常州工学院 汽车工程学院,江苏 常州 213032)
当前,不管是在民用领域还是军用领域,振动和噪声问题都越来越受到重视,产品振动噪声性能的好坏往往直接关系到该产品的成败。传递路径分析(transfer path analysis, TPA)是一种面向问题(trouble shooting)的研究方法[1-2],能够帮助识别主要的振动和噪声的传递路径从而以此为依据对原结构加以改进。目前,TPA方法已经成为工程上解决振动噪声问题的重要手段。传统TPA的基本思想源于线性系统的叠加原理,在早期的许多文献中都已经有过这方面的论述。但是一般认为,最早应用“振源-路径-接受结构”的模型来研究工程中的振动问题应该追溯到20世纪80年代[3-5]。TPA为解决工程中的许多振动噪声问题提供了一种十分有效的解决方案,但是由于传统的TPA在实施过程中需要测量路径所传递的动态力以及被动侧的频响函数,所以存在测试效率比较低、测试过程比较繁琐等缺点[6]。为此,发展起来了一些改进的TPA方法。
在这些方法中,应用最为广泛的是工况传递路径分析(operational transfer path analysis, OTPA)[7-8]。OTPA是一种基于响应的传递路径分析方法,它通过建立目标点响应和参考点响应之间的联系来对传递路径进行分析。传递率是OTPA中的一个核心的概念,文献[8-10]中详细探讨了传递率的有关性质及测试方法。由于OTPA不需要测量力及频响函数,使得其测试过程相比于传统TPA大为简化。尽管OTPA实施起来比较方便,但也存在分析中容易遗漏路径、存在路径之间的相互串扰、传递率估计存在困难等问题[11-13],这些问题都会导致OTPA的测试精度的下降。为此,一些学者提出了一些改进的手段如利用奇异值分解(singular value decomposition, SVD)[14]、主成分分析(principal component analysis, PCA)[15]、独立分量分析(independent component analysis, ICA)[16]、正则化方法[17-18]等,来提高OTPA的测试精度。但是,OTPA对于路径的定义与传统TPA存在较大的差别,分析中容易造成对路径理解上的问题。为了解决这一问题并进一步改进OTPA的测试精度,本文提出了一种新的OTPA方法。所提出的改进方法主要是用主被动侧耦合点响应之间的差值来替代原先OTPA中的参考点响应信息,并结合SVD以及人工激励等手段,能够获得更高的测试精度及更清晰的物理意义。
1 传递路径分析的基本理论
1.1 传统的TPA
TPA理论将振动系统分成主动部分、传递路径和被动部分。激励力作用在主动部分上,通过若干条传递路径将振动传递到被动部分上。典型的TPA模型如图1所示。

图1 典型的TPA模型
被动部分上的目标点的响应可以看成是所有路径对该点响应的贡献之和。TPA的基本公式在频域可以表示成
(1)
式中:xi表示第i个目标点的响应,Fj表示第j条传递路径上传递的广义力,Hij表示力Fj到响应xi的广义上的频响函数。如果该路径是结构传播路径,Fj就是通常意义上的力。而如果该路径是声音的空气传播路径,Fj则表示体积声速。
根据TPA的基本理论,要想将目标点的响应完整地表示成各条振动传递路径的贡献量之和,需要进行两个方面的测试工作。一是测量被动部分的传递函数,也就是被动部分耦合点到目标点的传递函数。二是测量系统在工作时通过各条路径传递的动态力。在实际工程应用中,这两类物理量的测量都存在较大的困难。被动部分的传递函数的测量需要先将主动部分从耦合结构上拆卸下来,测试过程十分繁琐。而动态力的测量则需要在路径中安装力传感器,这在许多结构中几乎是不可能实现的,当然也可以采用动刚度法[19]和矩阵求逆法[20-22]来间接计算路径传递的动态力。
1.2 OTPA
设目标响应点集合记为A,参考点集合记为B,系统上的外力作用在自由度集合C上。当系统受到外力fC作用时,A和B上的响应向量可以分别表示成
xA=HACfC
(2)
xB=HBCfC
(3)
式(2),(3)中,HAC表示C到A的频响函数矩阵,HBC表示C到B的频响函数矩阵。
若HBC为列满秩矩阵,则由式(3)可以得到
(4)

(5)
令
(6)
式(5)变成
(7)
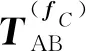
式(6)表示的是一般意义下的传递率矩阵。在TPA模型中,外力全部作用在主动部分上,并且通过路径传递到被动部分。就被动部分而言,每一条路径代表了一个作用力。为了更好地符合TPA的物理意义,通常对每一条路径选择一个参考点,可以将代表某条传递路径的参考点选取在被动部分与该路径的耦合点附近。这种情况下,就被动部分而言,外力的数量#C和参考点的数量#B都等于路径的数量,于是式(6)可以写成
(8)
根据式(7),可以将第i个目标点的响应表示成
(9)
式中,TAi Bk表示参考点Bk到目标点Ai的传递率。式(7)和式(9)就是OTPA的基本公式,显然式(9)和传统TPA基本公式(式(1))具有一致的形式。式(9)中的TAiBkXBk用来表示第k条传递路径对响应XAi的贡献。
3 OTPA的实施
3.1 传递率矩阵的测量
从OTPA的基本公式式(7)可以看出,在OTPA中只需要测量系统的响应以及参考点到目标点的传递率矩阵就可以了。系统响应可以通过加速度传感器在系统运行时很方便地测量得到,传递率矩阵可以通过以下方法计算得到。
可以将在系统运行时测量到的响应信号分成r组数据块,对于其中的每一个数据块都运用式(7)可以得到
(10)
式中的上脚标(i)表示测量的第i组数据块的频域信号。将式(10)合成起来得到
(11)
于是,传递率矩阵可以由下式计算得到:
(12)
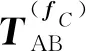

为了获得足够数量的不相关数据,可以特意地用不相关的激励源来对系统进行激励,从而获得不相关的响应量。一种简便易行的方法是所谓的人工激励法[23],即采用人工敲击的方式进行多次有效的激励并测量相应的工况数据。采用敲击的方式在主动侧进行人工激励时,每次改变敲击的位置,可以获得比较好的不相关数据,然后再将这些数据运用式(12)计算传递率矩阵就可以了。人工激励法主要是为了测量参考点到目标点的传递率,采用人工激励法也就将原先一步完成的测量工作变成了两步来完成。即第一步通过人工激励获取的数据来估计传递率,而第二步则获取实际工况下的数据并结合已经计算出的传递率来合成实际工况下的路径贡献量。
3.2 奇异值分解
式(12)实际上是一种利用最小二乘法来计算传递率的思路。这种方法虽然能够获得理论上的最优解,但是当参考点响应信号和测量噪声信号之间存在较高的相关性时,利用该方法估计得到的传递率将会存在较大的误差。这时,可以采用奇异值分解的方法来提高传递率矩阵估计的精度。
将参考点响应矩阵进行奇异值分解得到
(13)
式(13)中,U为#B×#B维酉矩阵(unitary matrix),V为r×r维酉矩阵,VH表示矩阵V的共轭转置。Σ为非对角线元素全为零的#B×r维矩阵,Σ的非零对角线元素称为矩阵XB的奇异值(singular values)。
由式(13)可以得到
(14)
及
(15)
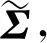
(16)
将式(16)代入式(12)就可以计算出传递率矩阵了。由于清除了信号中的一些噪声成份,利用奇异值分解方法计算得到的传递率矩阵具有更高的精度。
4 改进的OTPA
从前面的分析可以看出,OTPA虽然测试过程比较简单,但是精度有限。尤其是用参考点响应对目标点响应的贡献替代了路径贡献量的概念,这在物理意义上来说,与传统的TPA是有偏差的。本文在这里介绍一种改进的方法,该方法仍然使用工况数据,其实施过程与OTPA相仿,但是物理意义和传统的TPA更为接近。
可以将TPA模型中的每条传递路径看成是一个线性弹簧,其中第j条传递路径所传递的工况力在频域内可以表示成
Fj=Zjδj
(17)
其中,
(18)
式(17)中,Zj表示第j条传递路径的动刚度。式(18)中,δj相当于第j条路径的变形量,aaj表示路径与主动侧耦合点的加速度响应,apj表示路径与被动侧耦合点的加速度响应。
将式(17)代入式(1)得到
(19)
令
Tij=HijZj
(20)
式(19)于是可以写成
(21)
式中,Tij表示从δj到yi的传递率。式(21)就是改进的OTPA的基本公式。显然,式(21)将目标点响应看成是由各条路径的变形所导致的。由于该式是由传统的TPA推导得出的,所以改进的OTPA中的路径贡献量具有跟传统的TPA中相同的物理意义,这一点是有别于OTPA的。很显然,式(21)中的Tijδj就表示第j条路径上的力而非响应对第i个目标点的响应贡献量。但是,改进的OTPA又借鉴了响应传递率的概念,改进的OTPA中的传递率Tij从本质上来说仍然是一种“响应-响应”传递率而非“力-响应”传递率(即通常意义上的频响函数)。因此可以通过与OTPA中计算传递率相似的步骤来计算路径变形量到响应的传递率。
将式(21)表示成矩阵的形式如下:
yA=TyAδδ
(22)
其中,
δ=[δ1,δ2,…,δN]T
(23)
δ表示由路径变形量构成的列向量,TyAδ表示路径变形量到目标点响应的传递率矩阵。N表示总的路径数量。
在OTPA中测量的工况数据为参考点的响应,而改进的OTPA中则需要测量路径与主动侧和被动侧的耦合点的响应,从而获取路径变形量信息。计算路径变形量到目标点的传递率矩阵可以由下式计算得到:
(24)
式(24)中,上脚标(i)表示测量得到的第i组数据块的频域信号。可以看出,改进的OTPA方法与传统的OTPA的实施步骤是基本相同的。上一节所介绍的人工激励法、SVD等也都可以用于改进的OTPA中。使用人工激励的方式来实施改进的OTPA同样分为两个步骤:第一步,在主动侧实施激励的同时测量主被动侧耦合点以及目标响应点的响应,并利用式(24)计算传递率。第二步,在系统实际工作时测量以上响应并利用式(21)计算各路径贡献量。
值得指出的是,改进的OTPA与另外一种工程实践中常用到的传递路径分析方法——扩展的工况传递路径分析(operational path analysis with exogenous inputs,OPAX)[24-25]在测试过程和物理意义上都有相似之处。OPAX同样也需要测量主被动侧的响应,然后利用参数化模型来识别悬架的动刚度,进而计算出路径传递的动态力的大小,但OPAX仍然需要对被动侧的频响函数进行测量。而改进的OTPA只关注路径动态力对目标点响应的贡献而并不关注路径动态力本身,因此不需要测量被动侧频响函数,这使得测试过程大为简化。而关于路径贡献量的物理意义,改进的OTPA和OPAX都与传统的TPA比较接近。
5 实验研究
5.1 实验方案
本节通过实验来研究并比较几种TPA方法。所用到的实验模型如图2所示,该模型类似于一个“发动机-车架”振动传递模型。模型细节如图3所示,上面一层结构为主动部分,相当于发动机;下面是被动部分,相当于车架;中间有3条振动的传递路径,相当于3个发动机悬置。实验中的激励均为Z方向(垂直地面方向),三条传递路径也是沿Z向,所使用的实验结构的振动也以该方向为主,因此只关注在该模型Z方向上振动。

图2 用于TPA的实验模型

图3 实验模型细节
所进行的实验及具体实验方案如下:
(1) 传统的TPA
传统的TPA需要两个步骤。第一步是测量被动部分的频响函数。在测量被动部分的频响函数时,需要首先将主动部分及路径拆除,然后用锤击法进行频响函数的测量。由于被动部分结构的耦合点处有安装孔,敲击存在一定的困难,因此在本文中利用互易性原理进行频响函数的测量,所选取的目标响应点如图2所示。所测量的三个悬置连接点到目标响应点的频响函数如图4所示。第二步则需要测量工况下的路径传递力。为了精确测量振动过程中通过路径传递的力,在模型的每条路径中串联了一个力传感器,力传感器的安装位置如图5(a)所示。由于只是验证性试验,对工况没有太多的要求,本文中采用人工敲击的简单激励方式在主动部分进行激励,目标点的时域响应信号如图6所示。与此同时,测量路径上传递的力以及目标响应点的响应,力传感器所测量得到的三条传递路径上的力的频域信号如图7所示。最后利用TPA的基本公式式(1)来计算每条路径对目标点响应的贡献量,并将所有路径贡献量合成的结果与直接测量得到的结果进行比较。

图4 测量得到的被动侧频响函数

图5 传感器布置位置

图6 目标点的时域响应信号

图7 测量得到的路径动态力
(2) OTPA
首先选取被动部分上的三个耦合点作为参考点,通过人工激励的方式在结构的主动侧进行激励并获取参考点和目标点处的响应信息。利用3.1节计算传递率的方法计算参考点到响应点的传递率,所计算得到的参考点到目标点的传递率如图8所示。最后,进行工况下响应的测量,并利用OTPA的公式计算该工况下每条路径的相应贡献量。

图8 各参考点到目标点的响应传递率
(3) 改进的OTPA
改进的OTPA中不仅要测量被动部分耦合点的响应,还需要测量主动部分耦合点的响应,传感器的布置方式如图5(b)和(c)所示。利用OTPA中计算传递率相同的方法计算路径变形量到目标点响应的传递率(如图9所示)。最后,进行工况下响应的测量,并利用改进的OTPA的公式计算该工况下每条路径对响应的贡献量。
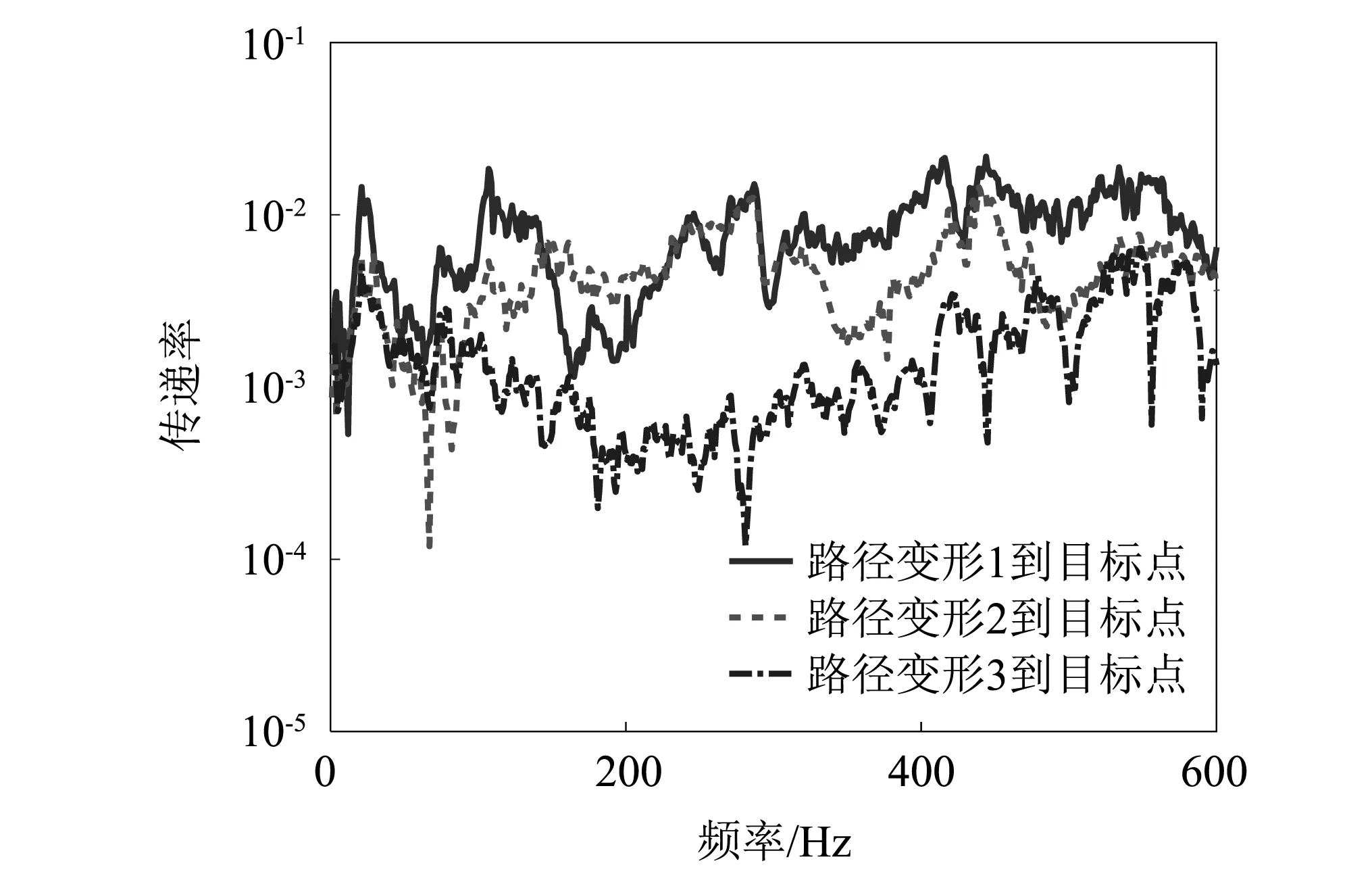
图9 各路径变形量到目标点的响应传递率
上面三个实验都需要两个步骤才能完成,即路径特性的测量和工况数据的测量。但是,上述三个实验所需要的工况数据需要在同一次测量中获取,这样可以比较同样工况下三种TPA的结果之间的差别。而上述的第(2)个实验和第(3)个实验中用于计算传递率的有关测量也可以在一次试验中同时完成。因此,上述三个实验总共需要三个步骤:①测量被动部分耦合点到目标点的频响函数,所测得的数据用于传统的TPA。② 采用人工激励法,测量耦合点和目标点的响应,通过测得的响应数据估计传递率。③测量工况数据,包括工况下的响应和路径力并计算路径贡献量。
5.2 实验结果分析
首先分析传统TPA的实验结果。图10显示了三条传递路径对参考点响应的贡献量之和与直接测量的该点响应的比较,从图中可以看出两条曲线十分接近,验证了所用方法的正确性以及测量的准确性。

图10 直接测量与合成得到的参考点响应比较
图11显示了在传统TPA中得到的每条路径的贡献量情况。由于传统TPA中每一条路径的贡献量是直接测量得到的,一般认为是比较准确的结果。因此,会将该计算结果用于跟另外两种方法所计算得到的结果进行比较,分析另外两种传递路径方法的准确性。
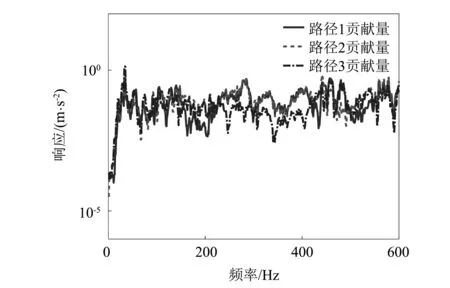
图11 传统TPA得到的路径对目标点响应的贡献量
为了比较的方便,将三种方法分析的每一路径的贡献量绘制在同一张图上。计算得到的路径1~路径3的贡献量分别如图12(a)~(c)所示。从图中可以看出,三种方法中改进的OTPA与传统的TPA的结果更为接近。而OTPA由于路径的定义和传统的TPA有本质的区别,再加上该模型中阻尼较小,路径之间的串扰效应比较明显,使得OTPA与传统的TPA结果差别比较大。结果表明,改进的OTPA能够在一定程度上改善OTPA的路径串扰的问题,从而提高OTPA的精度。

图12 三种TPA方法分析结果比较
6 结 论
本论文对OTPA方法进行了综合的论述,提出了一种改进的OTPA方法,以提高传递路径分析中的测试精度。主要结论如下:
(1) 提出了一种改进的OTPA方法,该方法利用上下悬置点响应的差值而不是被动侧参考点响应来合成目标点的响应。改进的OTPA可以改善工况传递路径分析的路径串扰的问题,从而提高OTPA的分析精度,而且改进的OTPA的物理意义与传统TPA也更为接近。
(2) 本文所提出的方法和OTPA的操作流程基本相同,传递率的测量是OTPA中的关键步骤,可以利用工况数据来计算传递率。在改进的OTPA中,同样可以利用人工激励及SVD等手段来提高传递率的计算精度。
