移动下击暴流作用下输电塔的风振响应及荷载评估方法
2021-06-30孙启刚宋卓彦汪大海
赵 勇, 孙启刚, 宋卓彦, 汪大海, 王 昕
(1.国网山东省电力公司,济南 250000;2.国网山东省电力公司经济技术研究院,济南 250000;3.武汉理工大学 土木工程与建筑学院,武汉 430070)
下击暴流为雷暴天气中强下沉气流撞击地面后向四周扩散而引起的冲击性近地面强风[1]。该风场持续时间较短,作用范围较小,直径可小于4 km,但风速较高,可达40~50 m/s,最大风速位于距离地面高度30~80 m处[2]。输电线路往往绵延数百公里,其遭遇雷暴风作用的概率较大,加之塔线耦联结构具有柔度大、阻尼小的特点,本身就对风荷载较为敏感。在我国,由下击暴流风荷载导致的输电杆塔的倒塌事件常有发生:2005年6月14日,江苏泗阳500 kV任上5237线遭到下击暴流袭击,导致10基输电塔倒塌,造成大面积的停电[3]。2009年7月24日,河北南部遭遇雷暴风,造成500 kV辛彭线8基输电塔倒塌[4]。2011年7月27日,110 kV园江线41号、42号塔发生倒塔事故,现场23基低压电杆被连根拔起,风灾倒塔致使数十条10 kV线路断电[5]。2013年,8月7日,聊城、德州、济南、滨州自西向东发生雷暴风灾害,造成当地配网大面积破坏,500 kV聊长线多次跳闸。
为研究下击暴流的风场特性,国内外学者展开了大量的研究。建立下击暴流的解析模型能够快速简便的模拟下击暴流风场。Vicroy[6]在Oseguera和Bowles[7]模型的基础上提出了OBV模型,重新定义了风场的径向形状函数,使得解析模型更接近实测风速剖面。Holmes和Oliver模型[8]修正了水平风速沿径向距离变化的规律,得到更为准确的径向形状函数。Li等[ 9]考虑了边界层厚度呈非线性增长的特征,对OBV模型的竖向形状函数和径向形状函数进行修正,完善了下击暴流风场三维平均风速的空间表达方式。Abd-Elaal等[10]等又进一步完善了水平风速的径向和竖向风剖面函数。风洞试验是研究下击暴流风场特性和下击暴流作用下结构特性的重要试验方法。赵杨等[11-12]通过风洞试验的方式来模拟下击暴流,并对该风场作用下高层结构的风压分布特性进行了具体研究。Elawady等[13]在西安大略大学的WINDEEE三维风洞装置中模拟并测试了下击暴流风场,并通过输电线路的气弹模型开展了动力响应的试验分析。
近年来,国内外研究学者对下击暴流作用下输电塔的风振响应和破坏特征开展了大量的研究。Shehata等[14]通过对输电塔结构进行弹性静力分析,研究了不同参数的下击暴流风荷载作用下输电塔杆件内力的变化趋势。王昕等[15]基于半确定性随机混合模型,通过有限元建模,比较了下击暴流和良态风作用过程中输电塔的受力特征。吉柏锋等[16]对输电塔线结构进行动力时程计算,研究了输电塔杆件失稳破坏导致结构倒塌的全过程。杨风利等[17]采用典型国际规范的风荷载取值,考察了下击暴流作用下输电杆塔的破坏模式。李宏海等[18]基于壁面射流理论,通过流体动力学模拟(CFD)研究了棱柱结构和开敞式屋盖结构表面的风压变化及风荷载分布。徐挺等[19-20]通过调节平板位置研究了稳态下击暴流水平风速剖面参数对于输电塔风振响应的影响。Aboshosha等[21-22]给出了输电线路导线在下击暴流荷载作用下结构反应的一个半解析解,并通过有限元分析验证了该方法的准确性,且通过研究下击暴流的参数变化对输电线路的影响,确定了三种临界荷载的情况。上述研究大多分析了下击暴流作用下输电线路的风振响应特性,但对于下击暴流作用下输电塔的风荷载的评估方法鲜有涉及。
本文采用下击暴流场的平均风Li等模型和Chen等[23]的脉动风速理论,模拟了移动下击暴流作用下输电杆塔的风荷载时程。通过建立输电塔的空间有限元模型,研究了移动下击暴流平均风、拟静力和瞬态动力三种工况作用下输电塔在频域及时域内风振响应的规律,考察了移动下击暴流时变平均风作用下的最不利风剖面。同时,按照非平稳随机振动的极值分析理论,基于“风振惯性力”方法,给出了最不利风剖面作用下输电塔脉动风振响应的等效静力风荷载分布,并与动力有限元分析结果进行对比和验证。提出了下击暴流作用下输电塔风荷载的评估方法。
1 下击暴流风场模型
1.1 时变平均风场
考虑到下击暴流的移动,风场中任一位置点的风速U(z,t)表示为:

(1)
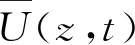

(2)
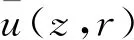
(3)
式中:uVS(z)为最大水平风速沿竖向的风剖面形状函数,可表示为公式(4);uRS(r)为水平风速沿径向的风剖面形状函数,可表示为公式(5);um为下击暴流最大水平风速。uVS(z)以及uRS(r)曲线见图1。
(4)
式中,γ=0.159;zm=0.039 3D为最大水平风速出现的高度;D为风场射流直径。
(5)
式中:β=1.287;Rc为风场径向尺度,可取为0.599rm;rm=0.007 8D,为最大水平风速出现的直径。
由于边界层厚度呈非线性增长,不同高度位置处的水平风速最大值uRS(rm)对应的径向距离rm不同。因此,Li模型对OBV模型的水平风速沿径向的风剖面形状函数进行了完善,给出了rm与高度z的关系:
(6)
式中,η=2.01;χ=-0.036 3。曲线如图1所示。

图1 竖向和径向形状函数
式(2)中,u(z)为射流中心移动导致的下击暴流的平均风速增量,Chen等认为其沿高度的变化趋势与uVS(z)相同,且射流中心的移动速度ut=max(u(z)),故u(z)可表示为:
u(z)=uVS(z)ut
(7)
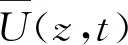
(8)
1.2 随机脉动风场
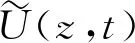

(9)
式中:k(z,t)为一均值为0,方差为1的平稳高斯过程,其功率谱密度函数可表示为:
S0(z1,z2,n)=S0(n)coh(z1,z2,n)
(10)
式中,n为频率(Hz);S0(n)可采用归一化的脉动风Davenport谱:
(11)

(12)
式中,衰减因子可取C=16。与边界层良态风类似,下击暴流脉动风速的均方根σ(z,t)可视为沿高度不变,表示为:
(13)
式中,I10为10 m高度处湍流度,参考文献[27],B类地貌可取I10=0.14。定义非平稳一致调制函数a(t)为:
(14)
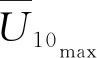
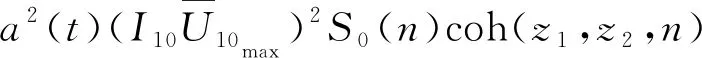
(15)
2 杆塔结构的有限元建模及风荷载计算
本文以华东平原地区一典型500 kV格构式猫头输电塔为分析对象,塔高48.5 m,呼高39 m,主材为角钢,塔体钢材均采用Q345钢,该塔在我国的输电工程应用中具有一定的代表性。
输电塔的建模、动力特性分析以及下击暴流风振响应分析均在ANSYS有限元分析软件环境中进行。选取空间三维薄壁梁单元BEAM188模拟杆塔的角钢杆件,该单元的特点在于可以考虑L型开口薄壁截面所特有的翘曲变形。杆塔有限元模型中共有1 299个单元。在进行风振动力响应计算之前,先对杆塔结构的动力特性进行分析。表1给出了输电塔前四阶振型频率及振型描述,图2给出了对应的振型示意图。
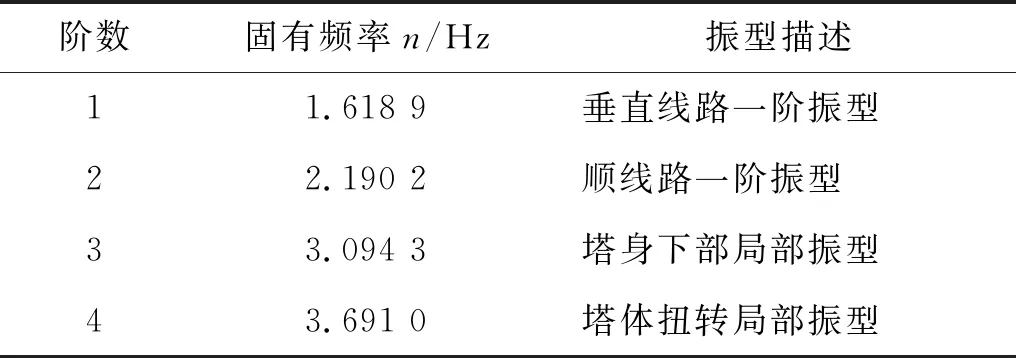
表1 塔体模型的自振频率和振型描述

图2 输电塔前四阶振型
根据每段塔段质量接近的原则,在高度方向上将输电杆塔共划分成八个塔段,取每个塔段内塔身主杆和塔身斜腹杆的节点处为风速加载点,如图3所示。下击暴流作用于输电杆塔的方式如图4所示。
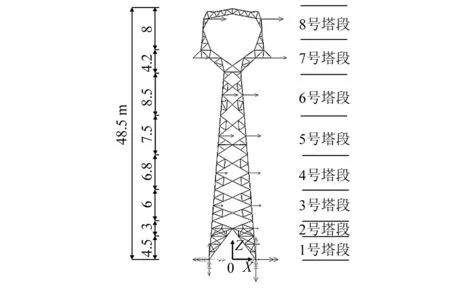
图3 输电杆塔模型及加载方式示意图
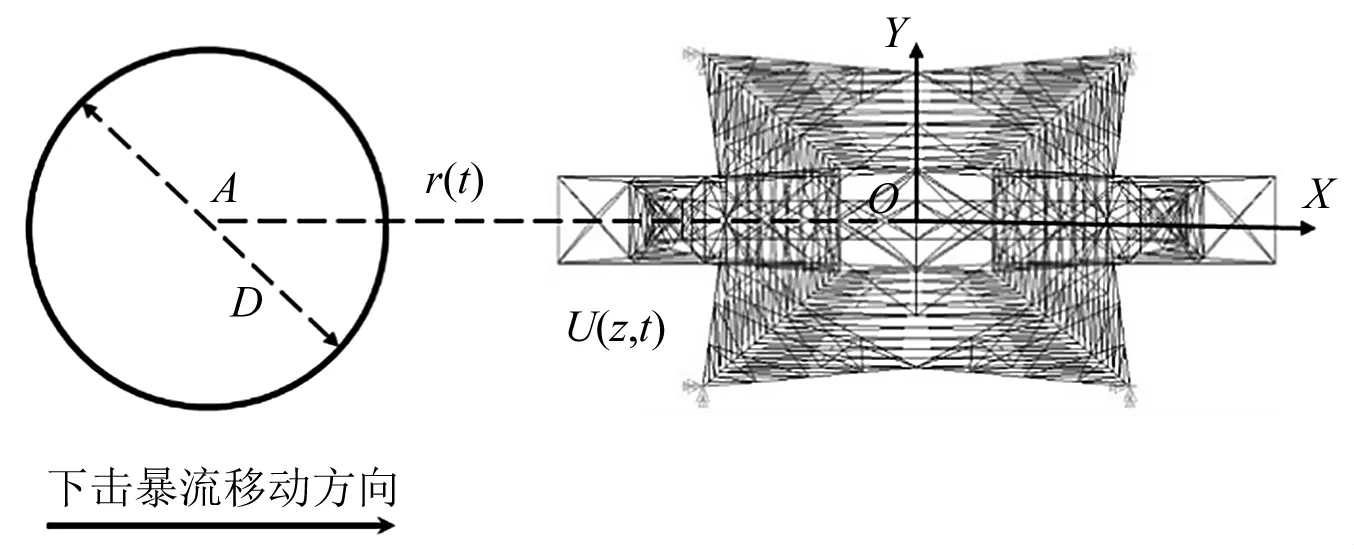
图4 下击暴流作用于输电杆塔示意图
该输电线路大部分位于乡村的空旷地区,属于B类地貌。本文参照文献[22],取下击暴流最大风速um=45 m/s,射流直径D=800 m,移动风速ut=12 m/s,移动方向取为垂直于线路方向。下击暴流中心初始位置距离杆塔中心的径向距离r0=3 600 m。同时,依据1.2节脉动风速模型,采用谱表现法可进行随机脉动风场的模拟[25-26]。
综合时变平均风和非平稳脉动风,图5中给出了下击暴流冲击下杆塔的1号、5号及8号三个加载点的模拟时变平均风速时程和非平稳脉动风速时程。依据准定常方法,作用在高度zi处杆塔加载点的风荷载可表示为:
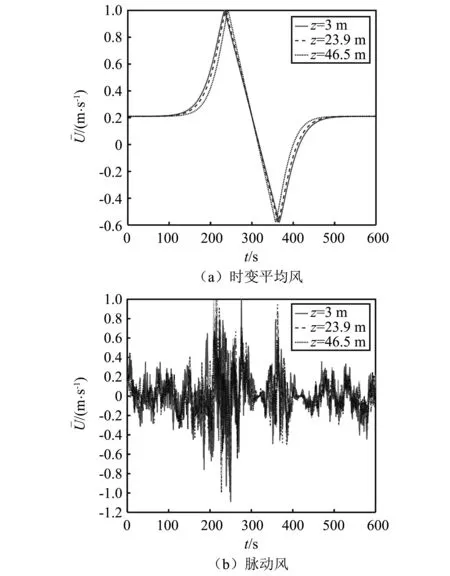
图5 下击暴流风速的归一化时程
F(zi,t)=μs(zi)*As(zi)*wi(zi,t),i=1,2,…,8
(16)
式中:μs(zi)为高度zi对应塔段的风载体型系数,可按我国规范取值[27]。As(zi)为该塔段的迎风面投影面积,wi(zi,t)为zi高度处的风压,采用下式得到:
(17)
式中,ρ为空气密度,ρ=1.29 kg/m3。U(zi,t)按照公式(1)进行计算。
3 移动下击 暴流下杆塔的风振响应
通过对输电杆塔施加如下三种移动下击暴流工况的荷载,研究杆塔的风振响应变化规律:
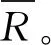
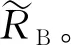
工况C:通过多步瞬态动力计算,分析移动下击暴流冲击作用全过程的杆塔的动力响应,结构阻尼取为1%,下文记为R。
3.1 时变平均风响应
在移动下击暴流冲击输电杆塔的过程中,暴流中心从初始位置先不断向杆塔接近,然后远离。期间随着暴流中心与杆塔的径向距离r(t)变化,下击暴流作用在杆塔的竖向风剖面也随之发生变化。本算例中,t=200~300 s的时间段内,下击暴流中心到输电杆塔中心的径向距离由r=1.5D逐渐变为r=0,图6给出了作用于杆塔上的平均风竖向风剖面在此期间的变化情况。
由图6可知,当t=240 s,径向距离r=0.9D时,该时刻风剖面的最大风速值达到了包络风剖面的最大值,且风剖面上最大风速点高度也随着最大风速值的增大而增高。之后,随着r(t)减小,风速也开始逐渐减小,当t=300 s时,下击暴流中心与输电塔中心重合,此时径向距离r=0,竖向风剖面仅含风场移动速度。

图6 杆塔上时变平均风的竖向剖面
随着时变平均风剖面的变化,结构平均风静力响应也随之变化。对结构响应采用R/Rmax进行归一化处理,图7给出了输电杆塔基底剪力、基底弯矩、塔顶位移和杆件轴力与径向距离r/D之间的关系。可以看出,结构响应先增大后减小,当风场运动到t=235 s左右时刻出现来流(正向)极值;在下击暴流中心穿过输电杆塔然后远离的过程中,结构响应在t=360 s左右时刻出现去流(负向)极值。冲击全过程中,最大响应出现在来流阶段。
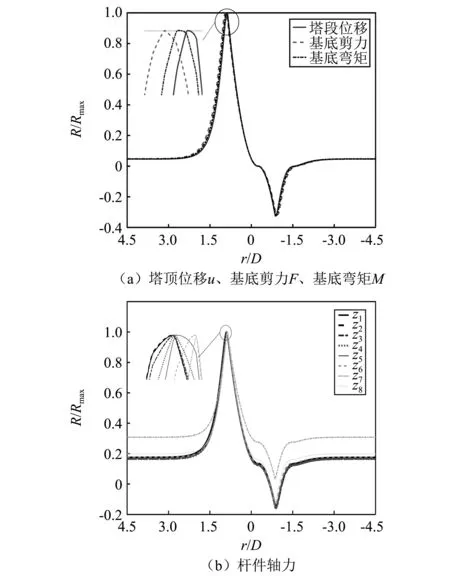
图7 杆塔响应随径向距离的变化
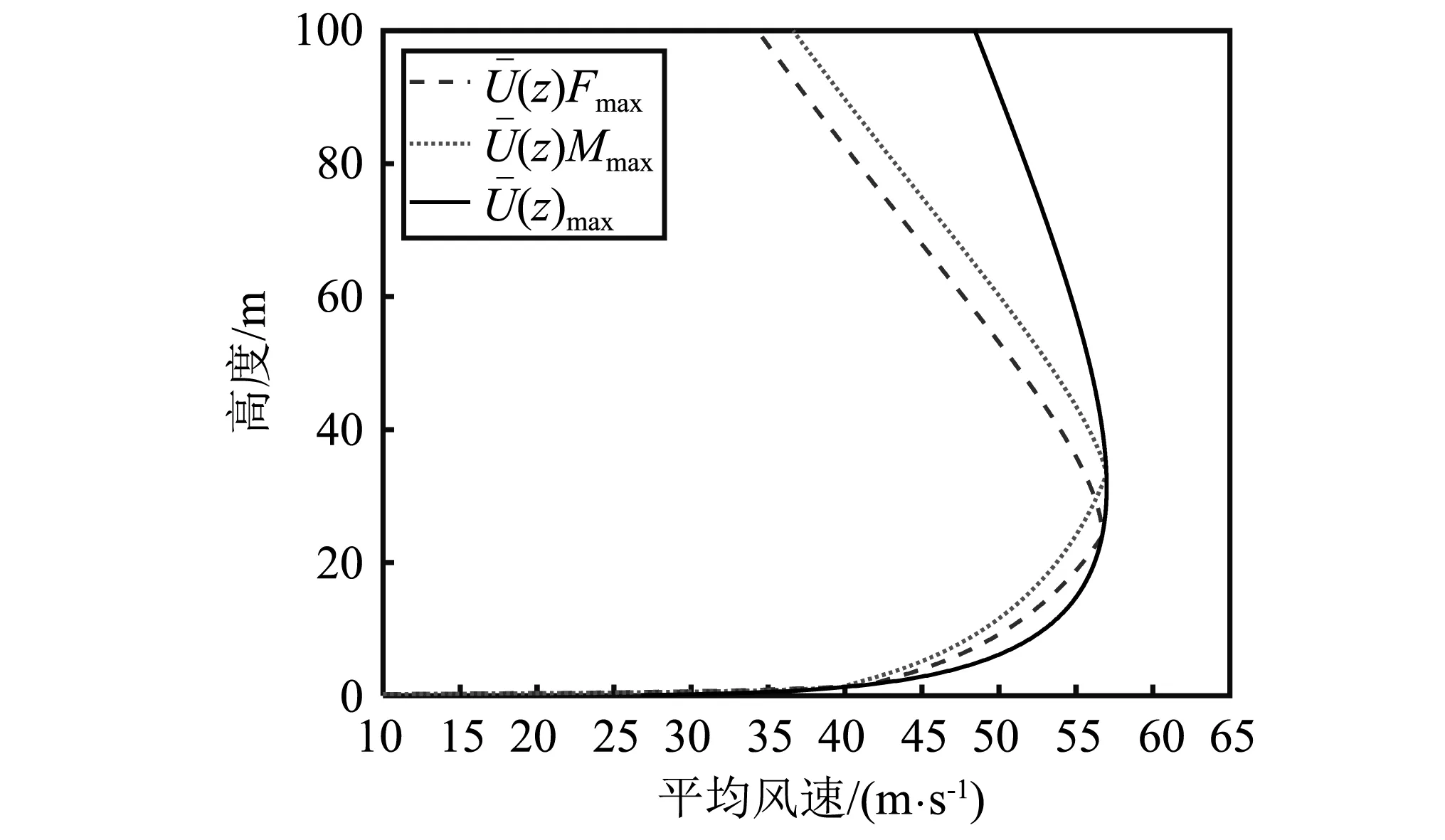
图8 响应最大时刻的平均风速剖面


表2 最不利平均风剖面风作用下输电塔响应对比

图9 最不利平均风剖面荷载,最不利平均风剖面下内力与时变平均风下最大内力比较
综合比较上述三种最不利平均风剖面下各类结构响应可以发现,U(z)max的结果均能包络住时变平均风响应的最大值,且偏差在10%以内。又U(z)max分布情况与响应类型和杆塔高度无关,因此具有良好的适用性,可作为移动下击暴流时变平均风作用下输电杆塔响应理想的最不利设计风剖面。
则最大时变平均风荷载Fmax(zi),可以表示为:
(18)
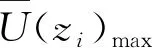
(19)
w0为10 m高度处的最大时变风压,可以表示为:
(20)
3.2 脉动风响应

(21a)
(21b)
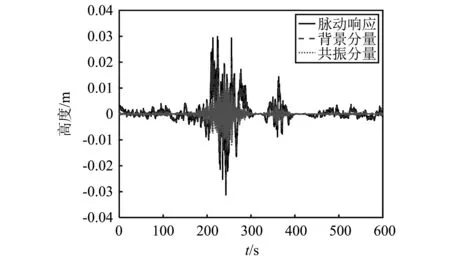
图10 塔顶位移各分量时程图
由图10可知,脉动响应及其背景分量和共振分量均表现出明显的非平稳特征。塔顶位移时程中脉动部分绝对值最大为0.031 m,其中背景响应为0.021 m,共振响应为0.015 m。采用小波分析得出的时频图能够明确显示脉动风非平稳响应中能量频谱分布特征。图11给出了塔顶位移脉动响应及其背景和共振分量的时频图。
由图11可知,在时间维度上,200~250 s和350~400 s两时间段内分别出现了来流峰值和去流峰值,且第一峰值段较第二峰值段能量高。由于非平稳脉动风和时变平均风具有相同的调制函数,故对比图7和图11可发现平均风和脉动风振响应峰值的时刻相一致。在频率维度上,通过对比图11(b)和(c)可以发现,脉动响应在低频段的能量较高,表明脉动响应主要是背景分量的贡献,背景分量显著高于共振分量。这一点亦和图10中时程分析中得出。在高频段,脉动响应能量出现两处集中的峰值,分别为来流和去流过程中共振分量。两个峰值对应的频率与前述动力特性分析的结构模型一阶固有频率n1=1.6 Hz相吻合,说明共振响应以一阶振型贡献为主。

图11 塔顶位移时频图
上述时频分析表明,下击暴流作用下杆塔的脉动风振响应与平稳良态风振动响应表现出同样的特征:均以背景分量为主,且共振分量都以一阶模态为主[27-28]。二者的差异在于前者具有显著的非平稳特性。基于非平稳随机振动理论,当响应为演化高斯随机过程时,响应的极值概率分布[29]可以表示为:
(22)

(23)

(24)
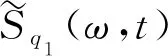
(25)
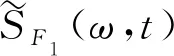
(26)
式中,SF1(ω)为未经调制的平稳风作用下的一阶振型广义力荷载谱,可表达为:
As(zi)As(zj)φ1(zi)φ1(zj)
(27)
式中各个系数符号意义均与前述一致。则塔顶位移的均方根值σu(t)可表示为:
σq1(t)=a(t)σq1s
(28)
式中,σq1S为采用同样脉动风场参数的未经调制的平稳风作用下的一阶振型广义位移功率谱。
(29)
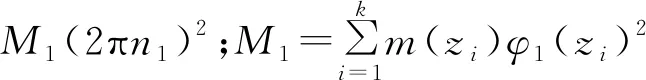
(30)

3.3 全风响应

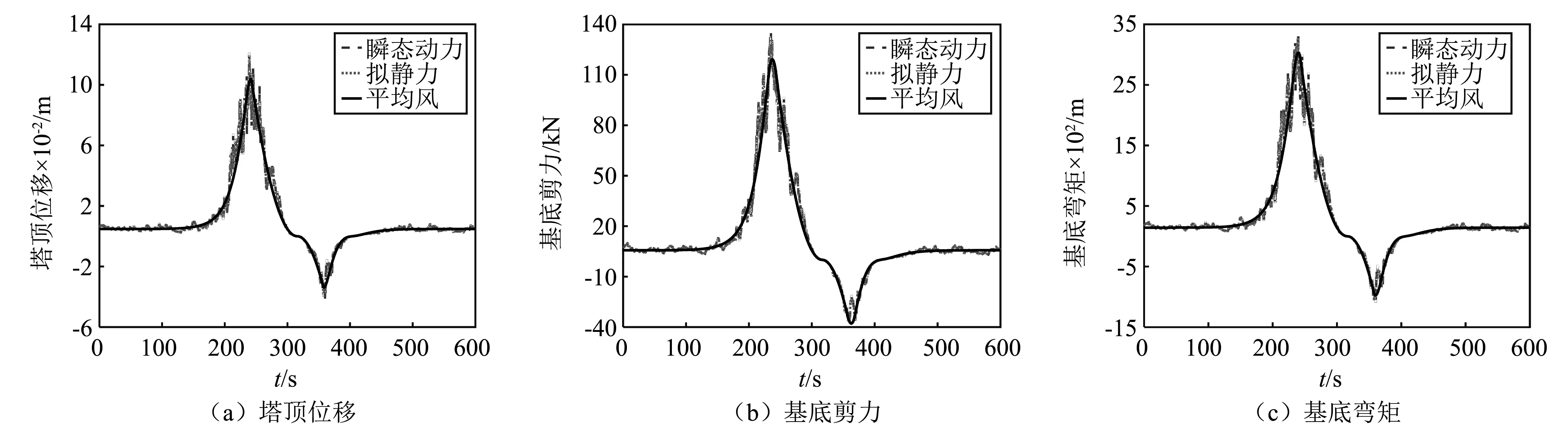
图12 三种工况下输电杆塔响应时程

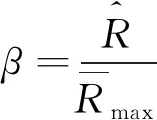
(31)
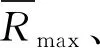

表3 移动下击暴流下杆塔内力风振系数β
由表3可知,拟静力工况和瞬态动力工况下,塔顶位移、基底剪力和基底弯矩响应,以及各杆件内力响应的风振系数均在1.2左右,表明时变平均风的贡献在全风作用中占到了主要。由于振型分布的影响,杆件内力风振系数随高度增大。
同时,分别根据平均风、拟静力和瞬态动力作用下输电塔杆件轴力时程,可得到各杆件内力最大值随高度的分布,如图13所示。各类响应均表明,时变平均风效应占到全风动力作用的主要部分。由于拟静力效应的实质为平均风和脉动风振响应背景分量之和,且背景分量是脉动风作用的主要贡献部分,全风下的拟静力作用和瞬态动力作用接近。这也与目前各国输电杆塔设计风荷载规范中可只需考虑背景分量的结论一致。
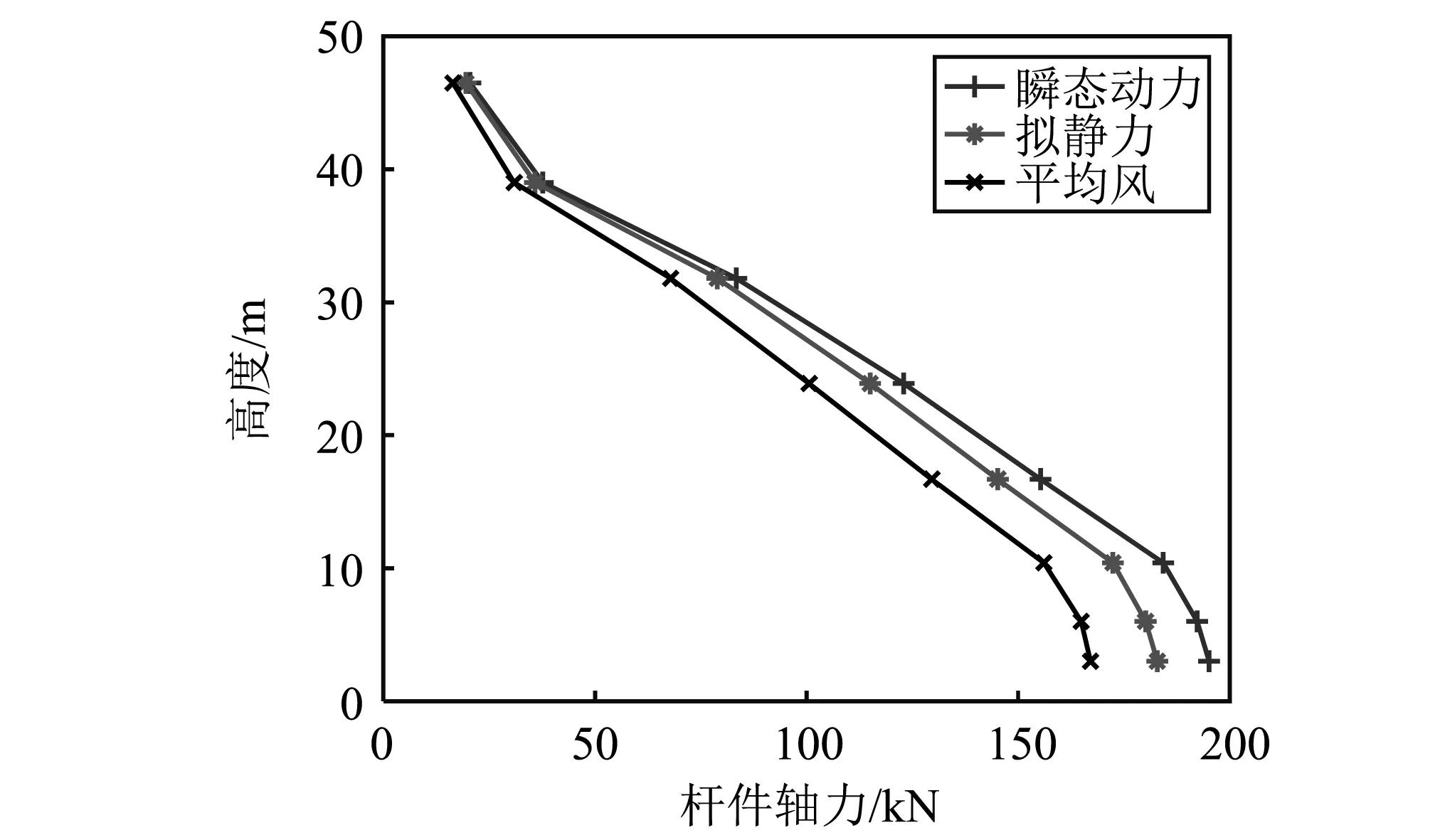
图13 三种工况下输电塔杆件轴力最大值
4 等效静力风荷载
(32)
结合前述第3节最不利平均风剖面讨论,移动下击暴流作用下的设计风荷载公式可表示为:
(33)
式中,最大平均风荷载Fmax(zi)已经在式(18)中给出。

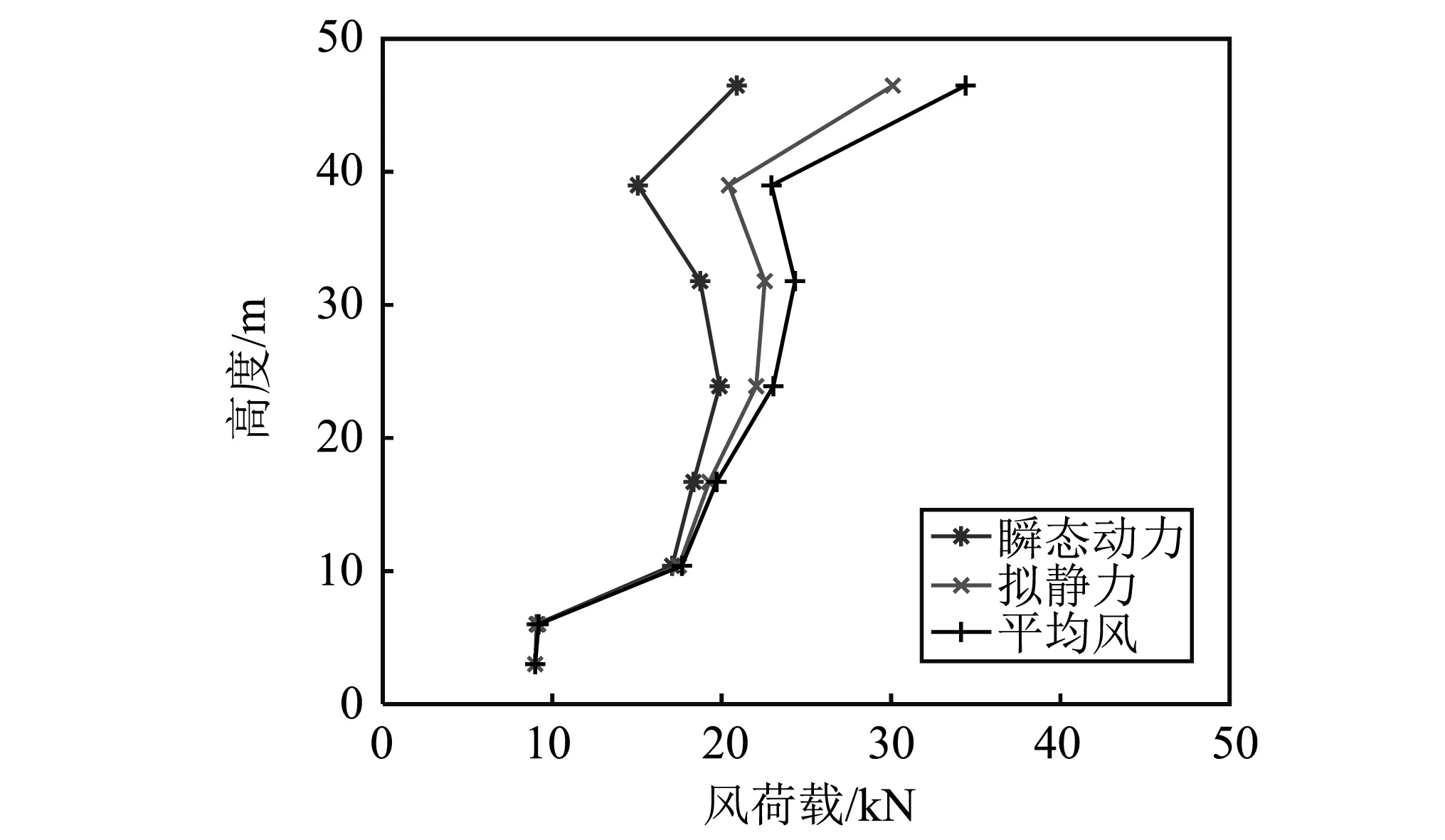
图14 等效静力风荷载分布
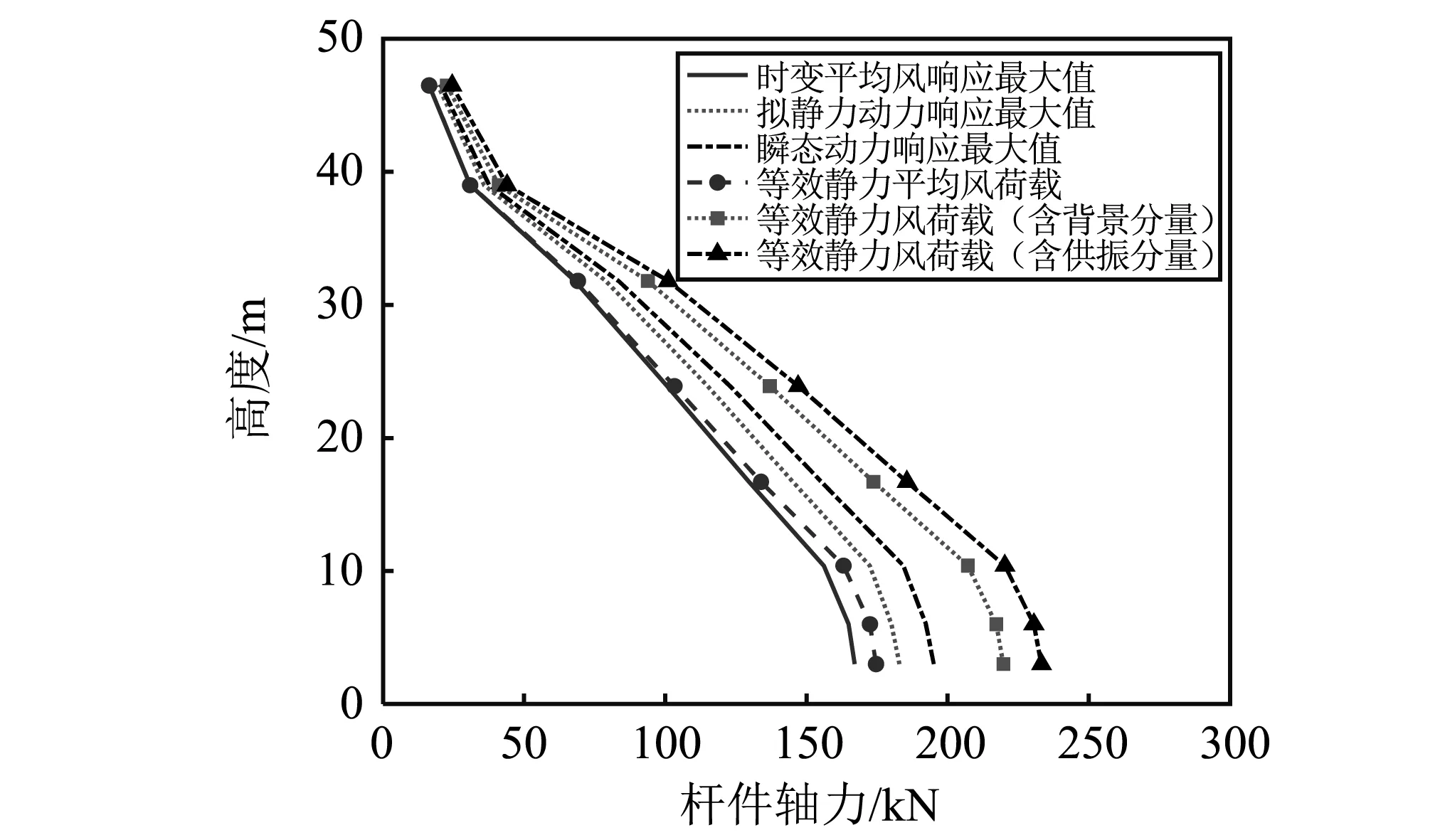
图15 等效静力风荷载与时程分析的塔段内力比较
由图15可知,等效静力风荷载中的平均风荷载效应与时变平均风效应吻合很好。在考虑极值响应的等效静力风荷载作用下,各杆件轴力均包络住时程分析作用下响应的最大值。且由于杆塔为悬臂高耸结构,上部荷载的偏差会逐步向底部累积,造成底部的杆件内力偏大,最大偏差可以达到18%。
从表4和表5中可以发现,与杆件内力响应的情况相似,在平均风作用下,等效静力风荷载计算的结构响应略大于时变响应最大值,但两者在拟静力和瞬态动力作用下的杆件轴力响应偏差有所偏大。各类响应最大偏差在20%以内。
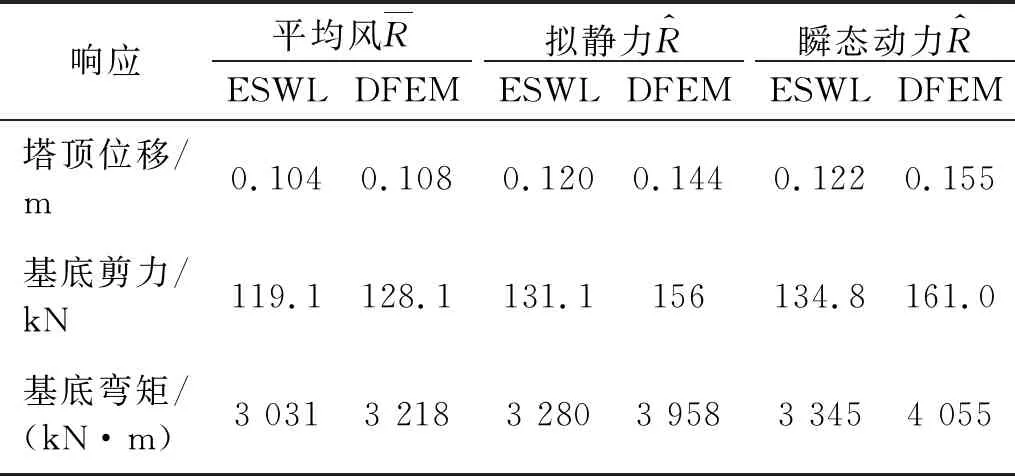
表4 输电塔整体响应对比
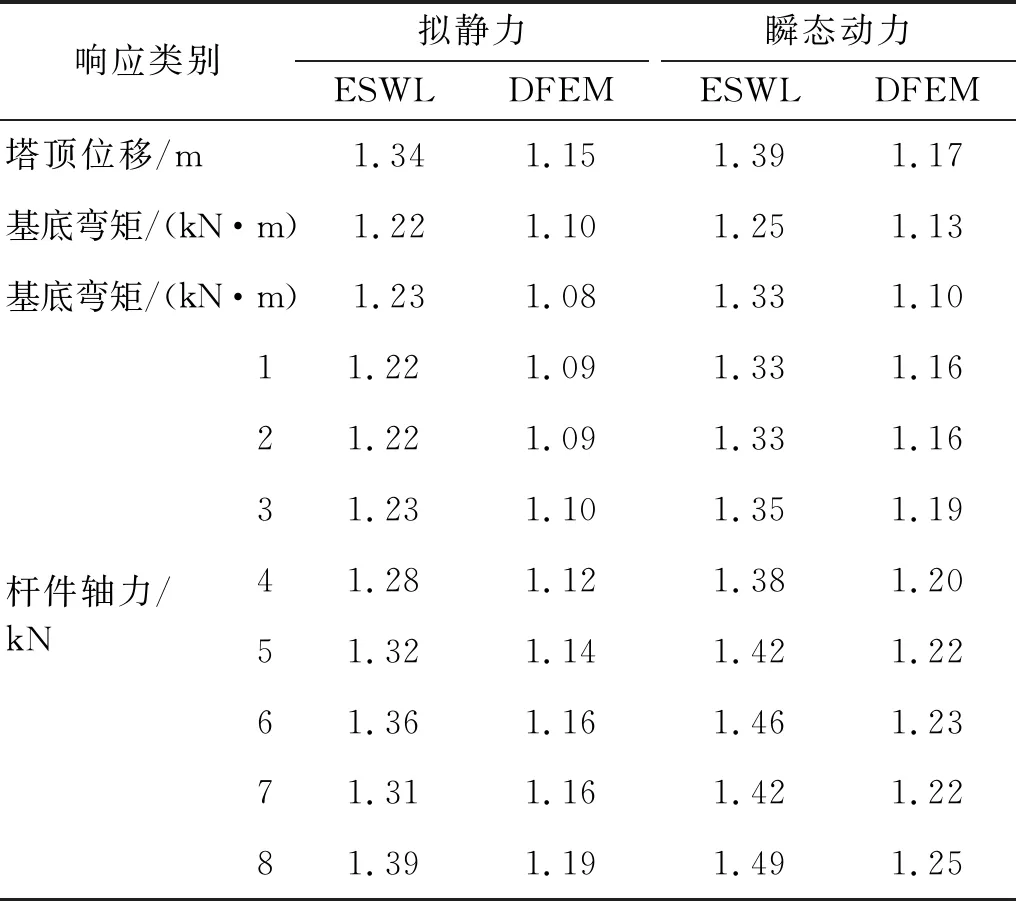
表5 风振系数对比
根据以上时变响应最大值和等效静力风荷载下的结构响应可知,采用上述等效静力风荷载方法计算的结构响应稍偏于保守,即该方法结果具备一定的可靠性,且计算方便,兼顾了工程设计的效率和精度。
5 结 论
本文采用下击暴流风场的平均风和脉动风速的理论模型,模拟了输电杆塔移动冲击风荷载时程。通过对移动下击暴流冲击全过程的静力和瞬态动力有限元分析,结合非平稳随机振动理论方法,考察了移动下击暴流下输电塔风振响应的时域及频域响应特征,最后提出了等效静力风荷载的建议方法。研究得出以下结论:
下击暴流作用下杆塔的平均风静力作用具有显著的时变特征;在冲击全过程中,来流阶段的最大响应接近去流阶段最大响应的3倍;随着来流与杆塔之间径向距离的变化,存在特定的最不利平均风剖面。可将平稳下击暴流的最大风速剖面作为移动下击暴流作用的最不利设计平均风剖面。各类响应下的分析对比表明,该剖面既能包络时变平均风最大效应,又不受响应类型影响,具有良好的适用性。
时频分析表明,下击暴流作用下杆塔的脉动风振响应与平稳良态风振动响应的共性在于两者均以背景分量为主,且共振分量都以一阶模态为主。差异在于前者具有显著的非平稳特性。依据非平稳随机振动的频域计算理论,采用时变均方根的最大值及对应的峰值因子可计算得到冲击过程下杆塔一阶模态响应的极值。
综合上述时变平均风和非平稳脉动风效应的分析及理论推导。采用目前规范的“风振惯性力”法,本文提出了移动下击暴流下输电杆塔的静力等效风荷载的建议公式,且与有限元动力分析结果进行了对比和验证,各类响应时程响应的极值最大偏差在20%以内。表明该方法计算简洁且结果可靠。研究为合理评估输电塔下击暴流设计风荷载提供了有效的探索。
