基于自适应连续小波模极大值算法的车轮擦伤定量评估
2021-06-30施文杰孙宝臣
宋 颖, 施文杰, 孙宝臣
(1.石家庄铁道大学 河北省交通安全与控制重点实验室 交通运输学院,石家庄 050043;2. 西南交通大学 土木工程学院,成都 610031;3. 石家庄铁道大学 大型结构健康诊断与控制研究所,石家庄 050043)
轮对作为连接车辆系统和轨道系统的纽带,对车辆安全平稳运行发挥着重要的作用。但车辆在高速和长距离运行过程中,由于制动不当或雨雪落叶等原因,当制动力大于轮轨摩擦力引起车轮抱死或打滑常常导致车轮踏面形成扁平状区域,即车轮擦伤病害。如哈尔滨检修车间2010年1~5月份共镟修轮对7 899条,其中车轮踏面擦伤的轮对为7 246条,单侧和双侧踏面擦伤轮对分别占擦伤总数的83%和17%[1]。车轮擦伤会产生周期性的瞬态轮轨冲击和振动噪声,对车辆运行平稳性和安全性产生重要影响,特别是对于新形成的踏面擦伤,此时擦伤区域形成脆性很大的马氏体并产生裂纹,如不及时处理任由擦伤发展,裂纹会继续扩展导致马氏体剥落,产生更严重的车轮损伤,引起轮轨接触关系进一步恶化。现场实践表明因车轮擦伤而扣修的车轮大都存在轴承滚珠破裂损坏的现象,这说明从新擦伤发展到旧擦伤的过程中,轮轨之间会产生巨大的冲击力影响,存在着大量的事故隐患[2-3]。因此实时监测车轮擦伤状态并准确评估其损伤程度,把擦伤产生的危害消除在萌芽时期是保证高速动车组安全平稳运行的重要手段。
车轮擦伤动态测量方法包括位移测量法[4]、振动加速度法[5-7]、光电监测法[8]以及超声波无损检测法[9]。现有方法大多为将监测装置安装在轨旁的地面监测方法,与此相对应,轴箱振动加速度法[10]通过在车辆轴箱部位安装加速度传感器,基于轴箱振动加速度特征识别车轮擦伤状态,以其检测实时性、设备安装方便、信号处理算法简单等优势得以广泛应用。由于车轮擦伤引起的轴箱振动加速度信号属于随机振动信号,合理的振动信号时频分析方法是实时准确识别车轮擦伤状态的关键,目前广泛采用的方法主要有短时傅里叶变换、希尔伯特-黄变换、小波变换和魏格纳-威尔分布。其中短时傅里叶变换是在傅里叶变换的基础上对原始信号进行加窗处理,从而具有时频局部化能力。如Brizuela等[11]根据擦伤车轮撞击钢轨产生的单色声波沿钢轨传播过程中的多普勒效应,采用短时傅里叶变换对该信号进行处理,推导车轮擦伤深度和多普勒频率之间的函数关系。该方法只能在车辆低速运行时检测,并且由于窗函数固定计算误差较大。希尔伯特-黄变换是Huang提出的非平稳信号时频分析方法,包括经验模态分解和Hilbert变换两部分。如陈安华等[12]采用该方法对现场实测轴箱振动加速度信号进行处理,通过Hilbert边际谱图识别车轮擦伤产生的特征频率,可有效诊断车轮踏面擦伤,抗干扰能力强,但只能定性识别,无法评估擦伤程度;Li等[13]基于希尔伯特变换提取车辆轴箱振动加速度特征,通过对比正常车轮和擦伤车轮的Hilbert谱,发现擦伤车轮呈现明显的纵向条带状分布,且条带间隔与车速成反比,根据这一特点可识别车轮擦伤病害。小波变换利用可伸缩和平移的小波基函数在时间和尺度上进行信号局部变换,具有频率多尺度特性、时间定位精度高的特点,在车轮擦伤识别领域得到广泛应用。如Ding等[14]采用频率切片小波变换分析轴箱振动加速度仿真信号进行处理,可检测车轮是否存在擦伤;为进一步确定车轮擦伤的位置,廖里程等[15]通过在MATLAB 中设置车轮擦伤外形,采用小波变换系数模极大值实现了车轮擦伤识别与定位;此外,邓文豪等[16]提出改进的自适应形态小波分析方法,可有效提取轴箱振动加速度信号的周期性冲击响应识别车轮擦伤;Jia等[17]提出小波局部能量平均方法和平均信号小波分解方法,通过分析转向架振动加速度信号,可进行车轮擦伤识别与定位。为进一步评估车轮擦伤程度,李奕璠等[18]采用改进的经验模态分解和Hilbert-Huang变换,基于轴箱垂向振动加速度特征在诊断擦伤车轮的基础上,再结合小波包变换识别擦伤程度,该方法不受车速影响,但需要事先建立不同擦伤状态下的小波能量数据库,工作量大且无法定量计算擦伤深度或长度数值。
为了实现高速时车轮擦伤长度的定量评估,本文提出自适应滤波和小波变换模极大值相结合的方法。该方法对高速情形下擦伤车轮引起的轴箱振动加速度信号进行自适应滤波和连续小波变换,通过连续小波变换系数局部模极大值的时间定位特性,推导得出擦伤车轮在钢轨轨面的腾空运行时间与擦伤长度的对应关系,通过动力学仿真实例对识别方法的有效性与影响参数进行研究,从而为定量识别高速动车组车轮踏面擦伤状态提供一种新方法。
1 车轮擦伤状态与轴箱振动加速度理论关系模型
如图1所示,已知车辆的运行速度为v,假设车轮存在长度为L的擦伤,车轮半径为R。根据文献[19],当v小于使车轮腾空的临界速度vcr时,轮对质心的运动轨迹为弧线OCE;当v高于vcr时,车轮脱离钢轨腾空运动,其质心的运动轨迹为弧线ODE,车轮在O点脱离钢轨,在D点再次与钢轨接触。

图1 车轮擦伤计算原理图
车轮离开轨面时,在垂向上有
(1)
式中:M是轮对质量,W是通过轴箱作用在车轮上的质量;g为重力加速度;y是轴心垂向位移。
车轮腾空运动时向心加速度为
(2)
式中,r是弧线OD的曲率半径。
联立式(1)~(2)得
(3)
当r>R时,车轮就会离开轨面;当r=R时,车辆运行速度即为临界速度vcr,考虑轨道柔性及轨下结构对临界速度的影响,引入影响参数γ对临界速度加以修正,即
(4)

vcr=γ(Rμ)1/2
(5)
式中,γ与轨道的几何特性、材料属性和轨下基础的刚度有关,通常取值为2.2。
当v超过vcr之后,车轮腾空做平抛运动,在D点再次与钢轨接触,且接触时刻要早于车轮刚好滚过整个擦伤区域的时刻[20]。设弧OD之间的水平距离为a,根据矢量关系有
(6)
根据式(3)有
(7)
联立式(6)~(7)得
(8)
从而得到车轮腾空时间△t腾和擦伤长度L之间的关系为
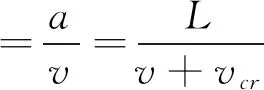
(9)
由于轴箱直接与轮对连接,轮对加速度突变时刻即为轴箱振动加速度突变时刻,设在taxlebox0时刻轮轨脱离接触,此时轮轨垂向力变为零,轮对受力状态发生突变,轴箱加速度随之产生突变;在taxlebox1时刻轮轨重新恢复接触,车轮对钢轨产生冲击力,导致轴箱加速度再次产生突变。因此,擦伤车轮沿钢轨滚动过程中所引起相邻两次轴箱加速度突变的时间间隔记为Δtaxlebox=taxlebox1-taxlebox0。
当轮轨脱离,擦伤车轮在空中做平抛运动时,车轮质心的运动方程OD为
(10)
当车轮擦伤区域与钢轨接触过程中,车轮质心运动方程CDE为
(11)
由文献[21],腾空车轮自taxlebox0时刻与钢轨脱离,在taxlebox1时刻再次与钢轨接触时有y1(x)=y2(x),因此联立式(10)~ (11),得到Δtaxlebox时间内,车轮质心的水平位移△x为
(12)
将式(12)代入式(11),得到Δtaxlebox时间内车轮质心的垂向位移△y为
(13)

(14)
由式(14)可知,通过确定轴箱振动加速度突变时间间隔即可计算车轮擦伤长度。
2 自适应连续小波模极大值原理
车轮踏面擦伤引起的轴箱振动加速度信号,还包含有轨道不平顺和车辆部件振动产生的干扰信号,因此首先对轴箱振动加速度信号进行预处理,采用自适应滤波技术消除干扰信号后再进行连续小波变换,通过提取连续小波变换系数的局部模极大值,确定车轮腾空的起止时刻和运行时间,推导车轮擦伤状态与轴箱振动加速度信号小波变换系数模极大值的关系模型,进行车轮擦伤的状态识别、损伤定位和定量评估。
2.1 自适应滤波技术
利用最小均方误差(least-mean-square,LMS)自适应滤波技术对车轮擦伤引起的轴箱振动加速度信号进行预处理。LMS算法采用瞬时误差能量e2(n)代替均方误差能量E{e2(n)},在每一步迭代中估计出梯度(n),因此只用输入信号X(n)和期望信号d(n)进行迭代,梯度(n)计算公式为
(15)
式中:数据向量X(n)=[x(n),x(n-1),…,x(n-M+1)]T,M为滤波器长度,e(n)是第n次迭代误差,从而得到LMS算法的迭代公式
h(n+1)=h(n)+μ·e(n)·X(n)
(16)
式中,h(n)、h(n+1)分别为第n次和第n+1次迭代得到的自适应滤波器系数。
为保证迭代过程收敛,迭代步长μ必须满足
0<μ<2/MPx
(17)
式中:M是滤波器的长度,PX是信号X(n)的功率。
实际滤波过程中,步长一般为固定值,滤波器长度M和迭代步长μ的选择原则如下[22]:
(1)M不能小于输入信号自相关矩阵非零特征值的个数;
(2)μ取值范围应该满足0<μ<1/MSmax,其最大值μmax通过MATLAB的maxstep函数得到,Smax是信号功率谱密度最大值实际滤波过程中,μ一般取μmax/10。
2.2 小波变换模极大值理论
如果一个平方可积函数ψ(t)∈L2(R)满足容许性条件
(18)
式中:ψ(ω)是ψ(t)的傅里叶变换,则称函数ψ(t)∈L2(R)是一个小波函数。
平方可积函数f(t)∈L2(R)的连续小波变换为
(19)
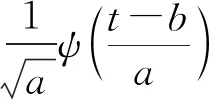
(20)
在某一个尺度a0下,对函数f(t)进行小波变换得到连续小波变换系数Wf(a0,b),如果在b0的某一个邻域内任意点b都满足|Wf(a0,b)|≤|Wf(a0,b0)|,则称点(a0,b0)为模极大值点,|Wf(a0,b0)|为小波变换系数模极大值。
若信号f(t)在t0点附近满足
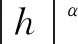
(21)
式中:h是一个大于零的增量,Pn(t)是过f(t0)的n次多项式,A为常数,则称f(t)在t0点的李氏指数为α。
α与f(t)在t0点的可微性有关:f(t)在t0处的导数阶次越高,则α越大,信号在该点处越平滑;若α<1,则f(t)在t0处就是奇异的。Mallat等[23]详细推导了小波变换系数模极大值和信号奇异点的关系,通过小波变换模极大值即可确定信号的突变点。
3 基于自适应连续小波模极大值算法的车轮擦伤识别
3.1 轴箱振动加速度仿真信号的获取
以我国某型高铁动车组车辆和CRTSⅡ型板式无砟轨道为例,通过ANSYS有限元仿真软件和UM (universal mechanism)多体动力学软件联合仿真的方法,采用文献[24]中建立的高速车辆轨道系统刚柔耦合动力学仿真模型,获取车轮踏面擦伤引起的车辆轴箱振动加速度仿真信号。车辆模型中包括1个刚性车体、2个刚性构架、4个柔性轮对和8个轴箱,共15个惯性体,其中车体、构架、轮对各有纵向、横向、垂向、侧滚、点头和摇头6个自由度,每个轴箱有1个点头自由度,整个车辆系统有50个自由度。模型中采用两系悬挂,考虑轮轨接触几何关系非线性、横向止挡非线性、抗蛇行减振器非线性、转臂节点非线性以及空气弹簧非线性特性[25-27],轴箱根据其实际几何参数和材料属性采用刚性轴箱模型。轴箱与轮对之间通过旋转铰连接,考虑点头自由度;采用转臂式定位方式与构架连接,定位节点处通过添加非线性力元模拟橡胶弹性元件的垂向、横向、纵向非线性刚度特性;轴箱和构架之间安装有一系减振弹簧和一系阻尼器。选取轴箱端盖上平面中心点作为轴箱加速度的测量点,获取轴箱振动加速度仿真信号。构架和车体之间通过空气弹簧、二系垂向减振器、二系横向减振器、抗蛇行减振器和横向止挡等元件进行非线性连接,构成车辆模型的二系悬挂系统。轨道结构模型采用UM Flexible Track模块建立,钢轨采用Timoshenko模型,考虑剪切变形,施加我国高速铁路轨道不平顺谱,钢轨与轨下基础采用力元模型连接,模拟弹性弹簧与阻尼。轮轨接触模型采用Kik-Poitrowski轮轨多点非赫兹接触模型。
车轮擦伤模型(图2)表示为滚动圆周不同位置处的车轮半径与擦伤夹角之间的函数关系

图2 车轮擦伤几何形状
(22)
(23)
式中:r(ψ)为擦伤车轮实际半径;d为车轮擦伤深度;L为车轮擦伤长度;R为名义车轮半径;ψ为擦伤区域轮轨接触点与圆心连线和擦伤中心线之间的夹角,变化范围[-β/2,β/2];β为擦伤区域起止点与圆心连线的夹角。
将车轮擦伤模型输入所建立的车辆轨道系统动力学仿真模型,获取高速时不同车轮擦伤长度和擦伤深度引起的轴箱振动加速度仿真信号,为后续基于自适应连续小波变换模极大值识别车轮擦伤提供仿真数据。
3.2 不同擦伤长度识别结果
文献[28]规定,高速动车组车轮踏面擦伤深度不超过0.7 mm,当车辆运行速度为200 km/h时,基于轴箱振动加速度仿真信号对不同工况下的车轮擦伤长度进行识别。具体工况见表1。图3~图5分别为各工况下轴箱振动加速度仿真信号滤波前后时域波形、频谱分布、滤波信号连续小波变换系数以及尺度参数取最优时对应的小波变换系数模极大值。

表1 仿真工况
由图3(a)、图4(a)及图5(a)可知,车轮擦伤引起的轴箱振动响应信号存在明显的周期性冲击,并且轴箱振动加速度峰值随着擦伤深度及长度的增加而随之增大,因此尽早检测擦伤对减少车辆部件关联损伤非常重要。由于轨道不平顺及其它干扰的存在,轴箱振动加速度信号在擦伤区域之外,即坐标轴零轴附近存在明显的波动,对比图3(b)、图4(b)及图5(b)自适应滤波前后的信号可知,振动信号经自适应滤波之后不平顺波动明显减小。此外,由频谱分析可知,采用自适应滤波算法可有效滤除由轨道不平顺产生的低频振动信号,且不同于传统低通滤波器完全滤除信号低频部分,自适应滤波算法在消除轨道不平顺干扰信号的同时保留了车轮擦伤产生的低频振动信息。
图3(c)、图4(c)及图5(c)为采用Daubechies小波(db3)函数对滤波之后的振动信号进行a=1~32连续小波变换结果,可知当车轮存在擦伤时连续小波变换系数出现周期性的亮带,图中越亮的地方代表连续小波变换系数越大,即轴箱振动加速度信号变换越剧烈,相邻两条亮带之间的间隔为车轮旋转一周的时间。
由于擦伤车轮首次脱离和再次接触钢轨时,轴箱振动加速度的变化趋势相反,因此相邻的一对正负小波系数模极大值分别对应车轮脱离和接触钢轨的时刻,其时间间隔为擦伤车轮的腾空运行时间。图3(d)、图4(d)及图5(d)为不同擦伤长度所对应的连续小波变换最优尺度参数取值,即当尺度参数取该值时,根据相邻的一对正负小波变换系数模极大值所对应的时间间隔计算得到的车轮擦伤长度与实际偏差最小。设车辆运行速度为v,轴箱振动加速度信号的采样频率为fs,则相邻两个采样点之间的时间间隔为1/fs。在最优尺度参数取值下,一对正负小波系数模极大值之间的时间间隔可以通过模极大值之间间隔的采样点数得到,进而根据式(14)计算得到车轮擦伤长度
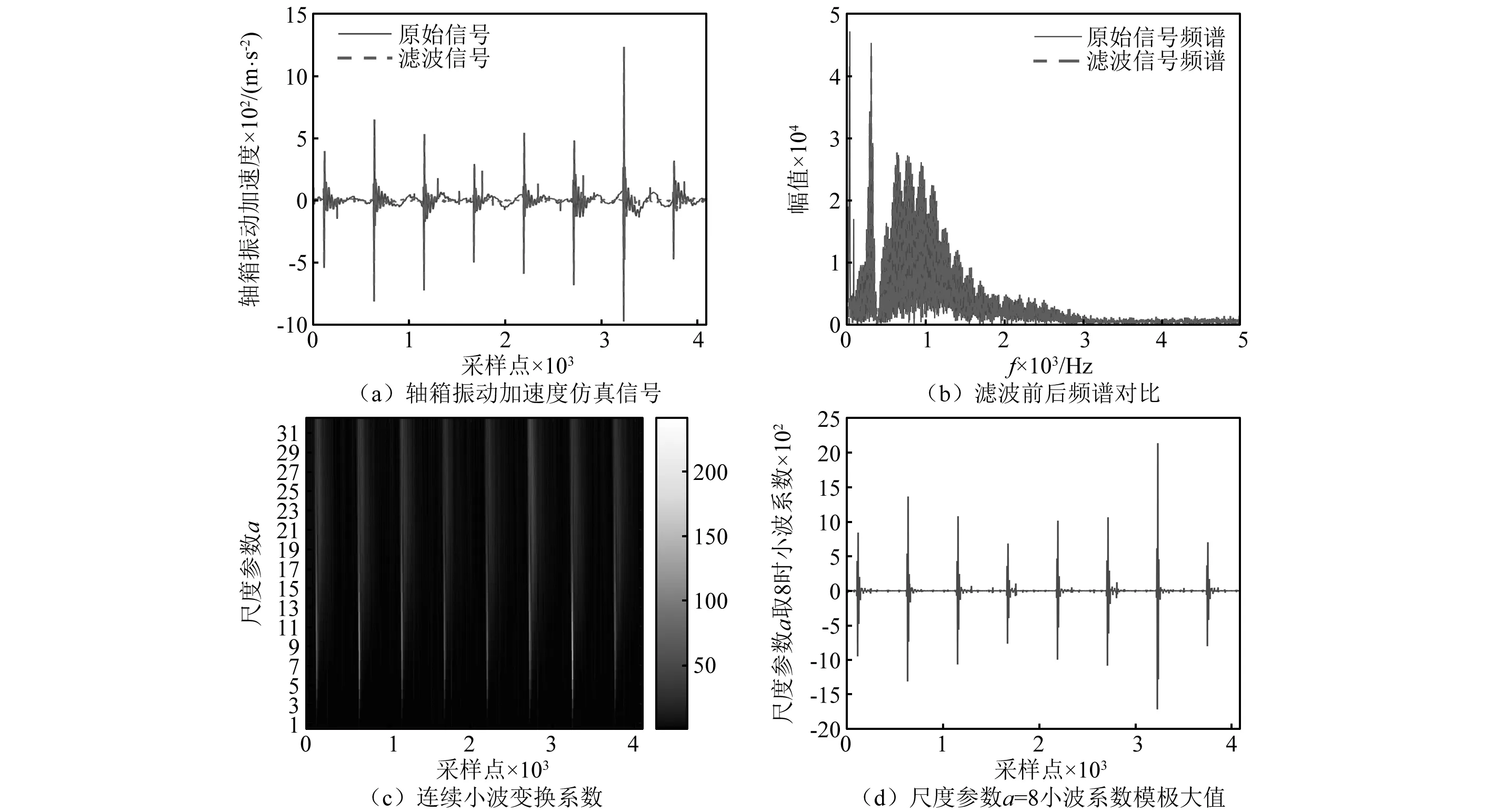
图4 工况2识别结果(v=200 km/h)

图5 工况3识别结果(v=200 km/h)
(24)

对图3(d)中8对正负模极大值之间的采样点数取平均值,得到平均一对正负模极大值间隔的采样点数,即Δ=4.875;由式(5)得vcr=52.8 km/h,将上述参数代入式(24)得L=34.22 mm。由式(23)得理论擦伤长度为33.23 mm,仿真结果与理论值之间的误差为2.98%。工况2、工况3计算过程与工况1相同,不再赘述。

图3 工况1识别结果(v=200 km/h)
3.3 车速对识别结果的影响
为分析车辆运行速度对车轮擦伤长度识别结果的影响,当车辆运行速度为300 km/h时,基于轴箱振动加速度仿真信号对表1三种工况下的车轮擦伤长度进行识别,以便与3.2节识别结果进行对比。图6~图8分别为轴箱振动加速度仿真信号滤波前后时域波形、频谱分布、滤波信号连续小波变换系数以及尺度参数取最优时对应的小波变换系数模极大值。
由图6(a)、图7(a)及图8(a)可知,与车速为200 km/h相比,车辆运行速度越高,轴箱振动加速度信号在擦伤区域之外的波动越剧烈;并且由图6(b)、图7(b)及图8(b)可知,信号能量在低频部分显著增大,即轨道不平顺产生的影响越严重,在车轮擦伤程度较小的情况下甚至会覆盖车轮擦伤产生的振动信号,因此选择合适的滤波方法对轴箱振动加速度信号进行预处理至关重要;此外信号的高频部分能量随着车速增加而随之增大,通过振动信号滤波前后的时域、频域对比发现,自适应滤波算法在车辆高速运行时也具有很好的滤波性能。当车轮擦伤程度相同时,轴箱振动加速度最大值随着车辆运行速度的增加而减小,这是因为车辆运行速度越高,车轮腾空运行时间越短,使得车轮再次与钢轨接触时的动能积蓄随之减小,导致轮轨之间的冲击减小,从而导致轴箱振动加速度最大值随着车速的增加而减小。
由图6(c)、图7(c)及图8(c)可知,随着车辆运行速度的提高,连续小波变换系数中相邻两条亮带之间的间隔随之减小,即车轮擦伤产生的冲击频率与车速成正比。由图6(d)、图7(d)及图8(d)可知,在车轮擦伤长度相同的条件下,尺度参数的最优取值随着车辆运行速度的增加而减小,因为车速增加的同时,擦伤车轮的腾空时间减小,由式(24)可知,此时正负模极大值之间的数据点数Δ必定减小,从而尺度参数的最优取值随之减小。

图6 工况1识别结果(v=300 km/h)

图7 工况2识别结果(v=300 km/h)
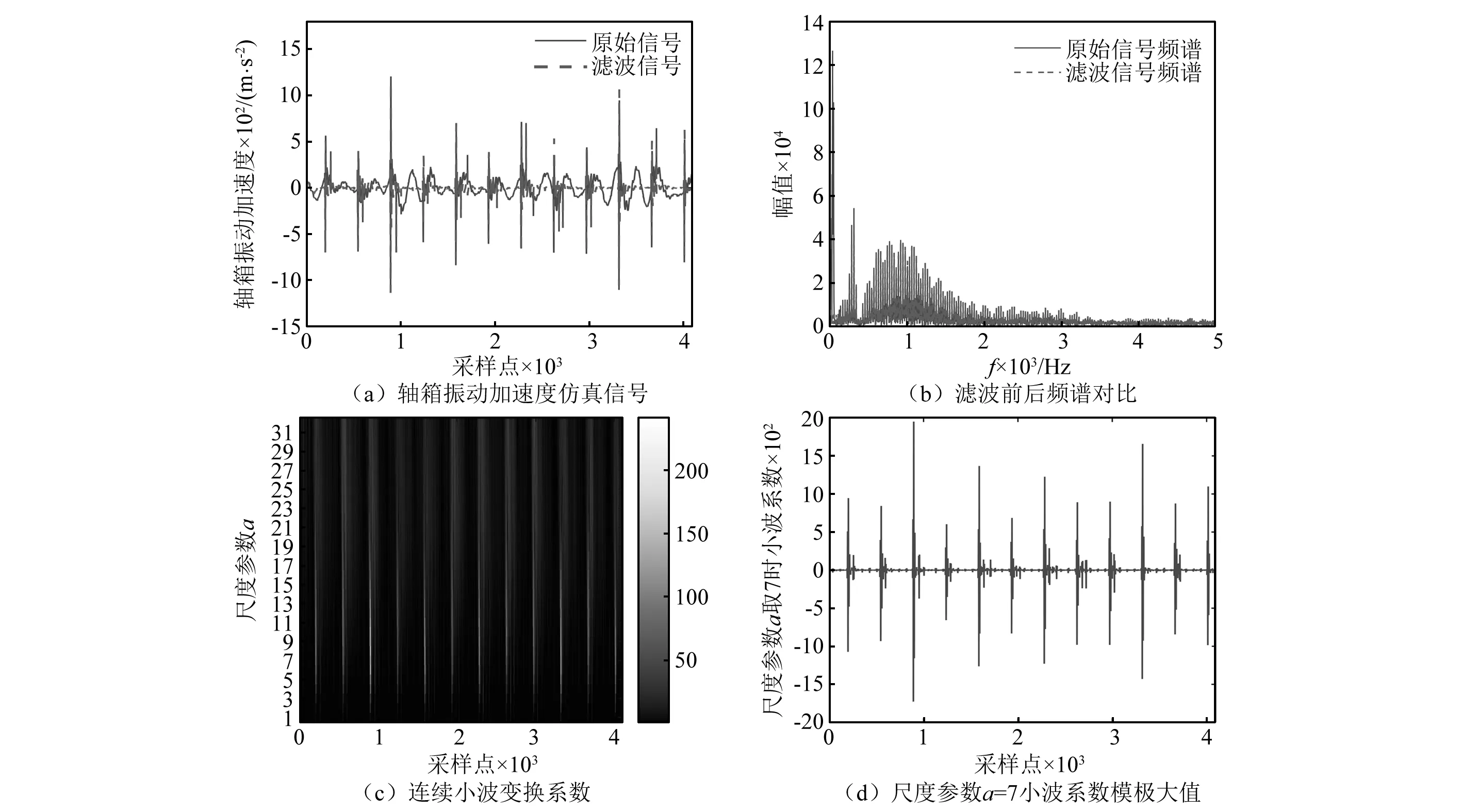
图8 工况3识别结果(v=300 km/h)
3.4 钢轨焊接低接头对识别结果的影响
钢轨焊接低接头等轨面短波不平顺也会引起与车轮擦伤接近的高频问题,两者共存时会对识别结果产生重要影响,因此本文分析了钢轨焊接接头低凹不平顺对不同车速、不同擦伤深度的车轮损伤状态识别结果的影响。其中钢轨焊接接头低凹不平顺采用波长为1 m的余弦波叠加短波不平顺进行模拟[29],仿真工况设置如表2。

表2 仿真工况
其中工况8的仿真分析结果如图9所示。由图9(a)轴箱振动加速度时域响应图可以看出,当车辆运行至钢轨焊接低接头区域时,轴箱振动加速度的响应显著增大,甚至超过了车轮擦伤引起的轴箱振动加速度响应,如图中矩形框所示。由图9(b)轴箱振动加速度频谱可以看出,自适应滤波可以很好的滤除轨道低频干扰信号,但是中高频干扰依旧存在。
由于车轮擦伤引起的脉冲型高频冲击具有周期性特征,因此所对应的相邻两个小波变换系数模极大值的采样点间隔N满足
(26)
式中:v为车辆运行速度,km/h;R为车轮半径,mm;fs为采样频率,Hz。
由图9(c)、(d)连续小波变换系数和小波变换系数模极大值结果可以看出,钢轨焊接低接头并不会影响车轮擦伤作用下小波变换系数模极大值的周期特性。图9(d)中矩形框标出的模极大值突变点即为钢轨焊接低接头引起的,其余以采样点间隔N周期性分布的模极大值为车轮擦伤引起的。因此,基于小波变换系数模极大值的上述周期性变化规律,对于不满足采样点间隔N周期性特征的模极大值予以排除,从而达到准确识别车轮擦伤的目的。
在最优小波尺度参数下,对图9(d)中满足式(25)的每对正负模极大值之间的采样点数取平均值,得到平均一对正负模极大值间隔的采样点数,即Δ=6.167;由式(5)得vcr=52.8 km/h,将上述参数代入式(24)得车轮擦伤长度仿真值L=60.43 mm。由式(23)计算得到理论擦伤长度为60.63 mm,仿真结果与理论值之间的误差为0.32%。

图9 工况8识别结果
综上,当采样频率为10 000 Hz,不同工况下基于自适应连续小波模极大值算法的车轮擦伤长度识别结果与实际长度的误差见表3,最大误差为4.64%,可有效进行车轮擦伤定量识别。相较于文献[30]采用包络谱分析高速车轮擦伤引起的轴箱振动加速度仿真信号特征频率,定性判断车轮是否存在擦伤的方法,通过自适应连续小波模极大值算法评估车轮擦伤长度的方法原理简单,计算误差小,而且可在诊断车轮擦伤的基础上实现擦伤长度的定量评估。

表3 擦伤计算结果
3.5 实测数据验证
采用本文提出的方法对京津城际动车组列车CJ-1车轮轴箱振动加速度实测信号进行分析识别,其中车轮含有显著的13~15阶、19阶、23~25阶多边形,车辆运行速度250 km/h,车轮半径430 mm,加速度传感器采样频率10 000 Hz[31]。识别结果如图10所示。

图10 实测轴箱振动加速度识别结果
由图10(a)可知轴箱振动加速度时域响应信号呈现谐波型波动,与车轮擦伤产生的脉冲型轴箱振动加速度信号显著不同,由此判断轮轨型面存在谐波型短波伤损。由图10(b)、(c)所示轴箱振动加速度连续小波变换系数及其局部放大图可知,连续小波变换系数相邻两个波动峰值之间的采样数据点间隔N1并不是均匀分布,有31点、26点、20点、17点。根据车轮擦伤冲击采样点间隔计算公式(25),在车速为250 km/h,采样频率10 000 Hz的条件下,车轮擦伤引起的轴箱振动加速度连续小波变换系数模极大值采样间隔N2=389。经比较可知,N2≠N1。由此判断车轮踏面没有擦伤病害,应为谐波型伤损,与实测车轮病害类型相符。
4 结 论
本文提出了一种基于轴箱振动加速度信号,联合车辆运行速度和擦伤车轮腾空时间定量评估高速动车组车轮擦伤长度的自适应连续小波模极大值方法,通过仿真实例和与其它文献结果进行对比验证了该方法的有效性。主要结论如下:
(1) 理论推导得出擦伤车轮腾空运行时间与其引起的轴箱振动加速度响应突变时间差相等,因此基于轴箱振动加速度信号自适应连续小波变换结果,采用小波变换模极大值得到轴箱振动加速度突变时间差,再根据车轮腾空时间与车轮擦伤长度之间的理论关系,即可实现车轮擦伤长度的定量评估。
(2) 仿真实例结果表明,自适应连续小波模极大值方法可以有效地识别车轮擦伤长度,与理论计算结果相比,识别误差在5%以内。相较于已有的车轮踏面擦伤定量计算方法,该方法原理更为简便,且能够在车辆高速运行时进行定量评估。
(3) 车轮擦伤引起的轴箱振动加速度连续小波变换系数会出现周期性的亮带,相邻两条亮带之间的间隔即为相邻两次车轮擦伤产生的冲击时间间隔,并且相邻两条亮带之间的间隔随着车辆运行速度的增加而减小,基于该特征可进行车轮擦伤诊断和定位。
(4) 连续小波变换尺度参数a的取值对车轮擦伤识别结果会产生非常重要的影响,因此对轴箱振动加速度信号进行连续小波变换的过程中,应选择合适的方法确定尺度参数a的最优取值。
