一种新型风电塔架结构用双向TMD风致响应减振控制研究
2021-06-30李万润杜永峰
李万润, 杨 州, 杜永峰
(1.兰州理工大学 防震减灾研究所,兰州 730050; 2.兰州理工大学 甘肃省土木工程减震隔震国际科技合作基地,兰州 730050; 3.兰州理工大学 西部土木工程防灾减灾教育部工程研究中心,兰州 730050)
近年来全球环境恶化问题愈来愈严重,使得人们放缓了对传统化石燃料和资源开采的脚步,继而全球各国加快了对可持续再生资源的开发利用工作。根据欧盟委员会的报告,自2004~2015年,风力发电使用率翻了四倍以上,2018年全球风能装机总量超过600 GW,其中仅中国装机容量就达到了221 GW。随着风能市场需求的增长,使得风电单机功率和风轮直径在增长,风轮直径的增长可大大提升单机功率,使得与之匹配的支撑结构塔筒的高度不断增加。华润新能源近日招标公告要求单机功率2.5 MW以上,轮毂高度不低于140 m。随着风机高度的增加,其在动力荷载下的响应面临着越来越严峻的问题。2018年3月2日,山东菏泽某风场中发生风机倒塌事故,事故调查显示,当时风力较大,风机塔筒筒身剧烈晃动,风机主机箱与叶片整体脱落,最终使一个塔筒高为137 m的风机发生倒塌,该次事故主要是由于机舱塔筒顶部振动过大造成结构破坏。如文献[1-2]中所述在外部风荷载作用下,当风速的急速变化时,会引发塔筒产生剧烈的振颤变形,从而引发塔架倒塌;此外,塔筒振动过大会加剧结构的P-△效应,使得下部法兰盘处螺栓损坏,造成底部法兰处疲劳破坏或断裂。风机在额定风速附近正常运行时(风速为10~14 m/s)风机的机舱处常发生偶然性无明显周期的振动,振动过大则会造成风机停机。因此在动力荷载下的大型风电结构频发事故使得大型风电结构动力特性及响应控制亟需研究。在风力发电塔架结构动力分析的研究中,Dragt[3]基于经典随机振动理论完成了风轮随机动力响应分析,并考虑了桨叶气弹效应。余璐庆等[4]考虑了水平刚度和转动刚度之间的耦合,发现了正常运行时风机基础刚度的变化会引发支撑结构的动力特性变化。柯世堂等[5-6]研究了大型风力机塔架式叶片耦合结构风致响应和不同偏航角下风电结构响应,研究表明,大型风力机塔筒-叶片耦合振动呈现出复杂的模态响应和多模态耦合效应,随着偏航角的增大结构响应均值减小但响应方差变大。Huo等[7]基于1.25 MW机组研究了变桨距控制风力机结构的风致响应,考虑了叶片旋转效应、管状塔横风荷载和风向的影响,并对比了数值响应与实测动力响应。Banerje等[8]采用Von karman 谱和Pierson Moskowitz 谱模拟海上随机风荷载和波浪荷载来研究叶片与塔筒耦合效应的影响,研究中建立了一个多自由度体系,将叶片、机舱和轮毂简化为集中在塔顶的质点。Murtag等[9]采用模态叠加法定量计算了三个叶片在风荷载作用时的基底剪力,然后建立塔-机舱-塔筒-叶片耦合,结合运动方程求解耦合作用下塔顶位移,结果表明当叶片与塔筒基频接近时,不考虑耦合作用会大大低估塔顶的响应。在研究和掌握风电结构动力特性的同时,并开展了越来越多的减振控制研究。Stewart 等[10]在机舱内部设置单向TMD装置,以减小海上风电结构在风和海浪荷载下的响应,并可有效提高结构的疲劳寿命。Broderso等[11]通过频域和时域分析研究了ATMD对风电塔振动控制,结果表明ATMD能够明显减小结构的响应。Hemmat等[12]同时使用TLCD和TMD来减小风力发电机基础的振动响应,研究表明TMD装置在风力发电机正常运转下控制效果优于TLCD对结构的控制,而TLCD装置在风电机组处于停机状态下控制效果优于TMD装置。Zuo等[13]使用多个TMD装置控制风电结构振动,结果发现能够有效控制结构的低阶和高阶振动模态,增强了控制效率和控制系统的鲁棒性。Matthe等[14]进行了海上风电结构的被动控制研究,在风电结构机舱内两个正交方向布置两个独立的TMD装置,该方法对结构的响应控制有良好的效果。练继建等[15]针对海上风电结构在极端风荷载下大幅振动问题,采用电涡流-调谐质量阻尼器对其进行减振,结果表明结构的动力响应得到明显减小。戴靠山等[16]将调谐液体阻尼技术与颗粒阻尼技术相结合,提出一种新型调谐液体颗粒阻尼器,并用于风电结构的减振控制。研究结果表明,该方法可有效降低结构的动力响应。陈俊岭等[17]基于TMD原理提出了适用于风电的滚球阻尼器,试验表明该阻尼器在小质量比的情况下可发挥较好的减振功效。章子华等[18]通过在塔筒外部斜拉CFRP索来实现塔筒减振效果,该方法可有效增强结构的侧向刚度,以增大结构的频率,从而实现减振效果。现有研究主要是针对沿风轮主轴方向的振动进行控制,而实际环境中风向与风机轴向夹角达到一定角度偏航系统才进行角度调整,人工维修时偏航系统不能随风向变化和偏航系统故障时风与风机轴向都存在夹角。此时结构振动方向不再沿着风机轴向,单向TMD的控制效率就会降低。因此提出一种双向调谐质量阻尼器(TMD)减振装置,可以控制沿风机轴向的响应,同时也可在风速与风机轴向存在夹角时的结构响应。
1 TMD减振装置
1.1 装置概述及参数确定
本文提出一种双向TMD装置,如图1所示。装置主要由一个质量块和两套弹簧阻尼系统,装置侧壁内侧设置滑轨,在质量块运动时使得两套弹簧阻尼系统顺着滑轨运动,通过质量块上的限位杆,可以将质量块的位移分解为正交的两个位移,弹簧阻尼系统布置在正交方向,避免质量块运动牵连引起刚度阻尼系统的变化,使得双向弹簧阻尼系统的控制参数更精确。质量块底部布置两层相互垂直的滚轴,减小质量块运动时的与底板的摩擦,避免摩擦引起刚度增大。该减振装置实现减振控制的同时,对结构功能影响较小,安装使用面积小,不占据机舱内部空间。将该装置安装在机舱顶部,不会对风场的气流特性产生扰动。

图1 TMD装置图
对风力发电塔安装TMD减振装置,用以控制结构在风荷载作用下的动力响应,本研究中TMD装置的质量取一阶模态质量的3%。其各参数按照文献[19]中最优公式计算TMD的最优频率比和最优阻尼比。
(1)
(2)
式中:μ为TMD惯性质量块质量与结构模态质量比值;fopt为TMD与结构模态的最优频率比;ζopt为TMD的最优阻尼比。
TMD装置的质量、刚度和阻尼的值按式(3)~(5)计算。
md=μm1
(3)
(4)
(5)
TMD装置各参数值,如表1所示。

表1 TMD装置参数表
1.2 减振装置对风电结构控制原理
如图2所示为减振原理图,将风电结构简化为空间双自由度体系(面内与面外均有一个自由度),在引入双向TMD后,整个体系为4个自由度,在整个体系中风荷载仅作用在风机上。M为结构的质量,xM结构的水平位移,C为结构阻尼,K为结构刚度,k为减振装置刚度,m为减振装置质量,c为减振装置阻尼,xd为减振装置位移,P(t)为风荷载,Px(t)与Py(t)分别为风荷载在x与y向的分力。式(6)为风电结构-减振装置系统运动方程:
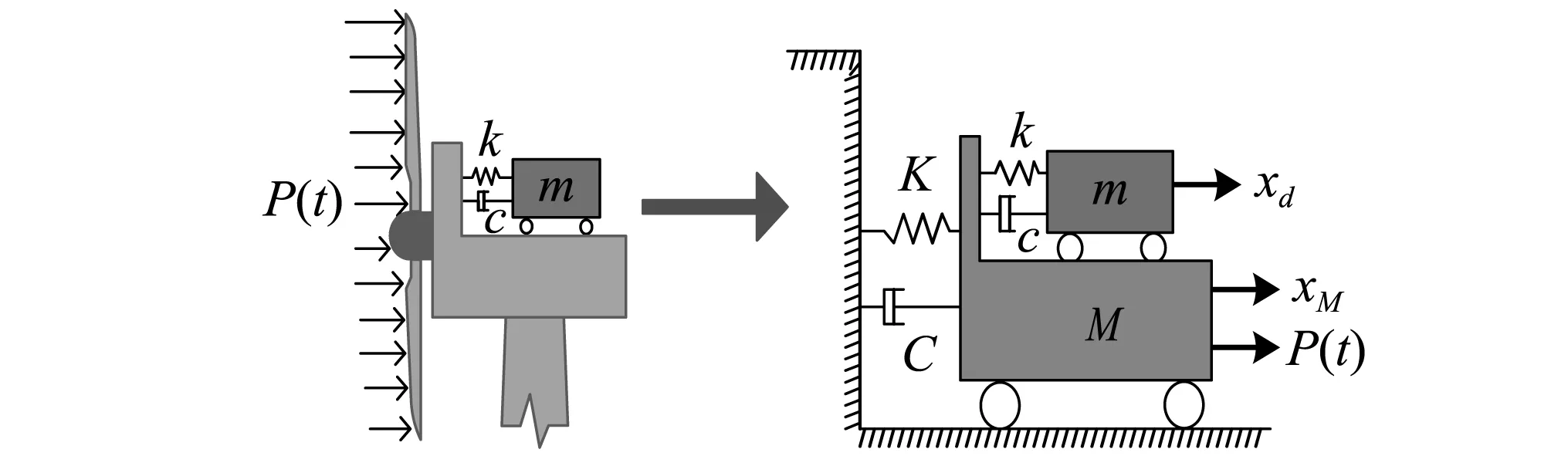
图2 减振原理图
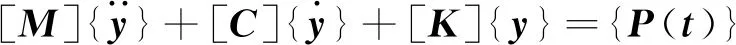
(6)
式中:

2 风电结构模型
2.1 风电结构介绍
选用中国西北地区典型的2.5 MW风电机组为研究对象(如图3所示),该机型塔筒结构高98.12 m,塔筒底部直径为3.9 m,底部筒壁厚67 mm,塔筒顶部直径为2.55 m,顶部筒壁厚20 mm,塔底与塔顶之间截面形式为均匀渐变的形式,机舱高度为3.2 m,重为52 t,桨叶与轮毂质量之和为31.155 t,叶片长为42 m。

图3 风电结构尺寸图
2.2 风电结构有限元模型
建立两种有限元模型:a.考虑叶片、轮毂和机舱的质量的影响,将其简化为一个质点,将其连接在塔筒顶部。将各叶素力累加后施加在塔筒结构顶部质点处;b.考虑包含几何尺寸的叶片与塔筒的耦合,将机舱和轮毂简化为一个质点,叶片采用均质变截面梁,风荷载施加在叶素所对应位置处。两种有限元模型如图4所示。塔筒采用壳单元,网格划分采用扫掠划分,质点采用mass21单元,叶片采用变截面梁单元建立。模型中塔筒和机舱采用Q345钢材属性进行计算,Q345材料屈服强度为345 MPa,材料弹性模量为206 GPa,泊松比为0.3,密度为7 850 kg/m3。叶片采用玻璃钢制成,材料弹性模量为85.5 GPa,泊松比为0.22,密度为1 850 kg/m3。

图4 风电结构有限元模型
2.3 TMD有限元实现
如图2所示,在ANSYS软件中combin14单元为弹簧阻尼单元,其可以同时提供刚度和阻尼。1、2、3和4四个节点为风电结构上的节点,5、6、7和8四个节点分别为装置上与侧壁轨相连的4个点,9号节点用来模拟装置质量块。根据装置特点1、3、5、7具有相同的x位移,因此将1与5,3与7的x方向自由度耦合,5与7节点y方向可自由运动,与装置实物在y方向的滑动一致。同理耦合2与6,4与8的y向自由度,6与8在x方向可自由运动。

图5 装置模型图
2.4 风电结构模态分析
利用ANSYS有限元软件采用PCG Lanczos法进行模态分析。为对比两种模型的频率特性和差异,提取两种风电结构模型的前6阶频率,如图6和图7所示。集中质量模型与叶片-塔筒模型在1~2阶频率较为接近,两种模型均出现了塔筒的一阶弯曲,而叶片-塔筒模型中叶片出现了摆振与挥舞。而3~6阶频率相差较大,集中质量模型表现为塔筒的二阶和三阶弯曲,叶片-塔筒模型中3阶和5阶出现塔筒结构的二阶弯曲,并伴随着叶片的一阶摆振和一阶挥舞,4阶和6阶表现为叶片的一阶异向挥舞和二阶挥舞。风电结构考虑叶片与塔架耦合效应后,各阶模态之间的频率间隔较小,导致两种模型在高阶部分频率相差较大。

图6 集中质量模型前6阶振型图

图7 叶片-塔筒模型前6阶振型图
3 风速模拟及荷载计算
3.1 风速时程模拟
根据中国《建筑结构荷载规范》(GB 50009—2012)[20]采用加拿大Davenport的沿高度不变的脉动风速谱,生成脉动风荷载时程,其计算式为:
(7)
(8)
f=ω/2π
(9)
式中:SV(f)为脉动风速功率谱;k为地面粗糙系数;v10为该地10 m高度处的平均风速;f为脉动风频率;x为湍流积分尺度系数。
分别模拟了额定风速(风力发电机达到额定功率时所对应的风速)和切出风速(风机正常运转时所对应的最大风速)的风速时程,额定风速为11.5 m/s,切出风速为23 m/s,截断频率取8π,地面粗糙度系数取0.002。利用Davenport脉动风功率谱计算塔筒顶部(98.12 m)风速,如图8所示为样本功率谱与目标功率谱的对比,模拟风速计算功率谱与目标谱吻合较好。

图8 模拟风速与功率谱
3.2 风荷载计算
3.2.1 叶素动量理论及叶片荷载计算
叶素动量理论是将叶片沿展向划分为多个微小段,将其上作用力沿长度方向积分得到相应作用力。该研究对象为三叶片水平轴风力发电机,角速度为Ω,弦长为c,升力系数为CL,阻力系数为CD,扭角为β,入流角为φ,攻角为α。如图9所示,v0为风相对叶片的来流速度,a为轴向诱导因子,b为切向诱导因子,ρ为空气密度。
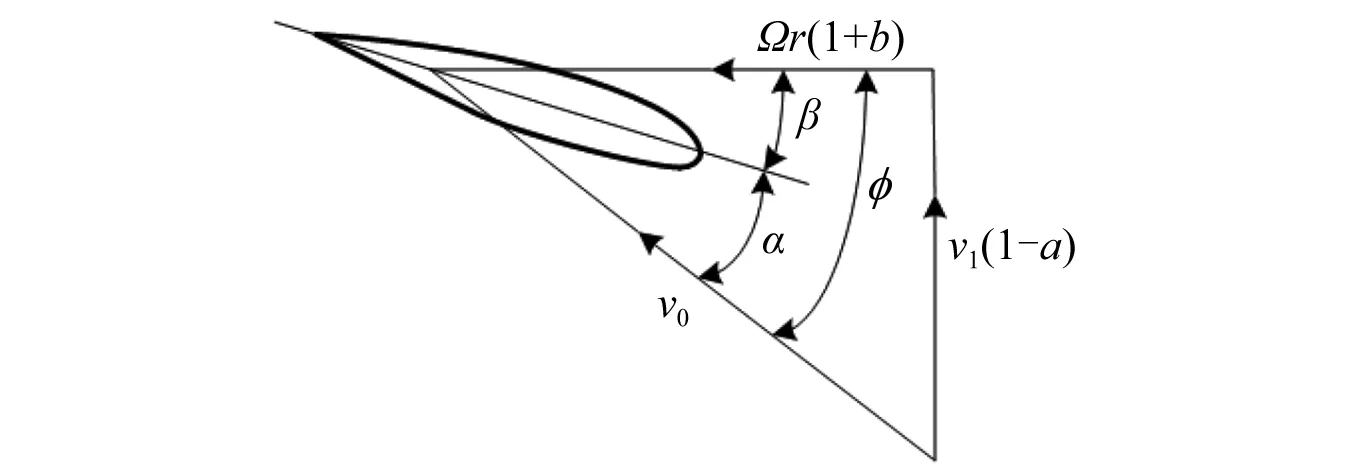
图9 叶素风速度矢量
轴向诱导因子a和切向诱导因子b按式(10)~(11)计算:
a=1/[4 sin2φ/(σCn)+1]
(10)
b=1/[4 sinφcosφ/(σCt)-1]
(11)
式中:Cn=Clcosφ+Cdsinφ,Ct=Clsinφ-Cdcosφ,σ=cB/2πr,B为叶片数目。
考虑叶尖和轮毂处沿展向的二次流作用,引入普朗特损失因子F,即
(12)
式中,rrub为轮毂处半径。
则a和b的表达式为:
a=1/[4Fsin2φ/(σCn)+1]
(13)
b=1/[4Fsinφcosφ/(σCt)-1]
(14)
假设诱导因子的初值,通过迭代求得a,b。轴向诱导因子a大于0.4时的对a需进行Glauert修正,则a的表达式为:
(15)
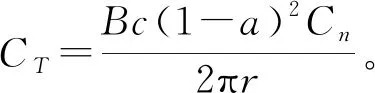
求得诱导因子a和b后,利用下式求得叶素上轴向推力:
(16)
如图10所示为风力发电机三只叶片上轴向总推力图,见图11。

图10 叶素所受作用力示意

图11 叶片总推力
3.2.2 塔筒风荷载计算
风电结构塔筒段选取10个荷载加载点,如图12所示,塔筒上所受荷载的计算根据日本土木学会《风力发电设备塔架结构设计指南及解说》[21]中4.3.5节计算:

图12 塔筒风荷载施加点
(17)
式中:Dt(z)为计算点所在高度处的塔筒直径;DtD为平均风力系数,当计算高度处塔筒外表面处光滑且计算点处风速与塔筒直径之积大于等于6时,CtD取0.6,否则取1;v(z)为计算高度处风速,I1(z)为湍流强度,G为阵风因子,h为计算段塔筒高度。
4 风电结构减振效果分析
以两种不同有限元模型为基础,分别以不同的方式施加风荷载,风电结构的结构阻尼采用Rayleigh阻尼,根据IEC规范[22]风电结构的结构阻尼比取0.01,计算风电结构风致动力响应,并对比两种模型的各动力响应。为对比各响应控制效果,分别以响应的峰值和响应的标准差为控制指标,标准差反应整个时域范围内动力响应的波动特性。
4.1 风电结构位移控制分析
对安装减振装置前后的风电结构响应进行计算,提取集中质量模型塔筒顶部位移和叶片-塔筒模型塔筒顶部位移。未安装减振装置时,集中质量模型塔筒顶部最大位移为0.312 7 m,位移标准差为0.038 4 m,叶片-塔筒模型塔筒顶部最大位移为0.317 5 m,位移标准差为0.036 7 m。安装减振装置后集中质量模型的塔筒顶部位移最大值为0.244 1 m,位移标准差为0.017 7 m;叶片-塔筒模型塔筒顶部位移最大值为0.248 3 m,位移标准差为0.018 1 m。相比于无控时,集中质量模型位移最大值减小21.94%,位移标准差减小53.91%;叶片-塔筒模型塔筒顶部位移最大值减小21.80%,位移标准差减小50.68%。如图13所示为两种模型在无控和安装减振装置后位移时程曲线。

图13 塔筒顶部位移
叶片端部的位移主要由塔筒顶部位移、风机仰角的变化和叶片自身的变形组成。为研究安装减振装置对叶片端部的影响,提取叶片端部的位移,如图14所示为叶片-塔筒模型叶片位移时程图,在未安装减振装置时,叶片最大位移为0.612 7 m,位移标准差为0.068 8 m;在结构安装减振装置后,最大位移为0.479 0 m,位移标准差为0.034 0 m,最大位移减小21.82%,标准差减小50.58%;通过在风电结构机舱顶部安装TMD减振装置减小塔筒顶部位移,进而可减小风荷载作用下叶片的位移。

图14 叶片位移
4.2 风电结构加速度控制分析
通过对装减振装置前后时塔筒顶部加速度响应进行分析。对于集中质量模型,无控时加速度峰值为0.545 2 m/s2,加速度标准差为0.152 1 m/s2,安装减振装置之后其顶部加速度峰值为0.438 5 m/s2,加速度标准差为0.052 6 m/s2;对于叶片-塔筒模型在无控时塔筒顶部加速度峰值为0.537 4 m/s2,加速度标准差为0.142 2 m/s2,安装减振装置后其顶部加速度峰值为0.419 3 m/s2,加速度标准差为0.053 3 m/s2。对集中质量模型安装减振装置之后,顶部加速度峰值减小18.90%,加速度标准差减小65.42%;叶片-塔筒模型在安装减振装置之后,顶部加速度峰值减小21.96%,加速度标准差减小62.51%。

图15 塔筒顶部加速度
为研究安装减振装置后叶片端部加速度的变化,提取叶片-塔筒模型中叶片端部加速度,分析减振装置对叶片动力响应的控制。在无控时叶片-塔筒模型叶片加速度峰值为1.134 8 m/s2,加速度标准差为0.267 3 m/s2, 在安装减振装置之后叶片加速度峰值为0.924 1 m/s2,标准差为0.102 9 m/s2,加速度峰值减小18.56%,加速度标准差减小61.50%。说明可以通过在机舱顶部安装TMD抑制塔筒的加速度来减小叶片的加速度响应。
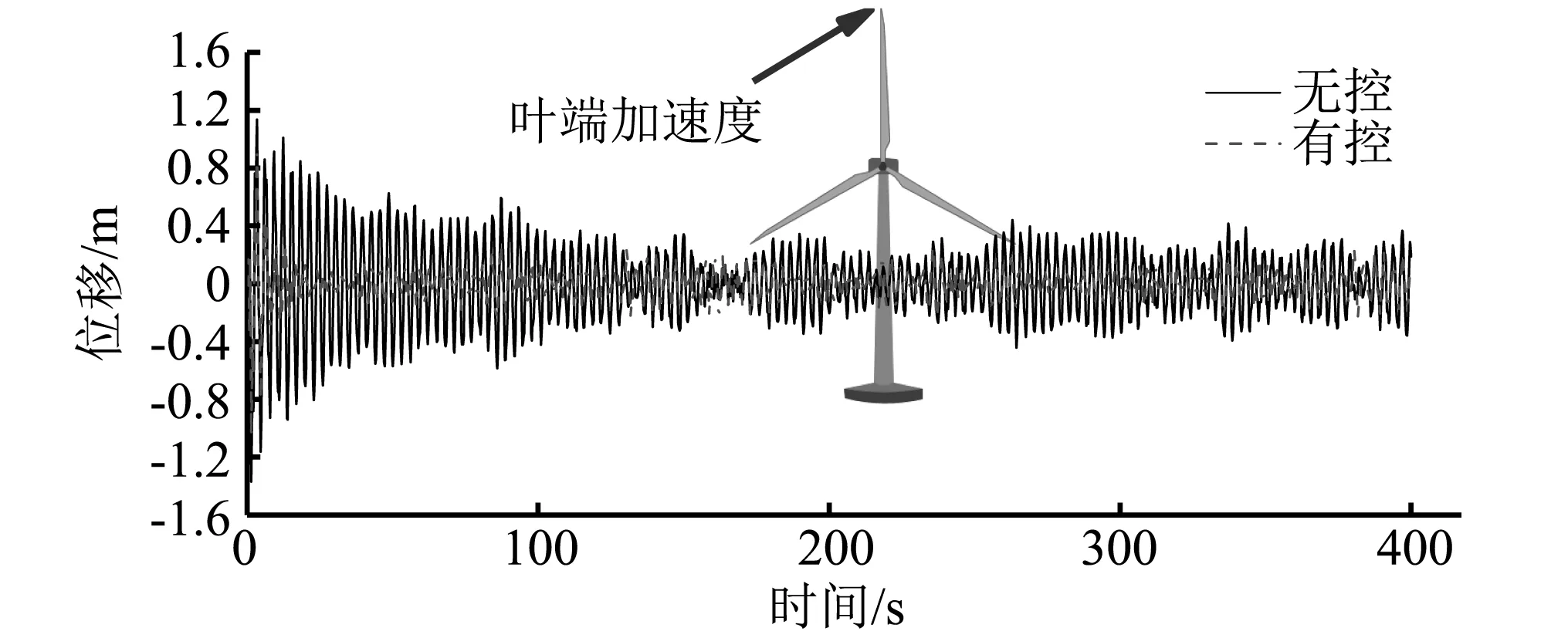
图16 叶片加速度
4.3 风电结构的塔筒弯矩控制分析
对两种模型的塔筒顶部弯矩进行分析,图17为集中质量模型塔筒顶部弯矩图。对于无控时,弯矩峰值为695.145 0 kN·m,弯矩标准差为17.067 3 kN·m;在安装减振装置之后,弯矩峰值为695.470 kN·m,弯矩标准差为7.767 2 kN·m。对于弯矩峰值减振前后未有明显减弱,弯矩峰值出现在0.4 s时,由于TMD具有滞后性,此时TMD减振装置还未进入工作,如图17所示随着荷载的继续作用,在整个时程上,减振装置有良好的减振效果,弯矩标准差减小54.49%。而在现实风场环境中,风荷载会实时作用与结构,因而在真实环境中TMD对响应的峰值减振效果更佳。

图17 集中质量模型塔顶弯矩
图18为叶片-塔筒模型顶部弯矩图,未加控制时塔筒顶部弯矩峰值为810.515 kN·m,加速度标准差为39.054 5 kN·m;在安装减振装置之后,塔筒顶部弯矩峰值813.093 kN·m,弯矩标准差39.085 7 kN·m。在安装减振装置前后,叶片-塔筒模型顶部弯矩响应均未得到明显的减振控制,叶片-塔筒模型顶部弯矩是由叶片上叶素力与力作用点距轮毂中心力矩产生,而集中质量模型等效荷载作用位置为轮毂处,其风荷载作用位置与装置安装位置在同一处,因而在安装减振装置后集中质量模型中塔筒顶部弯矩有明显的减小。

图18 叶片-塔筒模型塔顶弯矩
图19为塔筒底部弯矩,在未安装减振装置时集中质量模型塔筒底部弯矩最大值为18 316.3 kN·m,底部弯矩标准差为2 291.989 8 kN·m;安装减振装置之后塔筒底部弯矩最大值为17 843.7 kN·m,弯矩标准差为1 080.100 3 kN·m,弯矩峰值减小2.58%,弯矩标准差减小52.88%。对于叶片-塔筒底部弯矩,在未安装减振装置时叶片-塔筒模型塔筒底部弯矩最大值为18 177.2 kN·m,弯矩标准差为2 168.235 6 kN·m;安装减振装置之后风电结构塔筒底部的弯矩最大值为17 710.8 kN·m,风电结构塔筒底部弯矩标准差为1 095.597 2 kN·m,弯矩峰值减小2.56%,弯矩标准差减小49.47%。弯矩峰值控制率较小主要是由于弯矩峰值出现在风荷载刚作用于结构时,减振装置还未发挥减振功能。

图19 塔筒底部弯矩
4.4 两种风电结构模型响应对比
对两种不同模型的风电结构进行时程分析,分别对比集中质量模型和叶片-塔筒模型在安装减振装置前后各响应的峰值和标准差,从表2可以看出两种不同模型在未控时的塔筒顶部位移、塔筒顶部加速度和塔筒底部弯矩的峰值和标准差计算结果相差基本在5%以内,而两种模型塔筒顶部弯矩的峰值和标准差计算结果相差较大,峰值相差16.60%,表明在风荷载下的塔筒顶部弯矩相差较大;标准差相差128.89%,表明脉动风下顶部弯矩响应相差较大。主要是由于叶片-塔筒模型叶片上叶素力作用点与轮毂间的偏心存在,使得其相对于集中质量模型的塔筒顶部弯矩较大。

表2 两种模型减振前后响应对比
在安装减振装置之后,集中质量模型与叶片-塔筒模型的塔顶位移、塔顶加速度和塔底弯矩均有减小,而塔筒顶部弯矩的控制两种模型出现较大差异,集中质量模型塔筒顶部弯矩的峰值减小效果不明显,而弯矩标准差的控制效果较好,叶片-塔筒模型顶部弯矩峰值和标准差均未减小。
4.5 切出风速下风电结构模型响应
表3为在切出风速下,风电结构的各响应和减振控制效果。从表3看出两种风电结构有限元模型在除塔筒顶部弯矩差异较大外,其他各响应都比较接近,与结构在额定风速下的规律基本一致。在位移和加速度两个响应控制中效果较为明显,与之前额定风速下控制效果一致;塔筒顶部弯矩的控制效果依旧相差较大,对集中质量模型的塔筒顶部弯矩控制效果较好;在切出风速下对塔筒底部弯矩峰值的控制效果较额定风速下明显,集中质量模型的塔底弯矩峰值减小9.86%,叶片-塔筒模型底部弯矩峰值减小10.02%。

表3 两种模型减振前后响应对比
4.6 不同夹角下风电结构响应控制
风机在正常运转时,风速矢量的方向变化超过一定角度时偏航系统才可调整风机对准风机,人工检修时偏航系统处于关闭状态、偏航系统出现故障时和90°侧风时,这些状况下不能使风机处于迎风状态。图20为风速矢量与风机轴向间夹角δ。为分析在不同夹角下双向TMD对结构的控制效果,选取δ为30°、45°和60°三种工况,分别分析各工况下风电结构的顶部位移、加速度和塔筒底部弯矩的减振控制效率,计算中忽略了风速夹角对叶片旋转速度的影响。

图20 风与风电结构夹角
图21为安装TMD装置前后两种模型在不同夹角时响应峰值和响应标准差的减小率。从图中可知,在不同夹角下减振装置对顶部位移和加速度响应峰值控制效果明显,对两种模型塔底弯矩的峰值控制效果较弱。两种模型响应的标准差控制效果明显。随着角度的变化,峰值和标准差的减小率存在差异,但在夹角变化时未出现较大差异,说明减振装置在不同风夹角下均能发挥良好的减振功能。
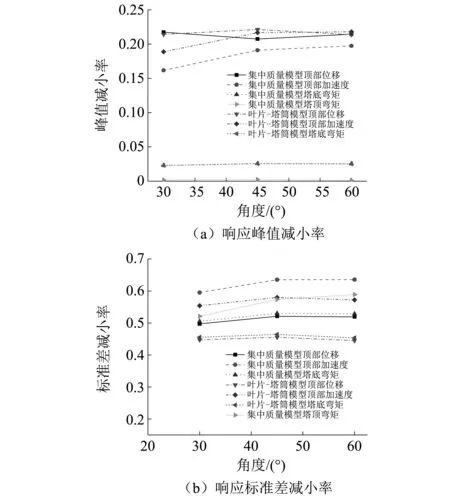
图21 不同夹角下风电结构响应减小率
分析结构在额定风速下的响应控制后,针对切出风以不同角度作用下的结构的控制效率进行计算分析。图22为风电结构在切出风速时风电结构在安装TMD前后的响应的峰值和标准差减小率对比。在不同风夹角时,两种模型顶部位移和顶部加速度的峰值控制效果明显,对塔顶弯矩峰值控制依旧较弱。在对响应标准差的控制中,各响应的减小效果均比较明显,在不同角度时,各标准差减小率虽有变化,但总体的控制效果明显。在切出风速下,风电结构各响应的峰值减小率较切出风速时有所提高,各响应的标准差的控制率也有所提高。

图22 不同夹角下风电结构响应减小率
5 结 论
本文提出一种新型用于风电塔架结构减振控制的双向TMD装置,并采用两种模型对其减振效果进行了分析,得到以下结论:
(1)通过在机舱顶部安装减振装置后,不仅有效减小塔筒的顶部位移、顶部加速度和塔筒底部弯矩,还可有效减小叶片的位移和加速度。
(2)在风荷载作用下,两种不同模型的塔筒顶部位移、加速度和塔筒底部弯矩计算结果一致,而塔筒顶部弯矩在不同模型中相差较大,叶片-塔筒耦合模型顶部弯矩计算结果大于集中质量模型,通过对比两种模型响应差异,为分析不同响应对象时模型的综合选取提供参考依据。
(3)与额定风作用结构时相比,切出风速下TMD对风电结构的各动力响应的减小率有所增加,表明了在切出风速下TMD的控制效率有所提升。
(4)在风速与风电结构的夹角变化时,该双向TMD对结构的控制仍有良好的控制效果,说明夹角对TMD的控制效率影响较小。
