轴力和水压作用下深水输液管道湿模态振动特性分析

余建星， 李振眠， 余 杨， 赵明仁， 崔宇朋， 赵 宇， 徐立新

(1. 天津大学 天津大学水利工程仿真与安全国家重点实验室，天津 300350；2. 天津大学 天津市港口与海洋工程重点实验室，天津 300350)

深水输液管道是海洋油气资源开发的“生命线”，在复杂外界激励作用下会发生振动变形，影响正常工作，甚至产生结构破坏和石油泄漏等灾难性后果。据统计，在全球化工行业发生的重大事故中，管道振动引起的比重高达19%[1]。因此，开展深水输液管道振动特性分析具有非常重要的现实意义。对于深水输液管道，其组成包括管道、内部原油和外部海水，内外流场的存在会对管道振动特性产生影响。另外，生产立管和深水管道系统等的设计要考虑外部水压和轴向拉力的联合作用[2-3]。以张紧式、悬链式立管为典型的生产立管总是处于两端受拉的状态[4]。海底管道在服役和检修阶段，管道发生的轴向位移和横向位移会导致轴向拉伸力增大[5]，从而使管道承受轴拉和水压联合作用。所以，开展轴力和水压作用下深水输液管道湿模态振动特性分析，具有实际工程应用价值。

国内外学者已对充液管道振动问题开展了大量的研究[6]。1950年Ashley等[7]首次提出了输液管道流固耦合的概念，对输液管道的横向振动进行了研究。Dai等[8]采用传递矩阵法研究了流体流动引起的组合力对输流直管和弯管固有频率的影响。Zhang[9]运用波传播方法将流体处理为理想声介质，研究了圆柱形输液管道的振动特性。Liu等[10]运用波传播方法研究了简支埋地管道的振动特性，发现周围介质刚度会显著影响管道的固有频率。杨超和范士娟采用特征线法研究了管道的流固耦合振动问题，证明了该方法的正确性和有效性。Huang等[11]采用消元Galerkin方法计算不同边界条件下直管固有频率，得到了不同边界条件的输流管道的固有频率方程。Zhu等[12]提出了一种基于谱元法的管道振动特性分析方法，并说明该方法在复杂输流管道的振动建模中的应用潜力。姜峰等[13-14]应用ANSYS的Acoustic Extension插件开展具有内外流场的管道振动特性分析。

由于管道长径比较大，管道振动研究时往往采用梁振动理论。但是管道作为薄壁壳结构，其振动不仅有长度方向上的梁振动模态，还有圆截面上的板壳振动模态[15]。管道的板壳振动存在多种模态形式，会造成圆柱截面变形，从而使截面承载能力下降。为更准确地反映输液管道的实际物理系统，输液管道可以处理为圆柱壳模型，因此圆柱壳体振动研究可为管道振动问题提供参考。Junger[16]的研究表明外部流体对结构振动特性的影响可以等效为附加质量和阻尼力，且会导致结构频率大幅减小。Fuller[17]假设流体为可压缩的理想声介质，应用波传播方法分析了流场中圆柱壳的频散特征。Zhang等[18]将壳体位移以波传播的形式进行级数展开，通过正交化振动方程得到了特定模态下的频散方程。王鹏等[19]考虑自由液面、刚性底面和组合边界等的影响，用波传播法和虚源法分析了声边界约束下水中有限长圆柱壳的声振特性。Liu等[20]以预应力的形式考虑了壳体的流体静压，采用波传播方法分析了流体静压对浸没圆柱壳频散特性的影响。Zhu等[21]考虑轴向和横向的静水压力，建立了浸没圆柱壳的流固耦合频散方程。Ergün等[22]假定内部流体黏性不可压缩，研究了具有初始应力的圆柱形粘弹性厚管中的谐波问题。

目前管道流固耦合的研究主要集中在内外流场的耦合作用，对管道设计中重要的轴向拉力和外部水压的联合作用问题较少涉及。本文基于波传播法，采用采用Love-Timoshenko理论和Helmholtz方程建立耦合系统模型，聚焦于轴力和水压作用下深水输液管道湿模态壳振动特性研究，旨在为深水输液管道结构设计和优化提供参考依据。

1 研究对象

本文以轴力和水压作用下深水输液管道为研究对象。如图1所示，管道长度为L，壁厚为h，中性面半径为R，材料密度为ρs，杨氏模量为E，泊松比为μ。管道外部为海水组成的静止流场，静水压力为p0，海水密度为ρe，声传播速度为Ce。管道内部为流动速度为Vi的原油，原油密度为ρi，声传播速度为Ci。以x，θ和r分别表示管道的轴向、周向和径向，u，v和w分别表示管道中面轴向、周向和径向位移。管道受到外部静水压力为p0，两端面受到轴向拉力为Ta。

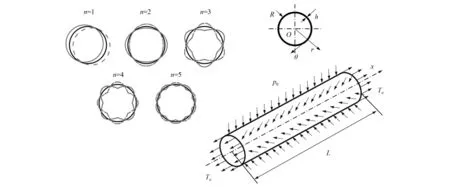
图1 深水输液管道结构及其周向模态振型示意图

2 基本理论推导

2.1 壳体动力平衡方程

根据Love-Timoshenko壳体理论[23]，管道动力平衡方程表达为

(1)

式中：Pf为原油和海水产生的流体声压； [L]为3×3的矩阵，各元素如下：

根据无矩理论可得单位长度的轴向力和环向力分别为

(2)

(3)

2.2 内外流场的模拟

采用波传播方法，将壳体位移在轴向和周向展开成双Fourier级数形式

(4)

式中，kmn为轴向波数，根据壳体两端边界条件确定。

假设海水和原油均是无黏、各向同性且无旋的，则可处理为理想声介质，用具有轴向均匀流动的声学波动方程方程[24]描述

(5)

式中：M为流体马赫数；cf为流体中的自由波数。

考虑Sommerfeld辐射条件以及Neumanu边界条件，采用分离变量法可得满足方程式(5)的流体声压场的解

(6)

在流体和壳体的接触面上，二者径向位移相等

(7)

将式(4)和(6)代入式(7)，正交化处理后得到

(8)

2.3 耦合动力方程

将式(4)、(6)和(8)代入式(1)，进行正交化处理后化简可得耦合动力方程

[S][UmnVmnWmn]T=[0 0 0]T

(9)

式中， [S]为3×3的矩阵，各元素如下：

(10)

(11)

方程式(9)必有非零解，则其系数矩阵满足|S|=0。当给定轴向波数kmn时，|S|=0仅包含变量无量纲频率Ω，采用可求解超越方程的改进牛顿迭代法[25]即可获得深水输液管道的固有频率。

3 方法验证与管道参数

3.1 准确性验证

为验证本文方法的正确性和程序的可靠性，对文献[26-28]中的模型进行计算并对比结果。验证模型的参数为：钢壳体，弹性模量2.1×1011N/m2，泊松比0.3，壳体密度7 850 kg/m3，厚度0.01 m，半径1.0 m，壳长20 m。流体声速1 500 m/s，流体密度1 000 kg/m3，外部水压40 kPa。计算结果对比如表1所示，显然本文计算结果与文献结果吻合程度非常高。因此，本文的理论模型和计算程序是准确可信的。

表1 不同状态下圆柱壳固有频率验证

3.2 计算模型参数

计算模型选用材质Q235B的深水管道，涉及四种工况，分别是真空中空管道、真空中充液管道、水中空管道、水中充液管道和轴力-水压联合作用下水中充液管道，依次记为P1、P2、P3、P4和P5。以P5为例，主要参数如表2所示，边界条件为两端刚性固定(C-C)。

表2 深水管道-流场耦合模型参数

4 结果分析与讨论

4.1 管道-流场耦合系统参数分析

首先开展管道-流场耦合系统参数分析，计算了两端刚性固定(C-C)和两端简单支撑(S-S)两种不同边界条件下不同长径比(10-60)P5工况中管道的无量纲固有频率。采用梁函数近似模拟壳体边界：对于C-C，kmnL=(2m+1)π/2；对于S-S，kmnL=mπ。对于管道结构，m=1时的固有频率较小，n取小值时就足以反映结构的振动特性。因此，仅给出m=1，n=1,2,…,5时的无量纲固有频率值，如图2所示。

图2 C-C和S-S下不同L/R管道无量纲固有频率(m=1)

由图2(a)可知，对于C-C边界条件，不同长径比管道高周向模态固有频率随着n增大而增大，但低周向模态固有频率有所差别。对于L/R=10，n=1时无法获得管道模态频率，即出现模态截断。此时，n=2为最小固有频率，即基频。对于L/R=20，n=1的频率高于n=2的频率。此时，频率随着n先减后增。对于更大的长径比，基频出现在n=2时。另外，随着周向模态数的增大，不同长径比对应的固有频率趋于一致。由此可见，长径比对管道的低周向模态固有频率影响较大，对高周向模态固有频率影响较小。对于较小的长径比，基频在(m=1，n=2)模态；对于较大的长径比，基频在(m=1，n=1)模态。

图2(b)为S-S边界条件下管道的频率折线图。可以看出，该频率折线与C-C边界条件的折线变化规律大同小异。不同的是：对于L/R=10，n=1没有出现模态截断，但基频依然出现在n=2；对于L/R=20，基频出现在n=1。比较图2(a)和图2(b)相同长径比、相同模态的频率值，发现对于低周向模态固有频率，S-S情况总小于C-C情况，而随着周向模态数的增大，二者差异减小。对于较大的长径比，不同边界条件的高周向模态固有频率甚至相等。由此可见，边界条件对管道的低周向模态固有频率影响较大，对高周向模态固有频率影响较小。

4.2 内外流场影响分析

计算了P1-P5五种工况的无量纲固有频率，结果如图3所示。从图3可以看出，每个工况的固有频率随着周向模态先减后增，基频出现在n=2。可见，海水和石油的存在不会改变管道固有频率的变化趋势，轴力和水压的作用亦是如此。对于相同的n，频率大小关系为P1>P2>P3>P4。可见，海水和原油对管道固有频率有影响，内外流体的存在将降低管道的每一阶模态的频率。另外，P4>P5表明轴力和水压的作用会降低管道的固有频率。详细地，以P1工况为参考，计算了其他工况基频相对变化率，如表3所示。

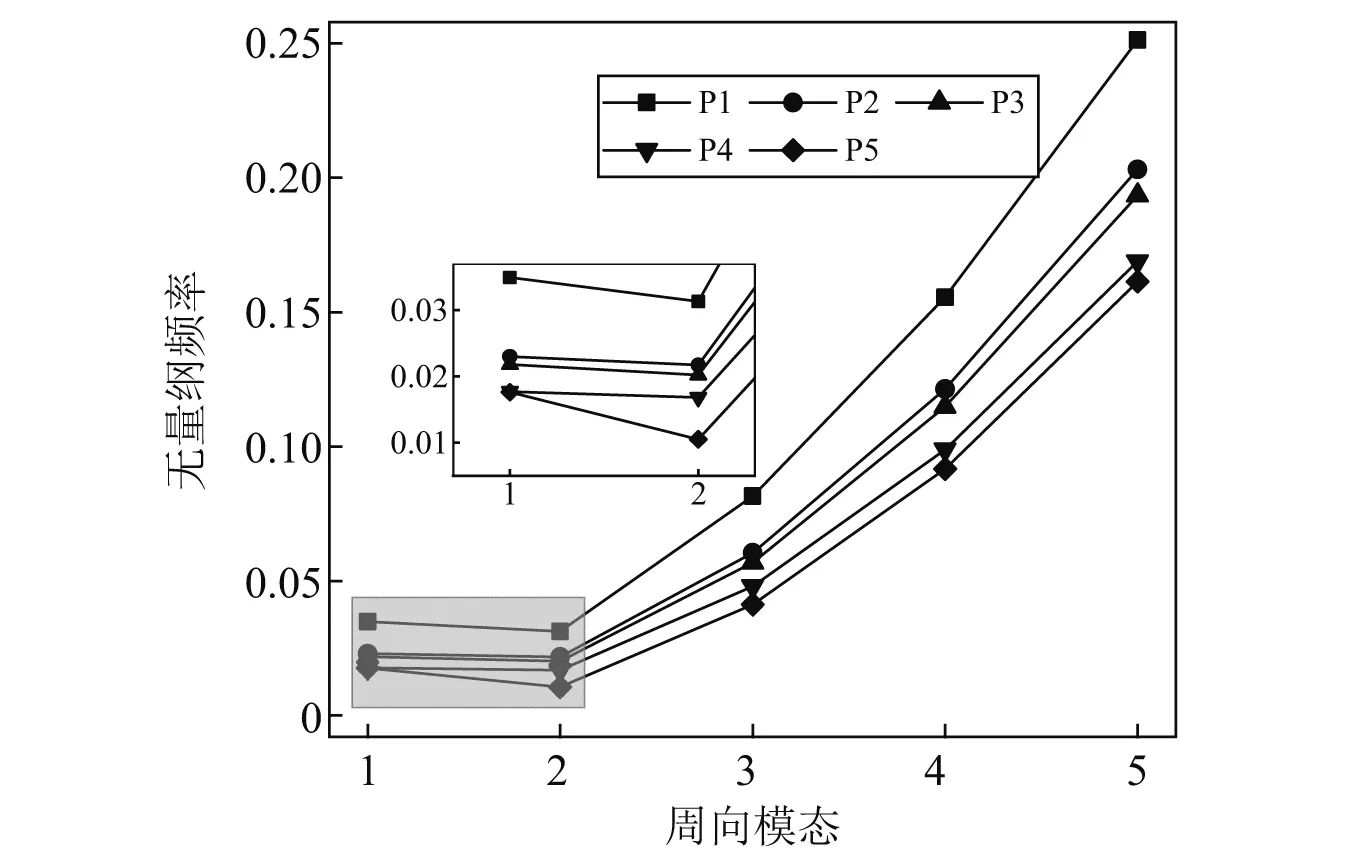
图3 不同工况中不同周向模态的管道无量纲固有频率(m=1)

表3 不同工况管道最低频率相对变化率

从表3可以看出，原油-管道耦合的基频降低了30.67%，海水-管道耦合的基频降低了35.46%，石油-管道-海水耦合的基频降低了46.33%。可见原油对管道最低固有频率影响小于海水，两者同时作用时的影响小于各自影响的简单叠加。P5反映了轴力、水压、原油和海水同时存在时管道基频下降了66.45%。同P4对比，可见轴力和水压作用对深水输液管道最小固有频率影响不可忽视，更多的讨论在4.3节。

为研究管内原油流速对管道固有频率的影响，计算了不同马赫数下P5管道的固有频率。参考文献[9]，定义原油流速与振动波传播方向相同时固有频率为下流频率fd(M>0)，反之为上流频率fu(M<0)。那么，管道真实固有频率为fm=2fdfu/(fd+fu)。以P5为参考，不同|M|值管道不同周向模态的无量纲上流频率和下流频率相对变化率如图4所示。由图4可知，管道下流频率随着原油流速的增大而增大，上流频率随着原油流速的增大而减小。对于相同的马赫数，基础固有频率(n=2)变化幅值最大，而其他周向模态的变化率则与周向模态数正相关。可见，当原油流速与振动波传播方向相反时，管道结构稳定性随着流速增大而小幅下降。因此，应重点关注管道振动波传播的上流区域。

图4 不同马赫数下管道上下流频率变化率

利用图4的结果计算管道真实固有频率，其中最重要的基频变化率如表4所示。由表4可见，原油流速对管道真实基频的影响在1%之内。因此，分析深水输液管道振动特性时忽略原油流速影响不会引起太大误差。

表4 不同马赫数管道基础固有频率相对变化率

4.3 轴力和外水压影响分析

从4.2节的分析中初步可以看出，轴向拉力和外水压的联合作用会降低深水输液管道的各阶模态固有频率。图5的(a)和(b)分别给出了P5管道在不同轴向拉力和不同外水压下固有频率的变化情况。变化率的参考值为表2对应的管道。

(12)

从图5(b)可以看出，外水压对管道各个模态的固有频率影响较大。随着外水压的增大，频率减小，但各个模态变化幅度大小不一，基本与周向模态数呈正相关。特别地，n=2时频率变化幅度最大，而且随外水压的增大而急剧减小。如果继续增大外水压，n=2时固有频率将出现负值，意味着管道刚度丧失，结构失稳。进一步地，计算频率为零时外水压，即管道临界压力的弹性理论解。

图5 轴向拉力和外部水压对管道固有频率的影响

采用文献[21，30]的方法，计算P5和P1、P2、P3和P4四个工况的管道在外压作用下基频，并绘制基频的平方与外水压的关系图，如图6所示。从图6可以看出，基频的平方与外水压近似呈线性关系。这与文献[21，30]的结论一致。另外可以看出，各个直线的斜率不等，大小关系为P1

对图6所示的五条直线进行拟合，求出直线与横轴的交点，得到临界压力值如表5所示。比较P1、P2、P3和P4的临界压力，变化幅度小于0.2%，可以认为内外流场对管道失稳的临界压力不会产生影响。比较P4和P5的临界压力，可以发现轴力的存在将降低管道的临界压力值2.44%。这与文献[3-5]发现的规律一致。

图6 无量纲基础频率平方值vs外部水压

表5 不同工况管道失稳临界压力值

另外，采用有限元方法开展无轴力和有轴力时管道的特征值屈曲分析，得到临界压力值分别为3.494 9 MPa和3.423 1 MPa，与本文计算结果相差1.51%和1.91%。本文方法与有限元方法计算结果十分接近，进一步说明了本文方法的正确性。由此可见，管道轴向受力对管道的临界压力存在一定影响，在管道失稳分析中轴向力不可忽略。

5 结 论

本文采用Love-Timoshenko理论和Helmholtz方程建立了轴力和水压作用下原油-管道-海水耦合模型，计算得到了深水输液管道壳振动周向模态的固有频率，并研究了边界条件、长径比、内外流场耦合以及轴向拉力、外部水压对管道固有频率的影响，得到以下结论：

(1) 边界条件和长径比对深水输液管道的高周向模态固有频率影响较小，但对低周向模态固有频率影响较大，特别是基频。对于低周向模态固有频率，两端简支情况总小于两端刚性固定情况，而随着周向模态数的增大，两种边界条件的固有频率差异减小，最终相等。对于较小的长径比，管道基频在(m=1，n=2)模态；对于较大的长径比，管道基频在(m=1，n=1)模态。

(2) 原油、海水的存在会明显地降低管道固有频率。原油对管道基频影响小于海水，两者同时作用时的影响小于各自影响的简单叠加。原油和海水的存在对管道失稳的临界压力不会产生影响。管道上流频率随着原油流速的增大而增大，下流频率随着原油流速的增大而减小，而原油流速对管道真实频率的影响可以忽略不计。因此，对于深水输液管道的振动分析，湿模态分析具有不可替代性。

(3) 轴向拉力会小幅降低管道基频，进而小幅降低管道失稳临界压力。水压会大幅降低管道基频，甚至引发结构失稳。因此，在深水输液管道湿模态分析和失稳分析中轴力和水压作用不可忽略，特别是对水压作用应加以重视。