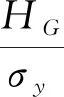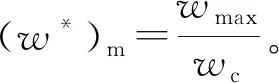恒定外力作用下的碰撞过程恢复系数模型研究

郭 振， 陈 渭， 耿 煜， 刘 喆

(西安交通大学 现代设计及转子轴承系统教育部重点实验室，西安 710049)

在机械系统中，接触碰撞现象非常普遍[1]，恢复系数作为计算碰撞过程中接触力的重要参数，对于准确预测机械系统的动态特性、可靠性及摩擦磨损具有重要意义[2]。近几十年来，国内外关于恢复系数模型的研究相对较多[3-8]，但这些模型通常忽略恒定外力的影响，因此，仅适用于不受恒定外力或所受恒定外力相对较小的碰撞过程。根据Shen等[9]研究发现，当恒定外力足够大时，恢复系数受碰撞过程中恒定外力的影响极大，例如：在低速重载的间隙转动副中，转子与外圈之间的碰撞即受恒定外力的作用，同时又受法向速度的作用。

目前，针对恢复系数的研究主要分为弹性碰撞阶段、弹塑性碰撞阶段和塑性碰撞阶段。赫兹接触模型基于弹性力学和连续体力学的理论，精确建立了两个弹性球碰撞之间的关系，但该模型仅适用于弹性碰撞，对于有塑性变形的碰撞不再适用。Ma等结合赫兹模型和Johnson模型中力和侵入深度之间的关系，利用力和侵入深度的连续性及碰撞过程中的几何关系，推导出在弹塑性碰撞阶段力和侵入深度的关系。Jackson等[10]利用有限元模拟半球形与刚性平面之间的接触，获得了无量纲接触面积与接触力之间的经验公式，并根据能量守恒推导出碰撞过程的恢复系数模型。Chang等[11]基于微凸体塑性变形体积不变原则，通过简化获得塑性碰撞阶段的接触模型(CEB模型)，并与Ling利用该模型建立了恢复系数模型[12]。上述几种恢复系数模型通过不同的力和侵入深度关系，建立不同的恢复系数模型，但均未考虑恒定外力作用时对恢复系数的影响。

目前，国内外对于恒定外力作用下碰撞过程的研究相对较少，然而在多体机械系统中，当外力的影响足够大时，则外力对于碰撞过程的影响将不能被忽略，并且由于恒定外力的作用，导致碰撞过程中塑性变形增加，能量耗散增加，恢复系数减小。Shen等研究了恒定外力对碰撞过程中接触力的影响，并建立了恒定外力作用下的接触力模型，但该模型只是在计算过程中说明了恒定外力影响恢复系数结果，并未深入研究恒定外力作用下的恢复系数模型。

本文充分考虑了恒定外力对于碰撞过程中恢复系数的影响，利用赫兹模型求解弹性碰撞过程以及Jackson和Green的力和侵入深度关系模型求解弹塑性接触过程，建立了恒定外力作用下的恢复系数模型，并通过与目前已有恢复系数模型进行对比验证本文恢复系数模型的有效性。

1 建立计算模型

1.1 弹性加载接触模型

从初始接触到材料开始发生屈服的过程为弹性加载阶段，由于赫兹模型对于弹性碰撞过程的计算较为准确，因此，在该阶段采用赫兹模型来计算碰撞过程中的接触力和侵入深度的关系。其关系如下所示

(1)

1.2 弹塑性加载接触模型

随着碰撞过程中侵入深度的增加，当侵入深度达到临界侵入深度时，碰撞体的材料开始发生屈服，在这个阶段弹塑性变形开始发生，为确定由弹性到弹塑性的临界速度、临界侵入深度和临界接触压力。已有学者做过相关研究，Jackson和Green利用屈服强度准则获得了临界接触压力与屈服强度之间的关系，并通过曲线拟合获得经验公式

(2)

根据Johnson利用赫兹弹性接触模型求解的弹性阶段侵入深度的理论计算公式

(3)

结合式(2)和式(3)可得临界侵入深度计算公式

(4)

结合式(1)和式(4)可计算获得临界接触力Fc

(5)

通过上述计算公式可获得在碰撞过程中，由弹性碰撞进入弹塑性碰撞时的临界值，在进入弹塑性碰撞之后，由于塑性变形的产生，赫兹接触力模型将不再符合碰撞过程中的力与侵入深度的关系。而目前关于弹塑性碰撞接触力与侵入深度之间的研究相对较多，根据Quicksall的研究发现[13]，Jackson和Green模型可适用的弹性模量、屈服强度和泊松比范围比较广泛，因此，本文在弹塑性加载阶段，采用Jackson和Green模型中的接触力与侵入深度公式

(6)

关于材料硬度几何极限与屈服强度之间的关系，根据文献[10]可知，当0

(7)

(8)

X=0.14exp(23*εy)

(9)

(10)

式中：HG为材料硬度几何极限；Aeq为等效接触面积；a为接触半径；

1.3 弹性卸载接触模型

当接触力和侵入深度达到最大时，碰撞体之间开始有分离趋势，进入卸载阶段。在卸载期间，接触体的分离过程被假设为弹性行为，利用赫兹模型做近似求解，同时根据Jackson等关于残余深度的有限元计算结果[14]，建立弹性卸载接触模型，其表达式如下所示

(11)

(12)

(13)

式中：Rres和wres分别为碰撞结束后的残余等效半径和残余深度。

1.4 恢复系数

目前关于恢复系数的定义主要是基于牛顿运动学恢复系数、Poisson定义的动力学恢复系数和Stronge定义的能量恢复系数[15]。根据文献[10]可知，在考虑外力作用的冲击过程时，Stronge能量恢复系数具有较好的计算结果，因此，本文采用Stronge定义的能量恢复系数

(14)

式中：W1和W2分别代表压缩和恢复阶段接触力所做的功。

1.5 恒定外力的影响

考虑两碰撞体分别在同一方向恒定外力Fi和Fj作用下的法向对心碰撞，其中两碰撞体的质量分别为mi和mj，则外力作用下的等效外力为

Fe=mea

(15)

me=m1m2/(m1+m2)

(16)

a=F1/m1-F2/m2

(17)

式中：me为两碰撞体的等效质量；a恒定外力作用下的相对加速度。

由式(15)可知，在恒定外力的作用下可能发生三种碰撞情况，即a>0，a=0和a<0，分别代表着加强碰撞、不影响碰撞和减弱碰撞，本文研究是关于a≥0的情况下恒定外力对恢复系数的影响。

(18)

式(18)用来考虑等效恒定外力的影响因子，在a≥0的情况下，其ε的取值范围0≤ε<1。

传统恢复系数模型认为恒定外力相对于碰撞过程中的接触力较小，因此通常忽略恒定外力的影响。根据图1中接触力和侵入深度关系可以发现，曲线的包围面积代表能量耗散的大小，而碰撞过程中的能量耗散用恢复系数表示，故在较小的初始速度下恒定外力对碰撞过程中的恢复系数影响较大，而当初始速度较大时，恒定外力的影响逐渐减小，可以忽略外力影响，这与传统恢复系数模型理论相同。因此，本文的研究应用主要集中在低速重载的碰撞过程。

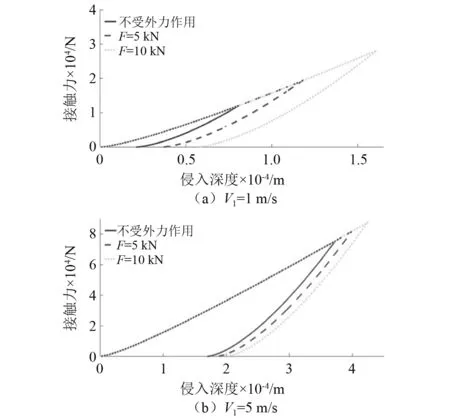
图1 恒定外力对接触力的影响

1.6 弹性压缩阶段

对于弹性碰撞过程，发生在开始接触到侵入深度达到临界侵入深度时，在该碰撞过程中由于能量损失主要是通过应力波的形式传播并且相对较小，故在一般计算过程中认为弹性碰撞没有能量损失。同时由式(4)可知，临界侵入深度只与屈服强度、弹性模量和碰撞体半径有关，因此，在碰撞过程中，恒定外力的作用并不影响材料的临界侵入深度，故本文在后面的研究中通过临界侵入深度判断碰撞发生的阶段。在弹性压缩阶段，外力作用下的弹性变形过程中的能量守恒公式如下所示

(19)

式中：V为碰撞过程中某一时刻的速度；V1为初始接触速度；w为某一时刻对应的侵入深度。

结合式(1)和式(19)可得

(20)

积分后得

(21)

通过计算可得弹性碰撞过程中的速度公式

(22)

随着弹性压缩阶段的结束，材料开始有塑性变形发生，此时碰撞体的侵入深度大于临界侵入深度，进入弹塑性碰撞阶段。为确定进入弹塑性碰撞阶段时的碰撞体速度，将w=wc代入式(22)中可得

(23)

该计算结果为在恒定外力和初始速度作用下，达到临界侵入深度时的速度计算公式。为确定碰撞过程中碰撞开始进入弹塑性碰撞阶段时的临界初始速度，即临界速度为0时的碰撞初始速度

(24)

结合式(4)和式(24)可得

(25)

式中：Vy为临界初始速度，当V1Vy时则该碰撞进入弹塑性碰撞阶段。

1.7 弹塑性压缩阶段

在碰撞过程中，随着侵入深度的增加，当侵入深度大于临界侵入深度时，碰撞进入弹塑性阶段。碰撞过程开始有塑性变形发生，并且随着侵入深度的增加，其接触力与侵入深度的关系不再符合赫兹接触力模型，需要引入式(10)所示的接触力随侵入深度变化关系。

在碰撞过程中初始动能及恒定外力所做的功均通过碰撞体接触部分的变形转化为碰撞体的应变能，因此，在弹塑性碰撞阶段，碰撞体的应变能变化的计算公式为

(26)

结合式(23)和式(26)可得

(27)

当碰撞达到最大侵入深度wm时，则此时V=0，初始速度与侵入深度的关系式为

(28)

1.8 弹性回弹阶段

当侵入深度达到最大侵入深度wmax时，此时碰撞体之间的相对速度为0 m/s，弹塑性碰撞阶段结束，碰撞体之间开始分离，进入恢复阶段，目前大多数研究均假设在卸载阶段接触力和侵入深度之间的关系为弹性的，因此，采用赫兹接触力模型作为恢复阶段接触力的计算。由于弹塑性碰撞过程中，有塑性变形发生，因此在碰撞结束后，接触表面出现残余深度wres，其计算公式见式(12)。将其代入赫兹模型回弹阶段的计算公式，其计算公式为

(29)

在恒定外力作用下，碰撞体之间分离时的相对速度计算式为

(30)

根据式(30)可得

V2=

(31)

式中：V2为碰撞体碰撞后分离时的速度。

2 结果与分析

2.1 恒定外力对恢复系数的影响

以经典单球碰撞模型为研究对象，如图2所示。将一质量为0.01 kg，半径为0.006 75 m的小球以不同初始速度开始下落，其中小球和平板的弹性模量均为210 GPa，泊松比为0.27，材料屈服强度为450 MPa。根据上述计算公式求解在不同恒定外力作用下的恢复系数，其计算结果，如图3所示。

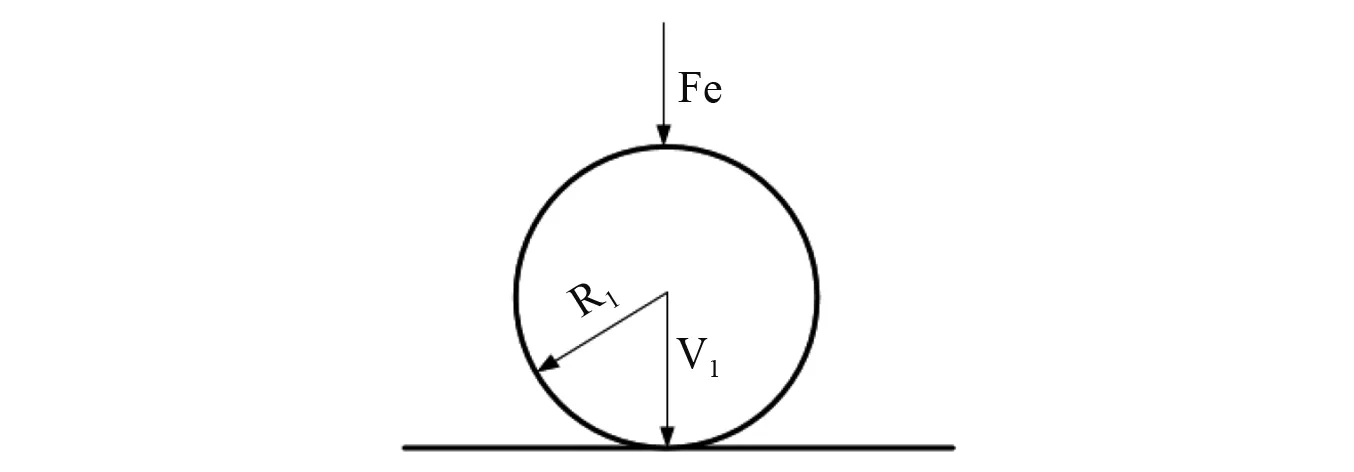
图2 单球碰撞模型

从图3(a)中可以观察到，在不同恒定外力作用下，恢复系数随恒定外力的增加逐渐减小，主要是由于在恒定外力作用下，使得碰撞过程中塑性变形增加，从而导致能量耗散增加，恢复系数逐渐减小。从图3(b)中可以观察到，不同初始接触速度下，恒定外力对于初始速度较小时的碰撞影响较大，这与图1分析结果相同，由于较小初始速度时，随着恒定外力的增加，初始速度所产生的接触力几乎可以忽略，故恒定外力对较低速度碰撞时的恢复系数的影响较大，这同Shen等在关于恒定外力作用下对碰撞的影响研究结果一致，其三维综合图如图3(c)所示。

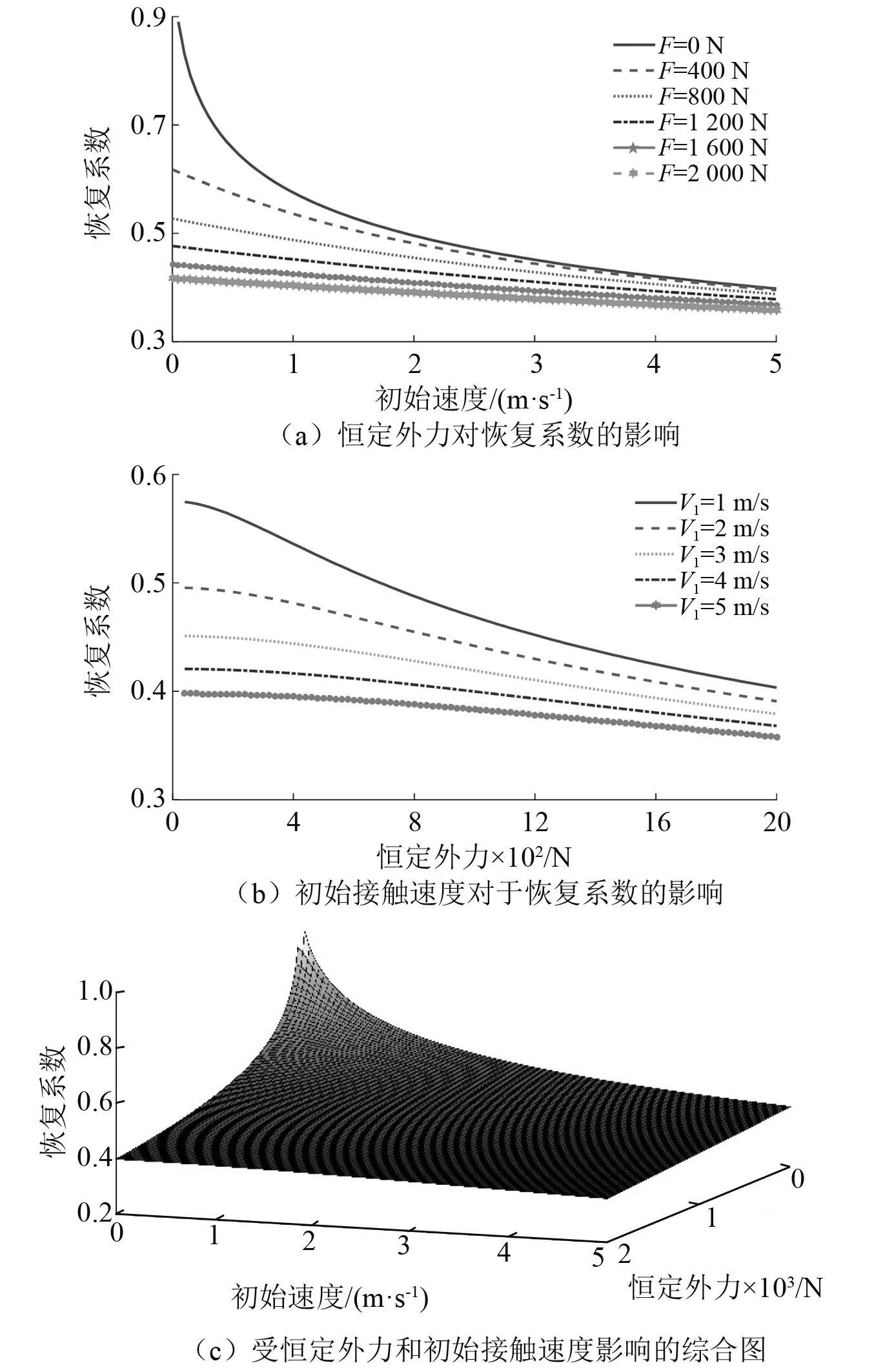
图3 恢复系数受恒定外力和初始接触速度影响图

目前关于恢复系数模型的研究中，Jackson等通过实验对比了J-G模型、Thornton模型和Wu模型，认为J-G模型在预测弹塑性碰撞阶段恢复系数时相对较为准确。为考虑恒定外力在连续碰撞过程中对侵入深度和侵入速度的影响，利用J-G模型与本文提出模型进行对比，对比结果如图4和图5所示，其中采用Shen等提出的受恒定外力作用下的接触力模型作为碰撞过程中接触力的计算，恒定外力为1 000 N,初始速度为0.5 m/s。

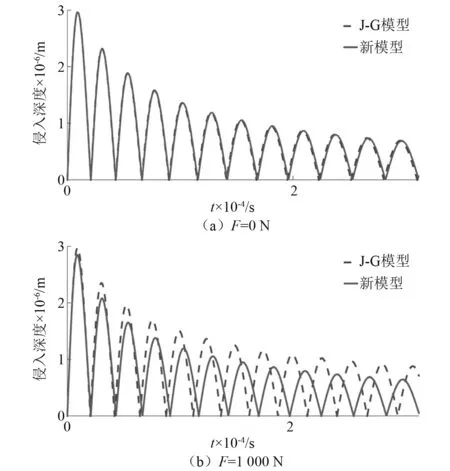
图4 连续碰撞过程中侵入深度图

图5 连续碰撞过程中侵入速度图

通过对比可以发现，在不受外力作用时，两模型在侵入速度和侵入深度上具有较好的一致性，这也验证了本文模型在不受外力作用时模型的有效性。当受恒定外力作用时，由于J-G模型不考虑恒定外力的影响，而本文模型在恒定外力的作用下恢复系数减小，因此，在发生碰撞时，本文模型侵入深度与分离速度均下降，并且在连续碰撞过程中，随着每次碰撞后计算结果的累积，使得两模型结果相差逐渐增大。最终当初始速度较低时，碰撞过程进入弹性碰撞阶段，两模型达到稳定，而本文模型由于考虑恒定外力的作用，因此，本文模型达到稳定时的初始速度相对较小。

2.2 对比目前的恢复系数模型

根据其连续碰撞过程可以发现，首次碰撞结果对其后碰撞影响较大，因此，进一步对比研究在首次碰撞过程中，本文模型与目前恢复系数模型在碰撞过程中的侵入深度及速度变化。根据式(32)中受恒定外力作用时的等效动力学方程，计算在碰撞过程中恒定外力的影响。由于Shen等受恒定外力的接触力模型在不同恢复系数作用下，恢复系数具有较好的回归性，因此，等效动力学方程的阻尼因子采用Shen等的阻尼因子模型，恢复系数模型采用传统J-G模型，其中碰撞体的材料参数半径为0.02 m，质量为0.26 kg，刚度1.4×108N/m1.5为，屈服强度为450 MPa，初始接触速度V1为0.5 m/s。

(32)

求解动力学方程式(32)，在不同的恒定外力影响因子下，如图6所示，随着恒定外力的增加，其侵入深度增加，材料塑性变形增加，导致碰撞后的分离速度减小，当恒定外力足够大时，其碰撞后不发生分离。而目前的恢复系数模型均忽略恒定外力的影响，以碰撞后的分离速度与初始速度之比定义恢复系数，在恒定外力足够大时，传统恢复系数模型的预测结果是不准确的，因而恢复系数模型须考虑恒定外力的影响。

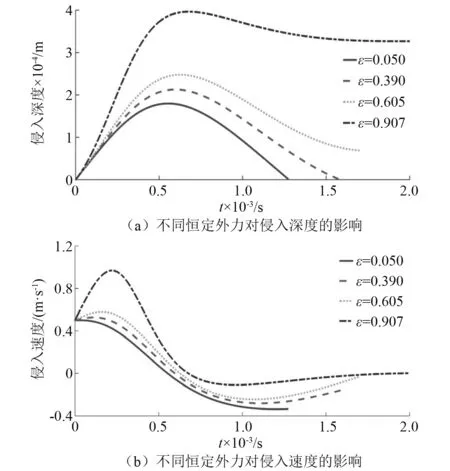
图6 不同恒定外力对碰撞过程的影响

目前，关于恢复系数模型的研究相对较多，均通过不同的接触力和侵入深度关系，结合碰撞前后能量守恒定律推导获得恢复系数模型，其中Thornton模型通过假设弹塑性阶段接触力与侵入深度关系，获得恢复系数模型，Wu模型利用有限元软件仿真研究碰撞前后分离速度，并通过拟合曲线获得恢复系数模型，J-G模型通过仿真得到弹塑性阶段接触力和侵入深度关系，获得恢复系数模型并通过实验验证，但均未考虑恒定外力的影响。为对比恒定外力作用下，本文模型与目前已有模型在碰撞过程中的变化，取恒定外力影响因子分别为0.05、0.39、0.605和0.907，其恒定外力分别为10 N、100 N、200 N、800 N，计算结果如图7、图8所示。

图7 不同模型时间与侵入深度的关系

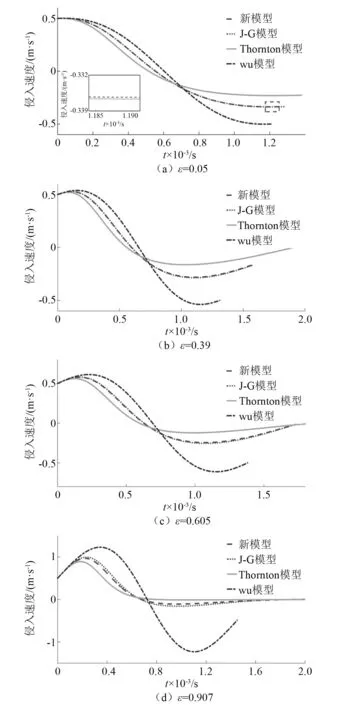
图8 不同模型时间与侵入速度的关系

如图7所示，通过对比可以发现，在相同恒定外力及初始速度作用下，Wu模型侵入深度最大，主要是由于Wu模型在初始速度较低时，过高预测恢复系数，因而导致其碰撞过程中，每一时间步，能量耗散减少，侵入深度增加，而Thornton模型过低预测恢复系数[16]，使得能量耗散增加，侵入深度减小。J-G模型通过实验验证了其恢复系数模型的有效性，与本文模型在受力较小时具有很好的一致性，但随着恒定外力的增大，本文模型恢复系数逐渐减小，因而导致最大侵入深度低于J-G模型预测结果。并且在图7(d)中当恒定外力足够大时，其碰撞后碰撞体不发生分离。

如图8(d)所示，在恒定外力的作用下，当碰撞体初始接触时，由于接触力小于恒定外力，碰撞体速度先增大，当接触力等于恒定外力时，碰撞体加速度为零，之后速度开始减小，在分离阶段随着接触力减小，碰撞体速度增大，当接触力小于恒定外力时，恒定外力使得碰撞体速度减小，直至彻底分离。由于Wu模型预测恢复系数较大，因而碰撞后，Wu模型的分离速度最大，而Thornton模型、J-G模型及本文模型分离速度均为0 m/s，即碰撞后不发生分离，这表明考虑恒定外力通过碰撞前后的能量之比定义恢复系数是更加有效的。根据图8可知，随着恒定外力的增加，恒定外力对本文恢复系数模型的影响逐渐增大，而传统恢复系数模型不受恒定外力影响，故随着恒定外力的增大，本文模型与J-G模型预测的侵入速度之间的差值逐渐增大。

根据图8可以发现，在碰撞过程中，本文模型与J-G模型侵入速度曲线较为一致，进一步对比两模型预测的能量耗散之间的关系，结果如图9所示，本文模型在初始速度较小时，恒定外力越大对应的恢复系数越小，能量耗散越大，主要是由于恒定外力越大，侵入深度增大，弹塑性变形增大，能量耗散增多。而J-G模型不考虑恒定外力的影响，恢复系数结果不随恒定外力改变，因而不符合实际情况。

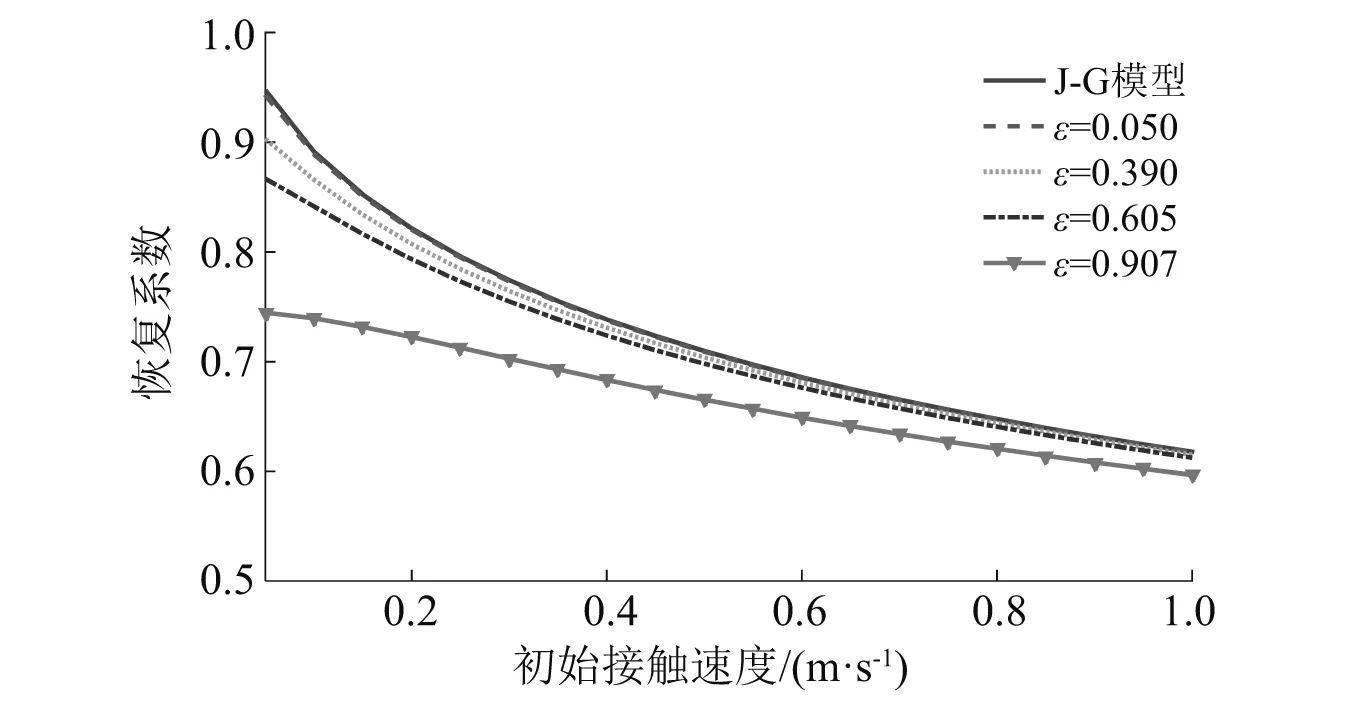
图9 J-G模型与本文模型结果对比

2.3 经验公式

根据碰撞过程中的恢复系数计算公式，简化式(6)获得简化后的弹塑性阶段接触力与侵入深度之间的关系如式(34)所示，根据Williams[17]的研究式(7)的可取理论值式(33)，该简化过程是导致简化恢复系数模型误差的主要原因，如图10所示，模型适用于1.9<(w*)m<800范围内的恢复系数预测，简化后的恢复系数模型如式(35)所示，其误差最大为8.6%，平均为3.2%，符合实际工程应用，其中弹塑性碰撞阶段的最大侵入深度可通过式(36)获得。

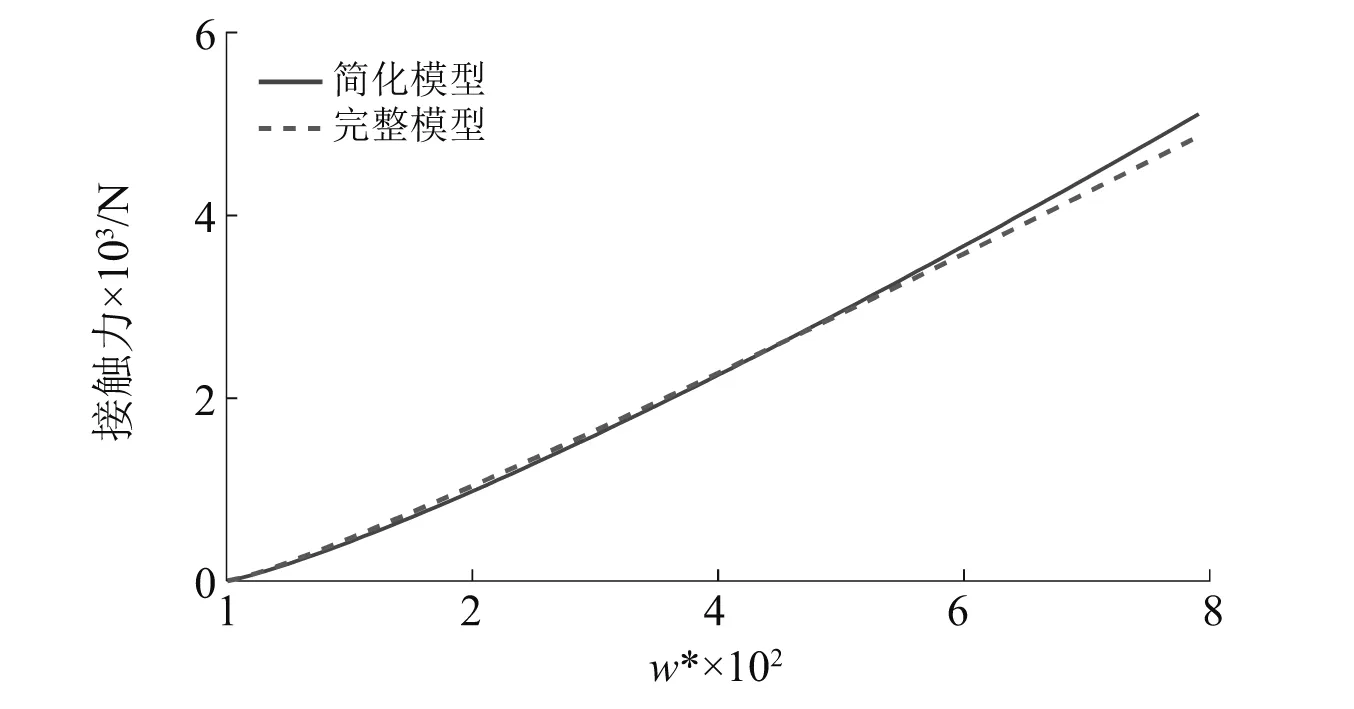
图10 简化模型

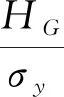
(33)

(34)

Cr=

(35)

(36)

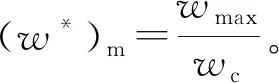
3 结 论

针对弹塑性碰撞体受恒定外力作用时初始速度对恢复系数的影响，本文建立了一种恒定外力作用下弹塑性碰撞阶段恢复系数的预测模型,结果如下：

(1) 通过对比接触力和侵入深度之间的关系，在低速重载工况下，考虑恒定外力对恢复系数的影响具有重要意义，且随着恒定外力的增加，碰撞过程塑性变形增加，恢复系数显著降低。

(2) 传统恢复系数模型区分不同碰撞阶段均通过临界初始速度，为考虑恒定外力的影响，本文通过临界侵入深度进行区分，同时考虑了恒定外力与初始速度的共同作用。

(3) 通过连续碰撞过程可以发现恒定外力作用下恢复系数对接触力计算具有重要意义，同时，对比分析在不同恒定外力作用下的四种恢复系数模型，可以发现，通过碰撞前后的能量比定义恢复系数，考虑恒定外力的影响，能更加有效的预测碰撞恢复系数。

(4) 为提高计算效率，便于实际工程应用，通过简化理论推导过程，归纳并获得简化后的经验公式，并对比理论计算，获得其最大误差为8.6%，平均为3.2%。