一种信号分析研究装置的设计
2021-06-30天水师范学院电子信息与电气工程学院王睿庭
天水师范学院电子信息与电气工程学院 王睿庭
设计了一种以STM32单片机为核心的信号分析研究装置,能够分析测量信号的频率及幅度,可测量信号各谐波分量的幅值,进而测量计算信号的失真度,还可实现常见波形信号如正弦波、方波、三角波和锯齿波的频谱显示,具有成本较低,显示直观,测量精度较高等优点,达到设计要求。
信号分析在各个领域有着广泛的应用,比如频谱分析、失真度测量,专用仪器往往价格昂贵而且功能单一,传统的模拟频谱分析仪由于体积庞大、成本高、反应速度慢已不适应时代需求,而快速傅里叶变换(FFT)可以将时域信号变换到频域来分析、处理,运算速度大大提高。本文设计了一种信号分析研究装置,不仅能测量信号的频率和幅值,还能进行频谱分析,测量信号的失真度。该装置实用性较强,具有一定的应用价值。
1 理论分析与计算
1.1 FFT算法
离散傅里叶变换(DFT)是数字信号分析与处理中的一种重要且非常有用的变换,它将信号在时域和频域都离散化了,非常适于对离散信号的分析与处理。但是直接计算DFT的运算量与变换区间长度N的平方成正比,当N较大时,运算量会急速增大,从而影响运算速度。而DFT的快速算法即快速傅里叶变换(FFT)的出现,大大提高了离散傅里叶变换的运算速度,如基2FFT算法的运算量减少为(N/2)*log2(N)。更重要的是,通过快速傅里叶变换可以将信号从时域变换到频域,进而进行频谱分析,这就是很多测量仪器采用FFT的原因。利用FFT可得到一个信号的频率、幅值及相位信息,亦可得到各次谐波分量的幅值、相位信息。
假设采样频率为Fs,信号频率为F,采样点数为N。则FFT运算之后结果是N点的复数,每个点对应原来信号的一个频率点。若某点n用复数a+bi表示,那么这个复数的模为,相位为Pn=atan2(b,a),频率就是:

其中,N表示FFT要做的点数,n表示排序的点,Fs为采样频率。
对于n=1点的信号,对应信号的直流分量,幅度为A1/N。
1.2 失真度测量
由信号失真度的定义可知,全部谐波能量之和与基波能量之比的平方根值即为信号的失真度,即:

式中,P为信号总能量,P1为信号的基波能量。
当负载为纯电阻负载时,信号的失真度也可用下式来表示:
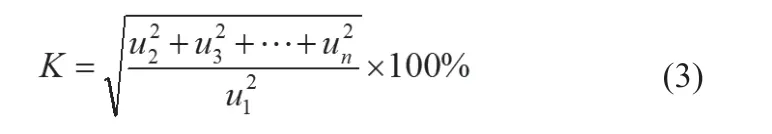
式中:u1为基波电压的有效值,u2,u3,…,un为各次谐波分量的有效值。本设计中为了方便设计,谐波只取到5次。
2 硬件设计
系统总体设计框图如图1所示。
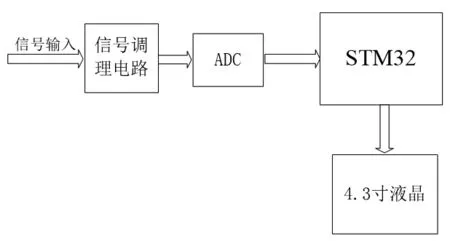
图1 系统总体设计框图
待测信号由信号发生器提供或经过放大电路放大后输入,信号调理电路主要包括信号抬升电路及滤波电路等,作用是将待测信号加入直流偏移以适合作为STM32的ADC输入电压范围(在0-3.3V之间),同时滤除干扰杂波信号,保证测量的准确性,之后信号经过AD转换后在STM32内部实现FFT运算变换,进行频谱分析、数据处理后显示在4.3寸液晶屏上,可显示信号频率、幅度、各谐波分量的幅值及失真度等。
STM32单片机采用意法半导体(ST)公司的增强型STM32F103系列,嵌入Cortex-M3内核,主频可达72MHz,具有512KB的片上Flash存储器和64KB的SRAM存储器,内部包含2个12位的逐次逼近型A/D转换器,多达18个通道,转换时间接近1us。
3 软件设计
主程序流程图如图2所示。主程序总体设计思路是:系统上电后单片机内部进行复位,对TIM1、ADC、DMA、液晶屏等外设进行初始化,对待测信号进行AD转换后通过DMA将数据搬运至内存,等待DMA产生中断后再进行FFT运算,完成频谱分析后将结果显示在4.3寸液晶屏上。
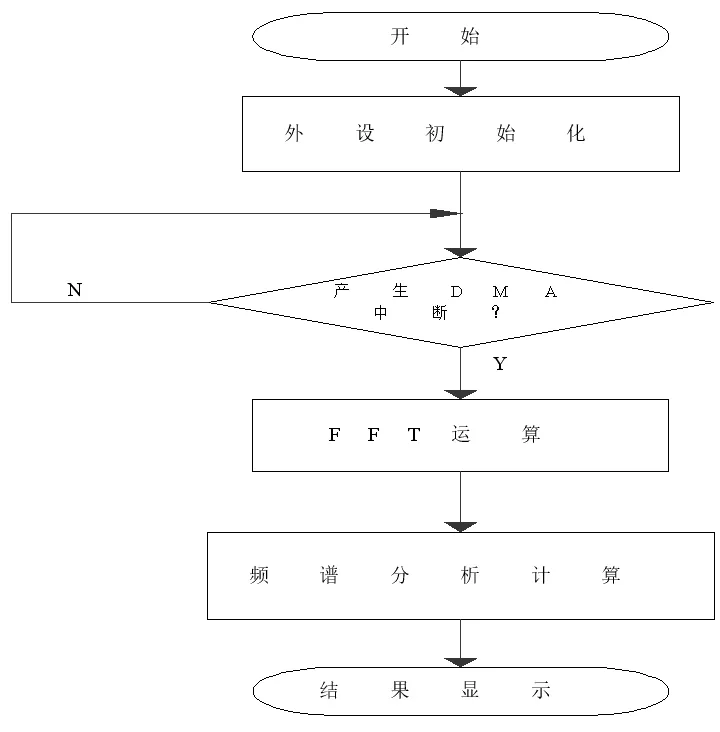
图2 主程序流程图
3.1 ADC采集
使用TIM定时器触发AD采集,此处通过TIM1的通道1产生PWM信号来触发AD采集,PWM的频率也就是ADC的采样频率。根据奈奎斯特采样定理可知,被测信号频率最大值要小于或等于采样频率的二分之一。由于STM32芯片内部ADC的采样率最高为1Mhz/s,采样位数为12位,所以待测输入信号频率最高可以到500Khz,能够用在一些频率不高的场合。
3.2 DMA配置
AD采集一定数量的点数之后产生DMA中断,然后通过DMA将数据搬运至内存。因为采用中断方式,且DMA传输过程不需要CPU干预,可以有效地降低CPU负荷,提高系统运行速度。本设计使用DMA1的通道1,传输数据量为1024。
3.3 FFT算法
通过单片机内部的DSP进行运算处理,由于Cortex M3内核的CPU没有FPU及DSP指令,这里使用ST官方的汇编FFT库,因为这个库是汇编的,而且是基4算法,所以执行效率非常高效,运算速度较快。
进行1024点的FFT,只需要调用DSP库函数中的cr4_fft_1024_stm32()函数即可。该函数调用的格式为:
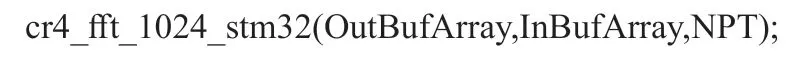
其中,OutBufArray表示FFT运算的输出数组,InBufArray表示要进行FFT运算的输入数组,也就是ADC采集的数据,NPT表示采样点数。
按照ST官方库的说明,OutBufArray和InBufArray都必须是32位的数据类型,其中高16位存储实部,低16位存储虚部。
FFT的分辨率为Fs/N,要减小误差可增大N,本设计用到的采样点数N为1024,采样频率Fs越大分辨率就越低,误差就越大,因此在测量低频信号时应该降低采样频率,最低需大于信号频率的两倍。
4 测试结果
4.1 信号频率与峰峰值的测量
从信号发生器输入不同频率、幅值的正弦波,测试结果如表1所示。
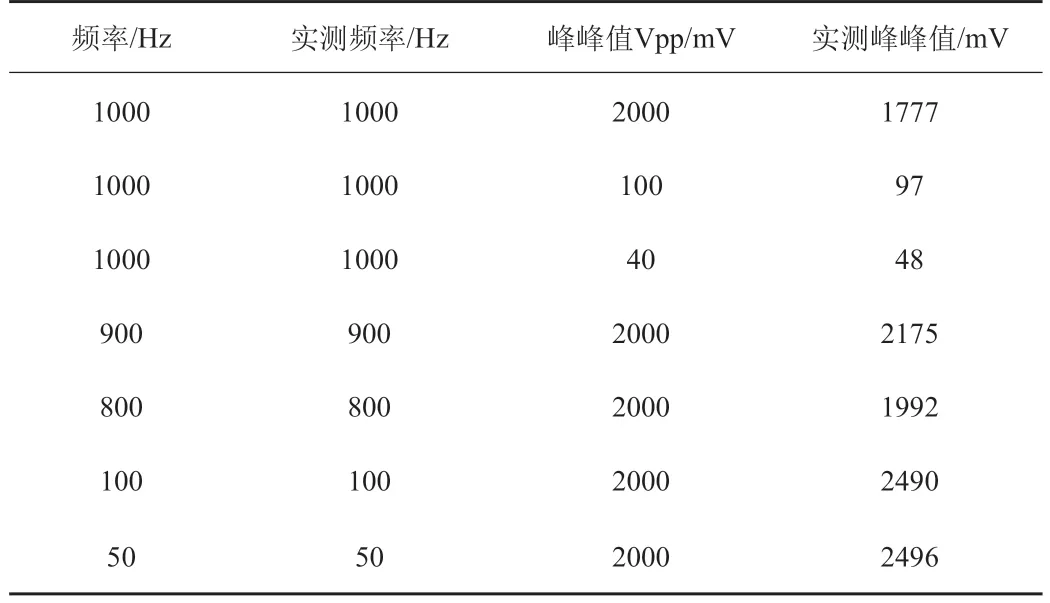
表1 不同频率、幅值的正弦波测试结果
4.2 失真度测量
分别从信号发生器输入2Vpp、1KHz的正弦波、方波和三角波,测试结果如表2所示。
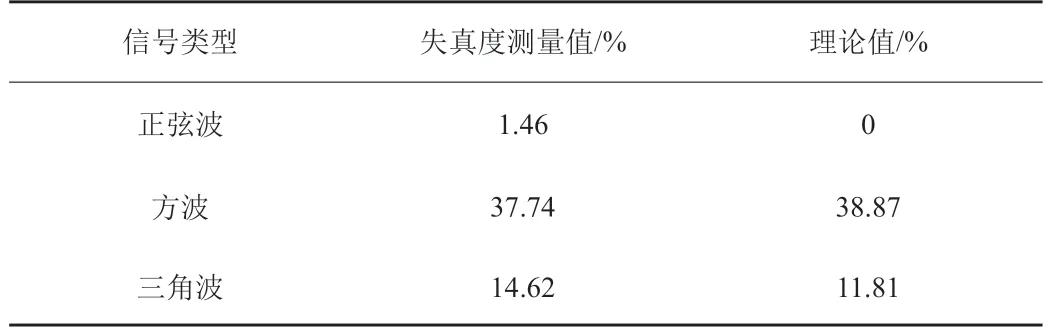
表2 不同类型信号失真度测试结果
4.3 测试结果分析
通过测试,该装置测量信号频率的精度很高,测量信号失真度的精度较高,对信号幅值的测量存在一定的误差,但对微弱信号也可以测量,精度较高,能够满足设计精度要求。
结语:本文设计并实现了一种基于STM32的信号分析研究装置,能够分析测量信号的频率及幅度,可测量各谐波分量的幅值,进而测量计算信号的失真度,还可实现常见波形信号如正弦波、方波、三角波和锯齿波的频谱显示,测试结果表明,本装置所测数据精度较高,各项指标均达到了设计要求。
