不同孔隙率碳纤维增强环氧树脂复合材料板的压缩强度及其预测模型

杨鹏飞，樊俊铃，宁 宁，史俊伟

(1.中国飞机强度研究所，西安 710065；2.中航复合材料有限责任公司，北京 101300)

0 引 言

树脂基复合材料(以下简称复合材料)在飞机结构中的应用量较大[1]，波音787飞机结构中复合材料的质量达到全机总质量的50%以上，空客A350飞机结构中复合材料的占比高达52%。在飞机复合材料结构件的制造过程中，固化温度、压力、时间等参数控制不合理会造成树脂挥发，使得树脂未完全浸润纤维，纤维中的空气没有完全排出，而产生孔隙。孔隙的产生会影响复合材料结构件的拉伸、弯曲、层间剪切以及压缩等性能。

YOSHIDA等[2]研究表明，碳/环氧复合材料中的孔隙降低了层间剪切强度、拉伸强度以及压缩强度。GÜRDAL等[3]建立了AS4石墨/3501-6环氧树脂复合材料层间拉伸强度的指数型预测模型，研究了孔隙率对层间拉伸强度的影响。SUAREZ等[4]研究发现，孔隙率为4%时，单向碳/环氧树脂复合材料的压缩强度较孔隙率为0的明显下降。ALMEIDA等[5]在Mar-Lin方程的基础上建立了衰减系数和弯曲强度的关系，得到F584碳纤维/环氧树脂编织复合材料层压板弯曲强度的预测模型。刘玲等[6]研究了孔隙率对T700碳纤维/TDE环氧树脂复合材料拉伸、弯曲及层间剪切性能的影响。梁少旭[7]分析了孔隙率对T300碳纤维/BMP-316环氧树脂复合材料层压板压缩性能的影响。朱洪艳[8]采用GÜRDAL等建立的模型预测了T300碳纤维/914环氧树脂复合材料的压缩强度并进行了试验验证。程家林等[9]采用细观力学方法研究了孔隙率对AS4石墨/3501环氧树脂复合材料层合板压缩强度的影响。齐泽文等[10]基于双尺度分析方法模拟了孔隙数量及其位置对三维四向纤维/环氧树脂编织复合材料拉伸性能的影响，结果表明孔隙数量对复合材料拉伸性能的影响较大，孔隙位置对拉伸性能的影响不大。

目前，通过试验建立的含孔隙复合材料压缩强度的理论预测模型还不够完善和准确。作者对不同孔隙率IMA碳纤维增强M21环氧树脂复合材料板进行了压缩试验，在前人研究的基础上，对压缩强度的指数型预测模型进行了改进，建立了更加精确的适用于该复合材料的压缩强度预测理论模型，为实际工程应用提供参考。

1 试样制备与试验方法

试验材料为中航复合材料有限责任公司生产的IMA碳纤维增强M21环氧树脂复合材料板，铺层顺序为[45/45/0/90/0/90]s，尺寸为300 mm×150 mm×2 mm，单向带预浸料的力学性能参数如表1所示。

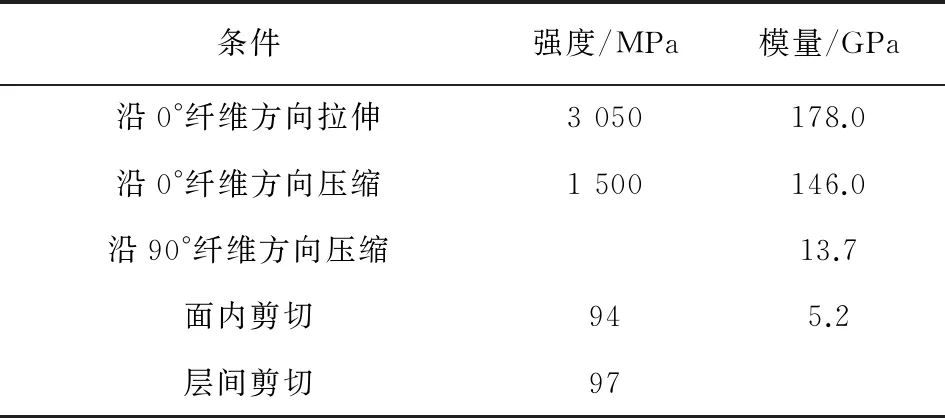
表1 单向带预浸料的力学性能参数

基于反射法测量复合材料板的超声衰减量，表达式为

(1)

式中：Vf为复合材料板单个点的上表面波幅；Vb为复合材料板单个点的背表面波幅；A为超声衰减量。

采用MUT-1型超声检测设备及5 MHz超声检测探头获得8块复合材料板的上表面波幅和背表面波幅，每块复合材料板测100个点取平均值。根据衰减量和孔隙率之间的关系[11]计算孔隙率，表达式为

A=(1.38+1.08ν2)t+2.76

(2)

式中：ν为孔隙率；t为复合材料板的厚度。

通过超声检测获得各复合材料板的平均超声衰减量分别为5.52，5.92，9.28，10.00，10.58，13.07，17.25，18.17 dB，计算得到复合材料板的平均孔隙率分别为0，0.43%，1.32%，1.44%，1.53%，1.87%，2.33%，2.42%。根据ASTM D6641，在不同孔隙率复合材料板上分别沿0°和90°纤维方向截取尺寸为140 mm×12 mm×2 mm的无缺口压缩试样,如图1所示。在试样正面和反面中心位置贴应变片，以获取试样的应变。将试样安装在夹具内，拧紧夹具螺栓，拧紧力矩为3 N·m。将夹具和试样组合件放置在INSTRON 8801型压缩试验机的压缩平台上进行压缩试验，确保组合件的纵向轴线与试验机的纵向轴线重合，如图2所示，以1.3 mm·min-1的下压速度对试样进行压缩，直到试样破坏，记录此时的应变、位移和载荷。试验温度为(23±3) ℃，相对湿度为(50±10)%，每组试样进行6次平行试验。

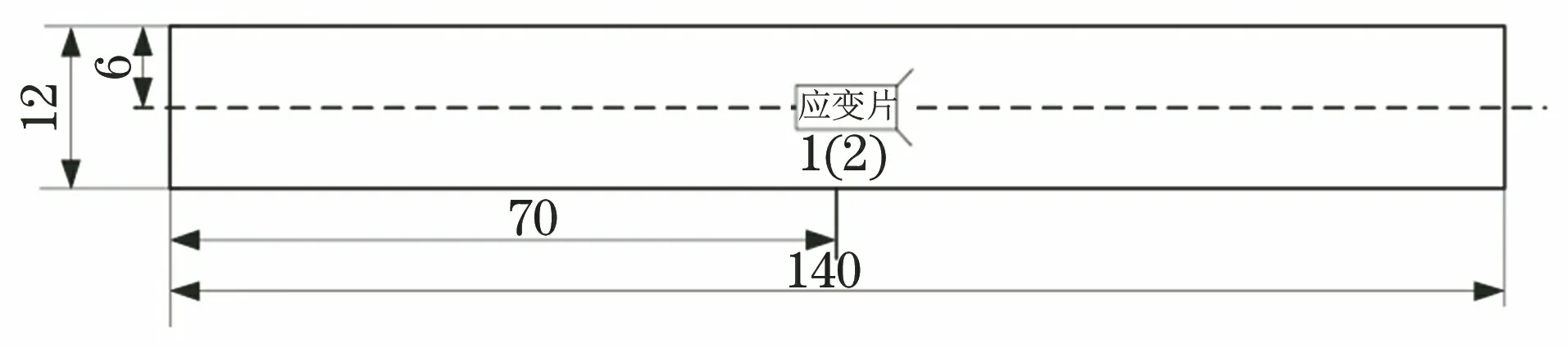
图1 压缩试样尺寸Fig.1 Dimension of compression sample

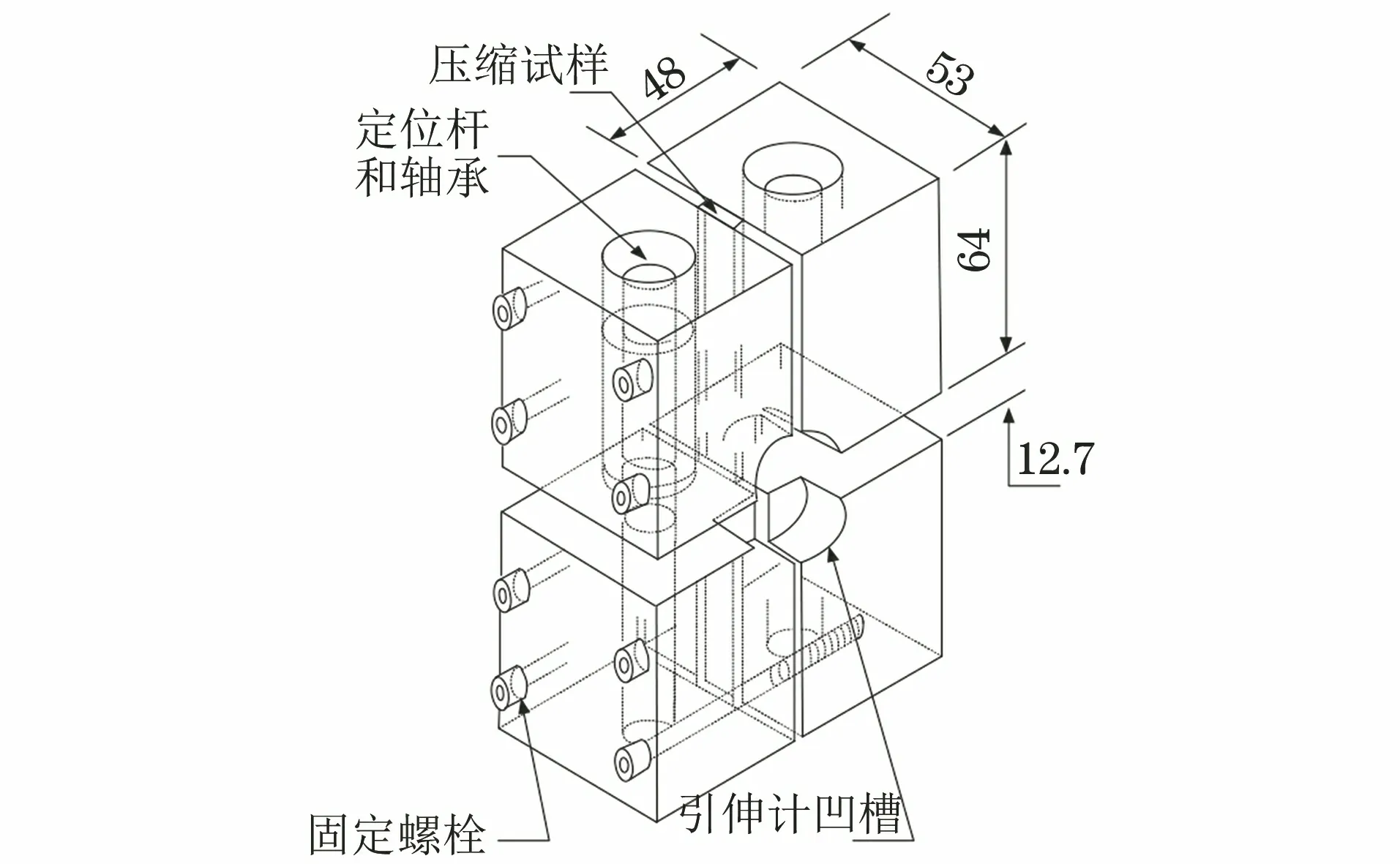
图2 压缩试样放置位置示意Fig.2 Diagram of position of compression sample

2 试验结果与讨论

2.1 载荷-位移曲线

由图3可以看出：初始阶段，载荷随位移增大几乎无变化，这是由于压缩过程中压头还未完全接触到试样；孔隙率不大于1.87%时，试样的最大载荷较孔隙率为0的变化不大，孔隙率为2.33%，2.42%时，试样的最大载荷较孔隙率为0的明显降低。

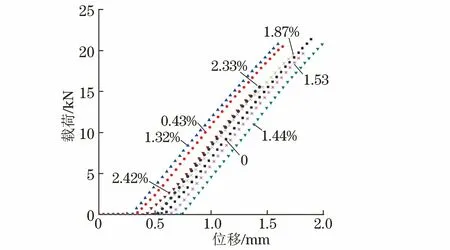
图3 不同孔隙率试样沿0°纤维方向压缩时的载荷-位移曲线Fig.3 Load-displacement curves of samples with different porosities in compression along 0° fiber direction

2.2 压缩强度

压缩强度的表达式为

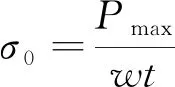
(3)

式中：σ0为压缩强度；Pmax为试样破坏前的最大载荷；w为试样实测宽度；t为试样实测厚度。

根据HB 7618—2013，对压缩强度进行正则化处理，即将试样的实测厚度修正为名义厚度得到正则化后的压缩强度，表达式为

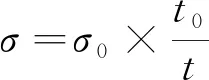
(4)

式中：σ为正则化后的压缩强度，MPa；t为名义厚度。

获得正则化的压缩强度后，计算其平均值、标准差和离散系数等统计特征量，表达式分别为

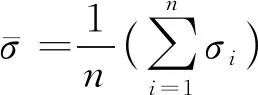
(5)

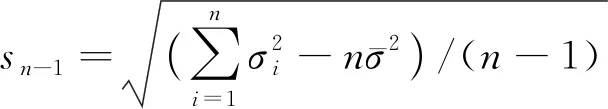
(6)

(7)

复合材料板的孔隙不均匀，在同一孔隙率复合材料板上截取压缩试样时，由于标准压缩试样的尺寸较小，存在压缩试样孔隙率与整块板的平均孔隙率相差较大的问题，需采用最大赋范残差法剔除与真实孔隙率相差较大的孔隙率对应的压缩强度数据，最大赋范残差的计算公式为

(8)

式中：MNR为最大赋范残差。

每块复合材料板的压缩试样为6件，根据HB 7618—2013，取临界值1.887，MNR值大于1.887时，剔除该压缩强度数据，同时根据HB 7618—2013，将压缩强度的离散系数控制在10%以内，以保证数据的有效性，最终得到不同孔隙率试样正则化后的压缩强度平均值、标准差及离散系数，如表3所示。

由表2可以看出，孔隙率不大于1.87%时，压缩强度较孔隙率为0的下降不明显；孔隙率大于1.87%时，压缩强度较孔隙率为0的明显降低。孔隙率为0～1.53%试样的压缩强度相差最大为79 MPa，推测这是制造工艺存在差异造成的，此时孔隙率对压缩强度的影响不大；孔隙率达到1.87%及以上时，试样的压缩强度相差最大为297 MPa，此时孔隙率的增加是导致压缩强度大幅下降的主要原因。

表2 不同孔隙率试样压缩强度的统计特征量

3 压缩强度的预测模型

孔隙率达到临界值(1.87%)前，压缩强度随孔隙率的增大变化不大，达到临界值后，压缩强度迅速下降。压缩强度随孔隙率的变化趋势和Logistic曲线模型相似，在该模型基础上，作者提出了孔隙率和压缩强度的非线性关系模型，表达式为

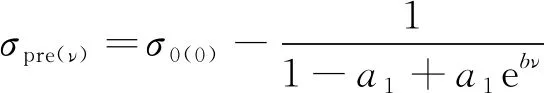
(9)

式中：σ0(0)为孔隙率为0时试样的实测压缩强度；σpre(ν)为孔隙率为ν时试样的预测压缩强度；a1和b为常数，与材料有关。

预测压缩强度和孔隙率之间关系的经典Gürdal模型的表达式为

σpre(ν)=σ0(0)e-a2ν

(10)

式中：a2为与材料相关的常数。

采用最小二乘法确定式(9)和式(10)中的参数a1，b，a2，通过使目标函数值达到最小，获得各参数值，目标函数Q的表达式为

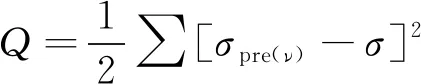
(11)

式中：Q为σpre(ν)与σ之间的均方差。

采用MATLAB中nlinfit函数自带的Levenberg-Marquardt算法确定目标函数的最小值，以孔隙率为输入值，正则化后的压缩强度为输出值。对于Gürdal模型，拟合得到0°纤维方向时，a2=0.093 7，90°纤维方向时，a2=0.075 4。同理，获得非线性模型中的a1，b参数值。随着孔隙率增加，压缩强度减小。为了保证孔隙率较大时，非线性模型预测得到的压缩强度与实际相符，不会出现负值，需要增加一组孔隙率为10%的压缩强度预测值。根据Gürdal模型预测孔隙率为10%时的压缩强度，基于该预测压缩强度，采用MATLAB编程，得到0°纤维方向时，a1=0.998 1，b=2.626 5，90°纤维方向时，a1=0.997 6，b=2.455 4。

由图4和图5可以看出，与Gürdal模型相比，试验数据点在非线性模型曲线附近的集中程度更高，说明非线性模型对压缩强度预测的准确性更好。试验结果与非线性模型曲线存在相差较大的数据点是由于制造的复合材料板孔隙不均匀，试样的取样部位不同，这些相差较大的数据点是该压缩试样孔隙率与整块复合材料板平均孔隙率存在差距但在最大赋范残差范围内对应的压缩强度，同时超声衰减法测量计算得到的孔隙率存在一定的人为误差，测量不够准确，此时得到的压缩强度与真实孔隙率对应的压缩强度也有差别，对拟合结果也会有一定的影响。

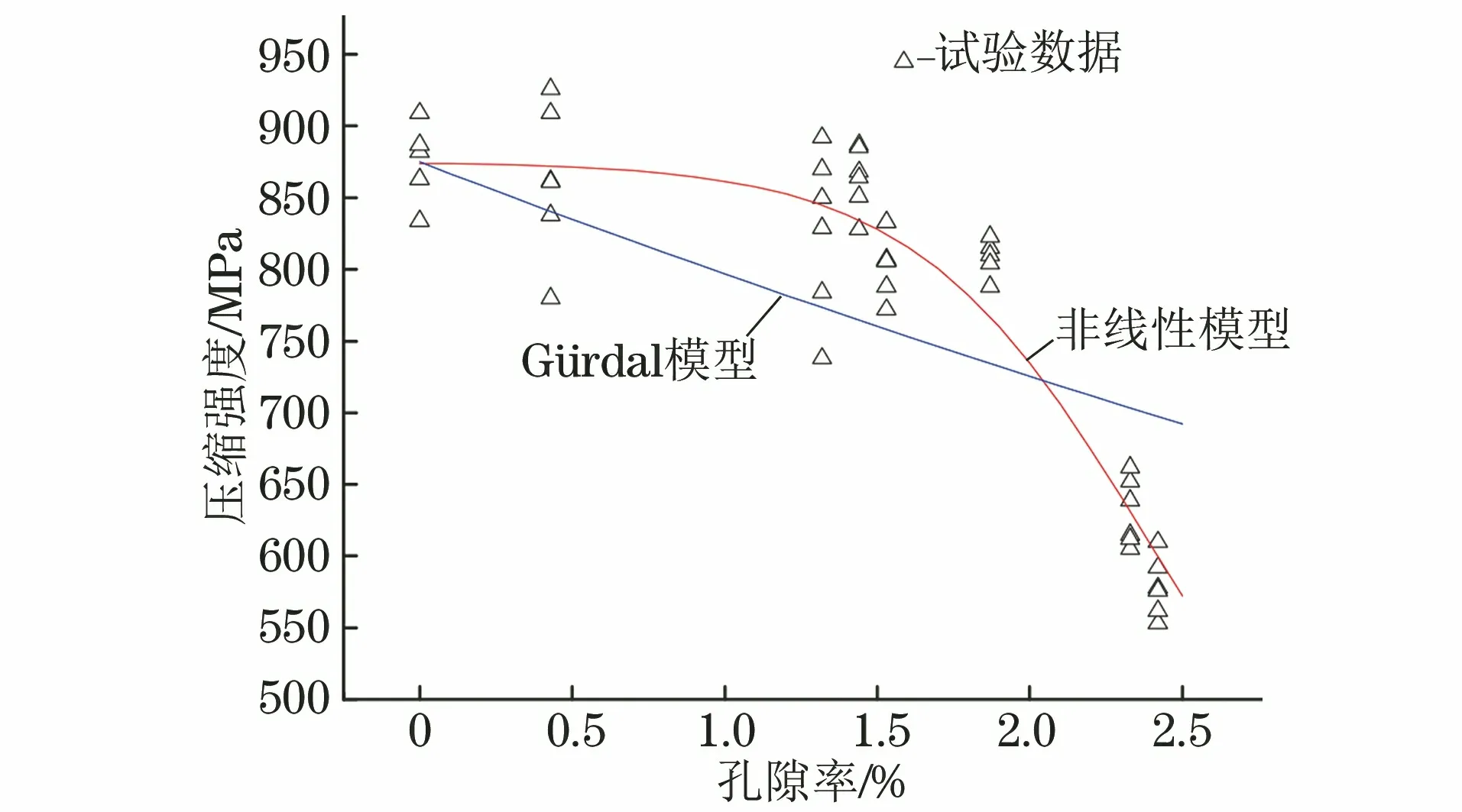
图4 沿0°纤维方向压缩时不同孔隙率试样的不同模型预测和实测压缩强度Fig.4 Predicted by different models and measured compressive strength of sample with different porosities compressed along 0° fiber direction

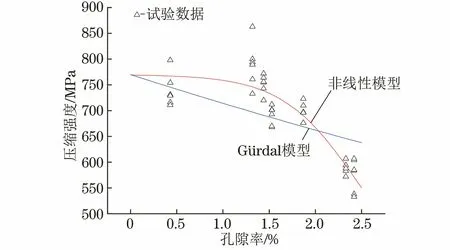
图5 沿90°纤维方向压缩时不同孔隙率试样的不同模型预测和实测压缩强度Fig.5 Predicted by different models and measured compressive strength of sample with different porosities compressed along 90° fiber direction

通过决定系数对模型预测的准确性进行评价，决定系数的计算公式为

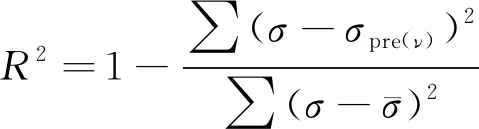
(12)

式中：R2为决定系数。

R2的值位于0～1，越接近1，说明预测结果越准确，越接近0，说明预测结果的准确性越差。由表3可以看出，非线性关系模型的决定系数相比于Gürdal模型更接近1，说明在试验复合材料板中，采用非线性关系模型预测的压缩强度较Gürdal模型具有更高的准确性。

表3 非线性模型和Gürdal模型的决定系数

4 结 论

(1) 孔隙率不大于1.87%时，IMA碳纤维增强M21环氧树脂复合材料板的压缩强度较孔隙率为0的变化较小，孔隙率对压缩强度的影响较小，孔隙率大于1.87%时，复合材料板的压缩强度较孔隙率为0的明显降低，此时孔隙率对压缩强度的影响较大。

(2) 建立的孔隙率和压缩强度的非线性关系模型的决定系数相比于Gürdal模型更接近于1，预测结果更准确。