三轴减速系统的转子动力学特性研究

于广滨，于皓南

（1.长春理工大学 机电工程学院，长春 130022；2.哈尔滨理工大学 机械动力工程学院，哈尔滨 150080）

多轴传动系统在许多高速转动机械中应用十分广泛，而且也是航空发动机、减速器等的核心部分。随着现代工业迅猛发展，转动机械逐渐趋向高转速、大功率。例如机床、发动机、减速器、膨胀机等各种工程机械和许多其他的重要工业机械设备均属于转动机械。通过齿轮啮合的多轴转子系统作为转动机械的核心部分，由于其传动平稳、传动效率高、传动比精确、结构紧凑、传递功率恒定等特点，具有其它传动无可替代的优势，被广泛应用在汽车、化工、航空、航天和船舶等行业的重要设备中，这些设备的安全、可靠、稳定的运行才能保证社会的快速发展。多轴转子系统动力学是一门应用性科学，它研究转子的各种动力学特性和动力学现象，是转动机械动力学问题的核心内容。

转子系统的动力学研究已经有很长一段时间，张兆丰［1-2］通过研究压缩机中五轴齿轮耦合转子系统发现，齿轮啮合是导致转子系统振动的主要原因。王志强等人［3］研究了船舶轮机中齿轮箱中齿轮耦合转子系统的转子动力学特性，对比了齿轮耦合与非耦合情况下系统动力学特性的不同。宋涛［4］建立了振动轴-转子系统的振动微分方程，并分析了转子系统的“失步”现象。邢印［5］基于API684标准对电机转子的横向动力学进行分析与校核。虞磊［6］使用了有限元法和实验法得到转子系统的不平衡响应特性。太兴宇［7］研究了透平机械中多转子系统的稳定性，又用两种方法分析了不同参数下转子系统的动力学特性。在齿轮啮合转子系统中，面齿轮传动是一种比较新颖的传动形式，面齿轮传动以其质量轻、体积小、噪声低、重合度大等优点，被广泛应用于航空航天方面，美国Apache武装直升机使用的便是含有面齿轮的传动系统。但是，关于面齿轮耦合转子系统的动力学研究相对较少，相关文献对此研究并不多见。

转子动力学的主要研究内容就是转动系统的临界转速与不平衡响应，临界转速是指转动系统发生共振的转速，而不平衡响应指的是转动系统在不平衡量、齿轮偏心、联轴器不对中等情况下，系统的振动响应。本文针对一个航空减速器中含有面齿轮传动的多转子系统进行动力学特性分析，主要是从系统的临界转速和系统不平衡响应入手进行研究。

1 齿轮耦合转子系统的动力学模型

如图1所示为用Solidworks建立的本文所分析的某航空减速器中的齿轮耦合转子系统。此传动系统中共有三根轴，分别通过一对斜齿轮啮合与面齿轮和直齿圆柱齿轮啮合联接到一起。

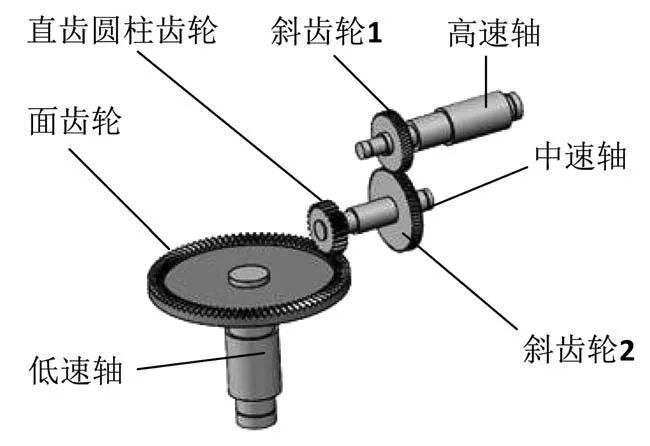
图1 某航空减速器中的三轴转子系统

1.1 面齿轮耦合转子系统的动力学模型

在本文所研究的三轴转子系统中，面齿轮传动最为关键，因此建立其动力学模型。如图2所示为面齿轮传动动力学模型。其中直齿圆柱齿轮i为主动轮，Oi、Oj分别为两轮的中心。

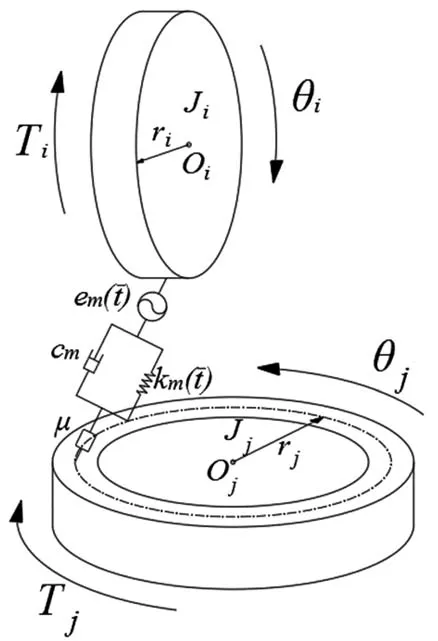
图2 面齿轮传动动力学模型

根据图2可以推导出面齿轮副的动力学模型，用微分方程可以表示为：

式中，Ji、Jj为主、从动轮的转动惯量；θi、θj为主、从动轮的扭转角位移；cm为齿轮啮合的阻尼系数；ri、rj为直齿圆柱齿轮与面齿轮的啮合基圆半径；km(ˉ)为齿轮啮合的时变啮合刚度；δ(l)为齿轮啮合的间隙非线性函数；为主、从动轮的转矩；为主、从动轮齿面摩擦转矩。

两齿轮在啮合线上的位移xi与xj分别为：

根据面齿轮的动力学方程可知，其固有频率为：

式（27）为系统的响应振幅α依赖于解谐参数 σ的隐函数方程，λ、Fm、Γah、ΓaT和 ξ分别代表面齿轮系统的摩擦系数、静态载荷、内部激励、外部激励与阻尼，根据五个参数的不同取值，可以分别绘制出不同的频响曲线，如图3所示。

图3中可以看出系统中的摩擦系数改变了系统的共振频率，但对振幅的影响小；静态载荷改变了共振频率；内、外部激励均改变了共振的振幅与发生频率；阻尼的增大对系统的振幅起到抑制作用，可以通过增大阻尼的方法，来减小面齿轮传动系统振动与噪声。

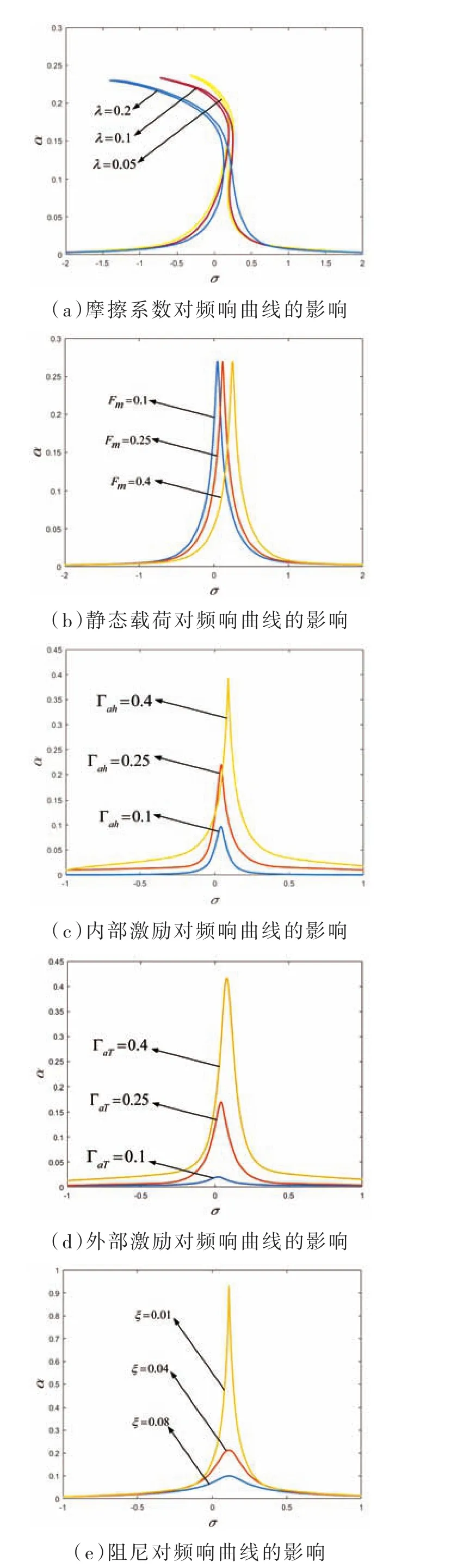
图3 内、外部激励引起的面齿轮传动系统的共振频响曲线

1.2 转子系统的有限元模型

将Solidworks建立转子系统的三维模型，保存为“.x_t”格式后导入有限元分析软件Workbench中定义材料的密度为7 500 kg/m3，弹性模量为212 000 Mpa，泊松比设置为0.31。两对齿轮之间的接触类型均设为摩擦接触，摩擦系数设置为0.1，接触刚度系数设置为1，稳定阻尼因子设置为0.02。划分网格后得到整个系统的有限元模型如图4所示。模型中包含有158 575个节点和48 295个单元。

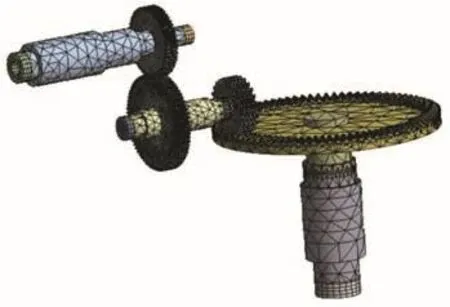
图4 齿轮耦合转子系统的有限元模型

2 转子系统的临界转速

临界转速也称为共振转速，转子在到达临界转速且该转速刚好等于该转子的某一阶模态频率时，系统发生振动，共振严重的可能会产生相当严重的后果。一般的原则是要求回转体的转速要小于一阶临界转速的20%［8］。因此，转子系统的临界转速分析在转子动力学分析中占有相当重要的地位。想要得到转子系统的临界转速先要对其进行模态分析，得到转子系统的固有频率后，根据陀螺效应对齿轮耦合转子系统的影响绘制可以得到临界转速的Campbell图。

本文先分别对高、中、低速轴单独进行模态分析，再对1.2节中所建立的系统的有限元模型进行模态分析，对比所得到的系统与三根轴的模态振型的相符之处，能够发现三根轴通过齿轮啮合耦合成为一个转子系统后，会相互作用，派生出了多阶新频率，同样，三根轴的部分固有频率会消失，由于篇幅原因，本文不一一列出单轴与系统的模态振型，只列出了经对比后，各轴与系统的固有频率比较表，如表1所示。

表1 各轴与系统的固有频率的比较表

从表1可以看出各根轴经过齿轮啮合后会派生新的频率，也会丢失原有的单根轴的固有频率，且面齿轮的固有频率对于转子系统的影响较大。得到了单根轴及其系统的固有频率便可画出对应的Campbell图，如图5-图8所示。图中所代表1x激励的粗实线与各阶频率的交点，也就是三角形交点所对应的横坐标轴的值就是转子系统的临界转速。表2为临界转速的数值。

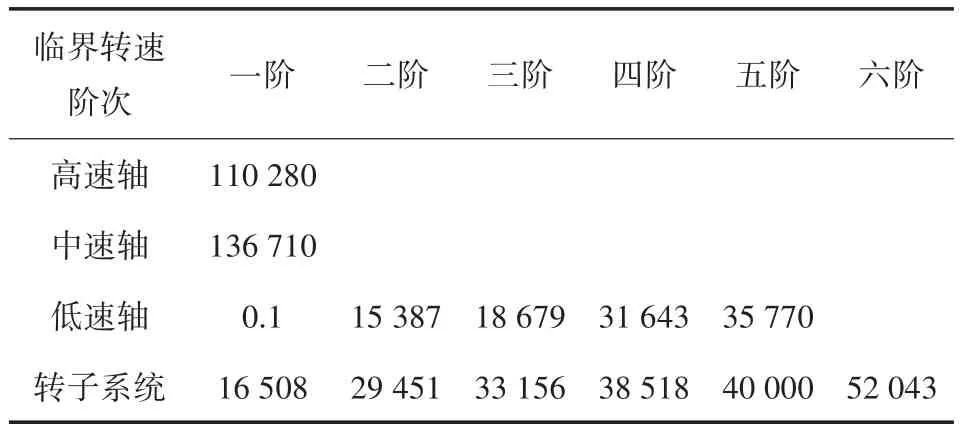
表2 单轴与系统的临界转速（单位：rpm）

从图5和图6中可以发现，高速轴与中速轴在单独旋转时，均只有一阶临界转速110 280rpm和136 710rpm，远远大于各自的额定转速，说明两个轴在单独旋转时十分稳定，不会产生共振。图7中，装配有面齿轮的低速轴则有五阶临界转速，第一阶临界转速0.1rpm是在减速器启停时产生的振动，可忽略不计。通过对比图8与图5、图6、图7可以发现，低速轴的三、四、五阶临界转速与转子系统的一、二、三阶对应，转子系统的其余临界转速皆为转子由于齿轮啮合以及转轴的弯扭耦合派生出的新的临界转速。

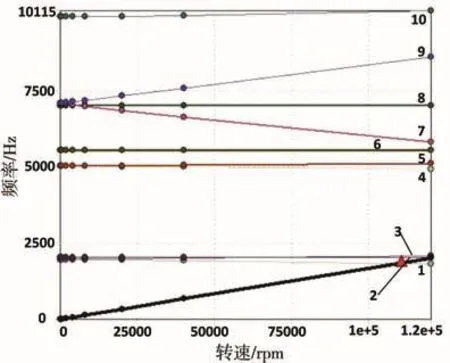
图5 高速轴的Campbell图

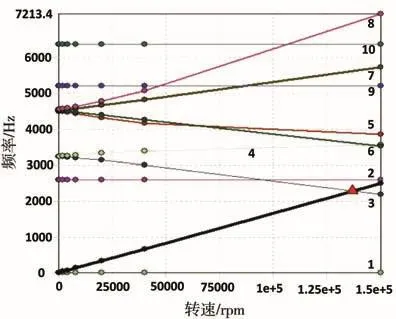
图6 中速轴的Campbell图

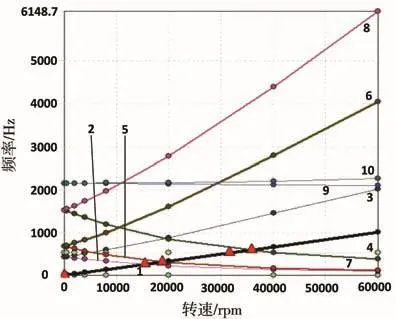
图7 低速轴的Campbell图

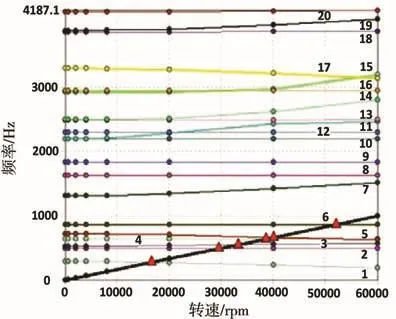
图8 转子系统的Campbell图

3 转子系统的不平衡响应

转子系统在运转时受到其质量不平衡的离心力的作用下发生的受迫振动即为转子的不平衡响应。研究转子系统的不平衡响应可以了解转子系统的振动特性，为后续转子系统的实验以及优化提供了理论参考。本文根据美国石油协会API确定了转子系统的一种工况的不平衡量以及加载位置，针对转子系统的该种工况进行不平衡响应分析。表3为该工况下不平衡量的参数。图9为该工况下转子系统不平衡载荷示意图。

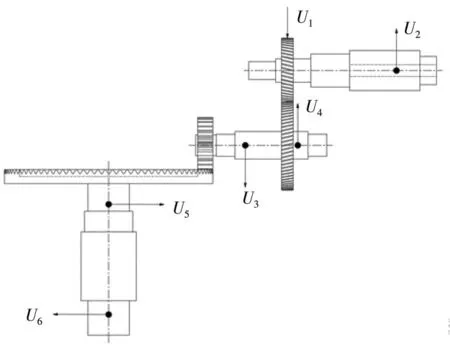
图9 转子系统的不平衡载荷示意图

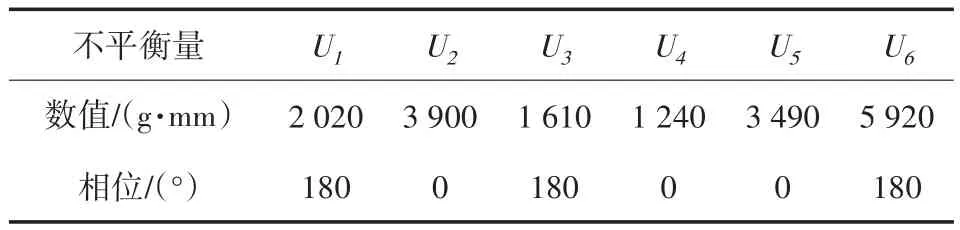
表3 不平衡量的参数

使用Workbench中的Harmonic Response和Transient Structural模块对此工况下输入转速为1 000rpm时的整个转子系统进行不平衡响应分析，得到的振幅时域和频域响应图如图10所示。其中，图10中的（b）、（d）、（f）中的五条曲线分别代表 1 000、2 000、3 000、4 000、5 000rpm 所对应的位移频域曲线。

图10中可以明显看出此系统为一个减速系统，幅值从高速轴到低速轴依次降低；从图10的（b）、（d）、（f）中可以看出，随着转速的升高，幅值也随之增大，且每个测试点的不平衡量方向上均只有一个激励频率，激励频率的数值如表4所示。根据表中数据可以发现该激励频率几乎与各齿轮所在转轴的对应转动频率相近，可知在转子系统运转时，每根转轴在其不衡量方向上仅受本身的振动激励。

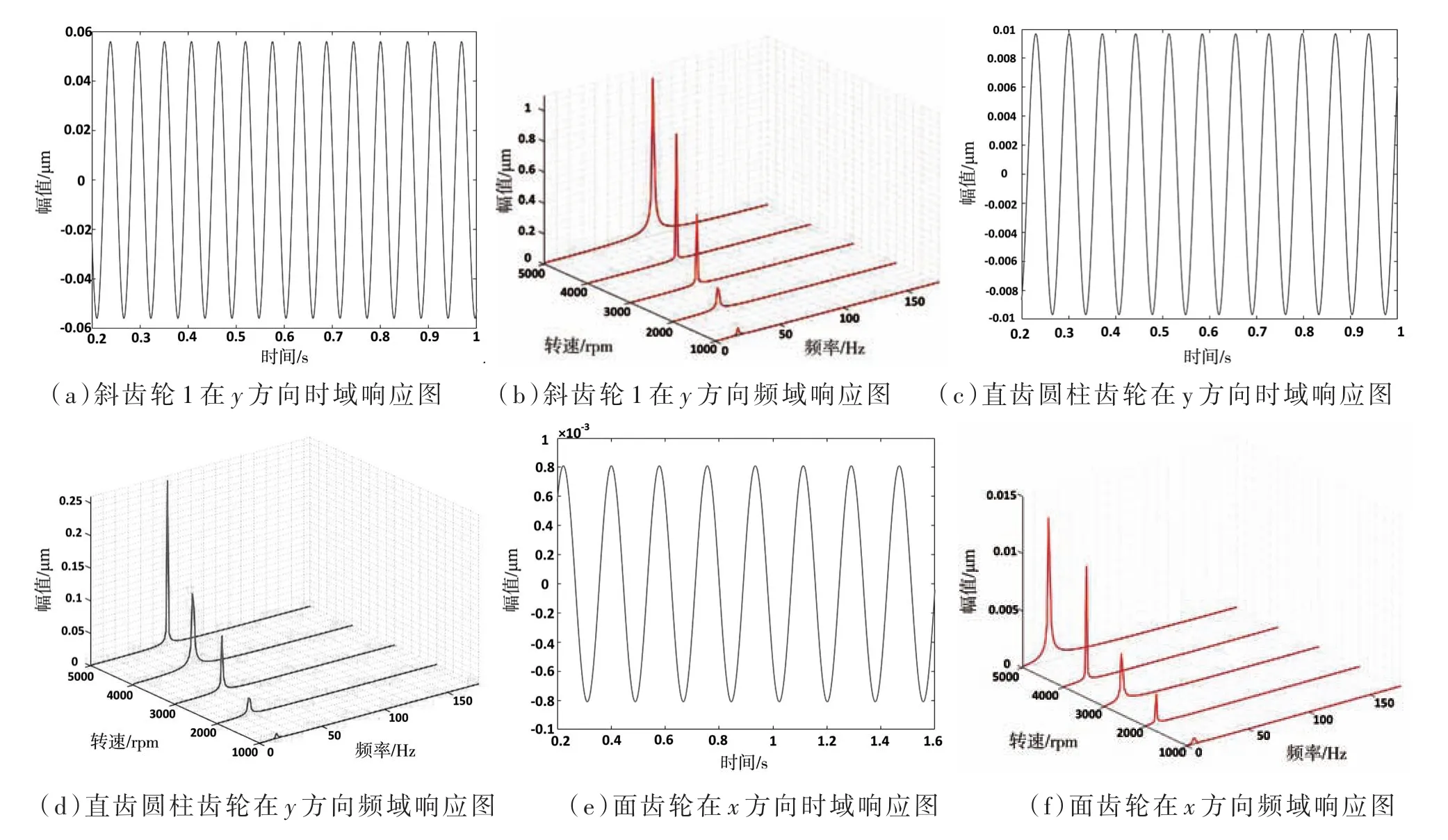
图10 转子系统各测试点位移的时域频域响应图

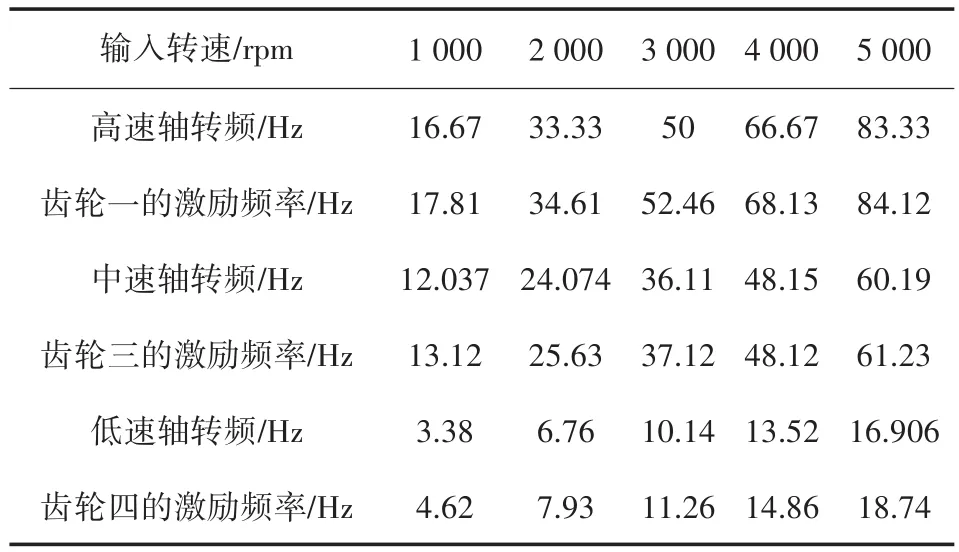
表4 不同转速下各齿轮不平衡量方向的激励频率

下面分析旋转角位移方向上系统的不平衡响应。如图11所示。其中，图11中的（b）、（d）、（f）中的五条曲线分别代表 1 000、2 000、3 000、4 000、5 000rpm所对应的角位移频域曲线。

从图11中可以发现，在各轴的转动方向上均有三个激励频率，其幅值随着转速的升高而增大，激励频率的数值如表5所示。表中可以发现在转子系统运转时，各轴在其旋转方向上会受到的激励频率分别与三根轴的旋转频率相对应，可知转子系统在运转时，每根转轴的转动角位移方向上，会受到系统中所有转轴的转频激励。

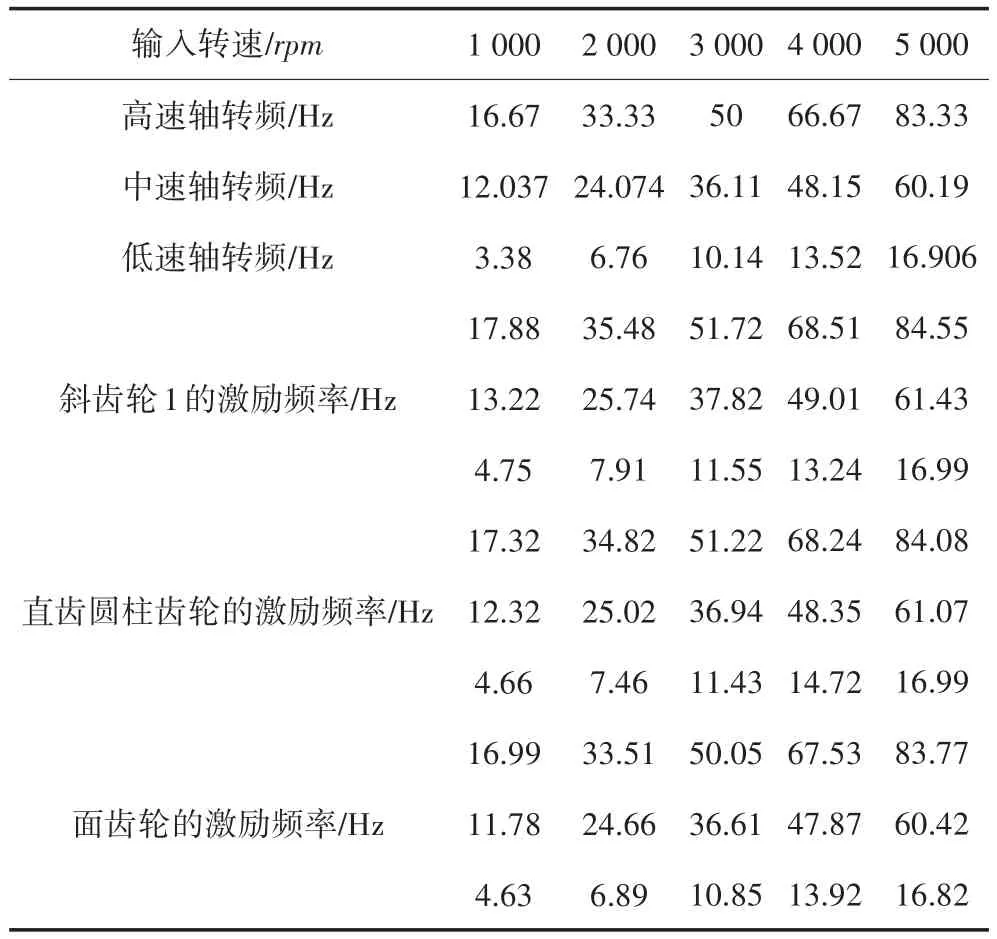
表5 各齿轮角位移方向的激励频率

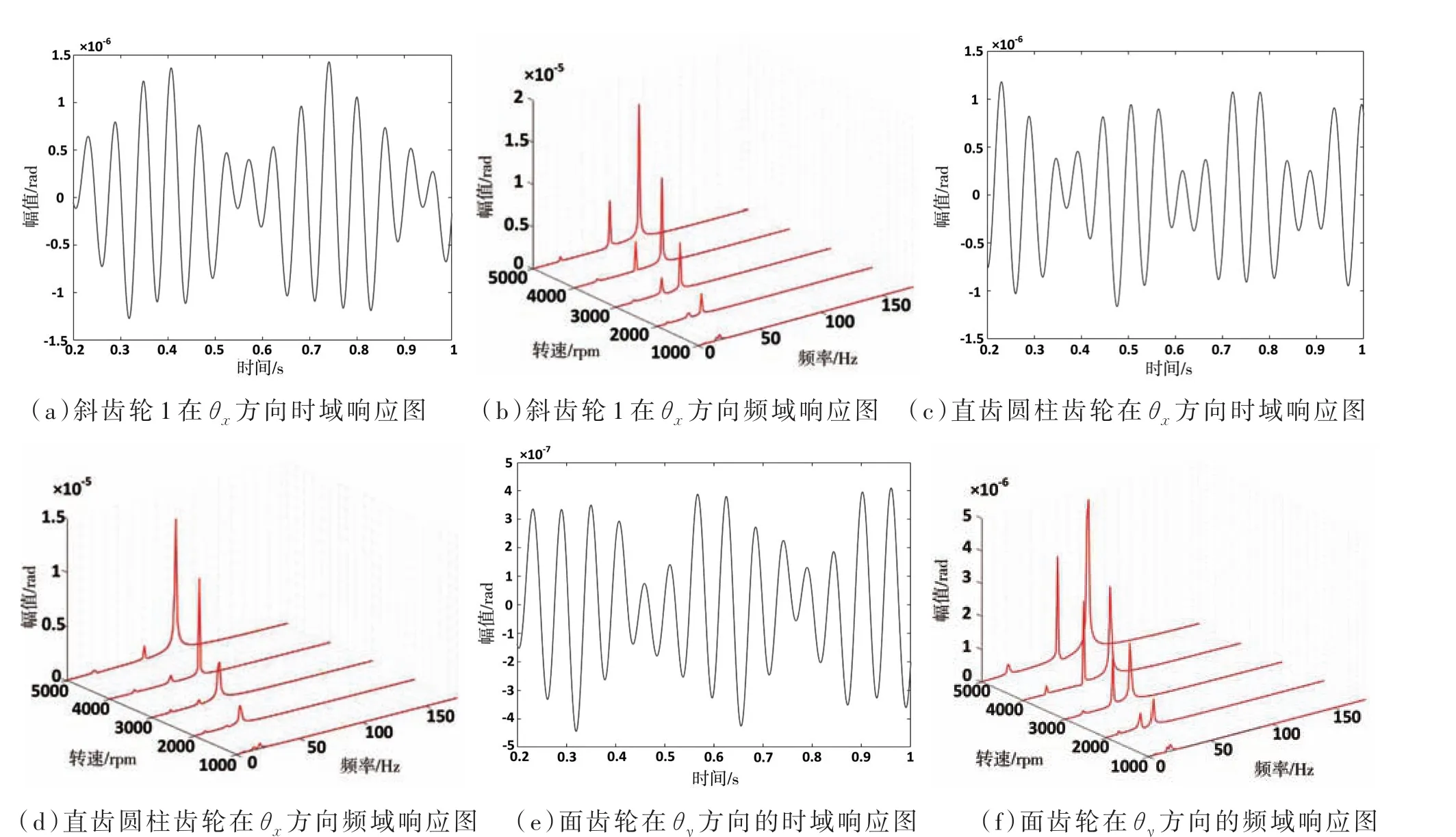
图11 转子系统各测试点旋转角位移的时域频域响应图

为了更直观的研究齿轮耦合转子系统从0增速到5 000rpm过程中转子系统的不平衡响应特性，将之前仿真得到的结果以节点的方式导入到Matlab中进行编程，得到三根转轴以及整个齿轮耦合转子系统的振幅图如图12所示。

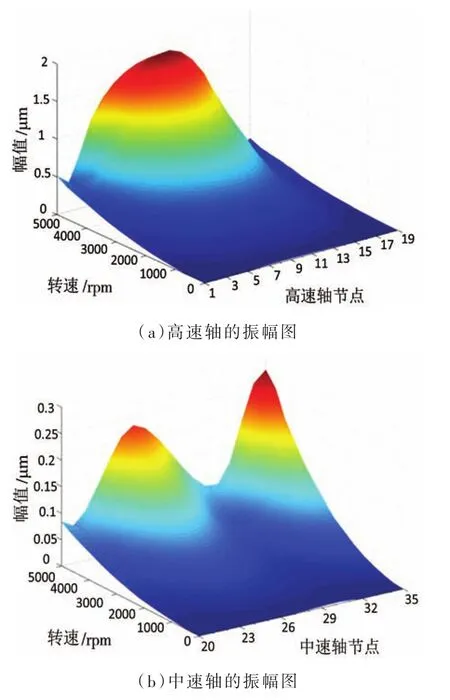
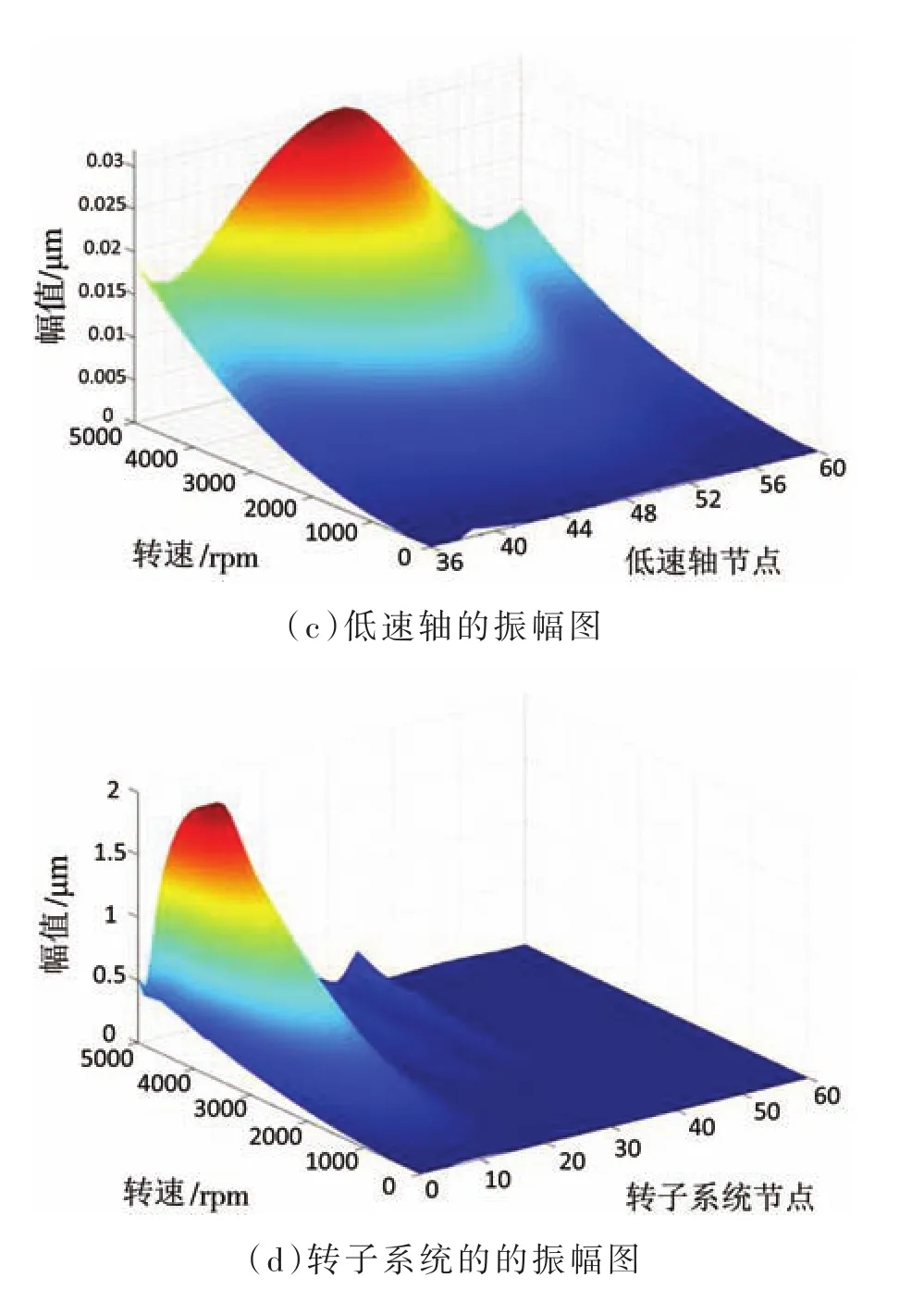
图12 各轴及转子系统的振幅图

根据图12可知，随着转速的增大，转子系统的振幅逐渐增大，高速轴的振幅最大处为其跨中位置，大小为1.77μm；中速轴的振幅最大处为装配有支持圆柱齿轮的外伸轴的端节点35，大小为0.28μm；低速轴的振幅最大处为其跨中位置，大小为0.032μm。随着振幅的增大，系统没有出现响应峰值，且振幅均小于API标准，转子系统能够安全可靠的在0～5 000rpm范围内运转。

4 结论

本文根据面齿轮的传递方式，建立了面齿轮耦合转子系统的动力学模型，将solidworks建立的三维模型导入到Workbench中进行有限元分析，分析转子系统的固有频率、临界转速与不平衡响应，根据结果得到了如下结论：

（1）齿轮耦合多转子系统的动力学特性不是各个转子特性的简单组合，而是会产生新的固有频率以及新的临界转速；且本文所研究的多轴减速器的临界转速远远大于其工作转速，说明其运转十分稳定。

（2）面齿轮传动对多轴转子系统的固有频率以及临界转速影响较大，其动力学特性对整个转子系统来说十分重要。

（3）齿轮耦合多轴系统在受到不平衡量的激励时，随着转速的升高，各测试点的振幅也随之升高。系统在运转时，其不平衡量的方向上会受到所在轴的转动频率激励；在其转动方向上会受到每根转轴的转动频率激励。

（4）在不平衡量的影响下，转子系统转动时，随着转速的升高，转轴的振幅变大，且转轴的跨中位置以及外伸轴端是转子振幅最大的位置。在转子动力学的研究中，转速对齿轮耦合多轴系统的影响十分重要。