新能源发电系统参与频率和电压响应的模型预测控制策略
2021-06-30张祥成王昭亮黄存强程文俊刘兴文
安 娟,张祥成,王昭亮,黄存强,张 娉,程文俊,刘兴文
(1.国网青海省电力公司经济技术研究院,青海省西宁市 810008;2.中国电建集团西北勘测设计研究院有限公司,陕西省西安市 710065 )
0 引言
在输电网中,有功功率与频率控制密切相关,无功功率与电压控制密切相关[1]。虽然电力系统的电压和频率通常保持在一定的范围内,但当发生扰动破坏平衡时,仍会导致频率与电压失稳。随着新能源发电在电网中的渗透率不断提高,电网单独依靠传统能源进行调频、调压的能力被逐渐削弱[2,3]。为此国家出台一系列新能源发电站接入电网的标准,要求提供频率调节,同时应增加新能源发电的无功调节能力,为电网的稳定运行提供一定的频率支撑和电压支撑[4-7]。大规模风力发电和太阳能发电通过并网变换器接入电网,具有灵活地调节有功和无功功率的潜能,应对电网频率和电压发生波动的情况及时响应[8-10]。
电池储能系统以其响应速度快、效率高等特点,已成为目前流行的一种电网级储能形式,电池储能系统具有良好的调频和调压的性能,大规模电池储能系统被广泛用于提高输电效率和电能质量[11-13]。随着成本的降低、寿命的延长以及储能相关技术的进步,在中小型电力系统中,电池储能系统具有很可观的应用前景[14-16]。
有鉴于此,考虑将风电场、光伏电站和电池储能系统相结合,发挥它们在电压与频率控制方面所具有的优势,来提高电网的频率、电压调节能力。风电场、光伏电站和电池储能系统的结合具有更大的可调度功率,在电压和频率控制方面具有协同增效的优势。然而,风电场、光伏电站和电池储能系统的结合需要可行的最优控制策略,该策略需要能分别决策出这些电源的最优功率输出。此外,要实现这些电源的可靠运行,还需要满足系统正常运行所需的约束条件。这些约束条件包括风电场的输出功率极限、光伏电站的输出功率极限、电池储能系统的充放电功率极限、电池储能系统的荷电状态(state of charge,SOC)极限,由此产生了一个在线约束最优控制问题。
根据已有的相关研究,模型预测控制(model predictive control,MPC)是解决这一约束最优控制问题的理想方法,因为它考虑了系统的约束条件,并以最优的方式解决了控制问题。为此,已经有一些文献采用MPC来解决多电源的电压或频率控制问题。在文献[17]中,作者设计了用于风电场的MPC控制器,以优化分配多个永磁同步电机之间调频功率输出。文献[18]中,针对风电场、电池储能系统和其他分布式能源的MPC被用于确保足够的调频性能,同时考虑了单个可控功率源的物理限制。在文献[19]中,风电场的各种无功补偿和电压调节装置通过MPC来协调,使所有母线的电压保持在可行的范围内。利用MPC,可以有效地解决系统电压或频率控制的多变量多目标约束优化问题。然而,在高新能源渗透率的电网中,用MPC来最优地分配各可调度功率源的输出,同时调节电网的电压和频率,目前还未见报道。
基于上述分析,考虑提出一种新的风电场、光伏电站和电池储能系统的联合控制策略。考虑使用双层MPC结构:基于MPC和滚动时域估计,上层MPC考虑下层新能源发电系统所具有的约束条件,计算出下层风电场、光伏电站和电池储能系统各子MPC的有功无功参考;下层控制器负责执行参考指令,决策出各功率变换器的开关状态,送给对应的发电系统,以在电网频率和电压波动的情况下参与电压和频率控制,提高电网调频和调压的能力。
1 系统模型
1.1 新能源发电系统结构图
研究的新能源发电系统如图1所示,包括陆上风电场、光伏电站、电池储能系统、升压变压器和双向变换器,该系统通过传输线连接到主电网。

图1 新能源并网发电系统结构图Figure 1 Structure chart of the studied new energy power generation system
1.2 系统频率动态模型
当负荷和发电量不匹配时,交流电网的频率偏离额定值。为建立预测模型,考虑含风电场、光伏电站和电池储能系统的电网频率动态模型[20-22]。

式中:f是实际的电网频率;PG是所有常规机组的总有功功率输出;PL是负荷功率;PW是风电场有功功率输出;PB是电池储能系统的有功功率输出;PP是光伏电站有功功率输出;H是电网惯性时间常数;fn是电网额定频率;PLN是在额定电网频率下的电网负荷需求;Df是负荷调节系数。
1.3 系统电压动态模型
根据泰勒近似,在系统某一节点R,工作点电压vR与有功、无功功率注入的关系可以写成[18]
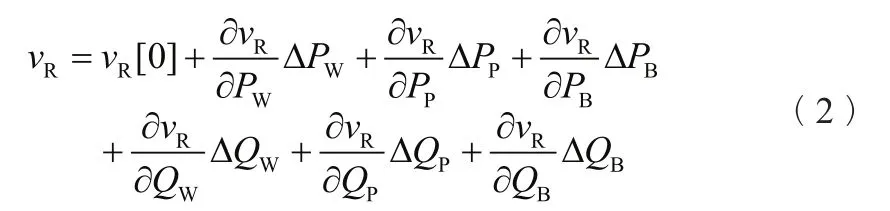
式中:vR[0]表示初始电压,ΔPW、ΔPP、ΔPB、ΔQW、ΔQP和ΔQB表示有功 /无功注入的变化 ;∂vR/∂PW、∂vR/∂PP、∂vR/∂PB、∂vR/∂QW、∂vR/∂QP和 ∂vR/∂QB是电压相对于功率的变化率,通过对这些变化率的计算,建立了电压预测的线性化模型。这些变化率的典型计算方法是,通过实时求解潮流问题导出雅可比矩阵而得到。
1.4 储能能量平衡方程
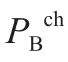

式中:EB即为电池储能系统SOC,表示电池储能系统剩余容量与完全充电状态的容量的比值,常用百分数表示;ηch代表电池储能系统的充电效率;ηdis代表电池储能系统的放电效率;ΔTB是MW到MWh的转换常数。
2 预测控制策略设计
2.1 控制策略设计原则
本文的新能源发电系统参与频率与电压响应的MPC策略中,预测控制器的总体目标为:在满足风电场、光伏电站、电池储能系统等被控对象的各自约束条件的前提下,寻找最优的控制输入使得电网频率和电压各自的预测轨迹与参考轨迹尽可能接近,同时控制代价要尽可能小。为了实现上述目标,关键问题是在频率和电压发生波动时,最优地决策出这些可调度电源的有功和无功输出指令,同时各可调度电源按照指令输出对应的有功和无功功率。因此,预测控制器的控制目标可分为两个部分:首先,考虑各可调度电源的约束条件,决策出各电源的最优功率参考;其次,控制各个可调度电源,执行相应的功率参考。为了实现这两个目标,设计了两层MPC控制策略,控制系统结构如图2所示。

图2 预测控制系统结构图Figure 2 Block diagram of the proposed predictive control scheme
在该策略中,基于实时电网电压和频率测量、功率不平衡量估计和灵敏度计算,上层MPC控制器(即f-v-MPC)计算风电场、光伏电站和电池储能系统的最优功率参考指令PB,ref、QB,ref、PW,ref、QW,ref、PP,ref和QP,ref,以满足最优的调频和调压效果。下层MPC控制结构中,储能双向变换器的子预测控制器BESS-MPC、风电场的子预测控制器GSC-MPC和MSC-MPC、光伏电站的并网变换器PV-MPC执行上层的功率参考,向电网输出对应的功率。
2.2 上层预测控制策略设计
上层f-v-MPC的目标是从风电场、光伏电站和电池储能系统的整体角度计算最优参考功率。为了获得最优的电压和频率响应,本文在MPC框架下设计了控制器。在MPC的控制框架中,必须指定一个内部离散时间预测模型来预测被控制变量的未来行为。对于上层f-v-MPC控制器,需要控制的变量是电网的频率和某些节点的电压。鉴于此,离散时间预测模型可通过系统电压和系统电压动态模型(1)和(2)得到。在该动态模型中,PG和PL都不能直接测量。因此,为了方便起见,将它们合并为一项:

从风电场、光伏电站和电池储能系统整体来看,PD可以看作是电网的总有功功率不平衡量。为了得到系统电压和频率离散时间系统动态模型,采用零阶保持离散化方法。注意式(2)是增量形式,为了便于推导,将式(1)也改写为增量形式。电池储能系统的输出功率能减小频率和电压的波动,但为了避免电池储能系统过度充电、放电,还应控制电池储能系统的SOC。因此在采样时刻k,系统整体动态方程可由式(5)表示


其中:Ts是采样周期,Δ表示状态变量在当前采样时刻和上一采样时刻的差。该模型作为f-v-MPC的预测模型,决策变量为Δf和 Δv,控制输入为 ΔPW、ΔPP、ΔPB、ΔQW、ΔQP和 ΔQB。
为了计算最优控制输入,需推导出代价函数。根据预测控制策略的总体目标,f-v-MPC的首要目标是尽可能地抑制频率和电压的波动。然而,控制性能的改善通常是以更大的控制动作为代价。就所研究的系统而言,这意味着更大幅的有功/无功功率变化、更深的充放电深度。因此,应该在控制性能好坏和控制动作幅度之间做出较好的折中。根据这个原则,f-v-MPC的优化目标函数可以写成:

其中(k+h|k)表示在k时刻,对k+h时刻参数的估计值;下标T表示上层控制器;HT表示上层控制器的预测和控制时域。αT和βT是上述两个惩罚项之间的加权向量。
此外,代价函数(6)的最小化必须满足一系列约束条件,包括风电场的输出功率极限、光伏电站的输出功率极限、电池储能系统的充放电功率极限、电池储能系统的SOC极限,同样地,这些约束采用了增量形式。
风电约束:风电场可通过转子超速和变桨距等方法预留备用容量[24],而备用容量有限,因此本文设置风电场约束如式(7)所示:
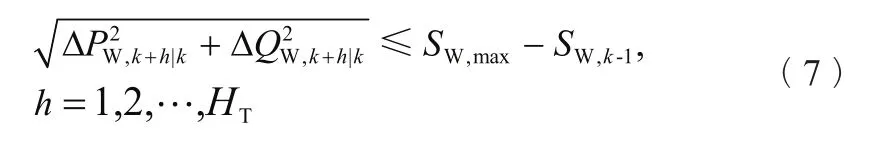
其中SW,max由风电场备用容量的大小决定。
光伏约束:由于光伏备用容量有限,因此设置光伏约束如式(8)所示:
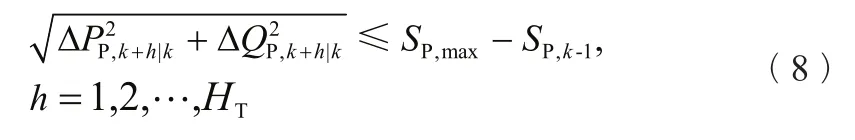
其中SP,max由光伏电站备用容量的大小决定。
SOC约束:过度放电可能会损害电池储能系统的循环寿命。同时,过度充放电使电池储能系统失去了抑制频率和电压波动的功能[25]。有鉴于此,为了保护电池储能系统,施加了以下约束:

电池储能系统功率约束:为了保护电池储能系统在充放电过程中不受损坏,应限制电池储能系统的最大充放电功率:

避免同时充放电:电池储能系统同时充电和放电是不现实的。为避免同时充放电,应满足以下约束条件:
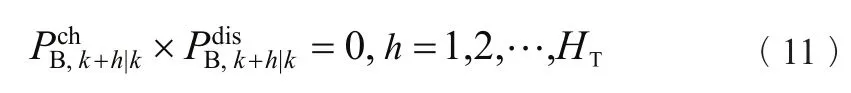
目标函数(6)与约束条件(7)~(11)共同构成以下的约束优化问题:

注意到存在非线性等式约束,即式(11),导致该问题不易求解。根据文献[23]和[26],该约束可以安全地移除,同时不影响求解结果。求解该问题,可得k时刻的最优控制输入向量,该向量的第一个元素即为当前时刻风电场、光伏电站和电池储能系统的输出功率应变化的量,这些功率变化量将输出给下层控制器。
2.3 有功功率不平衡量估计
为了解决(12)中的f-v-MPC问题,需要系统有功功率不平衡量PUB。从新能源发电系统的角度来看,PUB不能直接测量。为了解决这个问题,因此本文设计了MHE估计器来估计PUB。
与MPC相同,MHE也是基于系统动态模型而设计的。为了解决估计问题,将系统频率动态模型(1)改写为:
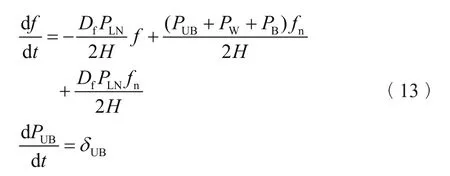
该模型可以进一步离散为:


2.4 下层本地预测控制策略设计
在下层控制层,有四种MPC控制器。如图2所示,这些控制器包括储能双向变换器的子预测控制器BESS-MPC、风电场的子预测控制器GSC-MPC和MSC-MPC、光伏电站的并网变换器PV-MPC,据作者所知,已有大量关于功率变换器的MPC的研究[27]。关于WF背靠背变换器有功和无功控制的MPC策略,感兴趣的读者可参考文献[17]、[28]和[29];适用于光伏逆变器和电池储能系统双向变换器的MPC控制,感兴趣的读者可参考文献[30]、[31]和[32]。本文的下层控制器均使用有限集(finite control set,FCS)模型预测控制,以下层储能预测控制器BESS-MPC的有功功率控制为例,从图3的局部放大图可以看出,实际输出功率能快速跟踪参考指令,且无超调,该本地控制方法具有良好的动态功率跟踪性能。

图3 下层电池储能系统对上层功率参考指令的跟踪Figure 3 Response to step change in the active power reference of bottom-layer battery energy storage system
3 仿真研究
3.1 仿真模型
为验证所提出的电压和频率控制策略的有效性,对含新能源发电系统的电网进行了仿真研究。仿真中使用图4所示的电力系统。为了更好地模拟实际电网中频率和电压的变化过程,同时实现仿真速度与精度的平衡,分别用三台典型同步发电机和一台典型永磁同步发电机对电网常规发电机和风电场进行建模。因此,仿真系统主要包括三个常规发电机,永磁同步发电机,光伏电站,电池储能系统,变压器,输电线路等。风电场、光伏电站通过两级升压连接到公网。

图4 电网仿真结构图Figure 4 Power system model used in the simulation studies
仿真中电网包括3台额定值为440MVA、500MVA和240MVA的常规同步发电机,并预留了调频备用容量。原始负荷水平为869.6MW。风电场额定容量为60MVA,光伏电站额定容量为40MVA,风电场与光伏电站的备用容量均设置为15%。电池储能系统容量为15MVA,电池储能系统充放电效率η设置为90%,SOC上下限设置为80%和20%。
为了模拟频率和电压波动,在t=10s时负荷骤降40MW,同时消耗的无功功率减少15Mvar。电网初始频率值为50Hz,调频死区设置为20mHz。
3.2 仿真结果
图5显示了不同控制策略下新能源发电系统参与调频时,电网的频率变化。通过对比可以看出,在风电场、光伏电站和电池储能系统减小有功出力之后,频率波动的峰值从50.43Hz降低到50.24Hz,系统频率恢复到调频死区的时间为t=28.43s,而无新能源发电系统参与频率控制时,频率恢复到调频死区的时间为t=36.31s,电网的调频性能得到了较大改善。

图5 本控制策略下的系统频率特性Figure 5 System frequency characteristics with proposed control strategy
图6给出本控制策略下,电网电压的动态变化曲线。可以看出,在新能源发电系统吸收无功时,暂态电压得到了改善,电压峰值从1.130p.u.降低到1.075p.u.;同时母线电压最终稳定在1.000p.u.,而没有新能源发电系统参与电压调节时,母线电压最终稳定在1.039p.u.。因此通过以上观察,可认为本控制策略较好地改善了峰值电压和稳态电压。

图6 本控制策略下的系统电压特性Figure 6 System voltage characteristics with proposed control strategy
图7和图8给出了所有新能源发电系统的有功和无功功率变化,显示了频率和电压动态特性得到改善的原因。可以看出,频率和电压发生波动时,各新能源发电系统最优地消纳电网的有功和无功。图中功率参考值均由上层f-v-MPC优化计算,并由下层风电场、光伏电站和电池储能系统本地控制器执行。图7显示了风电场、光伏电站和电池储能系统的有功功率输出,有功功率输出都较快地达到了有功功率约束的下限,这是因为在代价函数(6)中加权向量αT中使用了较大的数,而在加权向量βT中设置了较小的数,首要的控制目标是调频调压,而限制控制动作(即各输出功率变化量)为次要的,因而控制动作幅度较大。同时,注意到在上层f-v-MPC中使用增量形式的系统模型,根据控制逻辑,只有当发生欠频事件时,上层预测控制器才会令有功功率回升。

图7 各新能源发电系统的有功出力Figure 7 Active power support of each dispatchable resource

图8 各新能源发电系统的无功出力Figure 8 Reactive power support of each dispatchable resource
图8显示了电压波动期间,无功功率输出的结果。可以看出,风电场、光伏电站和电池储能系统各自响应电压波动,且都达到并没有超过无功功率下限。这些下限是在上层f-v-MPC的无功功率约束中设置的,以防无功功率过低。风电场、光伏电站和电池储能系统之间的无功功率大小由加权向量βT中的元素决定,这些元素可根据调频、调压备用容量大小来设置。
此外,从图7和图8可以看出,有功和无功均曾到达约束下限。图7中各新能源发电系统的无功在电压发生波动的初期(11s附近)到达功率下限,而后电压逐渐回升,直至电压完全恢复稳态。可以看出,本文提出的预测控制策略能最优地将功率出力限制在约束条件之内,保证系统的稳定运行。
4 结束语
提出了一种基于MPC的新能源发电参与电网电压和频率调节的控制策略,利用MPC协调风电场、光伏电站和储能等新能源发电系统的功率出力,实现了每个新能源发电系统的最优有功和无功功率输出。该策略在已有研究的基础上,达到了同时动态优化频率和电压的目的,并保证了风、光、储各自出力的最优。仿真结果表明,该策略能有效抑制电网频率和电压的波动,保证系统的稳定运行。由于本文对风电场、光伏电站、电池储能系统的模型进行了简化,下一步研究可集中在上层功率参考指令如何在各新能源发电系统内部,即单个风机、光伏板等单元之间最优分配;另外目标函数中可加入经济指标,以实现综合效益的最优化。
