拉伸试验方法A2的横梁位移速率补偿方法
2021-06-30高怡斐王春华梁新帮
高怡斐, 王春华, 梁新帮
(钢研纳克检测技术股份有限公司, 北京 100081)
ISO 6892-1:2019(E)UniaxialTestingTechnicalCommittee.MetallicMaterials-TensileTesting—Part1:MethodofTestatRoomTemperature规定的方法A2,是横梁位移速率控制,试样的实际应变速率处于一种开环控制状态,并不是像方法A1那样的闭环控制状态。试样的应变速率受到系统的柔度变形影响,其变形越大,受影响也越大,这是方法A2的主要缺点。此外,按照方法A2,横梁位移速率一旦给定,在整个试验中是定数。因此,在拉伸试验的初始阶段,横梁位移的相当部分被用于消除试样链系统各连接件之间的间隙,造成整个试验总时间大大增加、试验效率低的缺点。方法A2也有其优点,相对方法A1而言,方法A2的试验操作相对简单,所以试验室一般都乐于使用方法A2进行拉伸试验。
能否找到一种改良的方法改善前述的缺点和在一定条件下使用?笔者将探讨这个问题解决的可能性。
1 横梁位移速率补偿方法之一“斜率补偿法”
1.1 拉伸试验模型
对金属材料进行拉伸试验,其实是试样在拉伸试验系统中被拉伸的试验。所谓拉伸系统是指能够沿试样纵轴对试样链施加拉伸力的系统,试样链由试验机夹头、试样、拉杆、力传感器等串联组成,试样仅仅是构成试样链的一环。由于拉伸系统自身的变形特性,试验机的横梁位移并不是全部转移到试样产生变形,而是有部分被转移到试验机构件自身产生变形。基于这种认识,把试样在拉伸系统中进行的拉伸试验,看成为代表试验机的一个大弹簧串联一个试样的拉伸试验,如图1所示[2]。显然,在拉伸过程中,试验机横梁位移被分配到了弹簧和试样的变形上去。为了便于分析,建立一种拉伸试验模型[2]:把试样平行长度的变形作为一个变形分系统,简称平行长度系统;把试样的两过渡弧和两被夹持头部与大弹簧串联,组成另一个变形分系统,简称试验机系统,两个分系统串联成拉伸试验模型,如图2所示。根据这一模型,试验机横梁位移由试验机系统伸长分量和平行长度系统伸长分量组成,其数学模型为[2]

图1 代表试验机的弹簧串联拉伸试样的示意图Fig.1 Schematic diagram of spring series tensile specimen representing testing machine
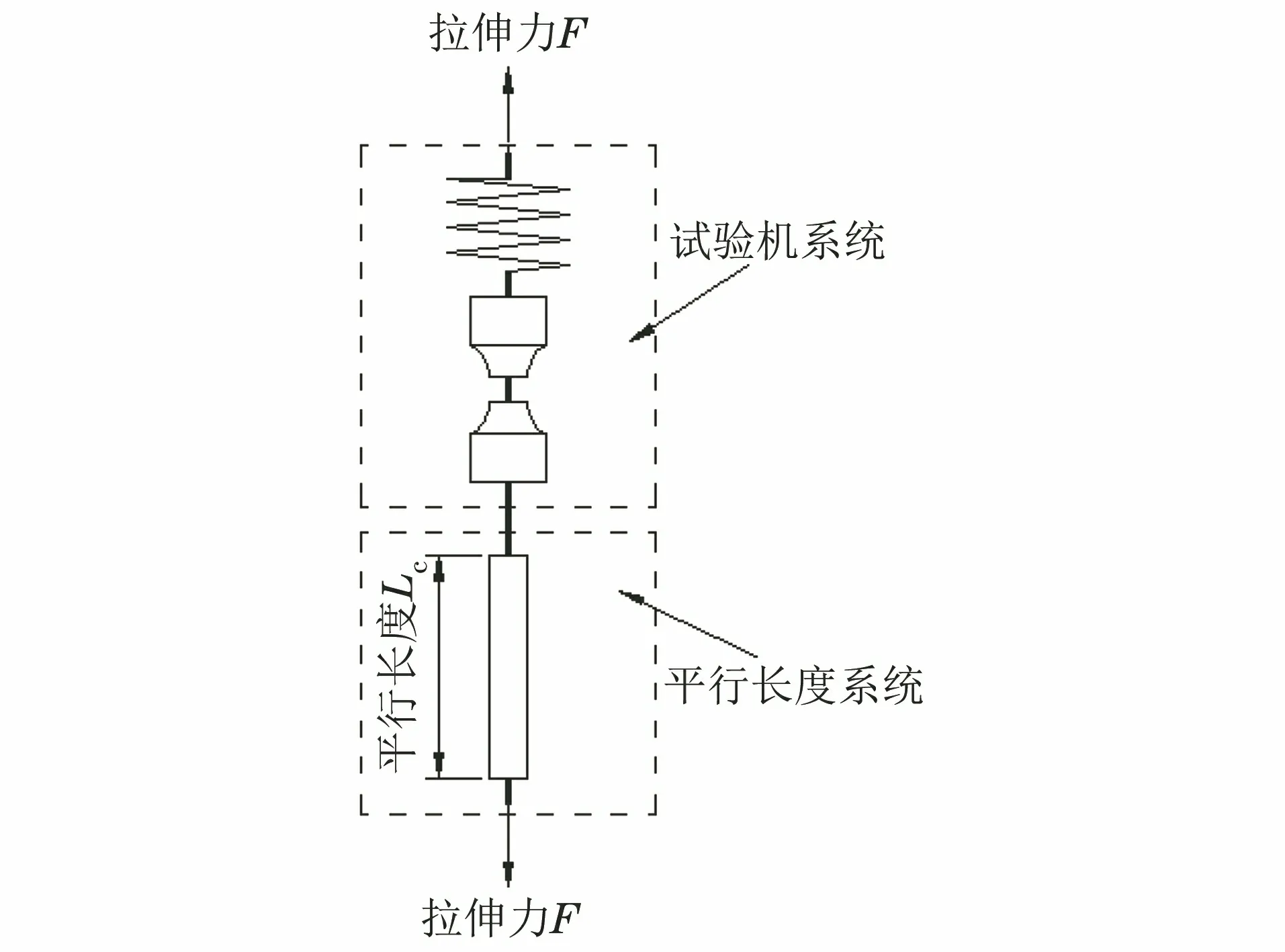
图2 平行长度系统与试验机系统串联的拉伸试验模型Fig.2 Tensile test model of parallel length system and testing machine system in series
δc=δM+δp
(1)
式中:δc为试验机横梁位移;δM为试验机系统的伸长;δp为试样平行长度(系统)的伸长。
无论试验机系统和平行长度系统分别处于弹性或塑性变形状态,式(1)表示的关系仍然保持。式(1)右边第2项伸长δp,无论在弹性或者在塑性状态,都可以表示为
δp=ΔL=epLc
(2)
式中:ep为平行长度的拉伸应变(通过引伸计系统测定);Lc为平行长度。
式(1)右边第1项伸长δM可以表示为

(3)
式中:F为施加的拉伸力;CM为试验机系统的刚度。
刚度表示给定工件或结构件在力作用下变形的困难程度,用力与变形之比表示。试验机系统的刚度CM表示为

(4)
1.2 试验机横梁位移速率和应变速率的一般性表示
为了得到试验机横梁位移速率vc的表示式,将式(1)两边取对时间的导数:

(5)
将式(2)和式(3)代入式(5)后变为

(6)
式(6)的右边的各量,其中力F和应变ep与时间有关,是时间的函数;平行长度Lc与时间无关,是常量;刚度CM在线性(比如线弹性)变形状态与时间无关,是常量,而在非线性(比如弹-塑性)变形状态与时间有关,是时间的函数。为了一般化,将刚度CM看作为变量,是时间的函数。经过推导和运算得到式(7)。

(7)
式中:M为dF/dδM,是试验机系统力-伸长曲线上对应于平行长度系统应力-应变曲线上感兴趣点m处的曲线斜率,参见图3。
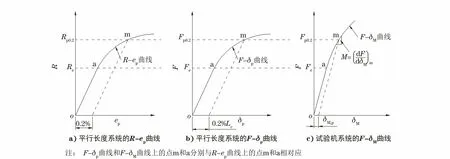
图3 平行长度系统和试验机系统的应力-应变曲线和力-伸长曲线Fig.3 Stress-strain curves and force-extension curves of parallel length system and testing machine system: a) R-ep curve of parallel length system; b) F-δp curve of parallel length system; c) F-δM curve of testing machine system
因为平行长度系统与试验机系统是串联拉伸,平行长度横截面上承受的力也就是试验机系统所承受的力,因此式(7)右边的力的速率可以表示为

(8)
将式(8)代入式(7)后,可表示为

(9)

(10)
将式(10)代入式(9),得到横梁位移速率表示式:

(11)
式(11)即为考虑了试验机系统刚度时导出的横梁位移速率一般性表示式(参见文献[2])。
根据式(11),可以建立两种不同横梁位移速率vc1和vc2之间的相互关系:

(12)

(13)
令上述两式相除,产生:

(14)
根据下面章节3的试验数据和分析结论,可以假设式(14)右边参数m1/M1≅m2/M2。这样由式(14)得到:

(15)
式(15)为方法A2中两种不同横梁位移速率的关系式。
1.3 方法A2补偿横梁位移速率的计算

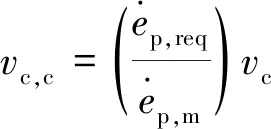
(16)
式(16)便是补偿横梁位移速率表示式。



图4 从平行长度系统的ep-t曲线测定感兴趣点(m点)处的 应变速率Fig.4 Determine the strain rate the interested point (m point) from ep-t curve of the parallel length system

(17)

2 横梁位移速率补偿方法之二“K值补偿方法”
2.1 横梁位移速率分析
根据图2所示模型,总横梁位移δc是由试验机系统伸长分量δM和平行长度系统伸长分量δp组成,其数学模型见式(1)。为了得到“平行长度估计的总应变”,式(1)两边除以平行长度Lc:

(18)
对于上式的各项,可以分别写成为
式左边项δc/Lc=eLc,是“平行长度估计”的总应变。
式右边第1项δM/Lc=eM,是“平行长度估计”的试验机系统应变。
式右边第2项δp/Lc=ep,是试样平行长度范围内的实际应变。
于是式(18)变为
eLc=eM+ep
(19)
因为上式各量都与横梁位移速率有关,是时间的函数,可以通过对上式两边取对时间的导数:

(20)
简化表示为

(21)

2.2 横梁位移速率补偿方法
使用方法A2进行拉伸试验时,由于试验机系统也产生变形,横梁位移速率vc并不全部转移成平行长度系统的伸长速率,总有部分被分流成为试验机系统的伸长速率。为了补偿被分流了的这部分横梁位移速率,需要寻找出横梁位移速率的补偿方法,下面考虑这一问题。
设想用式(22)给定的已知横梁位移速率vc拉伸整个试样链系统。

(22)


(23)
再利用式(21),上式可表示为

(24)

现在设:

(25)
于是式(24)表示为

(26)
式(26)为横梁位移速率的一般性表达式,式中符号下标字母m表示该符号代表的量与感兴趣点m相关。
对于同一感兴趣点m,两种横梁位移速率vc1和vc2,可以分别写出表示式:

(27)

(28)
两式相除,得到:

(29)
根据下面章节3的试验数据和分析结论,可以假设上式右边参数K1≅K2,这样式(29)可以表示为

(30)

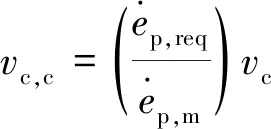
(31)
将式(22)代入上式得到:

(32)

从式(31)和式(16)可以见到,两式相同,这表明:“斜率补偿”方法和“K值补偿”方法分别得到的补偿横梁位移速率表达式(32)和式(16)两者等效。
3 支持假设参数K1≅K2和m1/M1≅m2/M2的试验数据和分析
文献[3]的表2给出了关于Rp0.2感兴趣点的比值Ky和在弹性阶段的80%Rp0.2处感兴趣点的比值Ke的测定结果,摘录于表1。试验用钛合金试样(Rp0.2=977 MPa,E=120 GPa)。
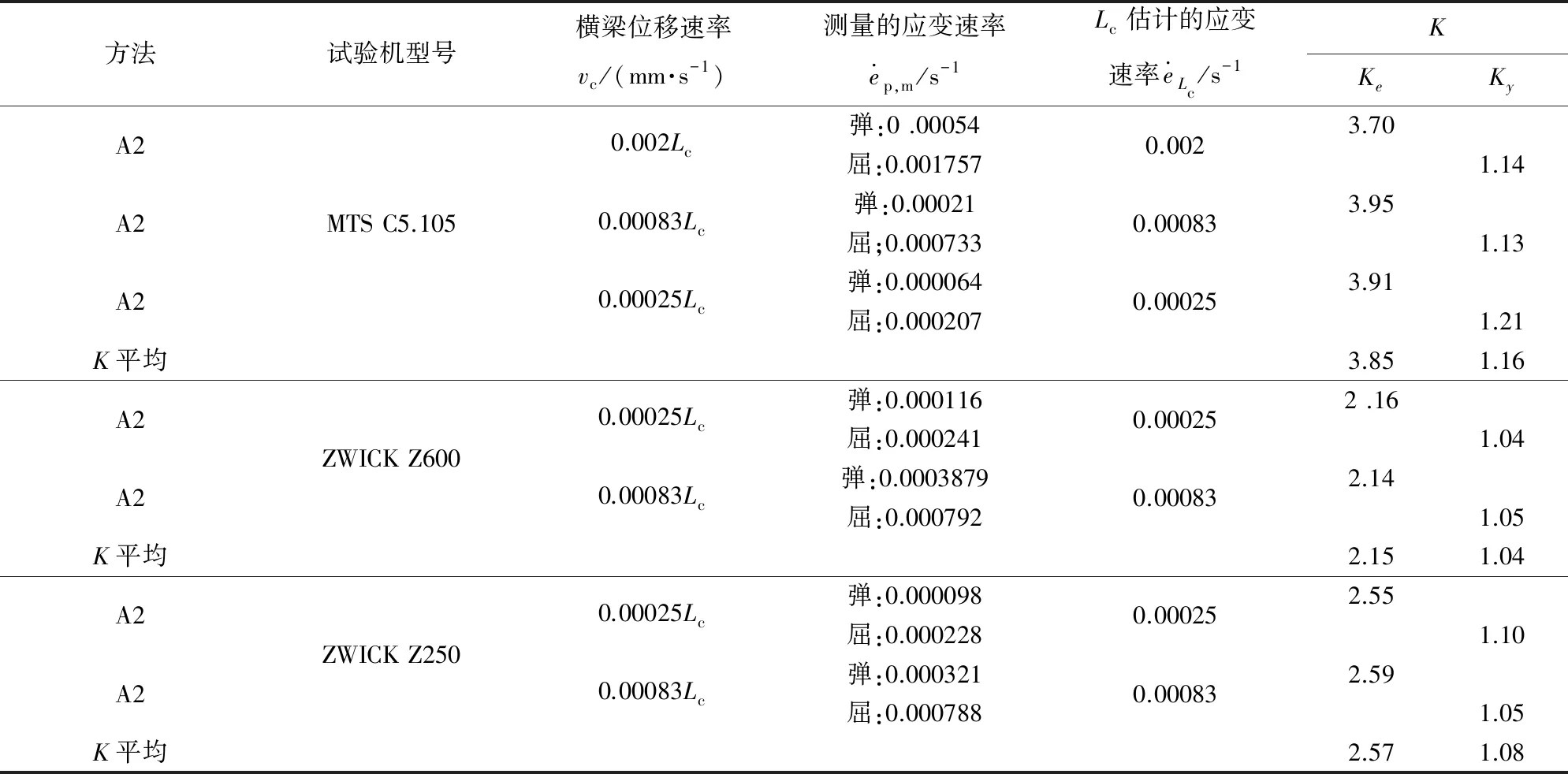
表1 横梁位移速率vc与K值试验数据Tab.1 Crosshead displacement rate vc and K value test data
从K值测量结果来看,对于同一试验设备,相同试样,相同感兴趣点(即同一性能点)情况,K值测量结果的分散性见表2。
从表2的分散性来看,相同试样和相同试验设备采用不同的横梁位移速率的试验,对于相同感兴趣点的比值K其值分散性在4%以内,差别并不大(无本质上的差别),而横梁位移速率试验范围从0.00025Lc至0.002Lc相差8倍。据此可以认为,对于相同感兴趣点,K值基本不随横梁位移速率的变化而变化,是近似恒定值[3]。这结论有力支持了参数K1≅K2和m1/M1≅m2/M2的假设,进一步分析如下。

表2 K值的分散性(相对标准偏差)Tab.2 Dispersion of K value (relative standard deviation) %
根据前面关于横梁位移速率vc一般性表示的式(11)和式(26),可以写出:
(33)

(34)
便有:

(35)

(36)
两式相除并化简

(37)
根据表2试验数据分析得出的结论,相同感兴趣点的比值K其值近似一致相同。则有:
K1≅K2
(38)
因此,式(37)变为

(39)
于是得到:

(40)
应用式(40)和(38),可以分别得到补偿横梁位移速率vc,c表示式,见式(16)和式(31)。
4 讨论
4.1 K值的变化趋向和取值范围
采用方法A2进行的拉伸试验,试验初始阶段中K值处于较高的值,随着试验进行其值逐渐降低,如果呈现平台屈服,其值接近1,如果呈现连续屈服,例如在屈服强度Rp0.2附近其值呈现大于1。试验最初始阶段K值较高,是因为此阶段横梁位移较大部分用于消除试样链连接件之间的间隙,造成平行长度的应变速率与目标应变速率相差较大。进入屈服阶段K值较低,甚至接近1,是因为进入屈服阶段,力的增加速率比弹性直线阶段的低,试验机系统的应变速率分量增速相对降低,而平行长度的应变速率分量增速相对较快,而且逐渐接近目标应变速率。

4.2 K值补偿应用于弹性阶段以缩短试验总耗时
当感兴趣点是在弹性阶段,K的值一般都比屈服阶段的高许多,所以对于该点的横梁位移速率补偿也高许多。这意味着在该点之前的试验耗时将缩短许多。如果为了缩短试验耗时为目的,建议预备试验时测量K值的点选在材料屈服强度Rp0.2的80%附近处,以便有足够区间能将横梁位移速率平滑转换至屈服阶段所需的横梁位移速率。
4.3 K值补偿方法和斜率补偿方法的优缺点
缺点:两种方法都必须事前做预备试验,在感兴趣点测定K的值以便用于计算补偿横梁位移速率。也就是说,一批相同的试样,第1根试样必须用于预备试验,以获得补偿横梁位移速率数据用于同批其余试样的试验。必须保持试样和试验设备相同,两者或其中之一改变需重新做预备试验。
优点:①同批其余试样使用补偿横梁位移进行方法A2试验,对于感兴趣点能起到改善应变速率的效果,即改善试样平行长度的应变速率与要求的应变速率的接近度。②缩短试验总耗时,提高试验效率,对于大生产的大批量试样的试验更有意义。
4.4 国际标准ISO 6892-1:2019附录F的修订建议
4.4.1 式(F.1)、式(F.2)和式(F.3)中的刚度CM修改为斜率M


只有根据上述的横梁位移速率通式,才能得到补偿横梁位移速率公式(见1.2和1.3)。
4.4.2 删去式(F.1)和式(F.3)
计算补偿横梁位移速率时,并不需要式(F.1)和式(F.3),完全可以将其删去。
4.4.3 给出补偿横梁位移速率vc,c的公式
给出补偿横梁位移速率vc,c的公式:
或者,当在预备试验中已测定和计算出了K的值时:

5 结论
(1) 根据建立的拉伸力学模型,导出了当考虑试验机系统柔度(刚度的倒数,并将其看成为时间函数的变量)时的补偿横梁位移速率表达式,和考虑试验机系统伸长时的补偿横梁位移速率表达式,两公式完全等效。适用于国际标准ISO 6892-1:2019的附录F对于方法A2的补充。
(2) 国际标准ISO 6892-1:2019的附录F需要做修改,见4.4章节。
(3)K值补偿方法对于连续屈服状态的试样,使用补偿横梁位移速率能获得改善应变速率的效果。当用于弹性阶段能缩短试验总耗时间,提高试验效率,尤其适用于大批量相同试样的试验。
(4) 提出的两种补偿横梁位移速率方法,主要适用于相同试样(试样的几何形状,尺寸和材质相同)和相同试验设备下采用方法A2的重复试验,同批相同试样第一根试样必须用于预备试验,以获得相关参数用于计算补偿横梁位移速率。
