基于VG-PENG收缩特征曲线与收缩各向异性的裂隙率估算模型
2021-06-30张展羽曹德君
王 策,张展羽,,曹德君,陈 于,齐 伟,马 靓
基于VG-PENG收缩特征曲线与收缩各向异性的裂隙率估算模型
王 策1,张展羽1,2※,曹德君3,陈 于4,齐 伟2,马 靓1
(1. 河海大学农业科学与工程学院,南京 211100; 2. 河海大学水利水电学院,南京 210098;3. 南京市长江河道管理处,南京 210011; 4. 江苏省农村水利科技发展中心,南京 210029)
为量化农田裂隙发育程度,考虑脱湿过程中土壤孔隙在基质域、沉降域和裂隙域间转化,该研究提出基于土壤收缩特征和收缩各向异性的裂隙体积比率(裂隙率)关于含水率的预测模型。该模型包括3个子模型:改进VG型式的基质域收缩特征VG-PENG模型,描述收缩各向异性的几何因子Logistic模型,基于上述VG-PENG收缩特征模型和几何因子模型的裂隙率预测模型。通过土壤收缩试验和裂隙演化监测试验,采用图像处理技术提取裂隙数据,评价了该模型的优度及适用性。结果表明,VG-PENG收缩模型具有较好的连续性和明确的物理意义,可精确描述土壤收缩特征(2>0.98);该研究引入Logistic曲线描述土壤收缩几何因子,揭示了收缩过程中土壤横向开裂和纵向沉降的各向异性机理,提出了脱湿初期纵向沉降(几何因子趋近1)、中期主沉降-副开裂(几何因子处于1~3之间)、后期趋于稳定3个阶段,Logistic模型可精确描述收缩几何因子随含水率变化;基于VG-PENG收缩模型和Logistic几何因子模型,构建了裂隙率关于含水率的演化模型,该模型呈“S”型曲线,取决于土壤收缩属性及其各向异性特征,裂隙率模拟值和实测值吻合较好,呈显著水平(2>0.90,<0.001)。该研究裂隙率预测模型修正了土壤收缩各向异性在裂隙率估算中造成的误差,并突破性地将VG-PENG收缩特征曲线进一步推演并应用于裂隙率模拟,可方便、快捷地通过土壤收缩数据预测农田裂隙率随含水率演化规律,为膨缩土裂隙流研究提供理论依据和参数基础。
农田;土壤;干缩裂隙;收缩特征曲线;收缩几何因子;Logistic模型;裂隙率模型
0 引 言
农田干缩裂隙破坏土壤黏聚结构[1],阻隔根系延展[2],其网状大孔隙为水分、溶质迁移提供优先通道,减少水分或营养物质在土壤表层持留时间[3-5],增加农业污染物迁移的危害。裂隙发育具有较强随机性,导致变固相骨架土壤持水、导水特征难以精确模拟[6]。干缩开裂土壤中水分、溶质迁移依赖于裂隙动态变化和土壤水力特征演化,因此,裂隙率量化及预测是裂隙流理论的前提,可为裂隙优先流模型构建提供参数基础[7]。
土壤干湿缩胀是裂隙发育的根本原因,土壤内黏土矿物(包括高岭土、蒙脱石、蛭石等)在干湿过程中产生缩胀效应,导致土颗粒、团聚体重新排列和孔隙体积变化,从而引起土壤体积收缩膨胀现象。通常采用孔隙比和含水率关系描述土壤收缩现象,即土壤收缩特征曲线,该曲线包括结构收缩、线性收缩、残余收缩和零收缩4个阶段。收缩特征曲线作为必不可少的水力参数,用于预测的模型主要有多项式模型、三直线模型、sigmoid模型[8-9]等。Peng等[10]研究发现,基于土壤结构(例如容重、团聚体结构)等可将收缩特征曲线划分为6种型态,且均可采用VG型式的收缩模型模拟。脱湿过程中,土颗粒或团聚体间吸应力导致土壤收缩效应,当颗粒间吸应力大于土壤抗拉强度时产生裂隙[1]。裂隙形态量化是土壤持水、收缩特征与裂隙流模型研究的基础,裂隙在不同质地、黏土矿物类型、有机质含量等因素下呈现出随机网络特征。目前,尚未存在公认的裂隙指标体系,通常采用裂隙率、长度密度、连通性等指标对不同吸力值和含水率状态下的裂隙动态演化进行研究[6,11-15]。
目前常用土壤物理方法(收缩特征曲线)、断裂力学理论方法和裂隙网络随机法3种途径进行裂隙模拟,例如,Vogel 等[16]将土壤间黏聚力简化为弹性弹簧系统断裂问题,提出了基于胡克弹簧系统的裂隙延展模型;Chertkov[17]在细观尺度下对黏性颗粒和团聚体的收缩特征进行模拟,可预测细观尺度有限尺寸条件下的裂隙率随含水率变化;在数值模拟和计算机技术大背景下,研究者也尝试采用LEFM、离散元和有限元方法,对裂隙发育演化问题进行模拟研究[18-22]。基于土壤收缩特征曲线,Stewart等[23]提出了团聚体、沉降域和裂隙域的孔隙随含水率变化物理控制方程,然而未引入土壤收缩各向异性特征。Neely等[24]采用线胀率(Coefficient of Linear Extensibility,COLE)对Bronswijk裂隙体积预测模型进行了改进,合理地预测了田间原位裂隙体积,然而同样忽略了收缩各向异性问题。在土壤裂隙开闭及其优先流研究中,通常过于关注裂隙本身而忽略变形各向异性问题,例如Coppola等[25]构建的裂隙流双渗透模型中,仅考虑裂隙优先通道随含水率的动态愈合过程而忽略了土壤纵向膨缩。土壤膨缩各向异性或裂隙发育程度不均匀性关系到裂隙率预测及其优先流模拟精度,是值得关注的问题。
本文聚焦土壤收缩特征及其各向异性问题,通过揭示孔隙在土壤基质域、沉降域和裂隙域中的形式转变,探索土壤收缩特性与变形各向异性特征关于含水率的动态变化,据此提出考虑收缩特征及其各向异性的裂隙率预测模型,并采用试验和已有文献数据进行验证。
1 裂隙率预测模型理论
土壤收缩或开裂问题的本质是土壤孔隙结构在形态与位置上的转变。本文将脱湿过程土壤孔隙转化作为切入点,首先将VG-PENG收缩特征曲线[10]引入该裂隙率预测模型,其次提出了基于Logistic函数的收缩各向异性模型,最终基于VG-PENG模型和Logistic各向异性模型,构建了裂隙率预测模型,采用试验数据进行验证。
1.1 模型假设和物理描述
1.1.1 裂隙率预测模型假设
1)收缩特征曲线是土壤基本属性,模型仅考虑土壤固、液、气三相物理转化效应;2)根据Stewart等[26]对三维裂隙形态研究,裂隙截面形态为垂直土壤表面的三角形或楔形,因此土壤收缩分量(即横向开裂和纵向沉降)可明确区分;3)土壤开裂过程无外荷载扰动,不存在颗粒运移现象,因此土壤固相质量维持恒定,固、液、气转化服从质量守恒;4)土壤变形或开裂缓慢,因而既定含水率下处于热力学平衡状态,即收缩变形(或裂隙率)与含水率单调对应,可忽略收缩时间效应。
1.1.2 收缩(或开裂)物理描述
模型研究对象为裂隙发育活动区域,其总体积total由固相颗粒(Solid,s)、水分(Water,w)和气体(Air,a)组成。研究区域土壤内体积和质量表示为
式中total、s、w、a和v分别为研究区土壤总体积、土颗粒体积、水分体积、气体体积和孔隙总体积,cm3,下标v表示孔隙(Void),total、s和w分别表示研究区土壤总质量、土颗粒质量和水分质量,g。黏壤土颗粒集聚形成团聚体,团聚体集聚形成土壤基质,土壤孔隙结构呈现出双孔隙特征[23,27-28]。干燥过程中土壤收缩本质为孔隙体积v转化为沉降sub和裂隙体积crack的过程,式(1)可改写为
式中v,agg、sub和crack分别表示基质域中孔隙体积、沉降域体积和裂隙体积,cm3,下标agg表示基质域。
图1a显示了脱湿过程中土壤孔隙从基质域孔隙转化为裂隙和沉降的过程,实线外轮廓体积即为基质域体积,由土颗粒体积、基质内水分和空气体积组成。
注:表示体积,cm3,其下标total、crack、sub、v,agg、a、s和w分别表示体积总量、裂隙体积、沉降域体积、基质域孔隙体积、气相体积、土颗粒体积和水分体积。
Note:is volume, cm3, and the subscript ‘total, crack, sub, v,agg, a, s and w’ denote ‘total volume, crack volume, subsidence volume, porosity volume of aggregated matrix, air phase volume, soil particles volume and water volume’, respectively.
图1 土壤收缩过程中基质域、裂隙域和沉降域随含水率变化
Fig.1 Variations in matrix, crack and subsidence domain with varying water content during soil shrinkage
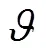
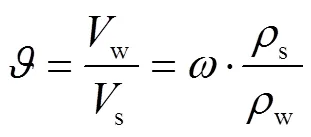
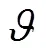
根据脱湿收缩最大路径对土壤含水率和各孔隙率变量去量纲化可得:
且有

1.2 裂隙率预测模型
1.2.1 基质域孔隙率模型——土壤收缩VG-PENG曲线
Peng等[29]研究发现,土壤持水特征曲线与收缩特征曲线具有相似性,均呈现出反曲“S”型特征,据此提出了基于VG模型的收缩特征曲线(VG-PENG模型):

或

1.2.2 沉降域孔隙率模型
引入收缩几何因子s量化土壤横向收缩和纵向沉降的各向异性[30]。在开裂试样中,横向收缩包括裂隙和边界孔隙。在室内尺度,边界效应较小,可将其识别成一种特殊裂隙;在田间尺度,由于农田土壤尺寸较大,边界效应可忽略不计,横向收缩基本等同于干缩裂隙。收缩几何因子s定义为[30]:
或
式中Δ为体积收缩量,cm3,0即为total。0和Δ分别为土层初始厚度和沉降高度,cm。V和H为第次测定时土壤试样体积(cm3)和土层厚度(cm),见图2。
注:、Δ、0和Δ分别为收缩前土壤总体积(cm3)、体积收缩量(cm3)、土样初始厚度(cm)和试样沉降厚度(cm)。
Note:, Δ,0and Δare total soil volume before shrinkage (cm3), change in soil volume (cm3), initial height of soil layer (cm) and vertical subsidence of soil layer (cm), respectively.
图2 干燥过程中土壤纵向沉降和横向收缩(或开裂)示意图
Fig.2 Sketch of soil vertical subsidence and horizontal shrinkage (cracking) during soil drying
对式(11)变形可得:
将式(12)代入式(11)可得:
联立式(10)和式(13)可得:
(14)
式(14)即为沉降域孔隙率预测模型。
1.2.3 裂隙率预测模型
联立式(6)、式(9)和式(15):
可得:
1.3 收缩几何因子模型
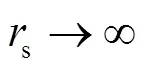
因此,s可根据特征值划分为以下5个区间:
1)s=1.0,土壤基质仅存在沉降变形,无横向收缩;
2)1.0 3)s=3.0,土壤收缩呈现出各向同性特征; 4)s>3.0,土壤基质以水平收缩或开裂为主导,存在微弱纵向沉降; s()~曲线通常呈现出存在上、下阈值的“S”型曲线形状,具有初始值、增长区间、极值和最大斜率等特征参数,因此本文选取资源环境有限条件下的增长规律函数——Logistic模型[31]模拟s()曲线,公式如下: 式中s,max和s,min分别为s()的极大值和极小值,为相对含水率,和分别为平移系数和曲线增长速率系数,对应于斜率极值处的相对含水率。 1)收缩几何因子Logistic模型的可行性及拟合优度; 2)收缩特征曲线VG-EPNG模型的适用性; 3)基于上述2个模型,验证裂隙率模型的预测能力。 拟采用室内收缩试验和开裂试验,以及已公开发表文献资料[32-37]中的实测数据,对上述模型进行验证。 土壤试样取自河海大学江宁节水园区试验场稻麦轮作大田(31°86′N,118°60′E),该地区位于长江中下游,年均降雨量1 106 mm,年均蒸发量900 mm,土壤试样为黏棕壤,隶属于棕色石灰土亚类灰泥土属,总孔隙度为53.5%,年平均日照总时间为2 017.2 h,≥10 ℃积温为4 838.2 ℃。在表层0~40 cm取样过筛后自然风干,将其按田间原表层容重1.30 g/cm3回填至尺寸为22.0 cm(长)× 22.0 cm(宽)×10 cm(高)的有机玻璃容器内,回填土壤质量为699.6 g,试样回填高度精准控制在10 mm,试样厚度采用容器四侧内壁刻度测定,试样初始含水率为4.8%。预湿润过程采用模拟喷灌将400 g蒸馏水均匀喷洒至土壤表面,达到饱和且有1 mm左右微薄层水,放置于室内自然干燥(温度(25±2)℃,相对湿度45%±10%)。脱湿过程中,每8 h拍摄记录裂隙形态以及土壤层厚度(分别测定四边土层厚度求平均),保证相机固定(Canon 60D,18~135 mm镜头)和光源均衡,设置2组重复。同时,采用相同试样在同等环境中测定土壤收缩特征,按原容重将风干土回填至200 cm3的环刀中(直径70 mm,高度52 mm),将试样自下而上饱和处理。脱湿过程中称质量测定试样质量变化,采用游标卡尺(精度0.02 mm)测定试样的直径和高度(各方向测5次求平均值),脱湿结束后置于105 ℃烘箱内烘干,并测定土颗粒质量和干容重,后期推算孔隙率和体积含水比,并绘制其关系曲线。 采用图像批量处理与形态学算法,基于MATLAB R2018a自编Script脚本提取裂隙面积率。截取裂隙图像中心20 cm×20 cm作为研究区域(像素尺寸为2 400×2 400),消除容器边界效应。图像中裂隙区域颜色深度高于基质域,可根据图像灰度直方图分布,采用自适应阈值分割方法优选临界灰度值(),将大于该值的基质域和小于该值的裂隙域区分,分别赋值1和0,输出裂隙二值图像(见图3),统计裂隙像素数量比例,计算裂隙域面积率(cr)[12,38]。试样为薄层土壤,裂隙在发育过程中存在贯穿现象,可近似地将假设中“裂隙剖面呈现出倒三角形或楔形”进一步简化为裂隙矩形剖面,根据土壤层厚度和表面裂隙面积率估算裂隙率,即: 式中cr,i和H分别为第次测定下的裂隙面积(cm2)和 在收缩特征曲线测定中,土壤孔隙比和体积含水比分别采用以下公式进行计算: 式中s和w分别为土颗粒密度和纯水密度,g/cm3,b为土壤干容重,g/cm3,为土壤含水率,g/g。上述参数均可通过环刀内土颗粒质量s,水分质量w和测得的土壤体积V进行推算。 表1 土壤试样物理参数 注:为直径;为高度;RH为相对湿度,NA表示暂无数据。粒径<0.002、0.002~<0.02、0.02~2.0 mm分别为黏粒、粉粒和砂粒。土壤质地以ISSS标准划分。SD,取样深度; SVR,饱和孔隙比;PD,颗粒密度;RVD,残余孔隙比。 Note:is diameter;is height; RH is relative humidity; NA means not available. Particle size <0.002, 0.002-0.02 and 0.02-2.0 mm are clay, silt and sand. Soil texture is classified by ISSS standard. SD, sampling depth; SVR, saturated void ratio; PD, particle density; RVD, residual void ratio. 拟采用决定系数(Coefficient of determination,2)、均方根误差(Root Mean Square Error,RMSE)和平均绝对误差(Mean Absolute Error,MAE),评估模型预测优度,检验模拟值与实测值之间的差异[39]。 表2 收缩几何因子模型拟合参数及拟合优度 注:s,max和s,min分别表示基于Logistic模型拟合的收缩几何因子s的最大值和最小值,和分别为拟合的平移系数和曲线增长速率系数。 Note:s,maxands,minare maximum and minimum shrinkage geometry factor fitted from Logistic model, respectively;andare the fitted translation coefficient and growing velocity factor, respectively. 分析了18组试验数据Logistic收缩几何因子模型的拟合优度,2、RMSE和MAE(见表2)。结果表明,Logistic模型可有效模拟收缩几何因子s()随含水率动态变化,检验结果为极显著水平(<0.001),均方根误差RMSE较小,除第3和4组外,决定系数均大于0.95,均表明Logistic模型具有较高预测精度。其中第3组和4组数据为离散破坏性试验数据,拟合数据的连续性不高,拟合优度相对较低,而其他组均为同组数据在相同干燥路径的连续监测结果,因此数据连续性、光滑性较高。值得注意的是,s极大值、斜率增长速率等参数不同,s()~曲线形态在各土壤间呈现出差异性,该现象反映了s()在不同土壤属性或试样尺寸下的预测难度。 本文基于第1~2组CW1和CW2收缩和开裂试验,以及已发表文献中第5组和第18组实测数据,对式(9)VG-PENG收缩模型进行了验证,评估了模拟值和实测值之间拟合优度,结果详见表3及图5。结果表明,VG-PENG收缩特征模型较好地描述基质域孔隙率随含水率变化过程,各组2>0.98, RMSE<0.04,拟合效果显著,其结果与文献[10]相一致。此外,基于和两参数的Stewart收缩模型同样具有高预测精度,与VG-PENG模型均为连续可导的“S”型函数,为后续裂隙率预测提供了可靠的曲线模型基础。相比之下,VG-PENG收缩模型源起于VG持水曲线模型,具有一定的应用基础。 表3 收缩特征曲线VG-PENG模型和Stewart模型拟合参数及其优度 注:max和min分别表示基质域孔隙率的最大值和最小值,、和分别是基于VG-PENG收缩模型的拟合参数,和分别为Stewart模型的拟合参数; Note:maxandminare the maximum and minimum porosity of matrix domain, respectively;,andare the fitted parameters in VG-PENG model, respectively;andare the fitted parameters in Stewart model. 土壤干燥收缩属性是裂隙发育的根本原因。在细观上,脱湿过程中土壤孔隙水分排出,颗粒或团聚体间形成弯液面,内部产生的基质吸力或毛管力驱使颗粒间产生相互吸引的吸应力,土壤骨架结构(包括颗粒和团聚体结构)趋于紧密排列,孔隙体积减小,进而产生宏观收缩效应。土壤收缩特征曲线可分为4个阶段:1)结构收缩,2)线性收缩,3)残余收缩和4)零收缩[10,33]。结构收缩发生于存在团聚体大孔隙结构的原状土内,此时大孔隙迅速排水,团聚体骨架未见明显变化;在线性收缩阶段,孔隙比和体积含水比斜率值趋近于1,排出水分体积完全转化为孔隙变形,此时团聚体内孔隙趋于近饱和状态;当气体进入团聚体内部时(进气点),孔隙体积变化量开始小于水分排出量,土壤团聚体开始收缩变形。 然而,该模型假设土壤含水率纵向分布均匀,未考虑大田尺度层间含水率异质性,因此需推广其在田间原状土中的应用。此外,该模型仅考虑脱湿收缩过程,土壤变形时间效应可忽略,然而在干湿交替过程中,土壤水力特征存在脱湿-吸湿滞后现象,能否采用膨胀特征曲线模拟裂隙闭合演化过程,并将该模型在干湿循环中进一步推广,可在后期进行探究。 1)根据孔隙在基质域、沉降域和裂隙域之间转化过程,构建了裂隙率关于含水率的动态演化模型。该模型包括3个子模型:基于VG-PENG收缩特征曲线的基质域孔隙率模型;描述变形各向异性的收缩几何因子Logistic模型;综合VG-PENG模型和Logistic模型的裂隙率预测模型。 2)VG型式的VG-PENG收缩特征曲线模型包括2个估算参数和3个拟合参数,可精确模拟多种类型土壤收缩特征,拟合效果显著(2>0.98, RMSE<0.04)。 3)引入Logistic模型描述土壤收缩几何因子,多种土壤数据表明,土壤收缩呈现出各向异性:脱湿初期仅纵向沉降,脱湿中期主要表现为纵向沉降,同时伴随着水平收缩或开裂,脱湿后期趋于稳定。Logistic模型可精确模拟收缩几何因子随含水率变化过程,实测值和模拟值呈显著相关性(2=0.964,<0.001)。 4)基于VG-PENG收缩模型和几何因子Logistic模型,构建了裂隙率预测模型。实测值和模型模拟值之间呈极显著水平,该模型补足了收缩各向异性导致的裂隙率预测误差,可为后续裂隙优先流模拟提供参数基础。 [1] Yesiller N, Miller C J, Inci G, et al. Desiccation and cracking behavior of three compacted landfill liner soils[J]. Engineering Geology, 2000, 57(1/2): 105-121. [2] Mawodza T, Burca G, Casson S, et al. Wheat root system architecture and soil moisture distribution in an aggregated soil using neutron computed tomography [J]. Geoderma, 2020, 359(2): 113988. [3] Allaire S E, Roulier S, Cessna A J. Quantifying preferential flow in soils: A review of different techniques[J]. Journal of Hydrology, 2009, 378(1/2): 179-204. [4] Zhang Z B, Peng X, Zhou H, et al. Characterizing preferential flow in cracked paddy soils using computed tomography and breakthrough curve[J]. Soil & Tillage Research, 2015, 146(2): 53-65. [5] Beven K, Germann P. Macropores and water flow in soils revisited[J]. Water Resources Research, 2013, 49(6): 3071-3092. [6] Wang C, Zhang Z Y, Liu Y, et al. Geometric and fractal analysis of dynamic cracking patterns subjected to wetting-drying cycles[J]. Soil & Tillage Research, 2017, 170(6): 1-13. [7] Vogel H J, Hoffmann H, Roth K. Studies of crack dynamics in clay soil-I. Experimental methods, results, and morphological quantification[J]. Geoderma, 2005, 125(3/4): 203-211. [8] Groenevelt P H, Grant C D. Curvature of shrinkage lines in relation to the consistency and structure of a Norwegian clay soil[J]. Geoderma, 2002, 106(3/4): 235-245. [9] 吕殿青,邵明安. 土壤干湿收缩特征研究进展[J]. 土壤通报,2003,34(3):225-228. Lv Dianqing, Shao Ming’an. A review of soil shrinkage characteristics[J]. Journal of Soil Science, 2003, 34(3): 225-228. (in Chinese with English abstract) [10] Peng X, Horn R. Identifying six types of soil shrinkage curves from a large set of experimental data[J]. Soil Science Society of America Journal, 2013, 77(2): 372-381. [11] DeCarlo K F, Shokri N. Effects of substrate on cracking patterns and dynamics in desiccating clay layers[J]. Water Resources Research, 2014, 50(4): 3039-3051. [12] Wang C, Zhang Z Y, Qi W, et al. Morphological approach to quantifying soil cracks: Application to dynamic crack patterns during wetting-drying cycles[J]. Soil Science Society of America Journal, 2018, 82(4): 757-771. [13] Tang C S, Shi B, Liu C, et al. Experimental characterization of shrinkage and desiccation cracking in thin clay layer[J]. Applied Clay Science, 2011, 52(1/2): 69-77. [14] 张中彬,彭新华. 土壤裂隙及其优先流研究进展[J]. 土壤学报,2015,52(3):477-488. Zhang Zhongbin, Peng Xinhua. A review of researches on soil cracks and their impacts on preferential flow[J]. Acta Pedologica Sinica, 2015, 52(3): 477-488. (in Chinese with English abstract) [15] 李文杰,张展羽,王策,等. 干湿循环过程中壤质黏土干缩裂缝的开闭规律[J]. 农业工程学报,2015,31(8):126-132. Li Wenjie, Zhang Zhanyu, Wang Ce, et al. Propagation and closure law of desiccation cracks of loamy clay during cyclic drying-wetting process[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(8): 126-132. (in Chinese with English abstract) [16] Vogel H J, Hoffmann H, Leopold A, et al. Studies of crack dynamics in clay soil - II. A physically based model for crack formation[J]. Geoderma, 2005, 125(3/4): 213-223. [17] Chertkov V Y. Physical modeling of the soil swelling curve vs. the shrinkage curve[J]. Advances in Water Resources, 2012, 44(10): 66-84. [18] Hirobe S, Oguni K. Coupling analysis of pattern formation in desiccation cracks[J]. Computer Methods in Applied Mechanics and Engineering, 2016, 307(10): 470-488. [19] Thi Dong V, Pouya A, Hemmati S, et al. Numerical modelling of desiccation cracking of clayey soil using a cohesive fracture method[J]. Computers and Geotechnics, 2017, 85(5): 15-27. [20] Sima J, Jiang M, Zhou C. Numerical simulation of desiccation cracking in a thin clay layer using 3D discrete element modeling[J]. Computers and Geotechnics, 2014, 56(3): 168-180. [21] Sanchez M, Manzoli O L, Guimaraes L J N. Modeling 3-D desiccation soil crack networks using a mesh fragmentation technique[J]. Computers and Geotechnics, 2014, 62(8): 27-39. [22] 沈珠江,邓刚. 黏土干湿循环中裂缝演变过程的数值模拟[J]. 岩土力学,2004,25(增刊2):1-6,12. Shen Zhujiang, Deng Gang. Numerical simulation of crack evolution in clay during drying and wetting cycle[J]. Rock and Soil Mechanics, 2004, 25(Z2): 1-6, 12. (in Chinese with English abstract) [23] Stewart R D, Rupp D E, Najm M R A, et al. A unified model for soil shrinkage, subsidence, and cracking[J]. Vadose Zone Journal, 2016, 15(3): 1-15. [24] Neely H L, Morgan C L S, McInnes K J, et al. Modeling soil crack volume at the pedon scale using available soil data[J]. Soil Science Society of America Journal, 2018, 82(4): 734-743. [25] Coppola A, Comegna A, Dragonetti G, et al. Simulated preferential water flow and solute transport in shrinking soils[J]. Vadose Zone Journal, 2015, 14(9): 1-22. [26] Stewart R D, Najm M R A. Field measurements of soil cracks[J]. Soil Science Society of America Journal, 2020, 84(5): 1462-1476. [27] Li X, Zhang L M. Characterization of dual-structure pore-size distribution of soil[J]. Canadian Geotechnical Journal, 2009, 46(2): 129-141. [28] Wang G, Wei X. Modeling swelling-shrinkage behavior of compacted expansive soils during wetting-drying cycles[J]. Canadian Geotechnical Journal, 2015, 52(6): 783-794. [29] Peng X, Horn R. Modeling soil shrinkage curve across a wide range of soil types[J]. Soil Science Society of America Journal, 2005, 69(3): 584-592. [30] Bronswijk J B. Shrinkage geometry of a heavy clay soil at various stresses[J]. Soil Science Society of America Journal, 1990, 54(5): 1500-1502. [31] 王海军,刘艺明,张彬,等. 基于Logistic-GTWR模型的武汉城市圈城镇用地扩展驱动力分析[J]. 农业工程学报,2018,34(19):248-257. Wang Haijun, Liu Yiming, Zhang Bin, et al. Analysis of driving forces of urban land expansion in Wuhan metropolitan area based on Logistic-GTWR model[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(19): 248-257. (in Chinese with English abstract) [32] Sanchez M, Atique A, Kim S, et al. Exploring desiccation cracks in soils using a 2D profile laser device[J]. Acta Geotechnica, 2013, 8(6): 583-596. [33] Peng X, Horn R. Anisotropic shrinkage and swelling of some organic and inorganic soils[J]. European Journal of Soil Science, 2007, 58(1): 98-107. [34] Chertkov V Y, Ravina I, Zadoenko V. An approach for estimating the shrinkage geometry factor at a moisture content[J]. Soil Science Society of America Journal, 2004, 68(6): 1807-1817. [35] Chertkov V Y. The shrinkage geometry factor of a soil layer[J]. Soil Science Society of America Journal, 2005, 69(6): 1671-1683. [36] Huang C, Shao M, Tan W. Soil shrinkage and hydrostructural characteristics of three swelling soils in Shaanxi, China[J]. Journal of Soils and Sediments, 2011, 11(3): 474-481. [37] 刘平,张虎元,严耿升,等. 土建筑遗址表部土体收缩特征曲线测定[J]. 岩石力学与工程学报,2010,29(4):842-849. Liu Ping, Zhang Huyuan, Yan Gengsheng, et al. Determination of soil shrinkage characteristic curve of surface soil on ancient earthen architectures[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(4): 842-849. (in Chinese with English abstract). [38] 张展羽,朱文渊,朱磊,等. 根系及盐分含量对农田土壤干缩裂缝发育规律的影响[J]. 农业工程学报,2014,30(20):83-89. Zhang Zhanyu, Zhu Wenyuan, Zhu Lei, et al. Effects of roots and salinity on law of development for farmland soil desiccation crack[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(20): 83-89. (in Chinese with English abstract) [39] 朱磊,马荣,范东峻,等. 考虑相关长度的土壤开裂模型改进及其参数对裂隙形态的影响[J]. 农业工程学报,2018,34(24):123-131. Zhu Lei, Ma Rong, Fan Dongjun, et al. Soil cracking improved model considering with correlation length and effect of its parameters on crack morphology[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(24): 123-131. (in Chinese with English abstract) Crack porosity estimation model based on VG-PENG shrinkage characteristic curve and soil shrinkage anisotropy Wang Ce1, Zhang Zhanyu1,2※, Cao Dejun3, Chen Yu4, Qi Wei2, Ma Liang1 (1.,,211100,; 2.,,210098,; 3.210011,; 4.,210029,) Soil shrinkage and cracking are essential behavior during dehydration in the environmental geotechnical engineering of farmland. Their quantification can be necessary to determine the soil physical-hydraulic parameters and crack preferential flow in soils. In the present study, a new predicting model was proposed for the crack ratio with respect to soil water content using a VG-based soil shrinkage characteristic curve and soil shrinkage anisotropy factor. The migration and transition of pores were also considered in the solid-liquid-gas phase system in soil matrix-subsidence-crack domains. This model included a VG-based soil shrinkage characteristic model, a shrinkage anisotropy model using a Logistic curve, and the soil cracking ratio model. An indoor experiment was conducted to investigate the soil shrinkage characteristics and cracking behavior. The crack ratio was determined using image processing techniques and morphological features. The experimental data was used to evaluate the fitting of a model for cracking ratio evolution. The results showed that the VG-based shrinkage model (VG-PENG model),three fitting parameters, and two estimated parameters, well predicted the soil shrinkage characteristics in various types of soils (2>0.97, RMSE<0.04). The Logistic model was first introduced into the expression of soil shrinkage geometry, which was previously used to describe the growth principles under limited resources. Quantification of soil shrinkage anisotropy showed that the soil shrinkage was highly anisotropic. The soil shrinkage exhibited only subsidence with shrinkage geometric factor approximately equivalent to 1 in the early phase of the soil dehydration. The shrinkage showed mainly vertical subsidence with a light horizontal shrinkage (or cracking) in the middle phase, with shrinkage geometric factor varying between 1 and 3. The shrinkage geometry factor tended to be stabilized in the late phase, indicating a residual state of shrinkage. The anisotropic shrinkage with rapid change occurred in the relative water content of 0.3-0.7. The logistic shrinkage anisotropy model well predicted the shrinkage geometric factor with respect to the water content. A new model was also proposed to predict the evolution of crack ratio with respect to water content. The curve of the model showed sigmoid characteristics, depending highly on shrinkage properties and anisotropy. The simulated data showed better agreement with the experimental one, indicating an extremely significant level (2=0.974,<0.001). Since the water content within the soil layer was assumed evenly distributed, this model was considered to be appropriate in a relatively limited height of the soil layer. The evolution of crack ratio was predicted from a perspective view of soil physics rather than a mechanical view. Consequently, the soil shrinkage anisotropy was fully integrated into the modelling of the cracking ratio. A significant innovation was also made to apply the VG-type shrinkage characteristic curve to crack ratio prediction. The crack porosity prediction belonged to the field of soil physics to describe the evolution of cracking ratio using the shrinkage curve and geometry factor. The proposed model well predicted the cracking ratio in surface soils with high accuracy and convenience. A further investigation was also needed to explore the efficacy of the crack ratio model on undisturbed soils, and the effects of substrate properties on cracking behaviors. The research can provide a promising theoretical basis and parameter prediction for soil water-solute movement in soils with variable-solid phase and preferential flow in soil physics and hydrology. farmlands; soils; cracks; shrinkage characteristic curve; shrinkage geometry factor; Logistic model; crack porosity model 2020-12-10 2021-01-31 国家自然科学基金面上项目(51879071);江苏省自然科学基金青年基金项目(BK20200523);中央高校基本科研业务费专项资金资助(B200201017);江西省重点研发一般项目(20203BBGL73226) 王策,博士,讲师,研究方向为农田裂隙及其优先流理论、高效灌排理论。Email:wangce@hhu.edu.cn 张展羽,博士,教授,研究方向为节水灌排及农业水资源高效利用。Email:zhanyu@hhu.edu.cn 10.11975/j.issn.1002-6819.2021.07.014 S278 A 1002-6819(2021)-07-0112-10 王策,张展羽,曹德君,等. 基于VG-PENG收缩特征曲线与收缩各向异性的裂隙率估算模型[J]. 农业工程学报,2021,37(7):112-121. doi:10.11975/j.issn.1002-6819.2021.07.014 http://www.tcsae.org Wang Ce, Zhang Zhanyu, Cao Dejun, et al. Crack porosity estimation model based on VG-PENG shrinkage characteristic curve and soil shrinkage anisotropy[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(7): 112-121. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2021.07.014 http://www.tcsae.org1.4 模型验证与评估


2 材料与方法
2.1 供试土样及其裂隙演化试验
2.2 图像处理与参数提取


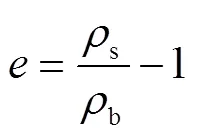

2.3 文献数据提取


2.4 统计分析及模型评价指标
3 结果与分析
3.1 收缩几何因子模型
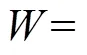

3.2 收缩特征曲线VG-PENG模型

3.3 裂隙域孔隙率预测模型验证
4 讨 论
4.1 土壤收缩各向异性及裂隙发育机理

4.2 裂隙率预测模型优度分析
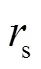

5 结 论
