考虑供应中断和货损的供应商选择与订货分配决策

王婧，叶勇，罗红恩

（1.安徽农业大学，合肥230036；2.农业农村部农产品电子商务重点实验室）

近年来，生鲜农产品电子商务发展迅速。采购决策是电商企业获得经济效益和竞争优势的关键。生鲜农产品是指农业生产部门未经加工或者很少加工而生产的初级农产品。它们在室温下容易变质，影响产品质量、价格和顾客满意度。生鲜农产品电商卖家首先需要选择合适的供应商，然后确定合适的采购品种和数量。

在供应商选择方面，一般分为单供应商决策和多供应商决策。单个供应商往往管理良好，可以建立长期稳定的合作关系，但如果出现供应失败，则会导致整个供应链的失败。多个供应商可以更好的规避风险，这有利于供应链的稳定，但往往管理变得更加困难。生鲜农产品电子商务供应链的产品范围普遍较广，单一的供应商很难提供全部产品，通常需要多个供应商来提供产品。主要讨论了电子商务卖家如何从候选供应商中选择多个供应商来满足多种生鲜农产品的销售需求。

近年来，供应链风险显著增加，供应商中断被认为是供应链风险的主要表现之一。在Deloitte进行的一项调查中，71%的受访者认为供应链风险是公司战略决策的关键因素。供应商中断导致增加采购和物流成本，卖方往往被迫寻求并选择新的供应商迅速从其他地方采购，并加快运输，以保持服务水平。关注在供应中断风险和货物损失条件下，农产品电子商务卖家的采购决策。

1 文献综述

1.1 供应商选择

农产品电商卖家组织销售运营，首先需要选择恰当数量的供应商。与少量的甚至单一的供应商建立长期的、稳定的合作关系，能够使企业获得质量和成本的保证。另一方面，供应商数量的缩减尤其是减为单一供应商，将会增加供应链对抗风险的脆弱性[1]。多供应商选择问题已有大量的研究成果。牟能冶、常建鹏和陈振颂[2]从社会绩效、环境绩效与经济绩效三方面构建了可持续供应商评估指标体系。陈可嘉等[3]研究了供应链中断风险下最优供应商数量决策模型，模型以采购总成本最小为目标。周清华等[4]利用直觉模糊集理论和TOPSIS决策方法研究了绿色供应商选择问题。方健等[5]研究了随机需求下考虑碳排放的供应商选择问题。以上文献考虑了不同的因素环境下的供应商选择问题，但是研究中都没有联合考虑需求分配的问题。

1.2 供应商选择与订单分配联合决策

现有供应商选择和订单分配的研究已经取得了重要成果和进展。根据是否考虑供应中断风险，可以把这些文献分为两类。第一类是没有考虑中断风险的供应商选择和订单分配研究。第二类是考虑了供应中断风险的供应商选择和订单分配文献。

第一类没有考虑中断风险。蒋琦玮、秦进等[6]研究了需求数量和需求时机不确定环境下的供应商选择和订货量分配优化模型，该模型考虑采购成本、运输成本、退货成本以及交付晚点率、并以废品率最小和供应商柔性最大为优化目标。并基于模拟退火算法设计了启发式求解方法。王林等[7]研究了随机需求环境下的供应商优选和订货量分配问题。以质量、成本和交货期为目标，借助加权法和罚函数法将多目标转化为单目标。这些文献多考虑问题的随机不确定性，但没有考虑中断风险。

黄辉等[8]研究了多产品、多价格折扣、供应商产能约束和需求量为模糊值等约束条件下的多供应商联合供货时的订单分配问题。Pankaj Gupta等[9]针对多目标多物资供应商选择和订单分配价格折扣问题，建立了模糊多目标整数线性规划与层次分析法相结合的优化模型，并提出了一种加权概率规划方法求解优化模。Kannan等[10-11]重点研究造纸行业中最佳绿色供应商的选择和潜在供应商的订单分配。该模型包含两阶段混合方法。第一阶段通过考虑经济因素（成本）、运营因素（质量和交付）、环境标准（回收能力和温室气体排放控制），采用模糊排序技术，对潜在供应商进行评级和选择。第二阶段采用多目标线性规划方法进行订单分配，使生产过程中的成本、物料报废、延迟交货、废物回收和二氧化碳排放最小化。这些文献多考虑了问题的模糊不确定性，但都没有考虑供应中断风险和货损。

第二类考虑了中断风险。李占丞、刘晓冰等[13]研究了多个供应商和单个制造商组成的二级供应链背景下，面向生产过程的供应商选择与订货量分配模型。模型考虑了允许供应商延期交货且脱期时间依赖供应商可靠度的情形。总成本考虑了脱期惩罚成本。李占丞、刘晓冰等[12]研究双源采购环境下，供应商交货数量不确定情况下，装配型制造企业将订货量分配和订单排产进行联合决策的问题。与上面两篇文章不同的是，研究的电商卖家的供应商选择和订货量分配分配问题，不涉及生产过程。潘伟[13]将随机需求、供应中断风险及价格折扣等联合起来研究订单分配问题，构建了模糊多目标模型。但其只研究单一物资品种的情况。卢志刚等[14]考虑了供应量可靠性，研究了多产品的供应商订货量分配问题，利用罚函数法将多约束优化转化为无约束，设计了蛙跳粒子群算法进行求解。

Purushottam Lal Meena等[15]考虑了供应商的中断概率、容量限制和基于数量的价格折扣，构建了供应商选择和需求分配模型，并提出了新的求解算法。F.Vahidi等[16]研究了运作和中断风险下可持续供应商选择和订货分配问题，构建了一个双目标两阶段混合随机规划模型。目标是选择一个弹性可持续的供应基地。考虑了备份供应商的契约，以及供应节点的过剩产能。F.Hamdi等[17]研究了订货性生产环境，存在中断风险供应商时的供应商选择和订货分配问题。分别从风险中性和风险厌恶型决策者角度构建了两个混合整数规划模型。Elham Esmaeili-Najafabadi等[18]提出了考虑中断风险的集中式供应链供应商选择和订单分配的混合整数非线性规划模型。使用了被选择供应商的保护政策和被保护供应商的紧急库存分配政策。中断概率的高低一定程度上影响了供应链的决策。S.A.Torabi等[19]提出了一种双目标混合概率、两阶段随机规划模型，以解决供应商选择和订单分配的问题，建立运行和中断风险下的弹性供应基础。模型采用了供应商的业务连续性计划、加强供应商和与备用供应商签订合同等前瞻性策略，以提高选定供应基地的弹性水平。以上文献从一定角度考虑了供应中断风险，都没有考虑农产品供应过程中货物的损耗。

关于易腐品供应链的采购供应，相关的文献很有限。张莉、胡小建、卢朝东等[20]研究外部需求为三角模糊数的情况下，易腐品供应链中零售商的订货量决策问题。但该文献只考虑单一供应商情况下的采购决策，且未考虑供应商供货中断风险。研究的是多供应商的优选决策。V.R.Ghezavati1等[21]以西红柿为例，从经销商的角度研究了生鲜农产品收割后供应的周期决策模型，以经销商收益最大化为目标。每个顾客收到的产品质量有差异，因此需要根据顾客满意度水平合理定价。模型对农产品的等级考虑新鲜度和成熟度。农产品收割后的成熟度被量化，同时设计了品质损失函数。

综上所述，在考虑供应中断和产品损耗情况下供应商选择和订单分配问题仍有研究空间。主要从生鲜农产品电商卖家的视角，研究在考虑供应商中断风险和采购过程中货物损失风险下，采购生鲜农产品时供应商选择和订货量分配的决策问题。模型研究的是多产品的决策问题，以供应成本最小化为目标，考虑采购中货物损失对采购量的影响，以及供应量可靠性的要求。

2 问题描述与模型构建

电商企业通过某种定性遴选机制已经确定了N个备选供应商。N个备选供应商能够提供同质化的M种生鲜农产品。备选供应商到电商企业物流中心的运输时间、运输距离和运输成本不同，同时每个备选供应商的中断概率不同。生鲜农产品电商企业采购的农产品在其物流中心进行存储、加工和处理。电商企业需求预测已知的前提下，从N个备选供应商中选择合适的供应商供货，形成稳定可靠的供应网络是研究的主要问题。生鲜农产品电商企业供应网络示意图如图1所示。

2.1 模型假设

（1）所有备选供应商的可供应量之和能够满足电商企业的销售需求；

（2）所有备选供应商的单位采购成本、单位运输成本和固定成本已知；

（3）所有采购的物资在电商企业的物流中心进行汇集，存储加工和处理；

（4）电商企业在物流中心的单位物资储存成本和单位物资加工处理成本已知；

（5）备选供应商到电商企业的物流中心的单位物资运输成本，与两地之间的运输时间存在某种线性关系。

2.2 符号含义

i：表示备选供应商索引。i=1，2，…n。

k：表示采购的产品项。k=1，2，…m。

φik：表示从供应商i运输生鲜农产品k到电商物流中心过程中的损耗比例系数，该系数与供应商i到电商企业物流中心运输时间。

βik：表示从供应商i运输生鲜农产品k到电商物流中心后该生鲜农产品有效比例因子。

Dk：表示电商企业预测的生鲜农产品k的市场总需求量。

Sik：表示供应商i稳定供应生鲜农产品k的概率。

rik：表示供应商i供应生鲜农产品k过程中，发生供货中断的概率。

mik：表示供应商i要求销售生鲜农产品k的最小批量。

cvik：表示从供应商i运输生鲜农产品k到电商企业物流中心的单位运输成本。

cpik：表示电商企业向供应商i采购生鲜农产品k的单位采购成本。

fi：表示电商企业向供应商i购货的固定成本。

csk：表示物流中心对采购来的生鲜农产品k加工处理的单位处理成本。

Hk：表示物流中心对生鲜农产品k的单位库存成本。

Lik：表示供应商i对生鲜农产品k的最大可供货量。

r*k：表示电商企业对生鲜农产品k的期望容忍可靠性。

xik：表示电商企业向供应商i采购生鲜农产品k的订货量。

yi：表示供应商i是否被选择成为供货商。当供应商i被选择供货时，其值为1；否则，其值为0。

Zik：表示供应商i是否被选择供应产品k。当供应商i被选择供应产品k时，其值为1；否则，其值为0。

2.3 模型构建

在研究中，考虑了采购成本运输成本、供应商订货固定成本、以及配送中心的库存和加工成本。在满足供应链可靠性前提下，考虑供应点的不同货损，选取总成本最优的多物资采购方案。构建的规划模型如下：

公式（1）是目标函数，包括三个部分，第一部分表示采购和运输成本，第二部分表示供应商订货固定成本，第三部分是配送中心的库存和加工成本。目标是三部分之和最小。公式（2）表示考虑了有效比例因子的总订货量应能满足总需求。公式（3）表示生鲜农产品有效比例因子与损耗比例系数和为1。公式（4）表示向供应商i的订货量不能超过其最大可供货量。公式（5）表示向供应商i的订货量应满足其最小订货量的要求。公式（6）表示供应商中断概率和可靠性概率之和为1。公式（7）表示供应系统可靠性应大于等于期望容忍可靠性。公式（8）表示供应商的供应量为正整数。公式（9）表示供应商是否被选供货，如果被选上，yi值为1，否则值为0。公式（10）表示供应商i是否被选择供应产品k，如果被选上，zik值为1，否则值为0。公式（11）表示如果供应商i被选择供应至少一种产品，那么yi值为1，如果供应商i没有被选择供应任何产品，那么yi值为0。

3 基于改进差分算法的求解策略

模型是带约束的非线性整数规划，约束（2）（7）和（11）的处理成为求解的关键。yi是中间变量，只要zik确定，根据公式（11）自然可以确定，所以，关键决策变量是xik和zik。关键约束是（2）和（7）。在差分算法的基础上，利用枚举法和类似冒泡排序，以及边界修复策略实现求解近似最优解。算法的基本流程如图2所示。算法的主要技术步骤如下所述。

图2 基于冒泡排序的差分算法流程图Fig.2 Flow chart of improved difference algorithm based on bubble sorting

3.1 编码方案

采用整数和自然数结合的两段编码方法，对xik采用整数编码，对zik采用自然数编码，yi是中间变量，进行隐性01编码。xik的取值范围在zik确定的前提下，根据公式（4）和（5）很容易确定。zik的确定是关键。通过枚举法可给出满足约束条件（7）的所有方案集合。这些方案集合的索引号即为zik的自然数编码值。

第一段是对xik采用整数编码，前面n位分别代表第n个供应商对第1种物资的供应方案，后面依次是n个供应商对第k种物资的供应方案，直到最后一种物资即第m种物资供应方案确定而结束，如图3所示。

图3 对xik的编码示例Fig.3 An example of encoding for xik

第二段是对zik进行自然数编码，第1个位置代表对第1种物资各供应商是否供货的索引，它是一个自然数。第k个位置代表对第k种物资各供应商是否供货的索引，它也是一个自然数。有m种物资，所以这部分总共有m个编码位。在此过程中，需要先判断各供应商构成的供应链，是否满足可靠性要求，即满足约束条件（7）；然后，把所有可行的供货商组合放到一个动态集合中，那么zik就在这些组合中选择，选中的一种组合，即表示对该物资供货的供应商选择方案，对应的索引号即为本编码位的值。如图4所示。

图4 对zik的编码示例Fig.4 An example of encoding for zik

3.2 约束处理

约束（7）的处理是采用枚举法。通过枚举法给定所有满足供应链可靠性要求的方案集合，即确定了满足约束（7）的所有的zik能组合。

约束（2）的处理是借鉴Thomas P.Runarsson和Xin Yao在文献[22]中提出的类似冒泡排序的随机排序策略。它非常好的解决了罚函数法的惩罚系数难确定的问题。大量研究已经表明了其优越性。目标函数可缩写为（fx）。约束（2）经过变形可表示为函数为g（x），见公式（12）。

3.3 修复策略

对于带约束条件的非线性规划，如何使种群个体在可行域内是求解有效性的关键。研究设计了一个边界条件修复策略和约束条件修复策略。

（1）边界条件修复策略

边界条件修复策略是使生成的种群xik始终满足公式（4）和（5）给定的边界约束，如果不在这个边界范围，就在边界范围内随机生成一个新个体。

（2）约束条件修复策略

约束条件修复策略是针对约束条件（2）设计的修复策略。如果个体不满足约束条件（2），对该个体进行修复，形成可行解。通过修复策略很好的将种群个体限定在可行域范围内。

定义约束条件（2）变型的函数h（x）见公式（13），它是判断个体是否超出约束的依据。

遍历种群中每个个体xik，对应的h（x）的值有三种可能的情况。

（1）h（x）＞0时，找到个体xik的最大值的基因位，让该基因位的数据等于当前值减去h（x）/βik，并进行四舍五入。

（2）h（x）＜0时，找到个体xik非零最小值的位置；个体非零最小值处的数据等于当前值减去h（x）/βik，并进行四舍五入。

（3）h（x）=0时，个体xik本身是可行解，直接进入下一个循环。

4 数值实验

4.1 实验数据

部分实验数据来源于卢志刚和戚庆禹[14]的文献。某家电子商务企业从5个供应商中进行选择供货3种生鲜农产品。物流中心对采购来的生鲜农产品加工处理的单位处理成本分别为6，5，5.5。物流中心的单位库存成本分别3，2，2。供应系统期望容忍可靠性为0.9。向各供应商采购的固定成本一次是1 000、800、900、1 000、800。其他参数值见表1所示。

表1 各类农产品向各供应商采购时的相关实验数据表Table 1 Experiment data on the three kinds of agricultural products purchased from five suppliers.

4.2 改进的差分算法实验过程及结果

在matlab2016环境下，应用改进的差分算法进行编程求解，设置交叉概率位0.1和变异概率为0.4，最大迭代代数为200，结果如下图5所示。从图5可以看出，大约在50代左右算法开始收敛于最优解。

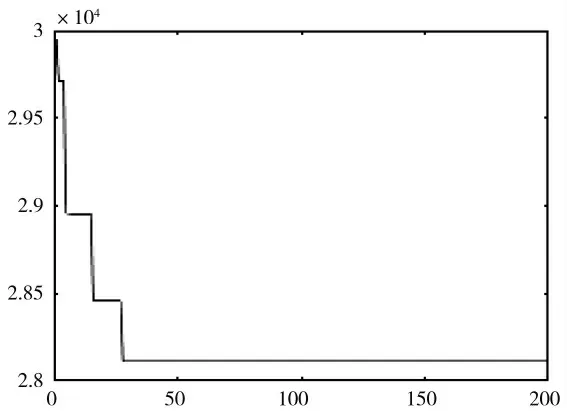
图5 改进的差分算法求解结果图Fig.5 Results of the improved differential evolution algorithm

对交叉概率和变异概率进行参数寻优实验。将最大的迭代代数设置为200，使交叉概率和变异概率分别在0.1到1之间，以0.1步长增加变化。这样，有100种配对组合。在每种配对下，程序运行30次。求解的最优目标函数的平均值和最小值分别见表2和表3。从表2和表3结果可以看出，当交叉概率为0.1，变异概率的初始值是0.3和0.4，模型的目标函数值的平均值是28 068，而目标函数的全局最小值也是28 068，算法性能最好。同时，在许多概率组合中，改进的差分进化算法也得到了相同的目标函数最小值，即28 068。相应的最优物资供应方案如表4所示。

表2 交叉概率和变异概率组合变化结果下的目标函数值平均值Table 2 The average value of the objective function under the combination of crossover probability and mutation probability

表3 交叉概率和变异概率组合变化结果下的目标函数值最小值Table 3 The minimum value of the objective function under the combination of crossover probability and mutation probability

表4 最优分配方案Table 4 Optimal allocation scheme

4.3 对比实验

为了验证算法的有效性，作者随机生成6组不同规模的实验数据，包括物资种类数、供应商数量、货损率、供应链期望容忍可靠性等。针对实验数据，以LINGO的分支定界法和改进的遗传算法开展了对比实验。每种实验规模的数据，程序运行30次，记录并计算目标函数值的平均值、最小值和运行时间。改进的遗传算法是以标准遗传算法为基础，应用前文设计的修复策略和类似冒泡排序策略形成。每种实验规模的数据，程序运行30次，记录求解的最优目标函数的平均值、最小值和运行时间。具体实验结果如表5所示。分析结果发现：

表5 三种算法的测试结果Table 5 Test results for the three algorithms

（1）在目标函数值的最小值方面，改进的差分进化算法和改进的遗传算法的性能明显优于LINGO求解。改进的差分进化算法略优于改进的遗传算法。

（2）在目标函数值平均值方面，改进的差分进化算法的性能始终优于其他两种算法。

（3）平均运算时间方面，改进的差分进化算法始终优于改进的遗传算法，随着实验规模的增加，改进的差分进化算法优于LINGO的表现。

总体而言，改进的差分进化算法的性能随着数据量的增加优势越来越明显。改进的差分进化算法是有效和可行的。

5 敏感性分析

因为最优决策方案可能受到模型参数取值的影响，所以主要考察了这些参数对目标函数值的影响。这些参数包括Mik、Lik、Hk、fi、rik、CVik、CPik、r*k、csk、βik和Dk。以初始参数值为基准，在-15%和15%范围内按5%的比例依次改变各参数值。当一个参数的值改变时，其他参数的参考值保持不变。随机选取前文第一组试验数据作为基础数据，求解的目标函数值如表6所示。

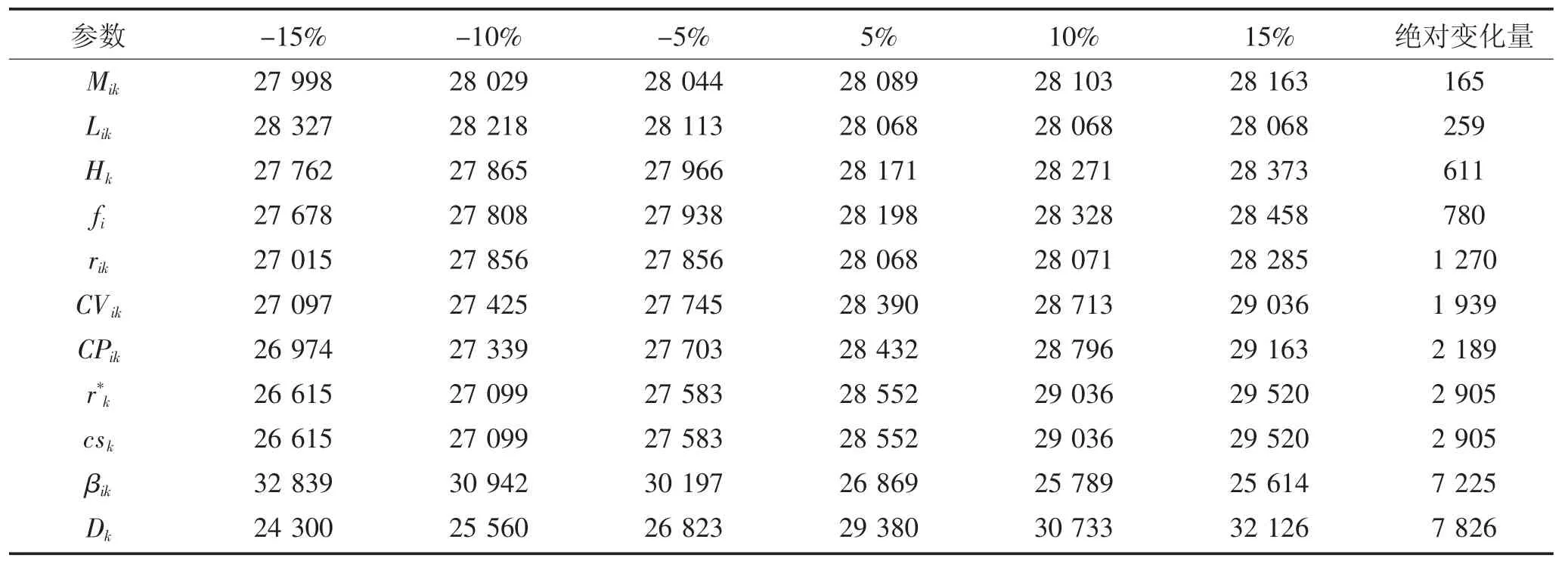
表6 参数的敏感性分析Table 6 Sensitivity analysis of parameters

在表6中，第8列描述了参数增加和减少15%时目标函数值变化的绝对值。根据各参数对目标函数值的影响程度，将各参数分为四个灵敏度等级。一级的参数包括Dk和βik；即总成本是随Dk和βik的变化最敏感，总成本跟这两个参数值是最强的正相关。因此，在优化模型时，应尽可能准确地设置参数值。二级参数包括r*k、CVik、CPik、r*k和csk。这五个参数与总成本有很强的正相关关系，也就是说，模型对它们的变化很敏感。三级的参数为rik、fi和Hk。这三个参数与总成本呈弱正相关，也就是说，模型通常对它们的变化敏感性较弱。四级的参数包括Lik和Mik。这两个参数与总成本的正相关关系非常弱，也就是说，模型对其变化不那么敏感。

6 结论

研究供应中断和存在货损情况下，生鲜农产品电子商务卖家的供应商选择决策和订货批量决策。供应网络的可靠性受各个供应商的中断概率影响。供应网络的可靠性要达到期望容忍可靠性。供应商到物流中心的距离影响供应商的货损。在订货量决策时需要考虑到货物损失，构建了非线性规划模型，考虑了采购成本以及在物流中心的存储和处理成本。设计了基于类似冒泡排序的改进差分算法。类似冒泡排序策略和修复策略是算法改进的关键点。修复策略包括边界条件修复策略和约束条件修复策略。通过LINGO算法和改进遗传算法的对比仿真实验，验证了算法的可行性和有效性。基于多周期多目标的生鲜农产品供应商选择决策和订货分配决策将成为今后的重点研究内容。