基于改进GM(1,1)模型的螺栓联接残余预紧力预测研究
2021-06-30袁秋炜姚齐水余江鸿
袁秋炜,姚齐水,余江鸿,杨 文
(湖南工业大学 机械工程学院,湖南 株洲 412007)
1 研究背景
螺栓作为常用的紧固件,因其有安装方便、装配便利、紧固牢靠等优点,在轨道交通、核电、航空等领域被广泛应用[1-3]。当螺栓联接处于动态载荷的工况时,其更容易发生松动失效现象,从而导致被连接件的脱离,发生工程事故[4]。
针对螺栓联接松弛的问题,现有文献从机理、影响因素、检测等角度进行了研究。如在机理方面,李志彬[5]通过建立二维轴对称螺栓有限元模型,得出了力和边界在异侧时,可以有效提高螺纹承载力分布的均匀性的结论;O.Vingradov 等[6]通过建立螺栓联接动力学模型,得出高频率振动会造成螺栓松动的结论。杨夏明[7]设计了盲孔螺栓联接结构松动试验的装置,对剪切激励下盲孔螺栓联接的松动行为进行了研究,得出随着螺栓预紧力的增加,螺纹接触界面间越不易发生微观滑移的结论。在影响因素方面,王崴等[8]建立了受侧向激励的螺栓有限元模型,分析了初始预紧力、摩擦系数对螺栓松弛机理的影响;Yang G.Q.等[9]通过螺栓联接的参数化三维有限元模型,分析了不同螺距、不同螺纹数的螺栓联接的力学性能。在检测方面,张姝等[10]提出一种基于深度学习的输电线路螺栓检测系统,该系统能够有效、精确地实现巡检图像中螺栓缺陷的实时检测;艾延廷等[11]提出了螺栓联接接触面非线性阻尼识别公式,通过黏性阻尼比的变化来反映螺栓松动与否。吕佳欣等[12]建立了基于蠕变全应变理论的螺栓联接预紧力松弛预测模型。
国内外学者对于螺栓联接松弛问题的研究,大多是基于大量实验数据基础上进行分析和预测。但轨道交道、航天航空等领域,对可靠性要求非常高,要获得螺栓联接松弛的实验样本非常困难,因此,如何基于少样本对螺栓联接松弛进行预测还鲜有研究。
灰色系统理论因为具有不需要大量实验数据和先验概率分布函数的特点,所以在处理少样本问题方面有较大优势,在不同的经济和工程领域得到了广泛应用[13-17]。本文基于灰色GM(1,1)均值差分模型,从原始数据选取方式和弱化处理两个角度对模型进行优化,提出螺栓联接残余预紧力预测方法,以横向振动工况下的第三轨列车受流器滑板螺栓联接为例,对预测方法进行验证。
2 GM(1,1)预测模型
灰色系统理论以不确定性系统为分析对象,从部分已知信息中提取有价值的信息,实现对系统演化规律的描述和预测,具有建模时所需数据样本较少、计算简单且预测精度较高等特点,在科学研究和工程建设中得到了广泛应用[18]。
GM(1,1)模型是灰色预测的基本模型。其建模方法及处理流程是对原始的数据序列进行累加生成处理,然后对模型求解,得到定量的预测序列值,最后还原处理,得到原始数据的预测数据序列。
GM(1,1)模型有4 种基本模型,分别是原始差分模型(original difference grey model,ODGM)、均值差分模型(even difference grey model,EDGM)、离散差分模型(discrete grey model,DGM)和均值模型(even grey model,EGM)。由于螺栓联接残余预紧力具有上下波动和非指数下降的特点,GM(1,1)均值差分模型对此类数据有较高的预测精度,因此本研究采用均值差分模型(EDGM)进行分析。
2.1 模型表述
设序列X(0)=(x(0)(1),x(0)(2),…,x(0)(n)),
式中x(0)(k)≥0,k=1,2,…,n。
设X(0)的累加数据序列为X(1),
X(1)=(x(1)(1),x(1)(2),…,x(1)(k),…,x(1)(n)),
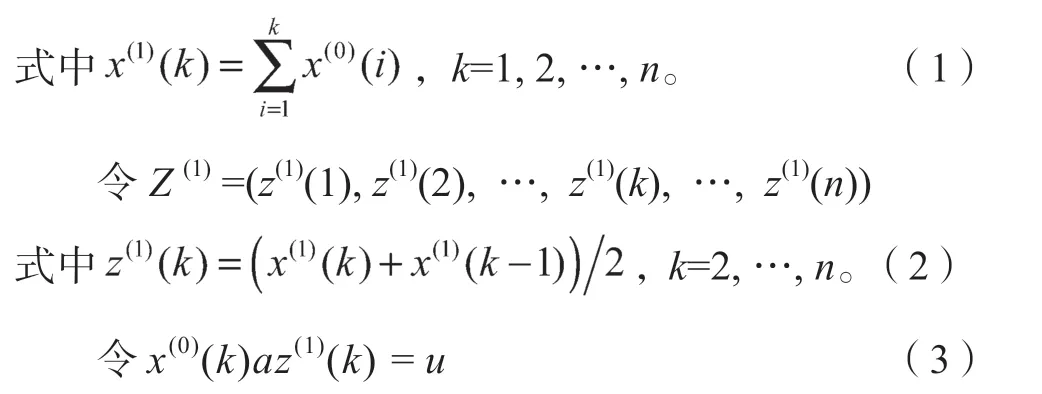
为GM(1,1)模型的原始形式。令-a为发展系数,u为灰色作用量。由式(3)可知,GM(1,1)模型的原始形式本质上是一元差分方程,对于式中-a、u,可以通过最小二乘法进行求解。

式中B、Y分别为

经移项求解得均值差分模型的时间响应函数为

对时间响应函数进行还原处理:

将式(6)和式(7)联立求解可得,

3 螺栓联接残余预紧力预测方法
螺栓联接残余预紧力是评价螺栓联接可靠性的重要参考指标,所以对螺栓联接残余预紧力进行预估和监控,可以有效避免螺栓联接失效所带来的危害。本研究基于改进GM(1,1)均值差分模型对其进行研究,并从原始数据的选取方式和弱化处理两个角度进行优化。
3.1 原始数据的选取
在原始数据的选取方式中,不同的选取方式、不同的GM(1,1)模型,都会导致不同的预测结果。即使同一个GM(1,1)模型,由于原始数据可以选取其中不同部分来分析,求解出的发展系数不同,则其预测结果也会不一致。所以选择合适的原始数据选取方式对于提高预测精度有着重要影响。
随着时间序列的增加,旧数据对于系统行为的影响越来越小。随着新数据的补充,需要去除旧数据,这样选取的分析数据序列才更能反映未来系统行为的 发展趋势。特别是,当系统发生质变,与旧系统的行为发生较大变化时,旧数据淘汰并补充新数据,是最合理的数据选取方法,且此种选取方式也遵循灰色理论的新信息优先原则。另外,在新数据补充的同时,将旧数据淘汰,可以保证数据总量基本不变,从而避免数据过多、计算量过大、计算速度和模拟效率下降等问题。
令未补充新数据,只有旧数据的GM(1,1)模型为原始模型;令补充新数据,淘汰旧数据的GM(1,1)模型为新陈代谢模型;令补充新数据,同时保留旧数据的GM(1,1)模型为新数据模型。现举例计算,对上述3 种模型进行误差比较。
设现有数据序列X(0)=(60.70,73.80,86.20,100.40,123.30)。补充的新数据x(0)(6)=149.50。
1)原始模型模拟预测
由原始分析数据X(0)=(60.70,73.80,86.20,100.40,123.30),使用最小二乘法,根据式(6),可得发展系数-a为0.17,灰色作用量u为55.89。根据式(9),可得原始模型预测的模拟值和误差值,见表1。
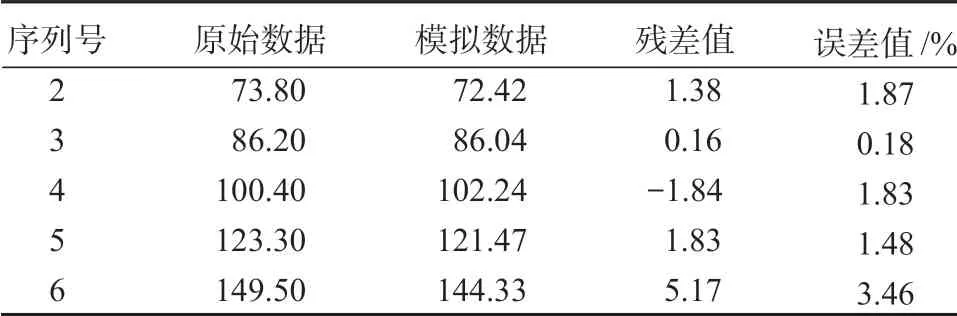
表1 原始模型计算下数据对比及误差值Table 1 Data comparison and error value with original model calculation
2)新数据模型模拟预测
由原始分析数据X(0)=(60.70,73.80,86.20,100.40,123.30,149.50),可得新数据模型预测的模拟值和误差值,如表2所示。
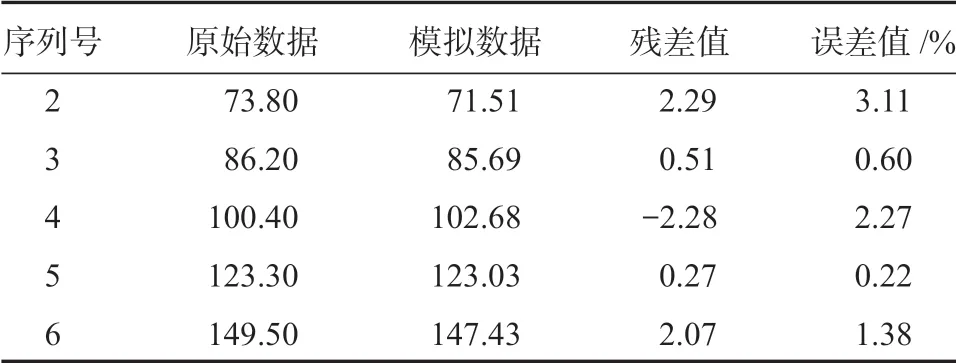
表2 新数据模型计算下数据对比及误差值Table 2 Data comparison and error value with new data model calculation
3)新陈代谢模型模拟预测
由原始分析数据X(0)=(73.80,86.20,100.40,123.30,149.50),得新陈代谢模型预测的模拟值和误差值,见表3。
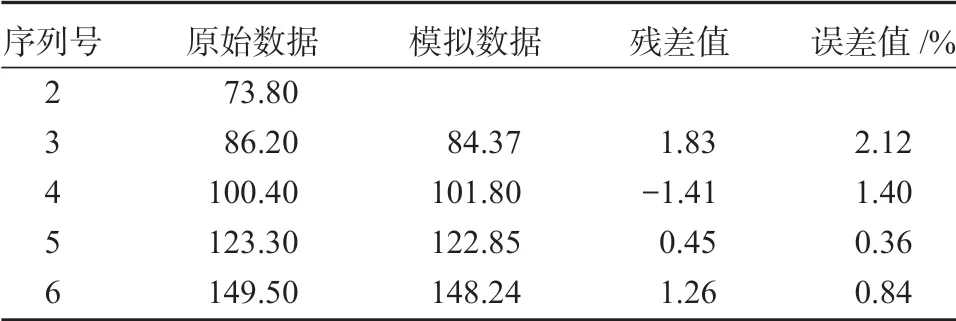
表3 新陈代谢模型计算下数据对比及误差值Table 3 Data comparison and error table with metabolism model calculation
3)3 种模型结果对比
上述3 种模型的预测值和误差值对比结果如表4所示。
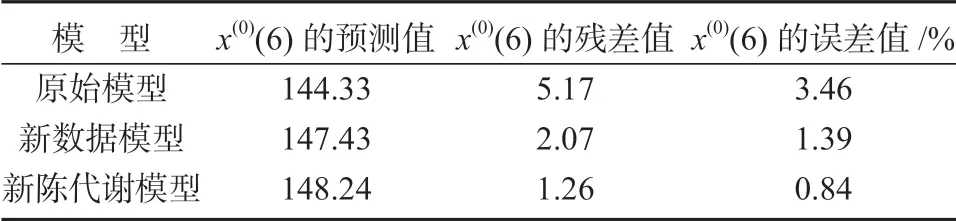
表4 3 种模型的参数、预测值和误差值对比Table 4 Comparison of parameters,predicted values and errors of under three models
由表4 可知,新陈代谢模型在x(0)(6)的预测准确性方面,其残差值和误差值均最小。所以螺栓联接残余预紧力的原始数据选取方式选用新陈代谢方式更为合理。
3.2 原始数据的弱化处理
选取合适的残余预紧力值作为原始数据。针对螺栓联接残余预紧力振荡浮动和前期衰减剧烈的特点,在直接生成累加数据序列之前,对原始分析数据进行多阶弱化处理。
多阶弱化处理属于缓冲算子处理的概念,其核心是不动点定理,即最新数据点经过计算后保持不变。当多阶弱化算子计算单调递减数据序列时,整体模拟的数据值会变大,因此数据序列的减小速率也变缓慢。由于多阶弱化处理使得分析数据序列变得平缓,且遵循新信息优先原则,能有效地减少奇异值对数据分析的影响。所以在对第三轨受流器滑板螺栓联接残余预紧力的原始数据累加生成前,对其进行一阶弱化处理和二阶弱化处理,与未多阶弱化处理的数据一同模拟分析,并对其结果进行比对,找到对螺栓联接残余预紧力数据序列合适的弱化处理阶数。
设原始数据
X(0)=(x(0)(1),x(0)(2),…,x(0)(k),…,x(0)(n)),
式中x(0)(k)≥0,k=2,…,n。
对X(0)进行一阶弱化处理,令
X′(0)=(x(0)(1)d,x(0)(2)d,…,x(0)(k)d,…,x(0)(n)d),
式中

则X′(0)为一阶弱化处理后的数据序列。而二阶弱化处理,是对一阶弱化处理后的数据序列X′(0)再进行一次弱化处理。
4 算例分析
4.1 螺栓残余预紧力值的测量
数控横向振动试验台由传感器、夹紧装置、拧紧装置等零部件组成,如图1所示。数控横向振动试验台可以通过传感器实时测量螺栓的残余预紧力。受测螺栓为第三轨列车受流器滑板螺栓联接中常用的型号,公称直径为14 cm。

图1 数控横向振动试验台Fig.Numerical control transverse vibration test bed
4.2 螺栓联接残余预紧力预测方法的验证
选取螺栓振动初期的残余预紧力变化,作为模拟预测对象,以确定螺栓联接GM(1,1)模型的有效性。
1)选取分析数据
根据所测的实验数据,选取残余预紧力值为分析数据,单位为N。以下因为只分析数据的数值大小,故将单位省略。设原始模型选取的数据序列X(0)=(23 925.50,20 660.00,20 287.00,20 170.00,19 959.00,19 896.00,19 819.00,19 765.50),令新数据模型选取的序列为X(1)=(23 925.50,20 660.00,20 287.00,20 170.00,19 959.00,19 896.00,19 819.000,19 765.50,19 759.00),令新陈代谢模型选取的数据序列令为X(2)=(20 660.00,20 287.00,20 170.00,19 959.00,19 896.00,19 819.00,19 765.50,19 759.00)。
对X(0)、X(1)和X(2)分别进行累加,得到对应的累加序列,并经过模拟计算,分别得到其模拟数据、残差值和误差值表,见表5~7。
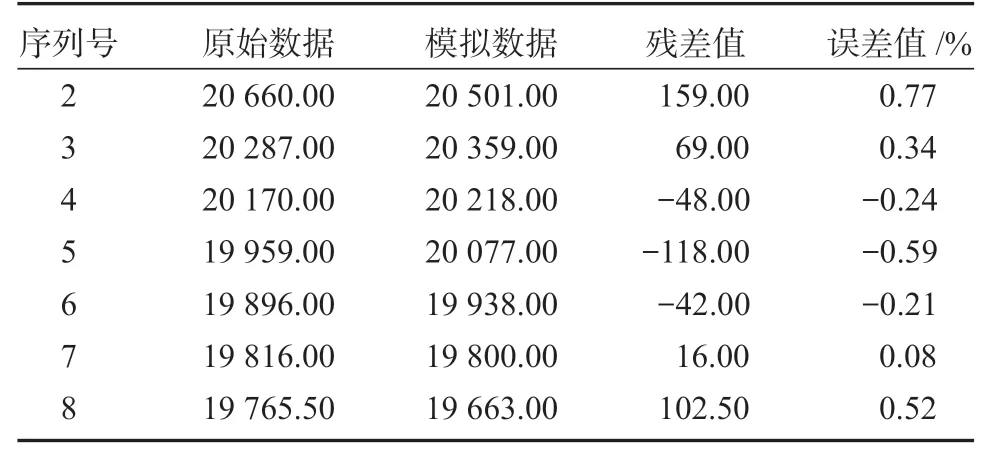
表5 原始模型计算下的数据对比及误差值Table 5 Data comparison and error value with original model calculation
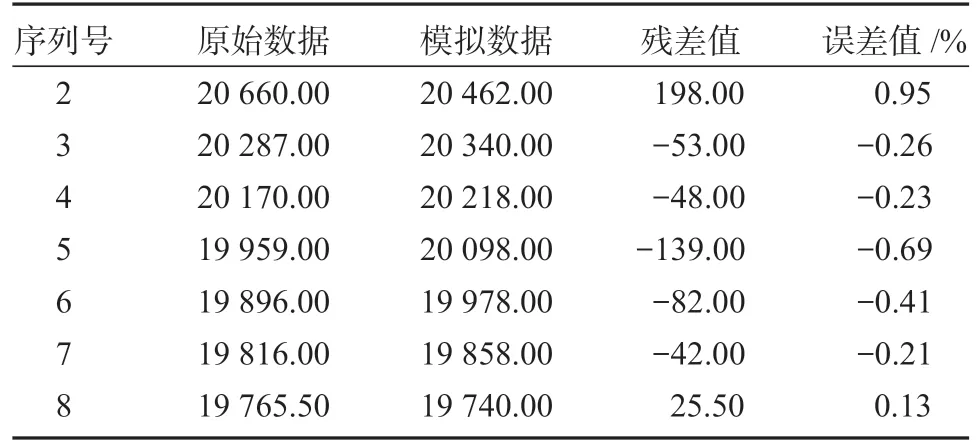
表6 新数据模型计算下的数据对比及误差值Table 6 Data comparison and error value with new data model calculation
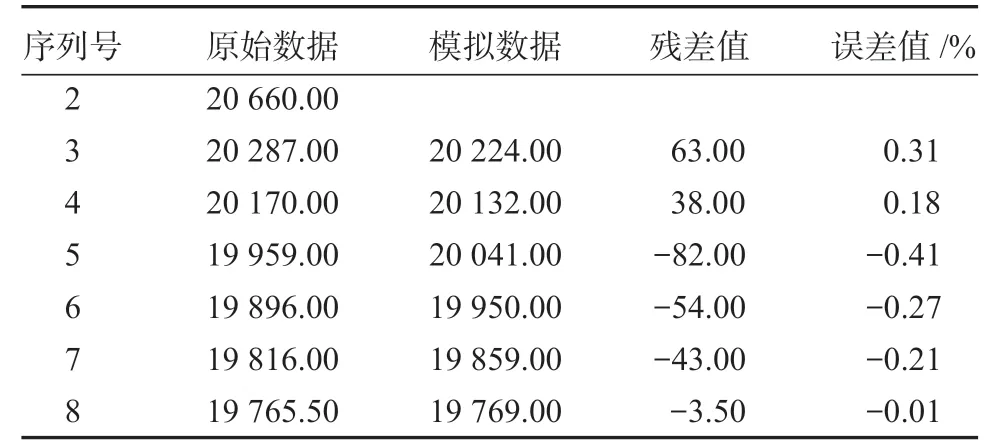
表7 新陈代谢模型计算下的数据对比及误差值Table 7 Data comparison and error value with metabolism model calculation
3 种模型的预测值和误差值对比见表8。
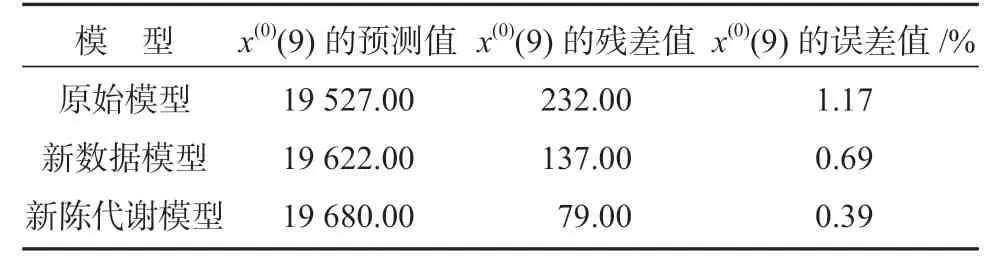
表8 3 种模型的预测值和误差对比Table 8 Comparison of predicted values and errors under three models
由表8 可知,新陈代谢模型在预测残差值和误差值方面,均优于另外两个模型的,所以螺栓联接残余预紧力预测方法的选取使用新陈代谢模拟可以更好地提高预测精度。
2)弱化处理阶数
设原始分析数据序列X(0)=(23 925.50,20 660.00,20 287.00,20 170.00,19 959.00,19 896.00,19 819.00,19 765.50)。经过计算,得其一阶弱化处理数据序列为X′(0)=(20 560.00,20 079.00,19 983.00,19 922.00,19 860.00,19 827.00,19 792.00,19 765.50),二阶弱化处理数据序列为X″(0)=(19 973.60,19 889.80,19 858.20,19 833.30,19 811.10,19 794.90,19 778.90,19 765.50)。对3 种分析数据,通过均值差分GM(1,1)模型进行模拟预测。3种模型的发展系数、预测值和误差对比结果如表9所示。

表9 3 种模型的参数、预测值和误差对比Table 9 Comparison of parameters,predicted values and errors of the three models
根据表9 可知,对数据进行一阶和二阶弱化处理,使得预测准确度有了明显改善,故在对螺栓联接残余预紧力进行预测时,需要对分析数据进行弱化处理,以提高其预测精度。
4.3 螺栓联接残余预紧力预测方法的模拟预测
根据螺栓联接残余预紧力预测方法,对螺栓联接的残余预紧力进行模拟预测。为了减少计算量,加快计算速度,对实验数据进行等间隔选取。设原始数据序列X(0)=(23 925.50,19 566.50,19 369.00,19 115.00,18 955.00,18 797.50,18 703.00,18 578.00,18 563.00,18 424.00,18 412.00)。为验证模型,课题组选取前8 个数据为分析数据,后3 个数据为对比数据。则原始分析数据序列X(0)=(23 925.50,19 566.50,19 369.00,19 115.00,18 955.00,18 797.50,18 703.00,18 578.00)。经计算,得出一阶弱化处理数据序列X′(0)=(19 626.00,19 012.00,18 919.70,18 830.00,18 758.60,18 693.00,18 641.00,18 578.00),二阶弱化处理数据序列X″(0)=(18 882.00,18 776.00,18 736.80,18 700.00,18 667.80,18 637.50,18 609.70,18 578.00)。通过螺栓联接均值GM(1,1)模型进行计算分析,得到的模拟预测值,如图2所示。
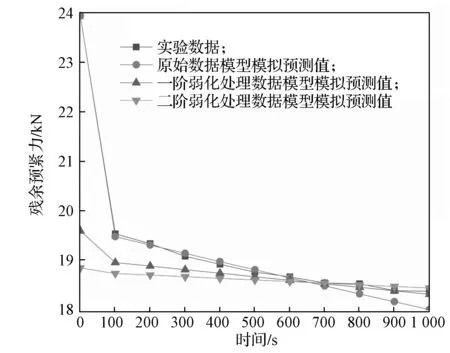
图2 不同处理数据方法的残余预紧力变化曲线Fig.2 Variation curves of residual preload with different data processing methods
由图2 可知,原始数据模型对已知数据的模拟值,与真实值间的误差较小。但其预测值的误差随着振动时间的增加,相较于其他两个模型明显变大。所以在预测值方面,弱化处理模型的精度更加准确。3 种模型在预测值方面的误差值见表10。

表10 3 种模型的参数、预测值和误差对比Table 10 Comparison of parameters,predicted values and errors of the three models
由表10 可知3 种模型对于3 个预测值的平均相对误差分别为1.72%,0.24%,0.31%。对于螺栓联接GM(1,1)模型而言,对数据进行一阶弱化处理比二阶弱化处理的模型精度高。根据螺栓联接残余预紧力预测方法对螺栓联接残余预紧力进行预测,验证了螺栓联接残余预紧力预测方法的可靠性。
5 结论
1)当螺栓联接处于横向振动工况时,通过新陈代谢的方法选取残余预紧力数据序列,作为原始数据,能减小螺栓联接残余预紧力预测方法的误差;
2)对螺栓联接残余预紧力数据,进行弱化处理,尤其是一阶弱化处理,能有效地提高螺栓联接残余预紧力预测方法的准确性;
3)根据螺栓联接残余预紧力预测方法对算例中螺栓联接残余预紧力进行预测,验证了螺栓联接残余预紧力预测方法的可靠性。
