密实度对粗粒料力学特性影响三轴试验研究

朱材峰，朱俊高*，潘 政

(1. 河海大学 岩土力学与堤坝工程教育部重点实验室，江苏 南京 210098；2. 四川电力设计咨询有限责任公司，四川 成都 610016)

粗粒料粒径范围广，排列方式复杂，存在颗粒破碎效应及剪胀效应，具有极为复杂的力学性质[1]。影响粗粒料力学性质的因素有很多，比如相对密实度、颗粒级配、应力历史、加载条件、应力路径等，其中相对密实度是重要因素之一。密实度同时也是土石坝等填方工程设计时重要控制指标之一，选取不当会影响工程的经济性及安全性，所以探讨相对密实度与土体力学性质之间的关系是非常必要的。

姜景山等[2]利用大型真三轴试验得出密度和围压是影响粗粒土力学性质的重要因素；徐日庆等[3]针对两种级配不同的福建标准干砂，着重探讨了不同初始相对密实度对砂土抗剪强度的影响；李振等[4]通过对同一级配的河床砂卵石在不同相对密度下进行直接剪切试验得出：抗剪强度参数随着干密度的增大而增大，最终有趋于某一稳定值的趋势；陈铖等[5]采用三维颗粒流软件PFC3D模拟研究了5种不同级配下粗粒土在3种不同围压下的变形特性；凌华等[6]通过大型三轴排水剪切试验研究了级配对粗粒土强度、变形、剪胀特性和颗粒破碎的影响，试验结果表明细颗粒含量的大小、是否含泥是粗粒土力学特性的重要影响因素；姜景山等[7]通过大型三轴压缩试验得出密度是决定粗粒土初始弹性模量的根本因素, 而剪切变形过程中弹性模量则是密度和应力状态共同决定的；王俊杰等[8]通过室内试验研究发现粗粒土的渗透系数随着密实度的增加而逐渐减小。虽然前人已经研究了相对密实度对土体力学性质的影响，但是对粗粒料相关方面的研究不够系统全面。

因此，本文基于前人的研究经验[9-12]，通过对某大坝粗粒料进行不同相对密实度下的常规三轴试验，探究不同相对密实度对粗粒料应力应变特性和强度特性的影响，为土石坝工程实践提供一定的借鉴。

1 试验土料与试验方案

1.1 试验土料

本次试验土料选用某大坝地基覆盖层料(为砂卵砾石料)，属于无粘性粗粒料。由筛分试验可知覆盖层料最大粒径为100 mm，而常规中型三轴仪容许试样最大粒径为20 mm，故通过等量替代法[13-14]对原土料进行缩尺得到试验替代料级配，原级配和试验替代料的级配曲线如图1所示。采用震动台法测得试验土料的最大干密度为2.30 g/cm3，由松填法测得试验土料的最小干密度为1.93 g/cm3。

图1 原土料和试验替代料的级配曲线Fig.1 Gradation graph of original soil material and test substitute

1.2 试验方案

本文试验在中型三轴仪(图2(a))上进行，试样直径为101 mm，高为200 mm。试验为固结排水剪(CD)，试样的相对密实度Dr设计为0.7、0.8、0.9。每种相对密实度制备4个试样，制样时按等量替代法缩尺的级配比例算出每个粒径范围内所需要的粗粒料的质量，然后分5层击实，固结时间为1 h，受剪前试样如图2(b)所示。对同一相对密实度下的4个试样分别施加200、400、800、1 200 kPa的围压。

图2 试验仪器和试样Fig.2 Test equipment and samples

对于本文试验所用的无粘性粗粒料来说，剪切过程中孔隙水压力易消散，抗剪强度基本不受剪切速率的影响，故剪切速率取0.25 mm/min，剪切至30 mm终止。

2 试验结果分析

2.1 应力应变特性分析

试验结束后的受剪试样如图3所示，图4至图7给出了不同围压下不同相对密实度的应力应变关系曲线，由图可得：试样的应力应变曲线均表现为软化型，对于相对密度为0.7的试样，在受剪初期，随轴向应变的增加，应力逐渐上升到峰值后开始缓慢降低，在受剪后期，曲线出现水平段，应力趋于一恒定值，通常将这一恒定的强度称为残余强度，这与密实砂土所表现出来的应力应变特性很相似[15]。对于相对密实度为0.8、0.9的试样，应力达到峰值后，应力大小并没有立即下降，而是出现长度不等的水平段，应力值变化在5%以内，此时试样仍具有较大的强度，特别在高围压时表现得较为明显。

图3 受剪后试样Fig.3 Sample after shearing

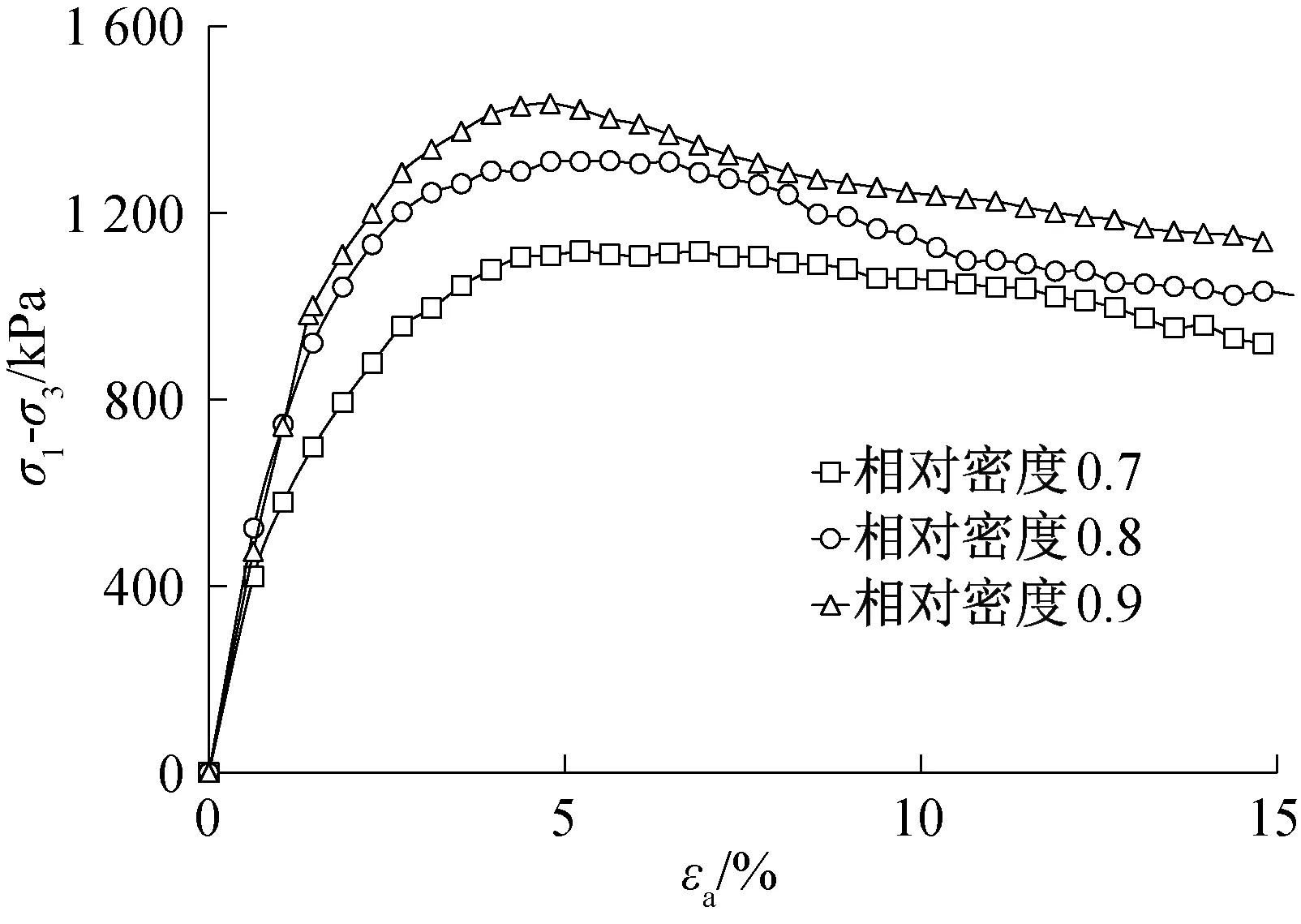
图4 200 kPa围压下不同相对密实度(σ1-σ3)-εa关系曲线Fig.4 (σ1-σ3)-εa curves of different relative density under 200 kPa confining pressure

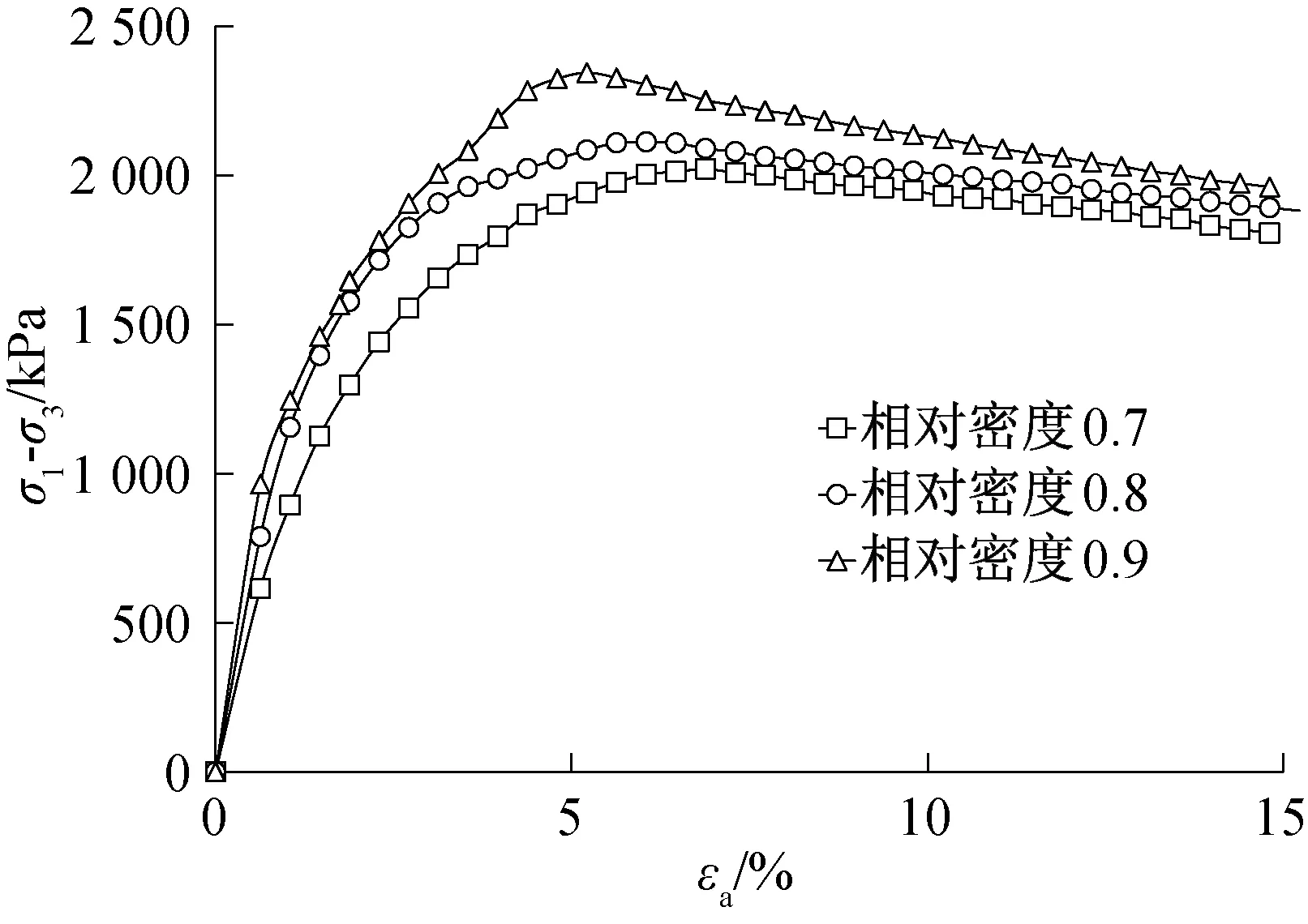
图5 400 kPa围压下不同相对密实度(σ1-σ3)-εa关系曲线Fig.5 (σ1-σ3)-εa curves of different relative density under 400 kPa confining pressure

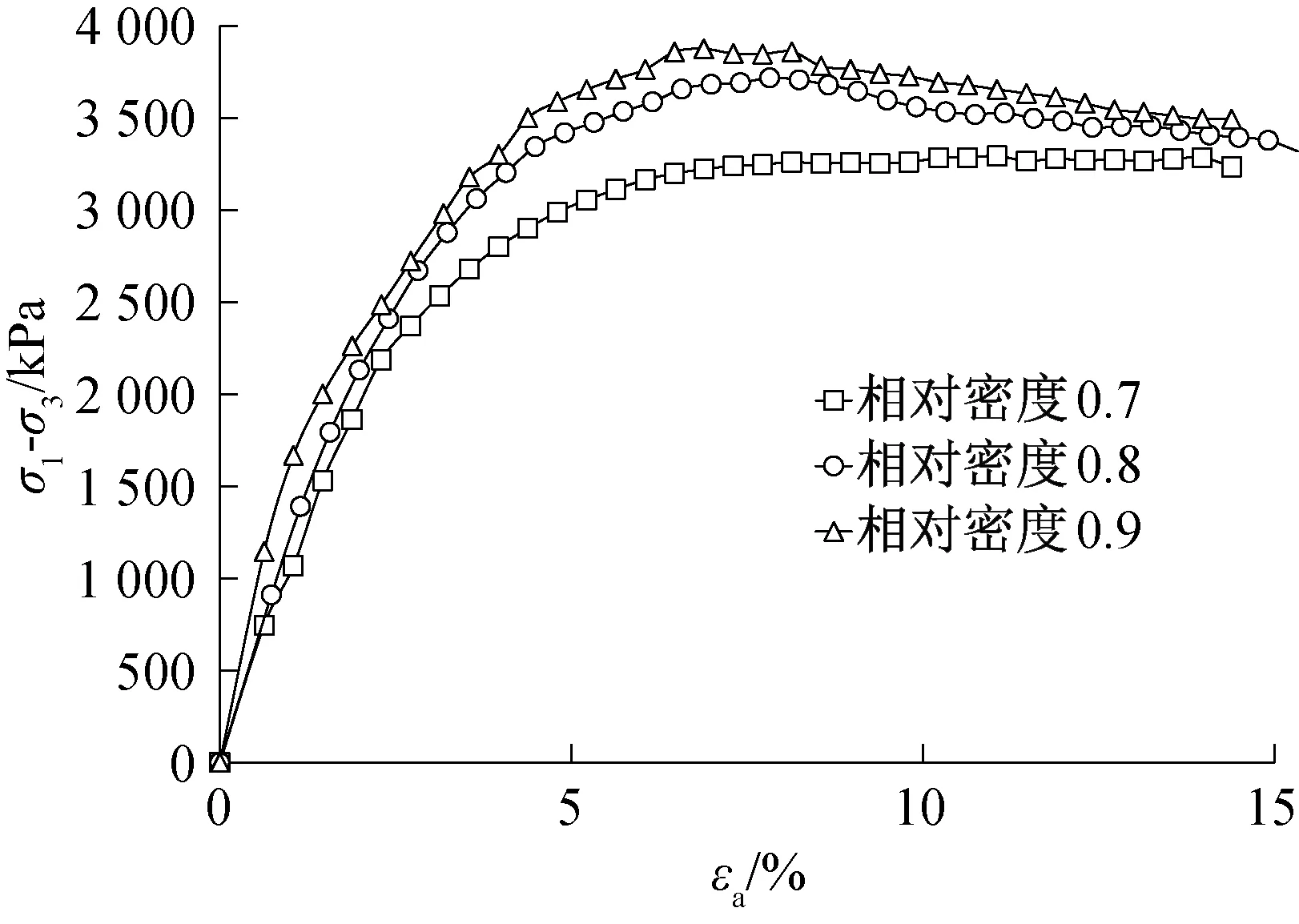
图6 800 kPa围压下不同相对密实度(σ1-σ3)-εa关系曲线Fig.6 (σ1-σ3)-εa curves of different relative density under 800 kPa confining pressure

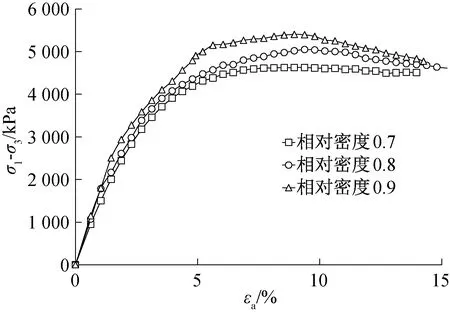
图7 1 200 kPa围压下不同相对密实度(σ1-σ3)-εa关系曲线Fig.7 (σ1-σ3)-εa curves of different relative density under 1 200 kPa confining pressure

之所以出现上述现象，是由于当制样密度较大，围压较大时，在受剪初始阶段，颗粒间接触紧密，剪力较小，不足以引起颗粒破碎以及颗粒间的相对移动，变形以弹性为主，随着剪力的不断增加，当剪力大于颗粒间接触力时，一部分颗粒有滚过其他颗粒而产生相对错动的趋势，此时必须要克服较大的咬合作用力，所以表现出较高的抗剪强度；而且当剪力超过颗粒本身强度时，颗粒间点接触的尖角部位发生断裂破碎，产生了细颗粒，进一步充填了原来的孔隙，使得结构更加紧密，因此仍然能够承担较大的剪力。

试样在不同相对密实度不同围压下的峰值强度如表1所示，从表1可以看出同一相对密实度下试样所受的围压越大，所表现出的峰值强度就越大，峰值强度越迟出现；同一围压下，试样的相对密实度越大，所表现出的峰值强度也越大，峰值强度越早到达。

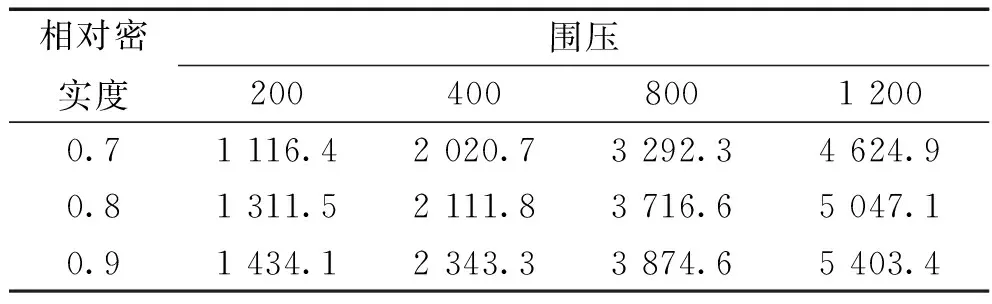
表1 不同相对密实度不同围压下的峰值强度(单位：kPa)

这是由于相对密实度大的试样，颗粒之间填充密实，剪切初期，颗粒之间没有相互移动，一部分颗粒要滚过另一部分颗粒才能产生较大错动，而相对密实度小的试样，颗粒之间本身处于松散状态，剪切初期颗粒之间的密实程度不断提高，所以，在相同的围压下相对密实度大的试样更早达到峰值强度，而相对密实度小的试样有一段时间是处于颗粒重新排列变密实的过程，峰值强度会出现的晚一些。

由图4至图7还可以看出：在同一围压下，相对密实度对应力应变曲线的形态影响较大，在达到峰值强度以前，应力应变曲线形态均随相对密实度的增加而变“陡”，即曲线初始斜率变大，初始切线模量Ei增大；在达到峰值强度以后，曲线表现出更加明显的软化现象。

Janbu[16]的研究发现，对于土体而言，初始切线模量Ei与围压近似表现出幂函数关系，具体可以表示为：

(1)

式中K和n为邓肯-张模型参数，pa为大气压力，依此关系求得不同相对密实度下邓肯-张模型参数Rf、n和K的值，如表2所示。

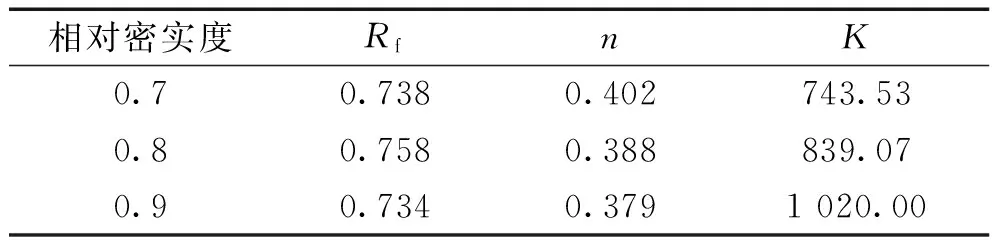
表2 不同相对密实度下邓肯-张模型参数Rf、n和K

由表2可得，随相对密实度的增大，参数Rf和n均仅在0.03左右内波动，几乎不受相对密实度的影响，如图8(a)所示；参数K与相对密实度之间呈现出较好的线性关系，如图8(b)所示，所以，参数K随密实度Dr的变化可以近似用下式表示：

K=a1Dr+d1

(2)

式中，参数a1、b1分别为1 980.7、-747.2。

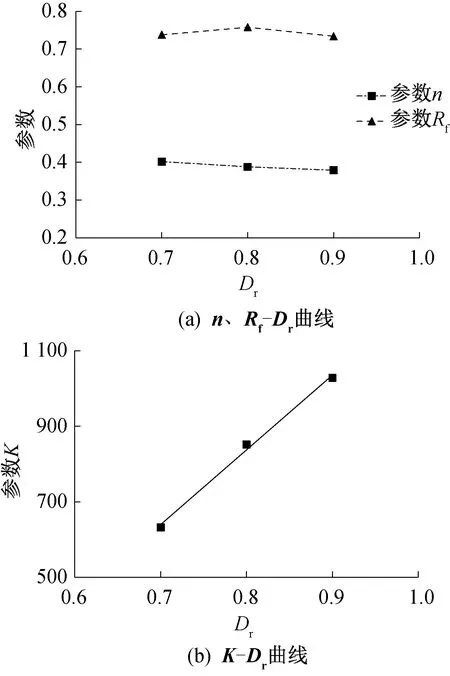
图8 邓肯-张模型参数与相对密实度Dr关系Fig.8 Relationship curves between Duncan Chang model parameters and Dr

应变软化是粗粒料的一个重要特性。软化程度除了与颗粒自身岩性有关外，主要与密实程度和围压有关。要在本构模型中准确反映粗粒料的软化特性，必须对其软化规律有清楚的了解[17]。为此，作者对本文试验粗粒料的软化性质进行了深入研究。

为了表示应力应变曲线的软化现象，现引入参数λ，定义为粗粒料应力应变曲线的软化系数，软化系数λ由式(3)求得：

(3)

式中(σ1-σ3)f为峰值强度如表1所示，(σ1-σ3)r为残余偏应力如表3所示。

绘制出软化系数λ和lg (σ3/pa)的关系曲线如图9(a)所示，图9(a)显示，同一Dr对应不同lg (σ3/pa)的4个点可近似用直线拟合，设λ-lg (σ3/pa)拟合直线的斜率和截距分别为α和ψ，整理发现，不同Dr时的斜率α相差不大，截距ψ随相对密实度Dr变化也表现出比较好的线性关系，如图9(b)所示。遂对斜率α取平均值为-1.27，利用α和ψ-Dr的关系来进行直线拟合。可以得出，参数λ随着围压σ3和密实度Dr的变化可以用式(4)表示：

(4)

式中α，β，δ为拟合参数，对于试验所用的粗粒料，分别等于-1.27，2.50，-0.42。

图9 软化系数λ与围压和相对密实度的关系曲线Fig.9 Relationship curves between λ and Dr

式(4)是根据此次试验数据归纳总结出来的，由于实验数据比较有限，因此存在一定的局限性，还需要更多的试验数据来验证其适用性。

2.2 体积变形特性分析

图10至图13给出不同围压下不同相对密实度的体积应变和轴向应变关系曲线，从图中可以看出，在同一围压下，随着相对密实度的增大，试样的剪胀性逐渐变强，在εv-εa曲线上表现为对应相同的轴向应变εa，相对密实度大的试样曲线对应的体积应变εv更小。在同一相对密实度下，随着围压的增大，试样的剪胀性逐渐减弱，在εv-εa曲线上表现为对应相同的轴向应变εa，围压大的试样曲线对应的体积应变εv更大，特别是在围压为1 200 kPa时，试样最终表现出来的体积变形都为剪缩。

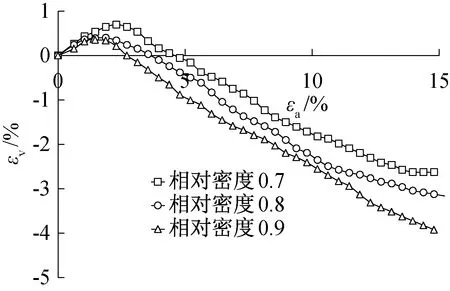
图10 200 kPa围压下不同相对密实度εv-εa关系曲线Fig.10 εv-εa curves of different relative density under 200 kPa confining pressure

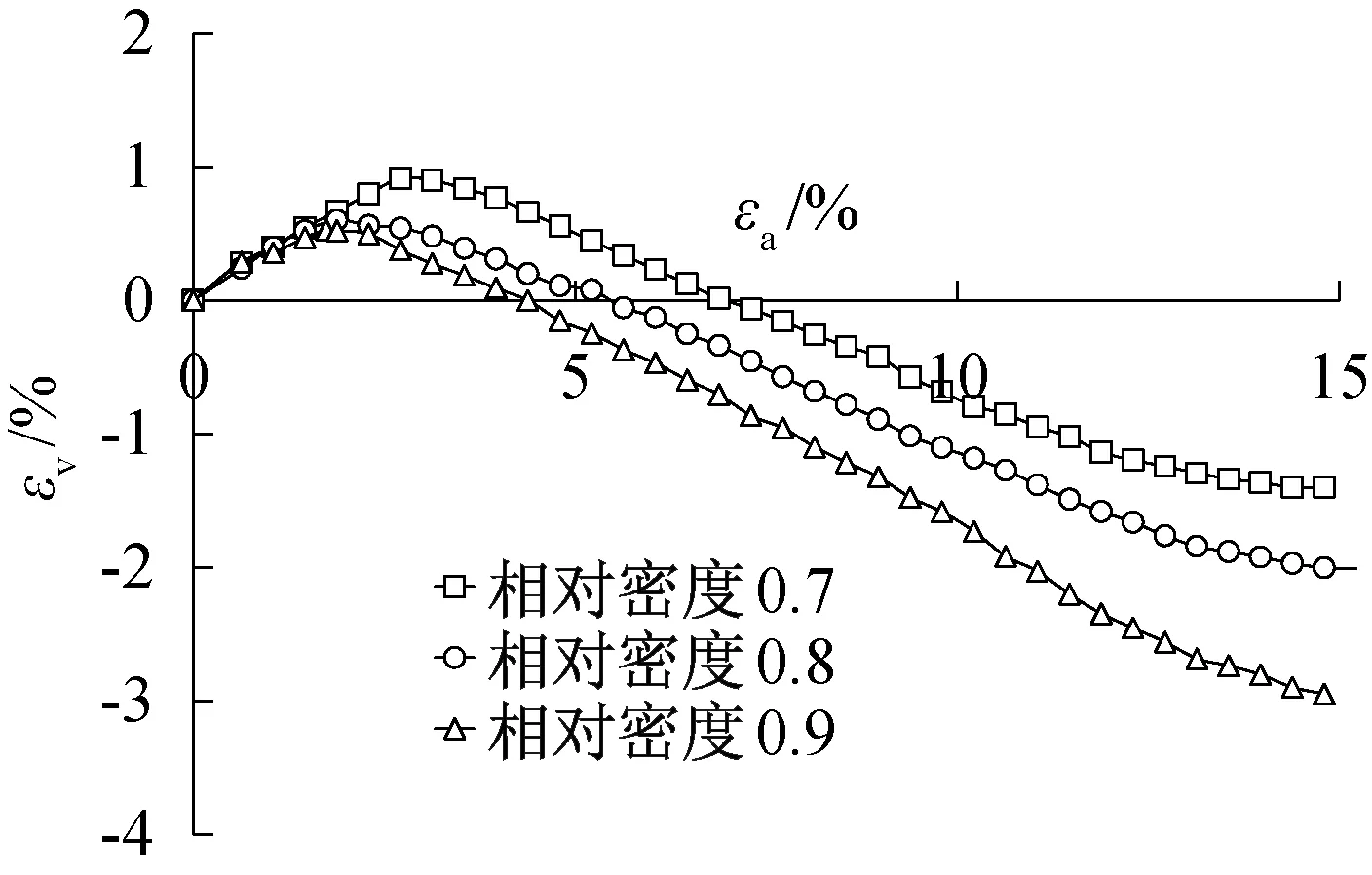
图11 400 kPa围压下不同相对密实度εv-εa关系曲线Fig.11 εv-εa curves of different relative density under 400 kPa confining pressure

图12 800 kPa围压下不同相对密实度εv-εa关系曲线Fig.12 εv-εa curves of different relative density under 800 kPa confining pressure

图13 1 200 kPa围压下不同相对密实度εv-εa关系曲线Fig.13 εv-εa curves of different relative density under 1 200 kPa confining pressure

2.3 强度特性分析

为了分析相对密实度对试样破坏时偏应力的影响，整理得出试样破坏偏应力比(σ1-σ3)f/σ3。发现在同一围压下，破坏偏应力比(σ1-σ3)f/σ3与相对密实度Dr成正相关；当围压σ3分别为200、400、800、1 200 kPa时，相对密实度Dr每增大0.1，破坏偏应力比平均相应增加0.794、0.403、0.364、0.324，可以看出当围压增大到一定值时，相对密实度对破坏偏应力比的影响越来越小，原因可能是高围压导致了粗粒料颗粒的破碎，间接地增大了粗粒料的密实度。

表3整理了不同相对密实度试样破坏时的残余偏应力(σ1-σ3)r，这里认定残余偏应力是指试样在某个围压下剪切至最大应变时的偏应力。

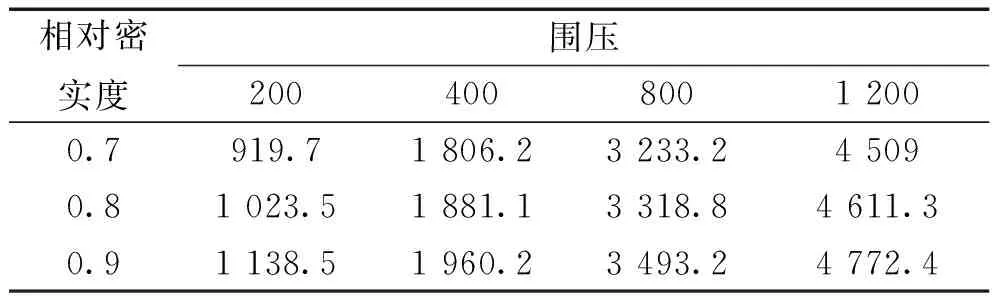
表3 不同相对密实度试样破坏时的残余偏应力(单位：kPa)

从表3可以看出，不同相对密实度试样的最终残余偏应力基本上都很接近。对同一围压下的残余偏应力求其平均值，用qr表示；同时整理出相对偏差值|(σ1-σ3)r-qr|/qr，用R来表示，如表4所示，除了在200 kPa、Dr=0.7以及200 kPa、Dr=0.9时，R有点大以外，其余点的相对偏差值都小于5%。将不同围压下的R求平均值，得出结果为3.72%。由此可见，相对密实度对残余偏应力或残余强度影响较小。

表4 不同相对密实度试样残余偏应力相对偏差R(%)

依据试验结果，进一步整理出三种不同相对密实度试样进行固结排水剪切试验得到的抗剪强度指标列于表5中。

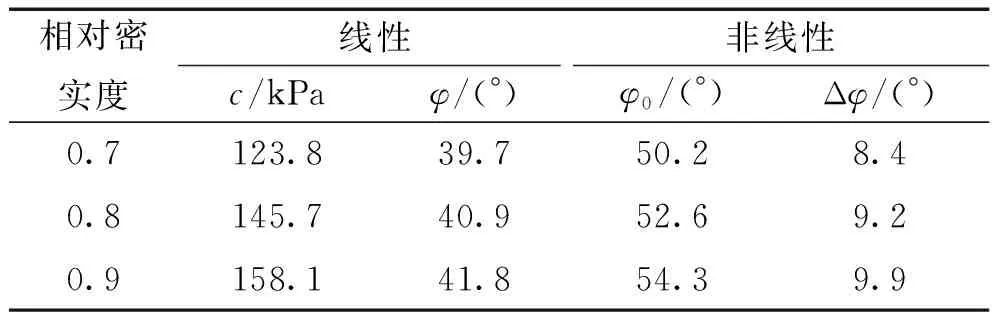
表5 不同相对密实度试样三轴固结排水剪切试验强度指标

由表5数据可知，随着相对密实度Dr的增大，不论是线性强度参数还是非线性强度参数都是增大的，而且相对密实度和强度参数之间表现出较好的变化规律，可以近似用直线进行拟合，关系式为：

c=f1Dr+g1

(5)

φ=f2Dr+g2

(6)

φ0=f3Dr+g3

(7)

Δφ=f4Dr+g4

(8)

式中f1，f2，f3，f4和g1，g2，g3，g4为拟合参数，分别为17.15，1.05，2.05，0.75和108.23，38.70，48.27，7.67。用线性函数式(5)到式(8)拟合的结果如图14和图15所示。

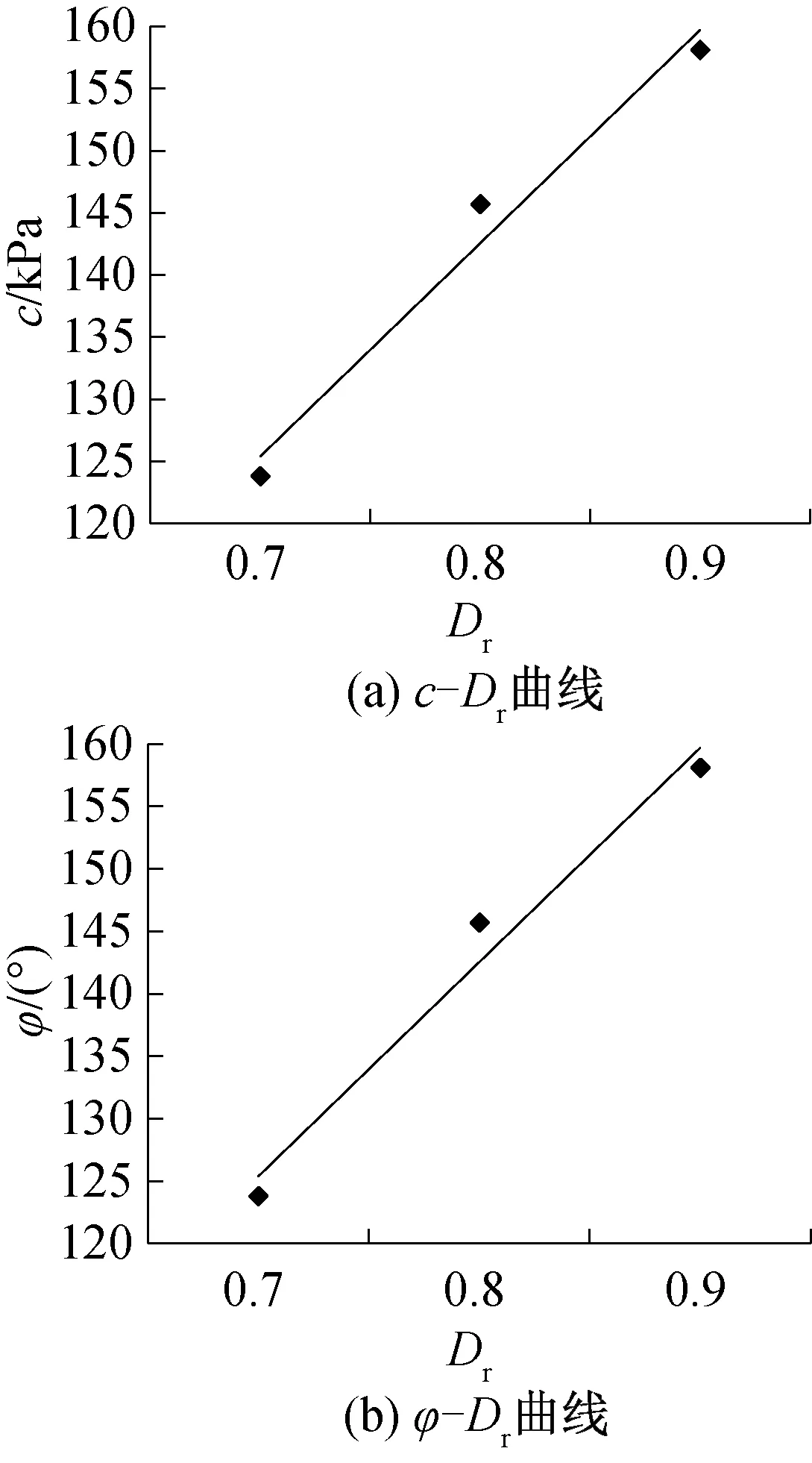
图14 线性强度参数与Dr的关系曲线Fig.14 Relation curve between linear strength parameters and Dr

图15 非线性强度参数与Dr的关系曲线Fig.15 Relation curve between nonlinear strength parameters and Dr

从图14和图15可以看出不论是采用线性强度参数，还是采用粘聚力等于零的非线性强度参数进行拟合，得出来的曲线拟合程度都很高，计算得出后者拟合曲线的R2分别为0.990 4和0.998 5，可以看出采用非线性强度参数与相对密实度Dr拟合的效果更好，原因可能在于土体在高围压下存在颗粒破碎的现象，土体的强度包线往往表现出向下弯的趋势，而不再是一条直线。

通过研究非线性强度指标值φ0、Δφ与相对密实度Dr呈现出的线性关系，如果能够测得覆盖层粗粒料的现场干密实度或换算出相对密实度，则根据此线性关系能够推得现场土料的非线性强度指标，这对于在实际工程中确定土体强度具有重要的参考价值。

3 结论

本文通过对某大坝覆盖层粗粒料制作试验替代料并进行不同相对密实度下的常规三轴试验，研究了不同相对密实度对粗粒料应力应变和强度特性的影响，主要得出以下结论：

1)同一相对密实度下，随着围压的增加，软化现象更加明显，峰值强度随之增加，出现强度峰值时的轴向应变值也逐渐增加；同一围压下，随着相对密实度的增加，峰值强度也逐渐变大，但是出现强度峰值时的轴向应变值反而逐渐减小。

2)在同一围压下，随着相对密实度的增大，曲线表现出更加明显的软化现象，初始切线模量Ei逐渐增大。邓肯模型参数Rf和n基本不受相对密实度的扰动，参数K与相对密实度近似呈线性变化规律；引入了新的参数软化系数λ，建立了软化系数λ与围压和相对密实度的关系式，可作为反映试验粗粒料软化特性规律的参考。

3)在同一围压下，随着相对密实度的增大，试样的剪胀性逐渐增强；在同一相对密实度下，随着围压的增大，试样的剪胀性逐渐减弱，特别在围压为1 200 kPa时，试样最终表现出来的体积变形都为剪缩。

4)相对密实度和围压对试样破坏时的偏应力影响较大，试样的残余强度受相对密实度的影响较小。当围压分别为200、400、800、1 200 kPa时，相对密实度Dr每增大0.1，破坏偏应力比平均相应增加0.794、0.403、0.364、0.324。

5)线性强度参数和非线性强度参数均随相对密实度Dr的增大而增大；其中采用非线性强度参数与相对密实度Dr拟合的效果更好，可依此线性关系推得现场粗粒料的非线性强度指标，以为实际工程中确定强度参数提供参考。