移位安全区约束下的建筑物群移位免疫遗传算法

刘远刚，李少华，蔡永香，何贞铭,马潇雅，李鹏程，郭庆胜，何宗宜,

1. 长江大学地球科学学院，湖北 武汉 430100； 2. 武汉大学资源与环境科学学院, 湖北 武汉 430079

地图综合是为了适应地图比例尺和制图目标等条件而进行的一种地理信息提取与抽象过程[1]。地图综合过程中，由于比例尺缩小，不可避免地产生空间冲突。为了保持地图清晰性，需要采用空间上下文相关的地图综合操作对各种冲突进行处理。移位是解决地图目标之间邻近冲突最常用的操作之一[2]。该操作通过调整地图目标的位置解决由于地图符号重叠或靠得太近而导致的图形冲突。

建筑物是普通地图和专题地图中一种重要的人文要素，建筑物群内部以及建筑物与邻近街道之间邻近冲突解决是移位算法研究的重点[3-5]。针对建筑物群的移位问题，国内外学者提出了两类最优化算法，即函数最优化算法和组合最优化算法[6]。前者将物理、数学、工程科学领域已经得到广泛应用的各种模型用于模拟地图综合中的移位问题的机理，从而建立能够考虑多种约束条件的移位数学方程式[7-11]；后者借鉴地图注记自动配置的思路，将建筑物群移位问题视为一种排列组合问题，通过图中建筑物位置的大量试探寻找最佳的地图移位方案，在此过程中采用启发式或群智能搜索算法求得最优解或可行解。本文重点关注后者。

文献[12]最早提出组合最优化移位算法，分别采用最大梯度下降法和模拟退火算法对地图上建筑物进行迭代式的移位。作为对模拟退火移位算法的改进，文献[13]进一步提出了同时采用移位、夸大、缩小和删除等多算子协同的冲突处理方法。文献[14]针对大规模建筑物群移位提出了一种遵循“社交适宜距离保持”的最优化移位算法。文献[15]将几何推理和最大梯度下降法相结合，提出了地图目标冲突探测及其最优化处理方法。类似的研究还有基于禁忌搜索的移位算法[16]、基于遗传算法的移位算法[17]、基于免疫遗传算法的移位算法[18]、基于粒子群算法的移位算法[19]、基于多种群遗传算法的移位算法[20]。这类算法借助各种通用最优化算法的普适性，将原本复杂的移位问题模式化，将各制图约束条件量化为一个目标函数，降低了算法设计和求解的难度。然而，与地图要素空间关系和空间分布特征相关的更高层次的制图约束的形式化与计算异常复杂[21]，难以在算法的目标函数中准确而充分地体现，但它们却是地图综合尤其是移位操作须重点关注的空间特征[22]。例如，文献[3,23]利用Voronoi图构建移位场模型，较好地保持了目标群的相对空间关系，同时采用局部群组整体移位的方式保持建筑物群的分布模式；文献[24]将建筑物群的邻近图作为移位几何模型，保持建筑物群的邻近关系和整体结构，并将局部群组聚合为邻近图中的一个结点参与移位，以保持建筑物局部模式。因此，有必要针对移位过程中地图目标的空间关系和空间分布特征保持问题，采用相应的辅助模型或移位策略对最优化算法的约束条件加以补充，以提高算法对移位问题的适用性。

本文基于免疫遗传算法提出一种顾及空间关系和空间分布特征的建筑物群最优化移位算法。该算法将建筑物群的移位问题定义为一个多目标最优化问题，然后采用免疫遗传算法求解。为了尽量保持建筑物群的空间关系和总体分布特征，采用Voronoi图和缓冲区构建每个建筑物的移位安全区，用于限定地图中建筑物的移位空间；同时，采用建筑物群整体移位策略，保持局部分布模式。并在算法实现中引入一系列移位策略，以增强算法对移位问题的适用性。

1 建筑物群移位问题的形式化定义

1.1 相关约束条件

地图综合约束条件是地图综合目标的概念化定义，也是地图综合结果质量评价的依据[25]。建筑物群移位需要考虑的主要约束条件包括“地图表达的清晰性、地图目标几何形状的相似性、空间关系与空间分布特征的一致性、地理位置的精确性”等方面。本文仅对建筑物进行移位操作，不做缩放、变形处理，也不对地图中道路做移位处理，因此不考虑“地图目标几何形状的相似性”，相关约束如下。

(1) 地图表达的清晰性。地图目标之间的距离应该达到制图规范所规定的最小距离要求。例如，在距离目标30 cm时，人眼能分辨的最小间隔距离为0.2 mm[26]。若两个地图目标之间的距离小于最小距离阈值，就产生邻近冲突。前人研究一般以邻近冲突个数作为地图表达的清晰性评价指标，而本文采用文献[27]中定义的冲突严重程度作为其量化指标，此处称之为冲突大小。将整幅地图上所有冲突大小之和作为评价地图清晰性的量化指标，冲突越严重，清晰性越差。

(2) 地理位置的精确性。移位要改变地图目标的地理位置，从而导致地理位置精度降低。为了保证位置精度，需要根据制图需求、制图规范、地物类型、要素性质等条件，设定地图目标的移位距离阈值R。例如，在较大比例尺地形图上，移位距离一般不超过0.5 mm[28]。一般直接采用地图目标的移位距离衡量其位置精度，移位距离越大，位置精度越低。整幅地图的地理位置精确性评价指标可以用所有建筑物的移位距离总和、最大值、最小值、平均值等统计指标来衡量[24]。

(3) 空间关系一致性。空间关系一致性主要指移位前后拓扑关系、方向关系和邻近关系等需要保持相似性。相关约束定量化评价计算量较大，且标准难以统一，很难通过定量化的目标函数来衡量。因此，需要构建地图辅助数据模型(例如，三角网、邻近图和Voronoi图等)来帮助人们识别、表达和保持这些复杂的空间关系特征。本文通过构建基于Voronoi图和缓冲区的移位安全区限制建筑物的移位范围，以期尽量保持移位前后空间关系的一致性，详见1.3节。

(4) 空间分布特征一致性。空间分布特征一致性主要指地图目标群的空间分布模式的保持，包括建筑物群的局部排列模式和总体分布特征等。相关的约束指标的计算量很大，也难以在目标函数中表达，需要采用相关策略加以约束。对于建筑物群的局部模式需要移位前先识别之，然后移位过程中通过一定的策略加以维护[23,29]。本文借鉴文献[23]中的策略，将地图中呈阵列式、直线式、弧线式等模式分布的建筑物群作为整体移位(图1)。移位时，将建筑物子群合并，用合并后的整体图形参与冲突检测和移位，移位结束后再分解。但对于建筑物分布密度这种总体空间分布特征，依然借助1.3节中构建的移位安全区加以控制。

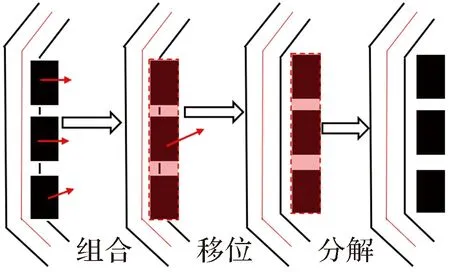
图1 呈直线排列建筑物群的整体移位示意Fig.1 Schematic diagram of overall displacement of buildings arranged in a straight line

1.2 目标函数定义

将地图定义为由若干分区构成的一个集合M={P1,P2,…,Pm}，其中m是分区数。每个分区是一个二元组Pi(L,O)，其中i∈{1,2,…,m}，L={l1,l2,…,lp}为道路集合，B={b1,b2,…,bq}为建筑物集合,p和q分别是分区Pi中道路和建筑物的个数。每个分区内可能存在两种冲突：建筑物与建筑物之间冲突(BB型冲突)、建筑物与道路之间冲突(BL型冲突)。参考文献[27]，两类冲突大小的评价函数分别定义为

fBB(bi,bj,BBmin)=max[0,(BBmin-BBDij)]

(1)

fBL(bi,lj,BLmin)=max[0,(BLmin-BLDij)]

(2)

式中，BBmin是两个建筑物之间的最小距离阈值；BBDij是建筑物bi与bj之间的最小距离；BLmin是建筑物与道路之间的最小距离阈值；BLDij是建筑物bi与道路lj之间的最小距离，i∈{1,2,…,q}，j∈{1,2,…,p}。

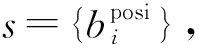
g(s)=w1×f1+w2×f2+w3×f3

(3)

(4)

(5)

(6)

式中，f1代表所有BL型冲突的大小之和；f2代表所有BB型冲突大小之和，它们的值用于评价地图清晰性，单个冲突大小采用式(1)、式(2)计算；f3代表所有建筑物移位距离总和，用于评价位置精度，其中dxi和dyi分别表示建筑物bi在X和Y方向的移位值；w1、w2和w3分别表示以上3项的权重。显然，g值越小，对应的地图状态越好。

1.3 移位安全区的建立

以上目标函数中并没有体现与空间关系和空间分布特征相关的约束指标，需要补充相关附加条件。Voronoi图被广泛用于地图中建筑物群的空间关系、空间结构和空间分布的识别与描述[23,30]。因此，本文采用Voronoi图进一步约束建筑物群的移位范围。将每个建筑物的半径为R的缓冲区多边形和其Voronoi多边形叠加求交，构建移位安全区(图2)。这种移位安全区既可保证每个建筑物的位置精度，也能较好地保持整个建筑物群的相对空间关系和总体空间分布特征，防止产生拓扑错误。

图2 移位安全区构建方法Fig.2 The method of constructing displacement safety zones

综上，一个地图分区中建筑物群的移位问题可以定义为在移位安全区限制下，求目标函数g最小值的最优化问题，其数学模型为

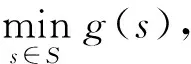
(7)

式中，g(s)为目标函数，由式(3)给出；posi为地图分区中第i个建筑物bi在当前状态s中的位置；Ωi为建筑物bi的移位安全区，其中i∈{1,2,…,q}。

2 基于免疫遗传算法的建筑物群移位算法设计

2.1 免疫遗传算法总体流程

免疫遗传算法将基本遗传算法和免疫理论相结合，有效改善了传统遗传算法早熟收敛的缺陷，提高了算法的局部和全局搜索能力[31]。文献[18]将免疫遗传算法用于解决建筑物群的移位问题，将移位候选解编码成抗体基因，每个抗体表示地图分区在移位过程中的某个状态，N个抗体构成一个种群，通过亲和力函数评价单个抗体的质量，采用免疫遗传操作(包括精英保持策略、选择、交叉和变异等)对种群逐步优化，直至达到算法收敛条件，最后以末代种群中最优抗体对应的地图状态作为移位结果。本文引入移位安全区的概念对该算法加以改进，并结合算法中抗体编码、种群初始化、亲和力函数、抗体移位空间适宜度和抗体浓度调节等环节做进一步优化，算法的主要流程见图3，具体步骤如下：

图3 算法流程Fig.3 Flow chart of the algorithm

(1) 构建移位安全区，整个算法中抗体初始化、选择、交叉、变异等各个环节均受移位安全区的约束。

(2) 初始化抗体种群。

(3) 对每个抗体进行冲突检测，并计算它们的亲和力。

(4) 根据亲和力挑选最优抗体，判断是否满足收敛条件，即达到设定的阈值或达到最大迭代次数，若满足则算法结束，输出最优抗体，否则进入步骤(5)。

(5) 按照亲和力对种群中的抗体进行排序，并选出其中的优秀抗体复制到免疫记忆库。

(6) 计算抗体浓度、抗体移位空间适宜度，根据抗体亲和力、抗体浓度、抗体移位空间适宜度计算抗体选择概率。

(7) 执行选择、交叉和变异3项遗传操作，即根据选择概率选择抗体，然后在选中的抗体中根据亲和力大小挑选一部分进行交叉，交叉得到的抗体再以较小的概率进行变异。

(8) 将免疫记忆库中的优秀抗体和经遗传操作得到的新抗体合并构成新一代抗体，然后转入步骤(3)。

2.2 抗体编码和种群初始化

地图中每个建筑物移位时的试探位置所在范围被称为移位向量模板，主要包括离散空间移位向量模板[12-13,16]和连续空间移位向量模板[17]两种。采用连续空间的移位向量模板，理论上可获得更大的搜索空间，因此本文采用后者，并采用实数编码方式表示抗体[18]。对于一个包含n个建筑物的地图分区，以每个建筑物在X和Y方向的移位值进行编码，其抗体编码长度为2n。设u为实数编码对应的一个抗体，表示为u={u1x,u1y,u2x,u2y,…,unx,uny}，其中uix，uiy(i=1,2,…,n)分别为第i个建筑物X方向和Y方向的移位值。

编码时，对于每个建筑物，还需要考虑移位安全区的限制，将位于移位安全区之外的候选位置剔除。首先，对每个建筑物，生成一定数量的[-R，R]之间的随机数对，作为其X和Y方向的初始移位量。按照初始移位量移位后，建筑物不一定保持在移位安全区之内，需要做进一步筛选，将移位距离大于R或移位之后建筑物超出Voronoi范围的候选点剔除。如图4所示，以某一建筑物为例说明确定建筑物候选点的过程。图4(a)中虚线包围区域为该建筑物对应的Voronoi区域，圆形区域为以该建筑物中心为圆心，以R为半径的缓冲区，其中包含了所有落在精度范围内的候选点。图4(b)放大显示了初始候选点；图4(c)中为最终满足移位安全区约束的候选点。为每个建筑物确定了满足条件且足够数量的候选点后，即可在此基础上按照种群规模产生抗体的初始种群。在后续种群进化过程中，新产生的抗体中每个建筑物对应的位置也需要符合以上条件。

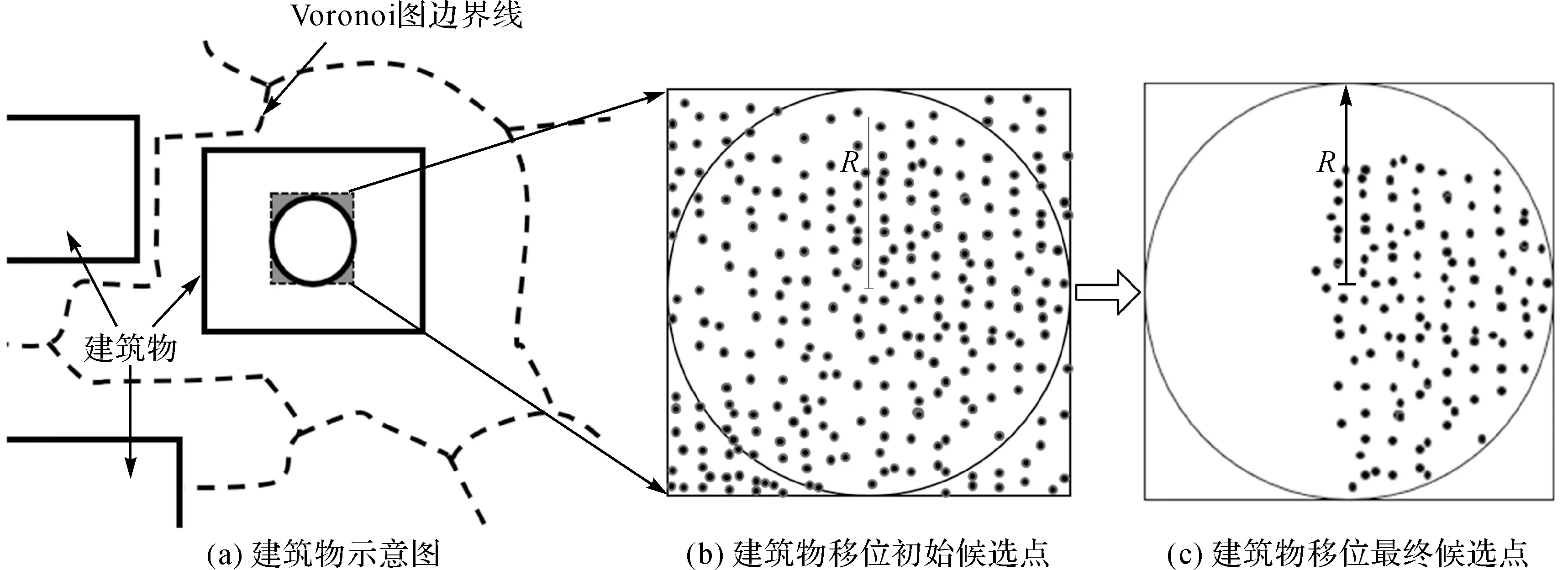
图4 确定建筑物移位候选点的过程Fig.4 The process of determining the candidate points of building displacement

2.3 抗体亲和力函数

亲和力函数由目标函数变换而来。在免疫遗传算法中，亲和力越大，对抗体的评价越好。因此，亲和力函数定义为

Fit(g)=1/(1+g)

(8)

式中，Fit(g)是关于目标函数g的亲和力函数，目标函数定义见1.2节。g的值越小，Fit(g)的值越大，建筑物群移位的效果越好。目标函数g是恒大于0的，因此亲和力函数Fit(g)不会出现小于或等于0的情况，可保证算法正常运行。由抗体亲和力确定的抗体选择概率为

(9)

式中，Fiti为第i个抗体的亲和力值；N为种群大小。

2.4 抗体移位空间适宜度调节

移位安全区不仅限定了每个建筑物的移位范围，其面积也可作为对应建筑物附近区域开阔程度的量化指标。移位操作中，笔者更希望处于开阔区域的目标优先移动，为其他冲突的建筑物释放更多的移位空间。因此提出抗体移位空间适宜度的概念及其量化指标，对那些在开阔区域具有较大移位量的抗体赋予更大的选择概率，从而在选择抗体时引入地图空间格局相关干预，吸引移位向开阔区域传播。抗体移位空间适宜度的计算公式定义如下

(10)

式中，SFiti为第i个抗体的移位空间适宜度；ri为第i个抗体中每个建筑物的移位距离平方值与可移位面积的相关系数，可通过式(11)计算，rmin与rmax是整个种群中相关系数的最小值与最大值。

(11)

式中，Di为第i个抗体所表示的移位方案中，所有建筑物的移位距离的平方构成的向量；Ai为所有建筑物的安全区面积构成的向量；Var[Di]为Di的方差；Var[Ai]为Ai的方差；Cov(Di,Ai)为两者的协方差。对应的抗体移位空间适宜度选择概率计算公式为

(12)

2.5 抗体浓度调节

算法中抗体的选择概率还采用了抗体浓度进行调节。在传统的遗传算法中，如果相似的和非最优的抗体占了太大的比例，就需要降低它们的选择概率，否则就很容易过早收敛。在选择时通过适当抑制高浓度抗体，可以有效提升种群的多样性，从而防止早收敛。抗体浓度的计算公式为

(13)

式中，N为种群大小；Ni为与第i个抗体相似的抗体数量；Ci为第i个抗体对应的浓度。对应的第i个抗体的抗体浓度选择概率的为

(14)

最后，由抗体亲和力、抗体移位空间适宜度和抗体浓度共同确定的抗体的选择概率为

Pi=αPfi+βPsi+γPdi(i=1,2,…,N)

(15)

式中，α、β和γ为3种选择概率的权重，且满足α+β+γ=1。

3 试验与讨论

3.1 数据准备和算法参数设置

采用C#编程语言实现免疫遗传算法、冲突检测和Voronoi图生成等算法。基于CDT三角网提供的邻近关系，对每个建筑物周围的对象进行距离量测，若距离小于设定的阈值，则判定为冲突，并计算冲突大小[18]。进行移位之前先进行初始冲突探测，若不存在冲突，则算法结束，若存在冲突，则调用免疫遗传算法进行移位。

试验数据选择北京市中心城区部分街区的建筑物群(图5)。地图目标比例尺为1∶10 000，街道符号宽1.2 mm，建筑物轮廓线宽0.1 mm，因此地图上街道与建筑物之间最小距离阈值为0.85 mm(BLmin=0.85 mm)，建筑物之间最小距离阈值为0.3 mm(BBmin=0.5 mm)，最大移位距离设为0.5 mm(R=0.5 mm)。目标比例尺下，由于符号拥挤产生了建筑物与街道、建筑物与建筑物的邻近冲突。首先采用分治策略，以街道为边界将地图分为8个区，然后分别对每个分区调用算法解决冲突。

移位时，为了保持建筑物的局部模式，位于相同模式中的建筑物被作为一个整体处理[23]，即将同一模式的多个建筑物合成一个目标，用合并后的整体图形参与冲突检测和移位，完成移位后再分解。因此，首先需识别各分区内建筑物的典型模式，包括线性模式、阵列模式等。关于建筑物群的模式识别超出了本文的研究范围，这里主要借鉴文献[29]提出的识别方法。其主要思路是在构建建筑物群邻近图的基础上，依据格式塔完形原则，将具有相似的形状、尺寸和方位等特征的多个建筑物划分为模式子群。其中线性模式是最基本的模式，多个相互交错的线性模式又可以组成更复杂的阵列模式。采用该方法从试验数据识别出的模式及其合并图形，在图5中以红色半透明多边形标绘。在分区3、7、8中识别出7组建筑物线性排列。其中分区3中存在一个特大的网格状建筑物群，可看作一个由4行7列线性模式复合而成的阵列模式，本可作为一个整理处理，但由于此网格模式内部各列之间存在冲突(各行间无冲突)，为了解决这些冲突，将其拆分为4组纵向的线性排列分别参与移位。

结合前人经验[17-18]，试验中将免疫遗传算法的种群大小设为分区中初始冲突数的4倍，最大迭代次数设为分区中建筑物个数的15倍，目标函数中各项权值分别为w1=100、w2=50和w3=1,交叉率、变异率分别为0.75和0.1，抗体相似度阈值为0.8，计算选择概率时3种选择概率的权重分别为0.5，0.25和0.25(α=0.5,β=0.25,γ=0.25)，免疫记忆库中的优秀抗体占种群大小的10%。

3.2 初步试验

调用算法对图5中的建筑物移位，得到结果如图6所示。表1列出了各个分区中建筑物的个数、初始冲突大小、初始冲突个数、剩余冲突大小和剩余冲突个数。总体上，初步移位后剩余冲突大小和个数仍较多，主要集中在分区3、7和8中，剩余冲突大小分别为5.14 mm,1.4 mm和2.75 mm。其他分区的剩余冲突较小，其中最大为分区6中的0.43 mm。

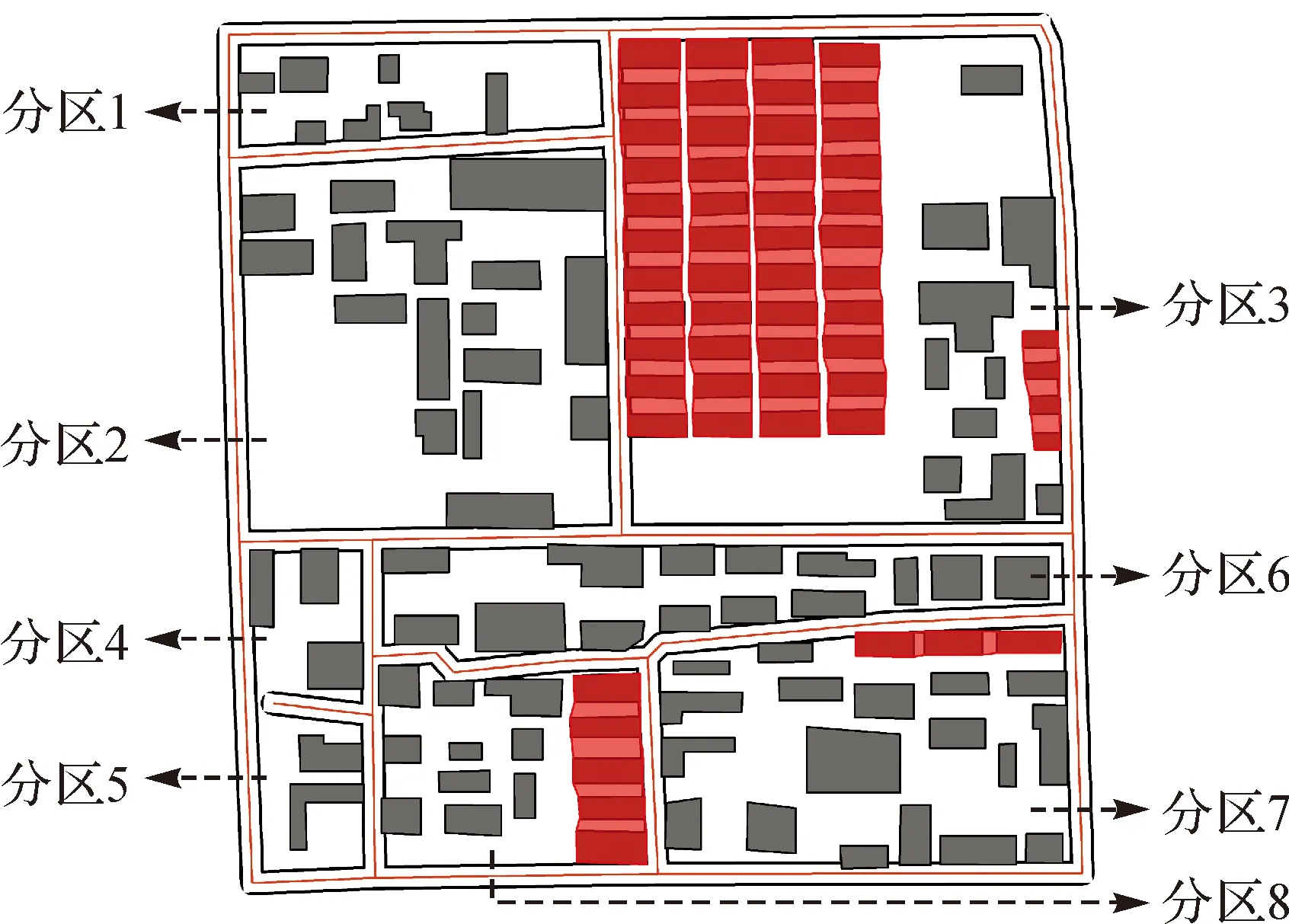
图5 移位前地图及其分区(1∶10 000放大至1∶5000)Fig.5 The map and its segments before displacement (enlarged from 1∶10 000 to 1∶5000)

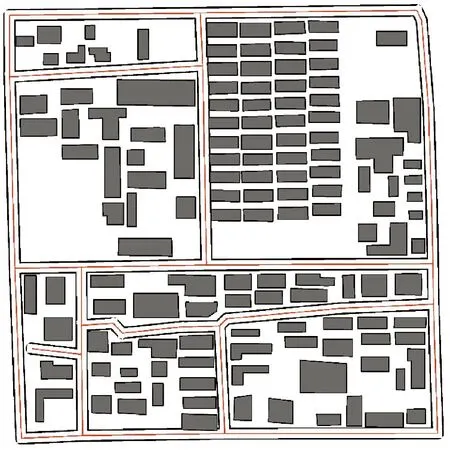
图6 初步移位结果图(1∶10 000放大至1∶5000显示)Fig.6 The result of preliminary displacement (enlarged from 1∶10 000 to 1∶5000)

表1显示移位后冲突个数没有冲突大小减少得明显，BB冲突没有BL冲突减少得多，这与本文所采用的目标函数及其相关权值有关。目标函数中将冲突大小作为地图清晰性评价指标，而非冲突个数。冲突大小是一种连续变量，与移位距离的单位一致，这可保持目标函数中各项指标量纲达到统一，并且采用这种连续变量作为地图清晰性评价指标可提高评价结果与视觉感受的一致性。例如分区2中剩余冲突个数虽高达4个，但对应的冲突大小仅为0.2 mm，显然冲突大小更符合视觉感受。目标函数中，BL冲突比BB冲突具有更大的权值，可促进BL冲突优先被解决，甚至会为了解决BL冲突而引起新的BB冲突，这种策略是符合实际的移位操作逻辑的，因为建筑物群的移位往往是由于街道符号扩宽而触发，在移位过程中逐步传播到远离道路的建筑物[3,23]。

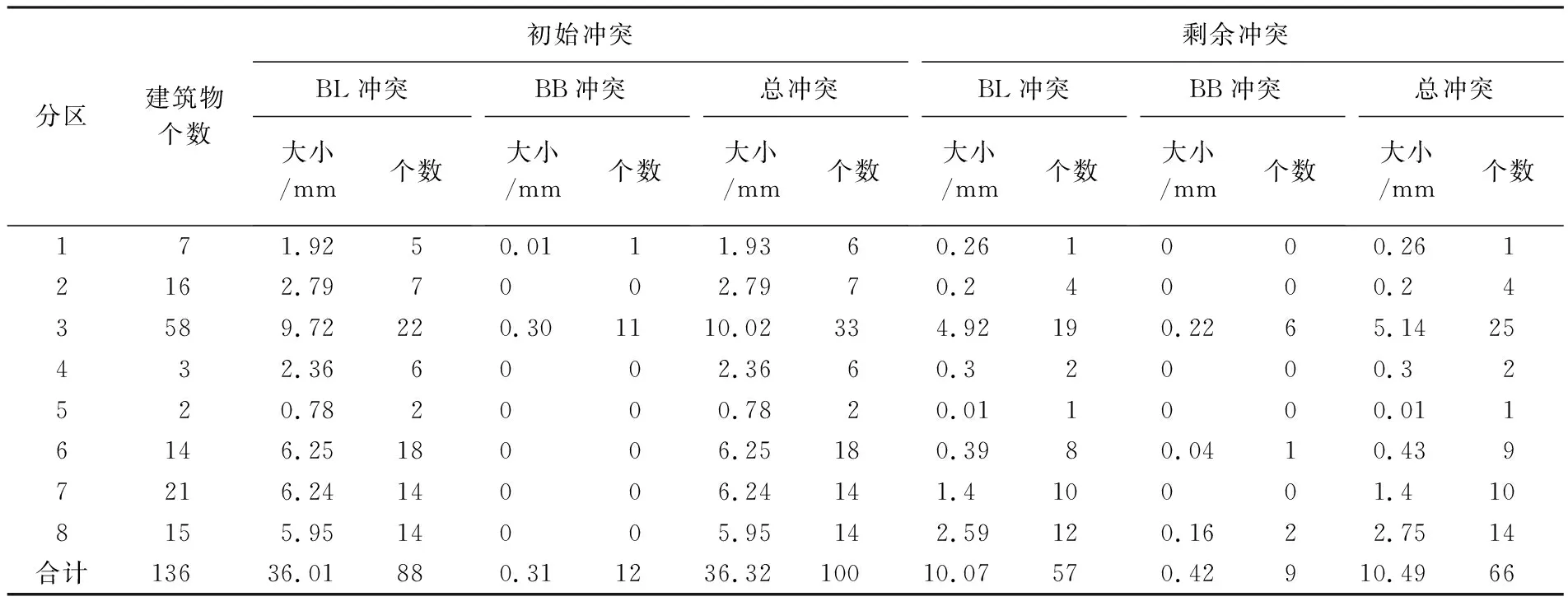
表1 各个分区移位前后冲突对比

3.3 分阶段渐进式优化试验

初步试验结果中存在不少剩余冲突。尤其在分区3、7和8中，由于建筑物较多，且在多处形成局部聚集模式，导致其中的移位安全区非常狭小，冲突的建筑物无法通过足够的移位解决冲突。图7以分区3为例标记了存在剩余冲突的建筑物(或群组)，这些建筑物(或群组)已经移动到安全区的边界，已没有进一步移位的可能。其他分区中也存在类似情况。可见，本文提出的移位安全区对于建筑物比较拥挤区域的限制太严苛，需要适当放宽条件。

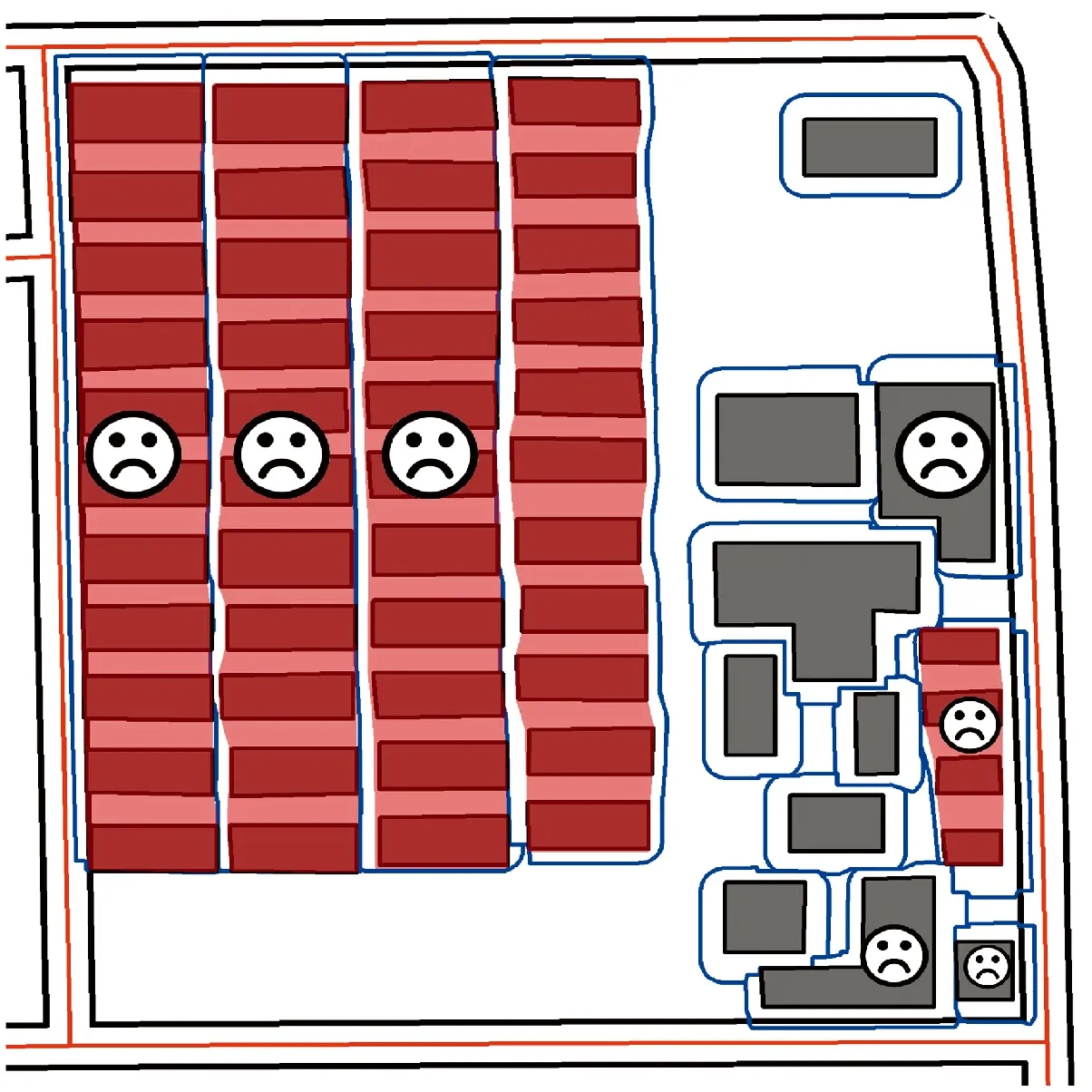
图7 分区3的初步移位结果及其移位安全区Fig.7 The preliminary displacement result of segment-3 and its displacement safety zones

为了放宽移位安全区的限制，试验中采用了多阶段渐进式移位策略，即分阶段调用算法若干次，每次调用时，将上一次的移位结果作为输入，这样移位安全区也会在上一阶段的基础上重新生成，从而逐渐地放松移位范围的限制。经试探，分2～3个阶段移位可得到较好的结果。因此在优化试验中对每个分区分别进行2次移位，每次的最大移位距离设为R/2(R=0.5 mm),经2次调用算法后，移位效果明显改善(图8)。在优化试验中，第1阶段移位后，总冲突大小从36.32 mm减少到21.53 mm，再经过第2阶段处理，总冲突大小最终减少到4.61 mm，这比初步试验中的10.49 mm降低了不少(表2)。分区1、2、4和5中的冲突大小和冲突个数几乎全降到了0。然而，在比较拥挤的分区3、6、7和8中，冲突大小尽管也有明显减小，但最终无法解决所有冲突。说明当地图上符号密度不大，存在足够移位空间的时，通过本文算法是能解决所有冲突的；但当地图上符号比较密集，没有足够的空间移位时，剩余的冲突无法仅通过移位解决，还需要配合采用典型化、删除、合并等降低图幅密度的地图综合操作。篇幅所限，此处不对移位之外的综合算子做进一步讨论。

图8 两阶段渐进式移位结果(1∶10 000放大至1∶5000显示)Fig.8 The result of 2-stage progressive displacement (enlarged from 1∶10 000 to 1∶5000)

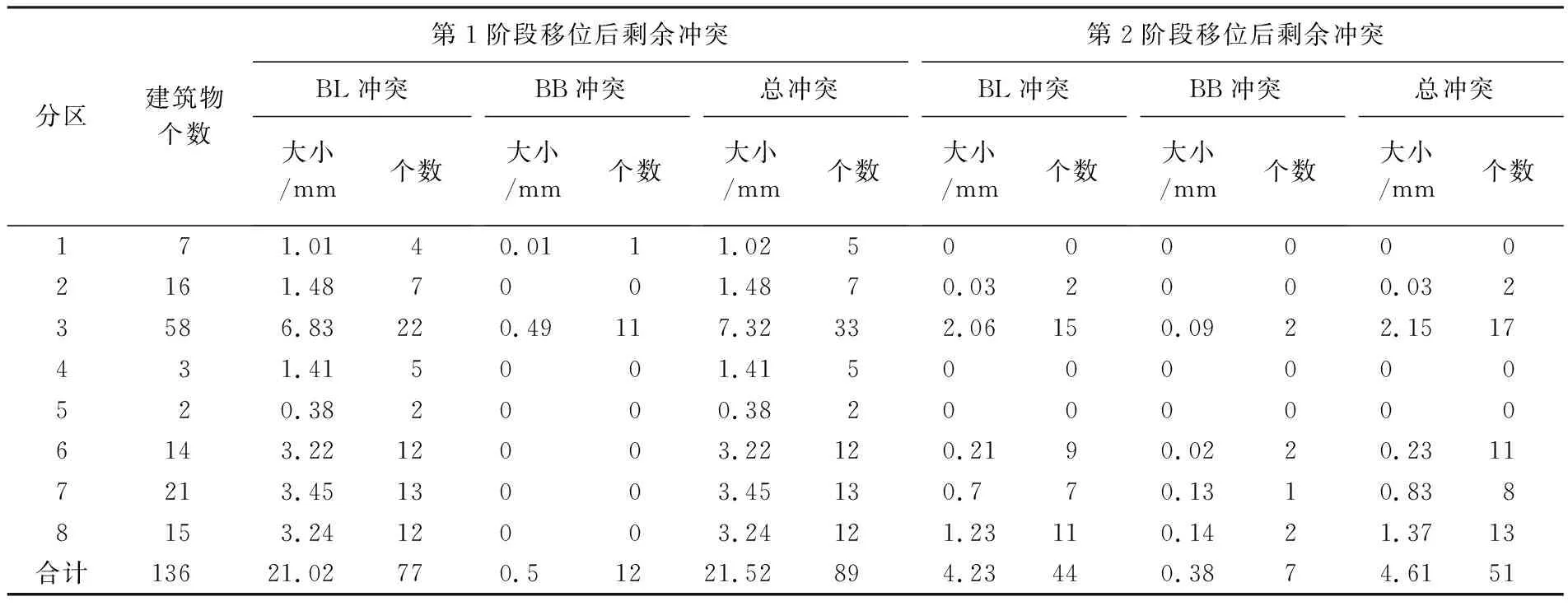
表2 对各分区分别采用2阶段渐进式移位的剩余冲突变化情况

为了定量评价移位前后建筑物群的空间分布变化情况，借助Voronoi图计算移位前后每个建筑物的空间分布密度，其公式为

(16)

式中，ai是第i个建筑物的面积；Ai是其对应Voronoi多边形的面积。图9(a)是移位前后建筑物及其Voronoi图的对比效果。在图9(b)中横、纵坐标分别为移位前、后各建筑物的分布密度，通过直线拟合得到横纵坐标的关系为：y=0.899 8x+0.05，其确定系数(R2)为0.928 3，说明移位前后建筑物的分布密度高度相关；另外通过统计计算得到每个建筑物移位前后分布密度比值的平均值为0.979、标准差为0.078，说明位移前后建筑物分布密度比值集中分布于0.979附近(图9(c))，从定量角度说明本算法良好地保持了建筑物群相对位置关系和空间分布特征。

图9 移位前后建筑物的分布密度对比Fig.9 Comparison of distribution densities before and after displacement

3.4 对比试验

为了进一步证明本文相对于以往算法的改进是有效的，笔者模拟了文献[18]的算法，并将试验结果与3.3节中的优化试验结果作对比。文献[18]中采用半径为R的矩形区域作为建筑物的移位范围，采用冲突个数作为地图清晰性评价指标。因此，该算法中目标函数(式(3))的前两项f1和f2分别是BL冲突个数和BB冲突个数，f3仍然是总移位距离，对应的权值w1、w2和w3分别设置为100、50和10。为了具有可比性，其他参数与3.1节中的设置保持一致。对比试验结果如图10所示，从视觉效果看，结果并不理想，在建筑物分布比较稠密的分区3中甚至出现了多处拓扑错误，即建筑物与建筑物、建筑物与街道中心线的重叠。

表3列举了本文算法和文献[18]算法的剩余冲突对比情况。文献[18]算法剩余冲突大小为17.65 mm远大于本文算法的4.61 mm，说明本文算法更优。而文献[18]算法的剩余冲突个数却仅为31个，比本文算法的51个少很多，这与图8和图10中的视觉感受并不一致。与之前的试验结果类似，剩余冲突基本集中在分区3、6、7和8中，尤其是分区3中甚至产生了7个严重的拓扑错误。证明本文提出的移位安全区对于保持建筑物群的空间关系和分布特征、防止移位中产生严重的拓扑错误是有十分有效的。当地图上建筑物比较密集，且没有移位安全区的限制时，算法可能会为了减少冲突个数而容忍非常严重邻近冲突或拓扑错误产生。因为这种冲突可以为周围的地图目标腾出更多的空白区域，从而有效减少冲突个数，而这种情况在实际地图综合过程中是不可接受的。这也说明从提高算法稳定性角度考虑，采用“冲突大小”代替“冲突个数”作为地图清晰性评价指标更合理。

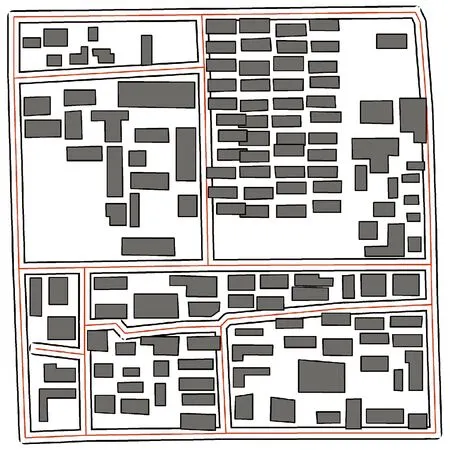
图10 文献[18]算法移位结果图(1∶10 000放大至1∶5000)Fig.10 The result of the algorithm in reference [18] (enlarged from 1∶10 000 to 1∶5000)

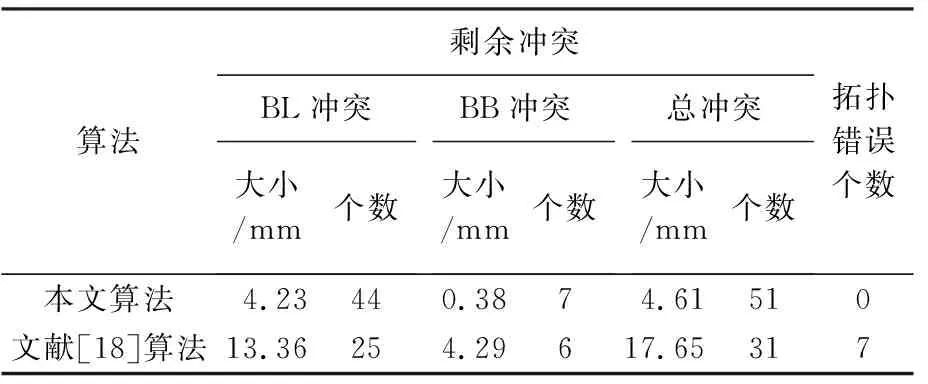
表3 本文算法与文献[18]算法剩余冲突对比

表4分别给出了两组试验的移位量统计值。可以看出，本文算法的移位距离被严格控制在距离阈值0.5 mm之内，说明采用移位安全区对保证建筑物的位置精度是可靠的。两者的总移位量分别为50.32 mm和39.87 mm，虽然本文算法的总移位量略大，但这些移位对于解决冲突更有效。为说明其有效性，此处提出移位效率的概念，用于定量评价移位总距离对解决冲突的有效程度，其计算公式为

表4 本文算法与文献[18]算法移位距离对比

(17)

式中，τ为移位效率；initalCtotal和remainderCtotal分别为初始总冲突大小和剩余总冲突大小；displacementtotal表示总的移位量。经计算，本文算法移位效率为63.0%，而文献[18]算法移位效率仅为46.8%。

4 结 论

将免疫遗传算法用于建筑物群移位问题，对相关约束指标进行定量化评价，建立通用的目标函数，再借助智能优化算法从全局角度解决冲突，降低了移位算法的设计难度，但仍需要在算法中引入更多与制图综合相关的补充条件和后继策略。针对移位过程中地图目标群的空间关系和空间分布特征一致性保持问题，本文提出移位安全区约束下的建筑物群移位免疫遗传算法，将建筑物群的缓冲区和Voronoi图叠加，构建每个建筑物的移位安全区，可有效保持移位前后的空间关系和全局空间分布特征的一致性，避免了严重拓扑错误的产生；同时，采用建筑物模式整体移位策略，可有效保持建筑物群的局部模式。

在算法的目标函数中，采用冲突大小(连续变量)作为地图清晰性的评价指标，比冲突个数(离散变量)更符合人类视觉感受。对于高密度区域，构建的移位安全区过于狭窄，导致较多剩余冲突无法解决，实际应用中可采用分阶段渐进式移位策略，适当放松移位安全区的限制，从而更充分地解决冲突。

本文所采用的免疫遗传算法比较耗时，且相关参数的设置对移位效果和算法的收敛性有一定影响，其选择缺少普适方法，还需依靠经验。下一步将针对算法效率的提高、算法参数设置等问题进行更深入的研究。试验结果也表明，仅仅采用移位并不能解决所有冲突，还需将移位操作与其他地图综合算子结合，协同处理各类冲突。