考虑多特征的高速公路交通流预测模型

李桃迎，王婷，张羽琪

(大连海事大学，航运经济与管理学院，辽宁大连116026)

0 引言

高速公路交通拥堵现象不仅给人们出行带来极大不便，也制约了高速公路服务质量的提升，影响区域经济和社会发展。虽然高德地图、百度地图等多款APP都提供了实时交通状态查询，但并未提供未来12 h、24 h 甚至更长时间的交通流预测功能。提前一天或多天预知高速公路交通流，不仅可以辅助高速公路管理人员提前安排部署、合理诱导车辆分流、疏散，缓解高速公路拥堵现象，也可以为公众出行提供参考。

高速公路交通流预测作为研究热点在不同发展时期均取得较为丰硕的成果，研究趋势从单一的参数模型过渡到非参数模型及混合模型。典型的参数模型有自回归积分移动平均(Autoregressive Integrated Moving Average，ARIMA)模型和卡尔曼滤波器模型。如Williams 等[1]提出使用季节性ARIMA 模型对交通流进行预测以提高预测精度。相较于非参数模型，参数模型依赖于平稳性假设，不能反应交通流的非线性和不确定性特征，因此，非参数模型成为交通流预测的有效方法。非参数模型包括支持向量机回归(Support Vector Regression,SVR)模型、贝叶斯模型以及深度学习模型[2]等。其中，深度学习模型通过其强大的非线性拟合和深层特征表达能力可以更精准地表达交通流数据内部的复杂结构。如Zhao 等[3]将长短期记忆(Long-Short Term Memory,LSTM)神经网络应用于交通流预测以提高模型预测精度。Wu 等[4]提出将卷积神经网络(Convolutional Neural Network，CNN)和门控循环单元神经网络(Gated Recurrent Unit，GRU)结合，CNN捕获路网交通数据的空间分布，GRU捕获数据短期分布的变化及长期依赖。

LSTM 能够处理具有长期依赖关系的时序数据，而GRU是LSTM的变体，通过牺牲预测精度而减少计算量。LSTM和GRU的集成解决了多层LSTM计算量大的问题，同时又维持了模型的精确度。但LSTM和GRU只能提取交通流的动态时序特征，无法提取交通流数据的空间相关性，往往需要手工将空间信息编码作为网络输入。为了更好地刻画交通流的空间特征，一些学者又引入了CNN 进行空间建模，通过CNN 共享卷积核能够处理高维数据，并自动学习数据的空间特征，从而提高模型的预测精确度，但单一CNN 模型只能捕捉短期局部依赖关系。

由于高速公路交通流的变化不仅与历史交通流存在长期的时间依赖关系，还与其上下游交通流的空间分布存在明显相关性，且容易受天气、路况等外界环境影响，为此，本文针对高速公路交通流的时空特性和外部因素影响，提出考虑多特征的高速公路交通流预测模型。该模型利用CNN自动提取交通流的空间特征，运用LSTM和GRU 提取数据的周期性和趋势性特征，解决时序数据的长期依赖性问题。采用某高速公路交通流数据进行实验，验证本文模型的预测精度。结果表明，本文模型与4 种典型深度学习模型(LSTM、GRU、CNN-LSTM、CNN-GRU)相比具有更高的预测精度。

1 集成深度学习预测模型

本文所提模型为一种集成深度学习模型(Hybrid Deep Learning，HDL)，其框架如图1所示，主要包括数据预处理、特征矩阵构建、CNN和LSTM、GRU 这4 个方面。该模型首先针对高速公路交通流数据进行预处理，构造包含时空和天气的二维特征矩阵，随后将构造的二维特征矩阵经过CNN提取交通流的空间特征，然后利用一层LSTM和一层GRU 提取交通流的时间特征，最后通过全连接层，得到最终输出的结果。

图1 集成深度学习模型的框架Fig.1 Framework of Hybrid deep learning model

1.1 数据预处理与滑动窗口

高速公路交通流数据和天气数据存在数据缺失的问题，为提高数据质量需要考虑数据的预处理。线性插值是代数插值法中最简单的形式，是处理非线性函数运用最多的方法，其以线性平滑的方式维系了数据趋势的渐进性，适用于连续缺失长度小的数据集。鉴于此，本文选择线性插值作为缺失值填充的方法。

其次，为保证预测结果的可靠性，对数据进行分析之前，先将数据进行归一化处理，消除不同属性之间的量纲。选用应用最为广泛的min-max 方法对原始数据进行线性变换，将数据统一映射到[0,1]区间上。min-max方法的公式为

式中：xi为第i个原始数据；为归一化后的新数据；xmin为最小值；xmax为最大值。

随后，考虑到外界因素对交通流预测结果的影响，将数据中的属性两两之间进行皮尔逊相关性分析，并根据相关系数大小选取相关特征。

另外，时间序列数据的序列长度可能影响预测精度，本文采用滑动窗口方法[5]确定序列长度，该方法为每一个时间序列t构造一个样本。[t0-Δt,t0)上的值作为特征，t0作为标签构造样本，Δt被称为窗口大小。为了更直观地介绍滑动窗口方法，图2给出利用滑动窗口构造时间样本序列的例子。该例假设有10 条时间序列记录，包括T1,T2,…,T9、T10。当Δt=5 时，对于样本1来说，T1,T2,…,T5作为特征，T6作为标签；对于样本2 来说，T2,T3,…,T6作为特征，T7作为标签。以此类推，共得到5个样本；当Δt=6 时，T1,T2,…,T6作为特征，T7作为标签，以此类推，共得到4个样本。

图2 滑动窗口Fig.2 Sliding window

窗口大小会影响构造样本的数量和样本中的特征数量。可以看到：当给定一个数据集，窗口越小，单个时间序列涵盖的时间越短，构造的时间序列样本越多；窗口越大，单个时间序列涵盖的时间越长，构造的时间序列样本越少。因此，选择一个合适的窗口大小对高速公路交通流预测至关重要。

1.2 构建特征矩阵

由于当前道路交通流的变化与该道路的历史交通流，上下游的交通流以及天气的变化相关。构建一个包含时间、空间以及天气信息的二维特征矩阵，即

式中：t时刻的交通流量数据为{xs1,t,xs2,t,…,xsm,t}，其中，xsm,t为第m个目标站口sm在t时刻的交通流量数据；t时刻的天气数据为{wq1,t,wq2,t,…,wqn,t}，其中，wqn,t为第n个天气属性qn在t时刻的数据量；Δt为窗口大小；xsm,t-Δt为站口sm在当前时间前Δt个时间统计单位的时刻交通流量数据；wq1,t-Δt为天气属性q1在当前时间前Δt个时间统计单位的时刻数据。

1.3 卷积神经网络

CNN 是一个多层监督学习网络，用来处理类似网格结构的数据，被广泛应用于图像分类、语音识别、自然语言处理等领域，并获得显著成果。在处理时间序列型数据时，一维CNN 可以很好地识别出数据的简单空间模式，并据此在更高级的层中生成更复杂的模式。CNN 主要由卷积层、池化层和全连接层构成，3个级联层描述为

式中：xl-1,i为卷积层的输入；cl,j为卷积层的输出，同时也是激活层的输入；xl,j为激活层的输出；wl,ij为第l层第j个单元和上一层第i个单元之间的权重；b为偏置项；φ(⋅)为非线性的激活函数；pool(⋅)为池化函数。式(3)表示CNN网络中的卷积运算。

高速公路交通流数据具有周期性、长时间变化的特性，在构建特征矩阵之后，将特征矩阵输入到一维的CNN中，以提取交通流数据的空间特征。

假设将一个样本为504×7的矩阵输入一维卷积，经过64 个大小为2的滤波器后，输出的特征维度为503×64，如图3所示。

图3 数据经过一维卷积后的结果Fig.3 Results of data after 1-D convolution

1.4 长短期记忆网络和门控神经网络

运用CNN 提取数据空间特征后，需要提取高速公路交通流数据的时间特征。LSTM 是RNN的结构变种，是解决长期依赖问题的有效技术。与传统RNN的区别在于它在算法中加入了一个判断信息有用与否的“处理器”，该处理器作用的结构被称为cell，具体涉及3 个门函数：输入门、遗忘门和输出门，分别控制输入值、记忆值和输出值。当一个信息输入LSTM网络时，网络根据规则判断该信息是否有用。只有符合算法认证的信息才会留下，无用的信息则通过遗忘门被遗忘。

而GRU 相较LSTM 结构更简单，收敛速度更快。GRU同样可以解决RNN网络中的长期依赖问题，也是当前非常流行的一种网络。GRU 中引入两个门函数，如图4所示。

图4 GRU结构图Fig.4 Structure of GRU

式中：σ(⋅)为sigmiod激活函数；Xt为当前t时刻的输入；Ht-1为上一时刻即t-1时刻的输入；Wxr、Wxz和Whr、Whz分别为当前时刻和上一时刻的权重参数；br、bz、bn为偏置项；为候选的隐含状态；Ht为最终的隐含状态；⊙为哈达玛积。重置门Rt有助于捕捉时序数据中短期的依赖关系，更新门Zt有助于捕捉时序数据中的长期依赖关系。且式(8)满足

式(9)满足

在CNN 提取空间特征之后，经过扁平层和防止模型过拟合的Dropout 层，再经过一层LSTM和一层GRU，提取交通流数据的时间特征，最后通过一层全连接层，得到预测结果。

2 高速公路交通流预测

2.1 数据来源与趋势分析

本文所用数据集来自KDD CUP 2017 提供的某省某高速公路交通流数据和天气数据。目标区域路网拓扑如图5所示。交通流数据来源于3个收费站(1、2、3号，除了2号收费站只允许车辆进入高速公路，其他收费站允许车辆双向通行(入口：0，出口：1))，交通流数据的时间周期为2016年9月19日-10月17日，数据频率为每隔20 min记录一条，即1 d有72条数据记录。收费站1号，入口(1-0)共有2084条记录，出口(1-1)共有2084 条记录；收费站2 号入口(2-0)共有1725 条记录；收费站3 号，入口(3-0)共有2086 条记录，出口(3-1)共有2085 条记录。在该期间，收费站1 号入口、出口的交通流量数据各有缺失值4 个，收费站2 号入口的交通流量数据共有缺失值362个，收费站3号入口、出口的交通流量数据各有缺失值2 个、4 个。天气数据的时间周期为2016年9月19日-10月17日，天气数据包含气压、海水压力、风向、风速、温度、湿度、降雨量共7个特征，数据频率为每隔3 h记录一条，而一天中天气指标数据的值通常是连续变化的，故将天气数据通过频率线性填充为每隔20 min 一条记录。以降雨量数据为例说明天气数据的可靠性，图6为降雨量与交通流量数据的关系，可以看出，当降雨量累计超过15 mm时交通流才会有明显变化，而累积降雨量随着时间的推移呈连续上升趋势，通过线性插值方法可以较好地拟合降雨量的累积过程[6]，如图7所示，将频率间隔为3 h的降雨量平均分割成9段，即每隔20 min一个值，最终得到2088个值。

图5 目标区域路网拓扑Fig.5 Road network topology of target area

图6 交通流量与降雨量Fig.6 Traffic flow and rainfall

图7 降雨量的线性填充Fig.7 Linear filling of rainfall

图8给出3个站口各个方向2016年9月19日-10月17日共29 d的交通流变化趋势，可以看到，3个站口交通流变化有很强的相似性，即上、下游收费站的交通流变化具有明显的空间相关性，并且从图中可以看到，高速公路交通流变化有明显的日周期性。图9为气压、海水压力、风速、温度、湿度、降雨量特征取值变化图。

图8 3个收费站口的交通流趋势Fig.8 Traffic flow trend of three stations

图9 特征可视化图Fig.9 Distribution of multiple features

为更好地分析高速公路交通流的时间变化情况，图10分别给出3 周(2016年9月19日-10月9日)、1周(2016年9月21日-9月27日)、1 d(2016年9月20日)的高速公路交通流的变化趋势，可以看出，高速公路交通流具有明显的日周期性、周周期性、趋势性以及复杂性。图10(a)包含国庆期间7 d的交通流数据，可以看出，国庆期间与平日的交通流变化趋势有明显差异。

图10 交通流变化趋势Fig.10 Trend of traffic flow

为评估预测模型的性能，选择平均绝对误差(EMAE)、均方根误差(ERMSE)两个评价指标，即

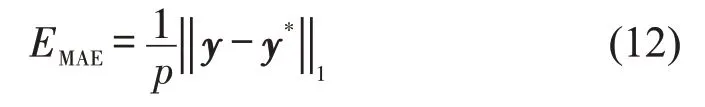
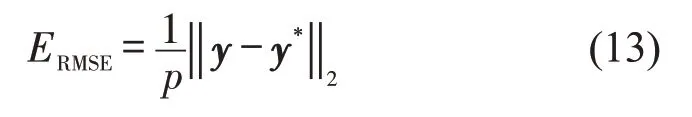
式中：y=(y1,y2,…,yp)为观测值；为预测值；p为交通流数据观测点数量。

2.2 特征选择与滑动窗口设置

对高速公路收费站数据进行缺失值填充和归一化后，分析不同属性和交通流之间的皮尔逊相关系数，以此判定各个属性对交通流变化的影响。一般情况下，相关系数的绝对值越大，相关性越强；反之，相关系数越接近于0，相关性越弱。通常认为：[0.8，1.0]为极强相关，[0.6，0.8)为强相关，[0.4，0.6)为中等程度相关，[0.2，0.4)为弱相关，[0.0，0.2)为极弱相关或无相关。

图11给出站口1-0、2-0、3-0、1-1、3-1的交通流与7 个天气属性之间的皮尔逊相关系数。从图中可以看出，3 个站口双向交通流彼此之间的相关系数绝对值均大于0.6，说明这3个站口双向的交通流之间具有强或极强的相关性，故本文在预测目标站口交通流时，其他站口的交通流均考虑在内。

图11 属性之间的皮尔逊相关系数图Fig.11 Pearson correlation coefficient between attributes

气压与站口1-0、2-0、3-0、1-1、3-1 交通流之间的相关系数分别为：-0.150、0.001、-0.064、-0.013、-0.008，相关系数均小于0.2，说明气压与目标站口交通流的相关性为极弱相关或无相关，故预测目标站口交通流时，不考虑气压对交通流变化的影响。同理，海水压力、风速、风向、温度与站口1-0、2-0、3-0、1-1、3-1 交通流之间的相关系数均小于0.2，说明这些因素与目标站口交通流的相关性为极弱相关或无相关，故预测目标站口交通流时，不考虑这些因素对交通流变化的影响。

湿度与站口1-0、2-0、3-0、1-1、3-1 交通流之间的相关系数分别为-0.260、-0.20、0.210、0.20、0.190，降雨量与站口1-0、2-0、3-0、1-1、3-1交通流之间的相关系数分别为0.270、-0.250、0.210、0.220、0.200，说明湿度、降雨量与目标站口交通流的相关性为弱相关，为确保交通流预测的准确性，预测目标站口交通流时，将湿度、降雨量考虑在内。最终本文同时考虑3 个站点双向的交通流量、湿度、降雨量作为模型输入分别预测1-0、2-0、3-0、1-1、3-1未来1 d的交通流量。

如1.1 节中分析，窗口较小无法保证模型有足够的长期输入，窗口较大则会增加不相关的输入和计算复杂性。因此有必要确定一个最优的窗口大小值，确保模型的预测性能。

2.1节分析得出高速公路交通流数据具有明显日、周的周期性，为了让样本数据保持原本周期性特点，并选择出合适的滑动窗口大小，将滑动窗口值Δt分别设为72(1 d)、144(2 d)、216(3 d)、288(4 d)、360(5 d)、432(6 d)、504(7 d)、576(8 d)进行比较并选择。

表1为不同滑动窗口时，HDL模型预测误差的比较结果。较低的平均绝对误差和均方根误差值表明，该模型预测值与观测值的总离差较小。从表1中可以看出，当Δt=504 时平均绝对误差和均方根误差均为最小，分别为5.530 辆·(20 min)-1、7.700辆·(20 min)-1。所以，将窗口大小设定为504，即将长度为504(7 d)的数据作为输入，预测未来长度为72(1 d)的高速公路收费站交通流。

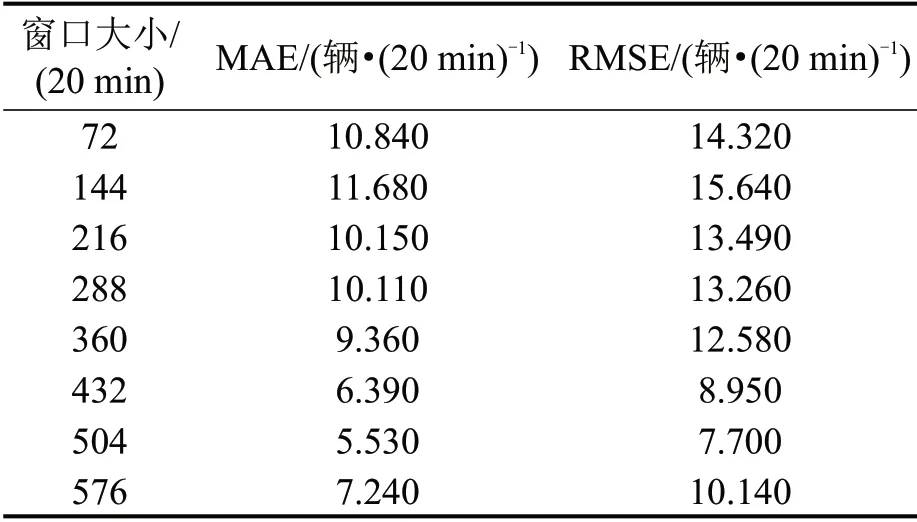
表1 窗口大小对误差的影响Table 1 Influence of window size on error

2.3 网络参数设置

网络结构设置会对预测模型的性能产生很大影响，针对高速公路收费站交通流数据，采用Hyperband 算法[7]对模型中滤波器个数(con_filter，cf)、卷积核数(con_kernel，ck)、池化层(maxpool)、LSTM 单元数(lstm_units，ls)、GRU 单元数(gru_units，gs)、学习率(learning rate，lr)、优化器(optimizer)、Dropout(dp)8 个参数进行优化，确定最佳参数组合。

经过 128 次迭代，得到预测误差(val_loss_score)从小到大的前10组超参数组合，如表2所示，在128次迭代产生的最优值数据中，cf的搜索覆盖范围为2～256，步长为8；ck的搜索覆盖范围为2～8，步长为1；maxpool的搜索覆盖范围为2～8，步长为2；ls的搜索覆盖范围为2～256，步长为8；gs的搜索覆盖范围为2～256，步长为8；lr的值在[0.1，0.01，0.001，0.2，0.02，0.002,…,0.5，0.05，0.005]中选取；optimizer 在[Adam、SGD、RMSprop]中选取；dp的搜索覆盖范围为0.1～1.0，步长为0.1。本文选择误差最小的第1组参数组合。

表2 前10组超参数组合Table 2 Top-10 super parameter set

2.4 结果分析与比较

考虑到工作日和节假日的高速公路交通流变化有明显的差异，分别训练和预测工作日和节假日(国庆假期)的交通流，同时为验证HDL 模型的性能，将其与4种典型的深度学习模型(LSTM、GRU、CNN-LSTM[8]、CNN-GRU[9])进行对比分析，并针对工作日、十一假期做了两组对比实验。其中，工作日交通流预测实验中，考虑到交通流数据的周期性，将2016年9月30日-10月7日交通流数据剔除，3 个站口各个方向均得到936 条训练数据，576条测试数据；十一国庆假日交通流预测实验中，3个站口各个方向均得到864 条训练数据，567 条测试数据。

2.4.1 工作日交通流预测结果

图12为考虑空间、时间、天气特征的HDL模型和4种典型深度学习模型对3个收费站口各个方向(1-0、2-0、3-0、1-1、3-1)的交通流预测结果(以2016年10月12日为例)。从图12中可以看出，本文所提HDL模型的预测值与期望值吻合度均为最高。

图12 5种模型对3个站口各个方向交通流预测结果Fig.12 Prediction results of traffic flow in all directions of three stations by five models

表3为HDL模型对3个站口各个方向在8 d工作日(2016年10月10日-17日)的交通流预测误差。

表3 HDL模型对8 d工作日的预测误差Table 3 Prediction error of HDL model for eight working days

为评估模型稳定性，表4给出5种模型对8 d工作日(2016年10月10日-17日)的平均预测误差。

由表4可知，预测工作日交通流时，本文所提HDL模型的MAE和RMSE在3个站口各个方向上的平均预测误差值均为最低，表明本文模型在多次实验后预测误差仍最小，且集成模型比单一模型的预测精度高。HDL 模型在3 个站口各个方向的MAE平均值为5.450辆·(20 min)-1。

表4 5种模型对8 d工作日的平均预测误差Table 4 Average prediction error of five models for eight working days

2.4.2 十一国庆假日交通流预测结果

表5为考虑空间、时间、天气特征的HDL 模型对3 个站口各个方向在十一国庆假日7 d(2016年10月1日-7日)的交通流预测误差。

表5 HDL模型对十一国庆假日7 d的预测误差Table 5 Prediction error of HDL model for seven days during National Day

为评估模型的稳定性，表6给出5 种模型对十一国庆假日7 d(2016年10月1日-7日)的平均预测误差。

由表6可知，预测高峰期(十一国庆期间)交通流时，本文所提HDL 模型的MAE和RMSE 在3 个站口各个方向上的平均预测误差值均为最低，同样表明本文模型在多次实验后预测误差仍最小，且集成模型比单一模型的预测精度高。

表6 5种模型对十一国庆假日7 d的平均预测误差Table 6 Average prediction error of five models for seven days during the National Day

为验证天气等外部因素对当前道路交通流变化的影响，给出4 种典型深度学习模型在结合时间、空间及天气因素下(MF)，在3 个站口各个方向上对8 d工作日(2016年10月10日-17日)和十一国庆假日7 d(2016年10月1日-7日)的平均预测误差，如表7和表8所示。

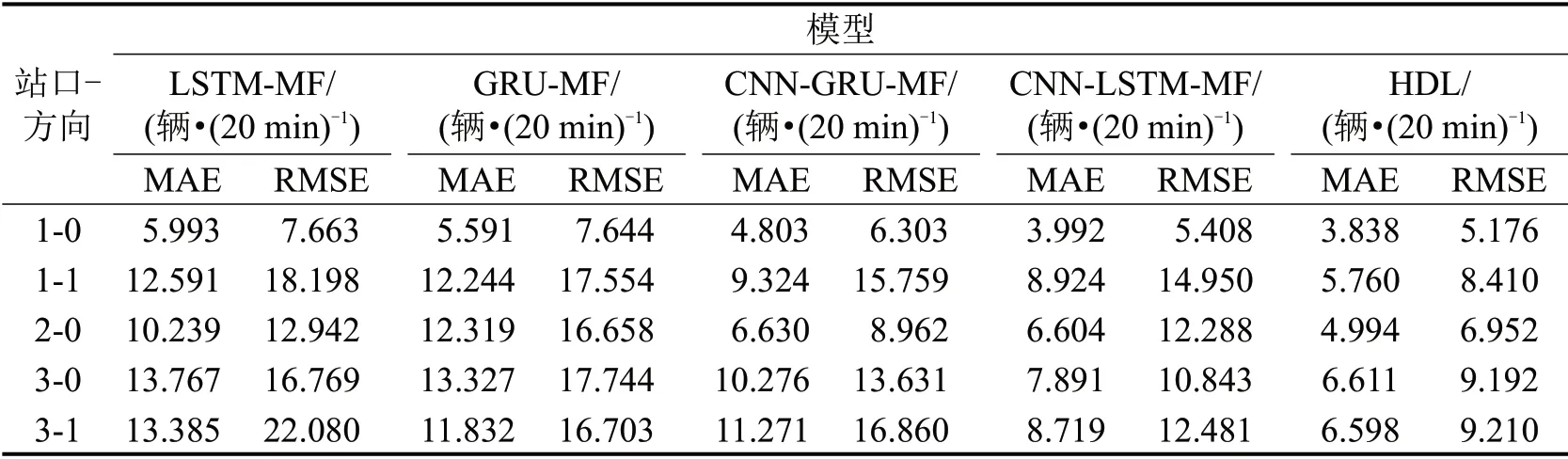
表7 加入外部因素后工作日期间5种模型的预测误差比较Table 7 Comparison of prediction errors among five models of working days after adding external factors

表8 加入外部因素后十一国庆期间5种模型的预测误差比较Table 8 Comparison of prediction errors among five models of during the National Day after adding external factors

通过表4和表7、表6和表8的对比发现：考虑天气等外部因素后，集成模型的预测精度都有所提高，但总体来说本文所提HDL 模型的预测精度仍高于其他模型。预测工作日交通流时，CNNLSTM 模型、CNN-GRU 模型的预测精度最大分别提高3 辆·(20 min)-1、6 辆·(20 min)-1。预测十一国庆期间交通流时，CNN-LSTM 模型、CNN-GRU模型的预测精度最大分别提高1 辆·(20 min)-1、5 辆·(20 min)-1。考虑多因素后，单一模型LSTM和GRU的预测精度下降，原因是单一模型无法捕捉多个特征的信息。

因此，无论是在工作日还是高峰期，集成模型的预测误差都要小于单一模型，且本文所提HDL模型对高速公路交通流的预测精度明显优于其他4种典型深度学习模型。由于国庆假期数据量远少于工作日的数据，且国庆假期交通流变化的不可控因素更多、波动较大，故国庆假期交通流的预测精度低于工作日。

为充分体现本文交通流预测效果，表9给出近两年有关交通流预测结果的对比情况。

表9 现有文献对交通流的预测结果Table 9 Prediction results of traffic flow in existing literature

文献[8-9]考虑了交通流的时空因素，但未考虑天气等因素对交通流变化的影响；文献[10-11]只考虑了交通流的时间特征，未考虑空间及天气等因素对交通流变化的影响，故其预测精度都低于本文HDL 模型。再次说明，考虑多种因素可以提升高速公路交通流预测精度。

3 结论

精准地预测高速公路交通流，不仅可以为高速公路管理人员提供决策辅助，还可以为公众出行路线选取提供参考，便于车辆分流，进而缓解高速公路交通拥堵状况。为更准确地预测高速公路交通流，本文提出一种集成深度学习模型，该模型考虑高速公路交通流数据的周期性和趋势性特点，发挥了CNN 对空间特征提取，LSTM和GRU 对长期依赖性特征提取的优势来实现预测过程，并采用某省某高速公路2016年9月19日-10月17日的数据进行模型验证。首先，为因势利导，将交通流数据分成工作日和十一国庆假期两部分分别进行训练和预测，利用滑动窗口方法，以数据的周期性特点确定了最佳窗口大小为7 d；其次，构建包含时间、空间和天气的特征矩阵作为模型的输入；再次，利用训练数据对HDL模型进行训练；然后，利用测试数据对训练好的模型进行测试同时评估该模型；最后，将本文所提HDL 模型和CNN、LSTM、CNNLSTM、CNN-GRU这4种典型的深度学习模型进行对比分析，同时将本文预测结果与近两年有关交通流预测文献进行对比。结果表明：集成深度学习模型对交通流的预测结果要优于单一深度学习模型；本文提出的HDL 模型，由于综合考虑了时空及天气因素，其交通流的预测精度明显高于其他模型，同时也体现出天气对交通流有很大影响，是预测交通流不可忽略的因素。

在未来的研究中，我们将探讨更多可能影响交通流预测性能的因素，例如探讨车辆的行驶速度、腹地城市人口与经济情况等因素，以期进一步提升高速公路交通流的预测精度。