船闸运行状态下闸门及支承运转件敏感区应力关系研究

刘明维，徐光亮*，吴林键，赵殿鹏，李明龙

(1.国家内河航道整治工程技术研究中心，重庆交通大学，重庆 400074；2.水利水运工程教育部重点实验室,重庆交通大学，重庆 400074；3.浙江省交通工程管理中心，杭州 311215)

支承运转件在闸门运行过程中发挥着重要作用，主要包括顶枢、底枢以及蘑菇头等部位。在实际的运行过程中，常会出现顶枢轴面和底枢蘑菇头磨损、底枢润滑不良、蘑菇轴头发生位移等运行故障，进而导致闸门卡阻问题[1]，影响船闸的通航。由于支承运转件部分处于水下的复杂环境，不便于直接检测，研究在运行状态下闸门及支承运转件敏感区的应力关系对于支承运转件的受力特征判断具有重要意义。

国内外学者关于闸门及支承运转件受荷响应问题进行了相应研究。王鑫等[2]以实际船闸工程为基础，建立船闸输水系统整体模型，结合船闸门叶、支承运转件等结构的布置和系统的水力特性，研究中水头闸底长廊道侧支孔船闸输水系统优化布置方案；陈一梅等[3]运用底枢摩擦副磨损试验以及实际调查数据，分别建立了底枢运行可靠性特征量的计算模型，提出了基于威布尔分布的底枢可靠性指标计算方法；叶雅思等[4]针对大源渡二线船闸人字门的背拉杆施加预应力和振动问题进行了三维有限元数值计算；李然[5]通过采集闸门关键部位的振动信号,分析其故障特征信号的特点,提出闸门顶枢状态监测及故障诊断方法；赵新泽等[6]利用ANSYS Workbench对闸门底枢的接触应力进行仿真计算，获取了轴瓦衬套、蘑菇头不同部位接触应力大小、位置、分布计算结果；周紫嫣等[7]对受闸门自重和外载荷时的接触应力计算公式进行推导，再利用ANSYS软件对闸门底枢蘑菇头受自重和外荷载时的接触应力分布进行有限元分析，将理论计算结果和有限元结果进行比较。Singh等[8]通过数值模拟方法分析闸门的受力状态，计算了不同流体域对闸门固有频率的影响；Giorgio[9]、Palanisamy[10]、Ashraf[11]、Bocchetti[12]、Dasic[13]、Bocchetti[14]等人将回归分析、人工神经网络、风险分析等技术应用于磨损失效设备的可靠性研究中，利用试验数据建立底枢磨损的可靠性模型进而对设备的磨损趋势和寿命进行预测。

国内外学者对船闸闸门及支承运转件的受荷响应问题开展了相应的研究工作。然而，已有研究大都只针对于闸门门叶或支承运转件的局部位置开展工作，闸门和支承运转件是一个整体结构，在对其受荷响应分析的过程中应把它们作为一个整体系统来进行研究，但与之相关的内容暂未在已有文献中被提到。此外，在船闸运行过程中，闸门门叶上的状态参数容易获得，但其底枢及蘑菇头等部件常处于复杂的水下环境，其状态参数难以获取，能否通过闸门门叶的受力响应特征来间接评估顶枢、底枢、蘑菇头等支承运转件的运行状态，这个问题在已有文献中未被涉及，值得深入研究。

针对以上问题，本文基于有限元数值模拟方法，通过建立船闸闸门和支承运转件的三维整体模型，研究其敏感区域在不同水位、不同闸门开度下的应力响应。根据门叶及支承运转件敏感区的应力响应参数，建立闸门门叶和支承运转件在不同工况下敏感区之间的应力响应关系，实现由闸门门叶的受力情况来间接判别支承运转件的运行状态的目的，为闸门及支承运转件的智能监测、故障预警提供了技术支撑。

1 船闸闸门概况

某船闸采用主横梁式平面人字闸门，单扇门叶尺寸(宽×高×厚)为20.2 m×23 m×3 m，双扇门重量(含门上附件加埋件)为1 210 t，共有15根主横梁；门轴柱和斜接柱截面形式采用开口式，门背后设有4根背拉杆，背拉杆截面尺寸为300 mm×40 mm。下闸首闸门的门槛高程是294.56 m(黄海高程)，上游的最高通航水位308.78 m，下游最低通航水位299.06 m，整体设计水位差9.72 m。顶枢轴直径0.28 m，A、B杆两端的直径为0.5 m，底枢蘑菇头的直径为0.9 m，衬套直径1.8 m。

2 船闸闸门及支承运转件三维模型

2.1 模型建立

根据上述船闸工程下闸首闸门的实际尺寸，建立闸门和支承运转件的三维模型，如图1所示。

图1 闸门模型Fig.1 Gate model

2.2 模型参数和计算工况

船闸闸门所用材料主要包含4类：顶枢结构采用45#锻钢(包括顶枢轴)，闸门门叶采用常规的材料Q235B钢，底枢的轴瓦采用锡青铜(ZQSN6-6-3)，底枢半球形蘑菇头采用40Cr钢，各材料参数详见表1。在进行不同工况下的数值计算时，假设闸门门叶以及支承运转件的变形均在线弹性范围内，即计算采用“各项同性弹性模型(Isotropic Elastic)”本构模型。

表1 闸门各部件的材料参数Tab.1 Material parameters of gate components

如图2所示，为了合理地模拟闸门的受力响应特性，根据闸门上下游的通航水位差，闸室水位差拟定为10 m，距离门槛4.5 m处为下游通航水位，拟定此处的相对水位为H=0 m，以0.5 m的水位增量累增至10 m，水位的工况分别为：H= 0 m、0.5 m、1 m、1.5 m、2 m、2.5 m、3 m、3.5 m、4 m、4.5 m、5 m、5.5 m、6 m、6.5 m、7 m、7.5 m、8 m、8.5 m、9 m、9.5 m、10 m；在开启过程中，闸门绕门轴柱一共要旋转67.5°，在某一水位下，每旋转7.5°便计算其结构受力状态，闸门开度的工况为：θ= 0°、7.5°、15°、22.5°、30°、37.5°、45°、52.5°、60°、67.5°。

2-a 水位 2-b 闸门开度图2 工况示意图Fig.2 Schematic diagram of working conditions

2.3 接触设置和网格划分

闸门三维模型接触分为两种：Bonded(绑定)和Frictional(摩擦)。顶枢轴面和蘑菇头面的接触形式采用Frictional，摩擦系数均为0.1，其余接触面均采用Bonded。采用Solid187(四面体单元)实体单元对闸门和支承运转件的三维模型进行网格划分，单个网格尺寸边长为：门叶结构尺寸为300 mm，其余部分采用100 mm。模型的接触设置及网格划分见图3。

图3 接触和网格划分Fig.3 Contact and mesh division

表2 约束情况表Tab.2 Constraint conditions

2.4 约束与载荷

模型中的底枢、顶枢均采用固定式，即固定在基座上，没有转动和平动。闸门在灌泄水过程中有水位的变化，闸门静止不动，限制蘑菇头底面、顶枢两个端面以及门中缝X、Y、Z三个方向的平动自由度，以及绕X、Y、Z转动自由度；当闸门在启闭时，限制蘑菇头底面、顶枢两个端面的六个自由度。施加的荷载为静水流体荷载和自重，流体荷载施加在模型与水接触的结构面上，详见图4-a、4-b；重力加速度采用ANSYS Workbench默认值，详见图4-c。

2.5 简化力学模型验证

为了验证数值模型的精度，将闸门和支承运转件整体结构简化成杆系结构，利用结构力学基本理论对简化的杆系结构进行求解。

简化模型图5所示，作用在闸门门叶上有两个荷载，分别是门叶自重和静水压力。将自重简化到门轴柱的中心上，产生一个集中力G和一个弯矩MG；将静水压力简化到门轴柱处同样会产生一个集中力F水和一个弯矩M水。通过理论计算，左、右支座反力均为15 797.3 kN，有限元数值计算左支座的反力为14 484.5 kN，右支座的反力为17 293.2 kN。二者支座反力的相对误差分别为9%和9.5%，且方向相同，验证了基于有限元数值仿真方法计算结果的正确性。

3 结果分析

3.1 结构变形及应力云图

通有限元数值仿真计算，分别得到在不同水位、不同闸门开度下的闸门和支承运转件的应力响应云图，如图6～图9所示。

由图6可知：在灌泄水水位为10 m时，门叶上最大应力处位于门叶面板的右下靠近底枢结构的位置，且随着水位的增大而增大，位置几乎不发生移动；主横梁中应力最大的是位于底部的底横梁，应力敏感区则主要集中在底横梁的左侧的上下表面上，其他横梁应力值较大处均在靠近门中缝的右侧上表面处。

在闸门实际运行过程中，顶枢轴、蘑菇头面的磨损和润滑不良等状况会使闸门产生运行故障，如图7～图9所示。顶枢的敏感区主要位于轴杆的表面下段，底枢蘑菇头面敏感区是球心到边缘中间的小椭球面，底横梁的敏感区主要处于上下表面临近门轴处。顶枢轴面敏感区的应力最大值随水位的增大而增大，应力云图的颜色逐渐加深；蘑菇头面敏感区应力值随闸门开度的变化较小，但应力最大值出现的区域随闸门开度而发生改变，且与门叶的旋转方向相同，这和实际情况相符合；底横梁敏感区的位置没有随水位的增大而发生变化，应力值随闸室水位差的增大而增大。下闸门顶枢轴面和蘑菇头球面应力最大值在各工况下分别为21 MPa和95 MPa，均没有超过最大许用应力。

3.2 结构应力结果分析

根据数值仿真计算得到的结果，对闸门门叶、顶枢、蘑菇头上的敏感区域的应力值进行数据统计，建立敏感区域的结构等效应力平均值、最大值、最小值随工况条件的变化规律。

3.2.1 应力在灌泄水过程中的变化规律

从图10～图11中可以看出：随着闸室水位的升高，上闸门的底横梁应力值呈现下降的趋势，下闸门底横梁的应力值在增加，两者的最大值、最小值、平均值均呈现相同的变化趋势；上闸门顶枢的应力值随水位的变化不明显，应力值在43 MPa左右，下闸门顶枢的应力值在水位差达到7 m之前有小幅度的上下波动，之后呈现陡升的趋势；上、下游的底枢应力值变化幅度均不大，下游底枢应力的最小值随着水位差的增加而增大。

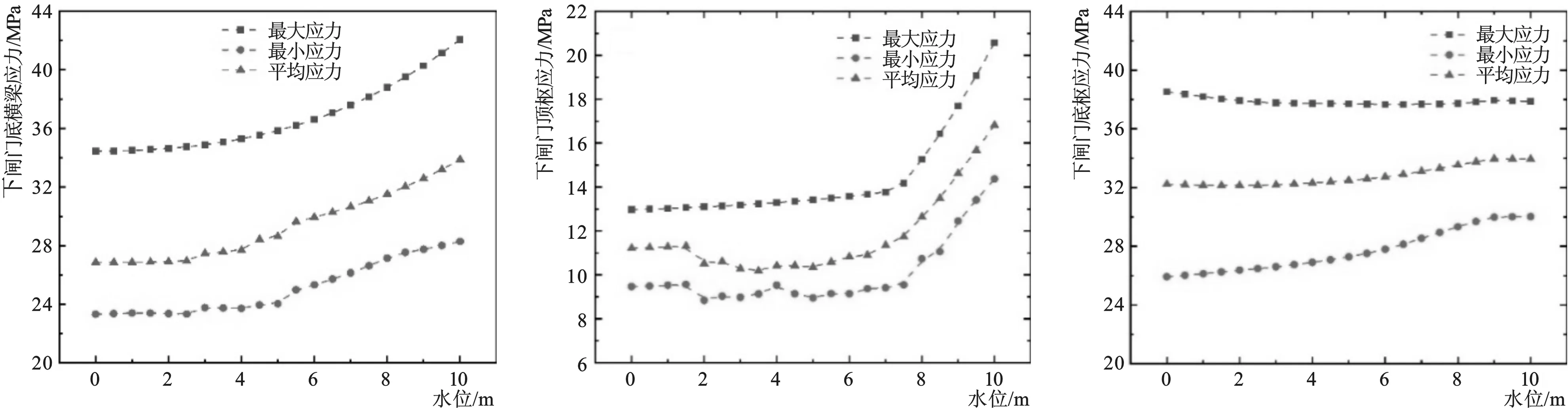
综上所述，闸门顶枢的应力值上下游呈现相反的趋势，因为在闸室水位上升过程中，导致上闸门两侧水位差减小，减小了静水压力对闸门结构变形的影响，而下闸门两侧的水位差的逐渐增大导致了水流压力增大，闸门两侧的应力差引起了结构变形的增大；从应力的大小来看，上闸门的应力水平均要高于下闸门，因为上游的水位高于下游的水位，水流压力对结构的影响更大。

3.2.2 应力在启闭过程中的变化规律

从图12～13中可以看出：上下闸门底横梁和顶枢应力出现随闸门开度的增大而减小的趋势。在下降过程中，下闸门底横梁、上闸门顶枢、下闸门顶枢的应力分别在37.5°、52.5°、30°的闸门开度处产生了应力增大现象；上下闸门的底枢的应力在各个旋转跨度下，保持平稳不变的趋势。

蘑菇头是一个旋转对称结构，在闸门开度不断增大的过程中，闸门两侧的水压力相互抵消，蘑菇头和闸门的几何中心位置保持不变。因此，蘑菇头的应力数值几乎没有变化；而顶枢和闸门的相对位置发生变化，它们的应力值随闸门开度的增大而减小。

3.2.3 闸门门叶和顶枢、底枢之间的应力响应关系

不同的水位变化、不同的闸门开度都会引起闸门和支承运转的应力的变化，通过数值模拟计算得到的结果，可以得到闸门门叶敏感区的应力和顶枢、底枢蘑菇头敏感区域的应力值之间的在不同工况下的响应关系。

上闸门门叶和支承运转件在灌泄水过程中敏感区的平均应力关系及其拟合函数如图14所示。

15-a 门叶-顶枢15-b 门叶-底枢

上闸门和支承运转件在水位变化下的平均应力关系公式如下

σ=e4.17-0.024△H+0.000 38△H2

(1)

(2)

上闸门门叶和支承运转件在开启过程中敏感区的平均应力关系及其拟合函数如图15所示。

上闸门和支承运转件在启闭过程中的平均应力关系式如下

(3)

σ=472.76+0.888sin(π(θ+4 065.44))

(4)

下闸门门叶和支承运转件在灌泄水过程中敏感区的平均应力关系及其拟合函数如图16所示。

下闸门和支承运转件在灌泄水过程中的平均应力关系式如下

(5)

(6)

下游闸门门叶和支承运转件在启闭过程中敏感区的平均应力关系及其拟合函数如图17所示。

下闸门和支承运转件在启闭过程中的平均应力关系式如下

(7)

(8)

4 结论

(1)本文建立的船闸闸门和支承运转件整体三维模型和简化理论模型的支座支反力二者相对误差在10%范围内，验证了闸门和支承运转件三维有限元模型的精度。

(2)在实际的船闸闸门中，上闸门的尺寸一般要小于下闸门的尺寸，本文假设上下游闸门尺寸一致，模拟其应力响应特性；由于尺寸一致且上游水位较高，导致了上闸首的应力值水平普遍大于下闸门的应力值水平。

(3)根据有限元数值计算结果，确定了闸门和支承运转件的敏感区位置，基于结构敏感区的应力结果统计值，获得了闸门及支承运转件敏感区应力统计值随水位及闸门开度的变化规律。

(4)建立了上下游闸门在不同工况下的闸门门叶和支承运转件在敏感区内应力的定量关系，初步实现了通过闸门的受荷响应应力值来间接评估支承运转件受力特征的目标，预判闸门支承运转件的运行故障。研究成果可为运行状态下船闸闸门的智能监测、安全预警等提供技术支撑。