一种基于可解释神经网络模型的压缩机功率软测量方法

2021-06-29王煜林周登极郝佳瑞黄大文

上海交通大学学报 2021年6期

王煜林，周登极，郝佳瑞，黄大文

(上海交通大学机械与动力工程学院，上海 200240)

压缩机是燃气轮机中的主要耗能部件.为实现压缩机组的能耗监测、提升压缩机组控制策略，需要对其功率进行准确、实时的测量.压缩机功率测量依靠扭矩仪实现，其造价高昂且大型扭矩仪尚未实现国产化.同时，为压缩机安装扭矩仪将增加压缩机的轴系长度，降低系统的可靠性.因此，目前大多采用软测量技术对压缩机功率进行计算.

软测量是指对于系统中难以测量的重要变量，选择一组既与该变量有密切联系又容易测量的二次变量，通过构造某种数学关系实现对该变量的估计[1].软测量方法的研究目前有两种方向，一种基于机理，一种基于数据.基于机理的软测量方法研究目标系统的结构及其运行过程，并通过机理公式搭建目标变量的计算模型以实现对变量的估计.早在2005年便有研究通过对滑片式压缩机的结构和受力过程进行分析，对其功率软测量模型进行改进[2].近年来的研究通过分析不同工况下压缩机的机理公式，已将其功率测量的相对误差降低至2.74%[3].上述测量方法的优势在于其普适性，对于任意系统，只要明确参数的计算机理，便可以对该参数进行测量.但其计算速度较慢，其预测难以具备实时性.同时，由于实际生产中的多种环境扰动，机理模型的准确率往往较低.

基于数据的软测量方法直接根据系统的输入输出搭建机器学习模型，并使用已有数据对模型进行训练拟合，从而使模型具备对未知输入的预测能力.文献[4]中提出一种使用等度量映射算法的软测量建模方法.文献[5]中使用改进的径向基(RBF)神经网络搭建软测量模型对污水中的化学需氧量进行计算，并将测量的相对误差降低至1.25%以内.相比于基于机理的方法，基于数据的软测量方法拥有更高的准确率和计算效率，其无需具备对象的先验知识，而根据对象的输入输出直接建模，在解决高度非线性和严重不确定性系统的测量上具有巨大潜力[6].但是，机器学习模型本身对数据集的依赖程度较大，模型的准确率极大程度上取决于数据集的泛化能力，而许多工业系统中由于生产需要、测量手段单一等问题，高泛化性的数据集往往难以获取.对数据集较大的依赖性限制了基于数据的软测量方法在较多场合的应用.

为弥补两种软测量方法的不足，文献[7]中提出一种融合机理模型和数据的软测量方法，其使用机理模型对目标参数进行计算，并使用神经网络作为补偿器对测量结果进行矫正，取得了优于机理模型的测量结果.然而，由于该方法中的主要计算模块仍为机理模型，其运行效率并未得到有效提高；同时，由于该方法的结果仍然依赖于神经网络的矫正，虽然能够在一定程度上降低软测量对数据集的依赖程度，但其准确率仍然低于传统基于数据的软测量方法.

基于以上研究现状，本文提出一种基于可解释神经网络的压缩机功率软测量方法，将机理关系预置于神经网络之中，不但能使软测量模型具备神经网络模型的快速性以及准确性，而且能降低模型对数据集的依赖程度.在对压缩机功率的测量中，搭建3种软测量模型，分别为反向传播(BP)神经网络模型和两种融入不同程度机理的可解释神经网络模型，并对比三者在不同泛化能力数据集上的表现，验证了可解释神经网络模型在压缩机功率测量上的有效性.

1 BP神经网络模型搭建

BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络，亦是应用最广泛的神经网络之一.逆向传播算法可参考文献[8],本文仅对网络前馈结构进行简述.

一个多层BP神经网络前馈结构包括输入层、输出层和若干隐藏层.每层的任意节点和下一层的所有节点相连，连接权重组成权值矩阵w.网络相邻两层之间的前向传递关系如下式所示：

(1)

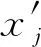
BP神经网络的输入、输出根据实际系统的输入、输出参数确定.实验中，测得5组与压缩机功率PC相关的二次变量分别为压缩机转速n, 压缩机进口温度Tin，压缩机出口温度Tout，压缩机进口压强pin，压缩机出口压强pout，作为神经网络的输入.

根据模型的输入、输出，搭建BP神经网络模型.将该模型作为模型A，其结构如图1所示.

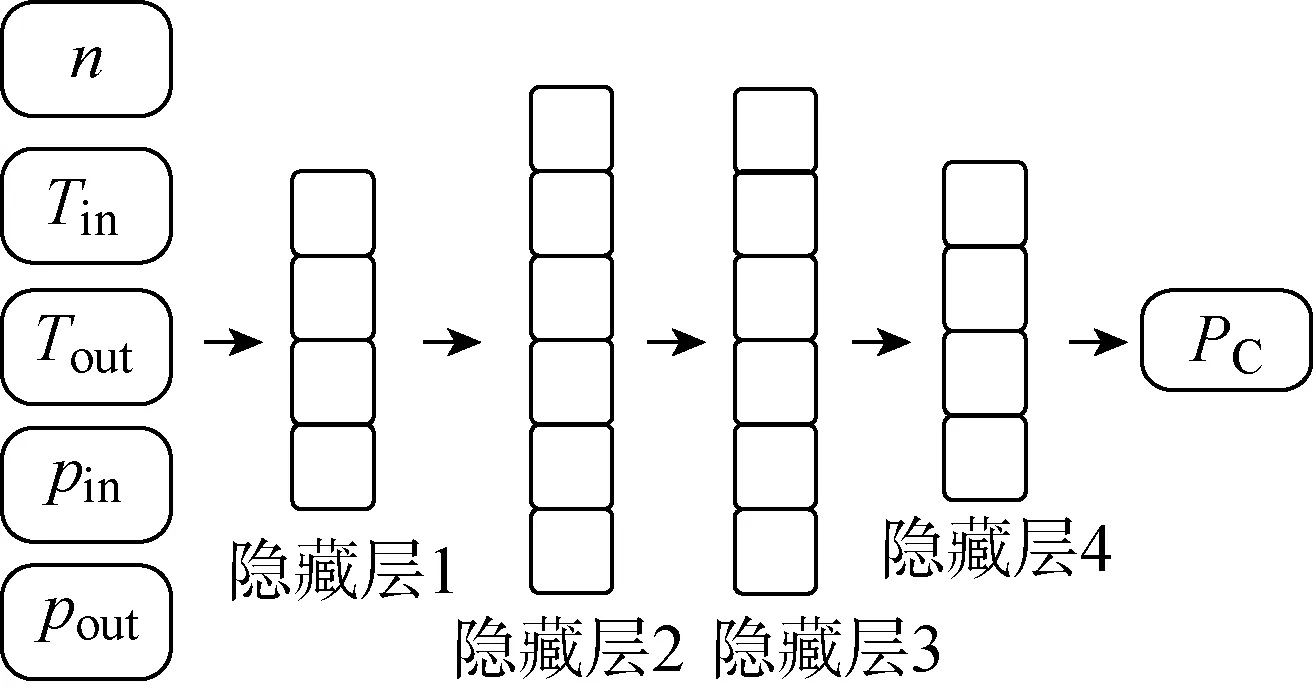
图1 模型A前馈结构Fig.1 Feed-forward structure of Model A

2 融入机理的BP神经网络模型搭建方法

机理BP神经网络模型的搭建在模型A的基础上进行，并融入压缩机的部分机理公式.根据能量守恒可知，若压缩机损耗不计，压缩机功率等于压缩机中气体质量流量和单位质量气体焓增的乘积，则有：

PC=qm(hout-hin)

(2)

式中：qm为压缩机气体质量流量；hin为压缩机进口气体比焓；hout为压缩机出口气体比焓.

气体质量流量取决于压缩机转速和入口气体的热力学状态.因此，可以得到如下函数关系f1：

qm=f1(n,pin,Tin)

(3)

压缩机中单位质量的气体焓增取决于进出口气体的热力学状态，气体的热力学状态可由气体的温度、压强、比体积中任意二者决定.因此，可以得到如下函数关系：

hout-hin=f2(pin,pout,Tin,Tout)

(4)

Δh=hout-hin

(5)

PC=f1(n,pin,Tin)f2(pin,pout,Tin,Tout)

(6)

根据式(6)在神经网络模型中融入乘法运算，搭建可解释神经网络模型，作为模型B，其网络结构如图2所示.

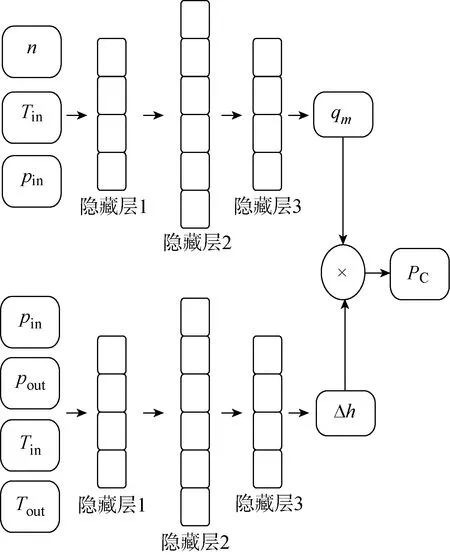
图2 模型B前馈结构Fig.2 Feed-forward structure of Model B

上述可解释神经网络模型由两部分组成，一部分以转速、压缩机进口气体的温度、压力作为输入，计算压缩机中的气体流量；另一部分以压缩机进出口气体状态作为输入，计算压缩机中单位质量气体的焓变.将这两部分计算结果相乘并作为模型最终的输出.

由于压缩机在实际运行过程中，其损耗不可忽略，引入压缩机效率ηC，可表示为

ηCPC=qmΔh

(7)

压缩机的运行效率ηC可由压气机的压比πC和折合转速nC确定，详细推导过程参考文献[10]，可表示为

(8)

(9)

可以得到如下函数关系：

ηC=f3(πC,n,Tin)

(10)

压缩机功率计算公式可改写为

(11)

依照上述机理，在模型B中增加效率计算模块，得到模型C，其结构如图3所示.

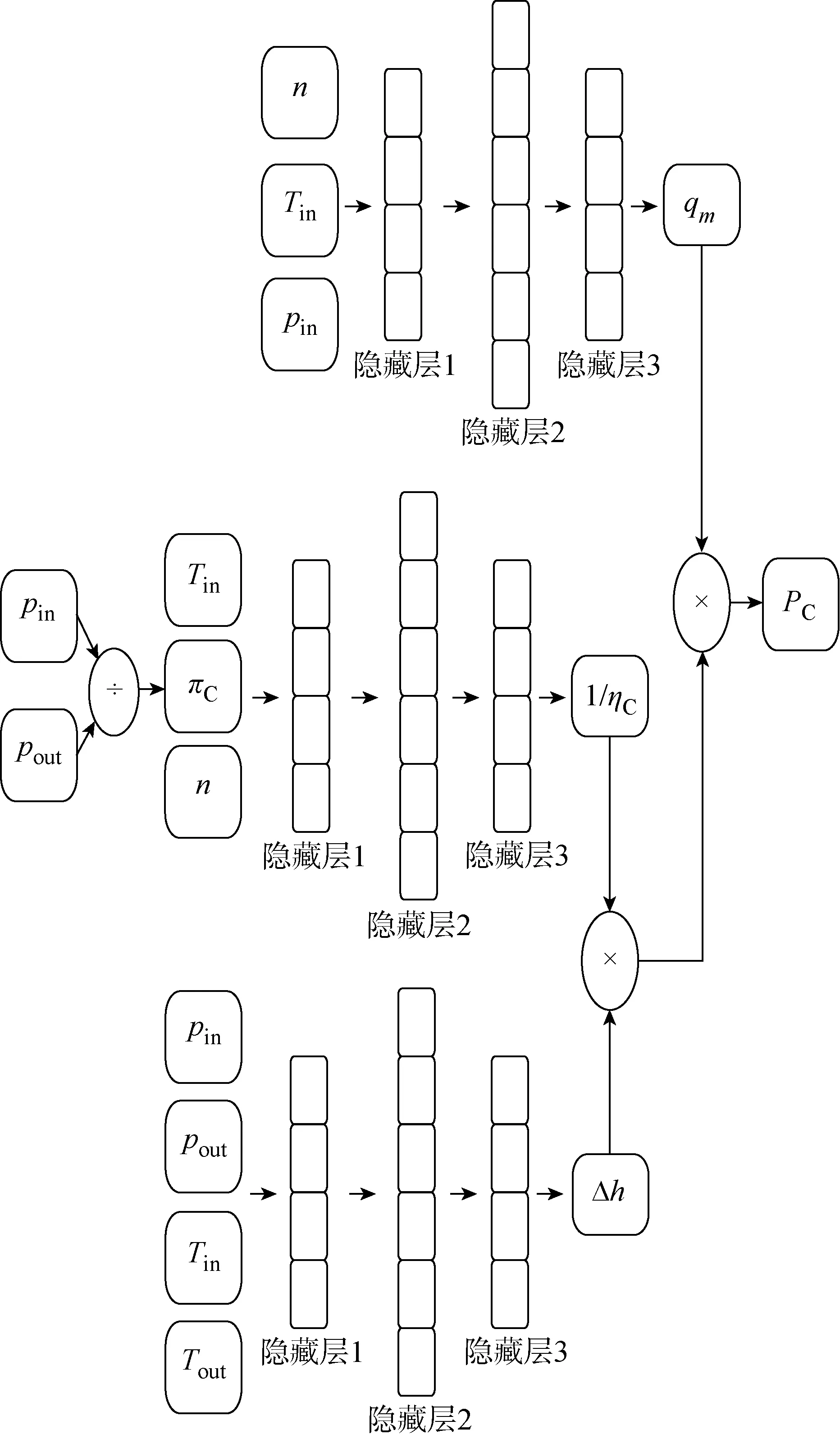
图3 模型C前馈结构Fig.3 Feed-forward structure of Model C

相比于模型B，模型C新增了一部分网络结构，用于计算压缩机的效率.该部分网络将pin、pout整合为压比，与Tin、n共同作为输入计算得到效率.由于反向传播过程中除法的求导过程较为繁琐，令该部分网络计算效率的倒数1/ηC，并将其结果和qm、Δh相乘，最终获得压缩机的输入功率.

综上所述，实验中搭建了3种软测量模型.其中，模型A为BP神经网络模型；模型B为融入少量机理的可解释神经网络模型；模型C为融入较多机理的可解释神经网络模型.

3 实验设计

实验数据来源于一台PCL803型号压缩机.采用美国KOP-FLEX高性能扭矩仪联轴器，连接于动力涡轮和压缩机中间，用于功率测量.实验中，令压缩机持续运行8.5 h，每隔1 s进行一次功率采样，并记录相应的压缩机转速、进出口温度及压力.实验共测得 30 602 组时序数据.数据集中，PC随时间t的变化曲线如图4所示.

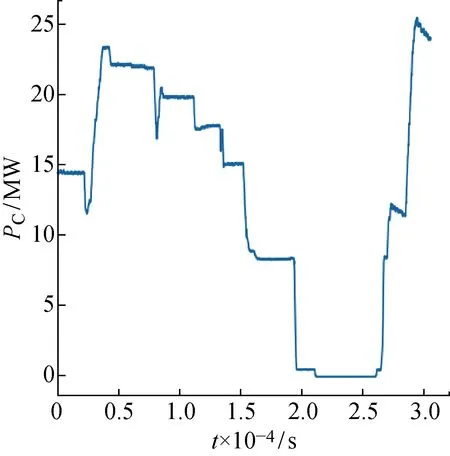
图4 数据集中压缩机功率随时间的变化曲线Fig.4 Compressor power versus time in dataset

首先，使用前2.1×104个时间节点的数据(以下简称为数据集(D)1)作为训练集训练模型A、B、C，并对后 9 602 个时间节点的功率进行预测.数据集1作为训练集几乎包括了所有可能产生的功率数值，能够保证数据集的泛化能力.该组研究的目的在于验证机理BP神经网络模型的有效性，同时为可解释神经网络模型在泛化性较差数据集上的预测结果提供对照.

降低数据集的泛化能力，仅使用前1.8×104个时间节点的数据(以下简称为数据集2)作为训练集训练模型A、B、C，以验证可解释神经网络模型在泛化性较差数据集上的有效性.实验中，设定训练簇大小为300，最大迭代次数为400，采用Adam算法[11]对模型进行优化，以模型在验证集上的误差趋于稳定作为收敛依据.采用均方根误差(RMSE)，平均绝对误差(MAE)作为模型准确率评价依据.其计算公式如下所示：

(12)

(13)

表1 模型参数设置Tab.1 Setting of model parameters

4 结果分析

模型A、B、C在数据集1和2上的拟合及预测结果如图5～7所示；表2所示为压缩机输入功率预测值.由于数据集1的泛化性良好，A、B、C模型在数据集1上具有相似的、良好的表现，其均方根误差、平均绝对误差均在1%以下.其中，模型C在测试集上的均方根误差为0.94%，相比模型A降低了1.1%；平均绝对误差为0.49%，相比模型A降低了41.0%.3种模型的功率预测曲线和实际曲线基本重合，仅在某些功率突变的时间段内有小幅度的偏离.

表2 压缩机输入功率预测准确率Tab.2 Accuracy of input power prediction of compressor

图5 模型A在D1和D2上的训练及其预测曲线Fig.5 Training and prediction curves of Model A on D1 and D2

而在泛化性较差的数据集2上，模型A、B、C的预测偏差均有一定程度的增加，但模型B和C具有远好于模型A的预测表现.其中，模型C在测试集上的均方根误差为1.28%，相比模型A降低了79.8%；平均绝对误差为0.73%，相比模型A降低了86.1%.而对于仅融入较少机理的模型B，其表现虽然不及模型C，但也展现出远好于模型A的预测能力.在实际预测曲线上也可以看到，模型A在预测1.9×104～2.7×104时间段以及2.9×104～3×104时间段内的功率变化时产生了较大的偏差，而模型C在各个时间段上的预测结果均良好.

图6 模型B在数据集1和 2上的训练及预测曲线Fig.6 Training and prediction curves of Model B on D1 and D2

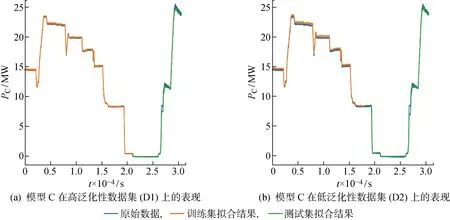
图7 模型C在数据集1和 2上的训练及预测曲线Fig.7 Training and prediction curves of Model C on D1 and D2

综合以上实验结果，认为可解释神经网络模型在使用泛化性良好的数据集训练时，具有不弱于BP神经网络模型的准确率和稳定性；在使用泛化性较差的数据集进行训练时，可解释神经网络模型相比BP神经网络模型具有更强的预测能力.基于可解释神经网络的软测量模型，不但具有传统神经网络模型的准确性和高效性，同时还降低了模型训练过程对数据集的依赖程度，是一种有效的压缩机功率软测量方法.