感性为基，融合推理

林迪 林志辉

【摘 要】《三角形的三边关系》是图形与几何领域的经典课例，现行人教版教材是众多版本 中为数不多引入公理的教材，本课尝试以活泼的情境引导学生初步了解公理，进而渗透三角形 三边关系的推导，并将公理推导融合于后续操作、探索、验证等教学活动之中，以公理为基础， 通过推理得出结论，使学生对三角形三边关系的认知更加深刻。

【关键词】三角形 三边关系 几何推理

【缘起】

人教版四年级下册的《三角形的三边关系》作为图 形与几何领域的经典课例，本课该如何突破？如何从三 边关系的角度进一步认识三角形的内涵？

笔者研读教材发现，现行人教版教材增加了 “两点 间所有连线中线段最短，这条线段的长度叫作两点间的 距离”这段表述。它是众多版本中为数不多引入公理的 教材，这与八年级教材中利用“两点间线段最短”得到性 质“三角形任何两边的和大于第三边”是一脉相承的。 教材的编写意图是为学生在小学阶段埋下几何推理的种 子，渗透几何证明思想。

通过前测，笔者发现大部分学生对于三角形三边关 系有一定的认知。但是判断“4厘米，5厘米，9厘米能否 围成三角形？ ”出错较多，学生较难想象图形。笔者尝试 基于公理“两点间所有连线中线段最短，这条线段的长 度叫作两点间的距离”引导学生进行初步的几何推理， 结合实际操作、想象、直观演示等将理性推理与直观感知 相融合，以问题驱动的方式认识三角形的三边关系，进一 步丰厚三角形的认识。笔者确定了如下教学目标：

（1）    知道三角形的三边关系，能正确判断怎样的三 条线段能围成三角形。

（2）    经历三角形三边关系的探索、发现过程，积累活 动经验，进一步发展空间观念和推理能力O

（3 ）感受数学知识之间、数学与生活间的联系，收获 成功的体验，激发数学学习的兴趣。

【实录】

_、情境激趣，引入公理

师：小狗要尽快吃到骨头，它会怎么走？为什么？

生：连接AB，走线段AB，因为这条线路最短。

师：连接AB两点的连线可以有很多条，但线段AB 是所有连线中最短的，线段AB的长度就是AB两点间 的距离。

设计意图：数学公理对处于具体运算阶段的四年级 学生而言是非常抽象的，创设“小狗啃骨头”的生动情境 能帮助学生迅速地将数学公理与问题情境联系起来，将 数学公理生活化，同化纳入自己的知识体系中。

二、变化情境，运用公理

师：在三角形ABC中，小狗想尽快吃到骨头该怎么 走？为什么？

生：走线段AB，因为两点间距离最短，AC+BOAB。 教师利用课件变化小狗和骨头的位置，继续提问： 在三角形里，小狗要尽快吃到骨头该怎么走？为什么？

设计意图：教材引入“两点间距离最短”的公理，而 三角形两边之和大于第三边作为该公理在三角形内的推 广，将两者在此环节用生活情境进行融通，使学生能有效 理解公理，同时为三角形的三边关系推理奠定了基础。 从长远来说，也是为后续严谨的几何推理奠定基础。

三、前测猜想，操作验证

（-）判断4厘米、5厘米、10厘米的小棒是否能 围成三角形

1.      直观判断

判断下面每组中的三条线段能否围成三角形

（1） 4厘米、9厘米、10厘米          （2） 4厘米、5厘米、10厘米

'亦    ：        30

8

I        直

肯圍成     耻围

（3） 4厘米、5厘米、9厘米   （4） 5厘米、9厘米、10厘米

能围成 不能围成  能围成     不能围成

师：4厘米，5厘米，10厘米三条线段能不能围成三 角形？

生：围不成，因为4+5 <10o

设计意图：学生不是一张白纸，学生是带着对三角 形的三边关系的直观理解进入课堂的，因此直接从学生 的判断情况入手，从“能不能”转化到“为什么”，引导学 生从直观的判断转化到有理有据的判断，贴合学生的学 情进行教学。

2.      操作判断

师：到底“4厘米，5厘米，10厘米”能不能围成三角 形，用小棒验证说明。

生1：围不成，因为用10厘米做底，4厘米，5厘米的 两条线段无法碰到一起。

生2： 4厘米和5厘米的小棒最靠近的时候中间还 缺了一段，没法碰到一起。

设计意图：对部分已经知晓三角形三边关系的学生， 这时的操作就不是探究结论的操作，而是验证性操作。 学生通过操作验证自己的结论，将抽象的结论与具体的 直观的操作相结合，丰厚对结论的认知。而之前无法进 行判断的学生，通过动手操作，在头脑中建立起了两边之 和小于第三边无法围成三角形的直观表象。

3.演示判断

师：想象，以10厘米为底，4厘米和5厘米两条线段 分别绕两个端点运动，越来越靠近，会不会有交点？

4厘米      ＼        /        5厘米

：10厘米

生：两条线段距离最近时还有1厘米的距离。

4.公理判断

师：现在你能说明为什么此时不能围成三角形吗？

生：如果能围成三角形，那么两边的和小于第三边， 那就不是两点间线段最短了，所以围不成。

设计意图：学生尝试用公理解释原因，让学生在具 体问题的解决情境中尝试用公理进行几何的逻辑证明。

（-）判断4厘米、5厘米、9厘米的小棒是否能围 成三角形

1.      直观判断

生：这三条线段不能围成三角形，因为4+5=9。

2.      演示验证

师：想象，以9厘米为底，4厘米和5厘米的线段分 别绕两个端点进行运动，两条线段是否会有交点？交点 在哪？

4厘米      V       弓厘米

A 9厘米

生：交点在9厘米的线段上，两条线段和底重合了。

设计意图：当两边之和等于第三边的时候，就不再 进行动手操作，而是直接通过几何画板进行演示验证。 因为实物粗细的限制，往往会给学生造成不必要的干扰， 通过想象和几何画板的动态演示，使学生更直观地理解 两边之和等于第三边时会重合或者平行，刚好不能围成 三角形。

（三）回顾课前学习单重新判断两组线段是否能围 成三角形

师：现在你觉得“5厘米，9厘米，10厘米”和“4厘米， 9厘米，10厘米”是否能围成三角形？

（四）利用公理，解释三角形的三边关系

师：三角形的三边有什么关系？

生1 ：三角形中两边之和要大于第三边。两边之和 等于或小于第三边的时候就不能围成三角形。

生2 ：“两点之间所有连线中线段最短”就是“两边 之和大于第三边”。

四、巩固提升，拓展练习

（一）  基础巩固，快速判断

师：快速判断这三条线段是否能围成三角形？说一 说为什么？

（1）    3厘米，5厘米，7厘米。

（2）    5厘米，5厘米，10厘米。

（3）    4厘米，14厘米，7厘米。

生：通过三角形两边之和大于第三边进行判断，第 一题三条线段可以围成三角形，其他两组不可以。

师：4+14>7，为什么不能围成三角形？

生：4+7<14，要任意两边之和大于第三边才能围成 三角形。

师：第三组线段，如果要换掉14厘米，换成几厘米 可以围成。

生：将14厘米换成1?10厘米都可以。

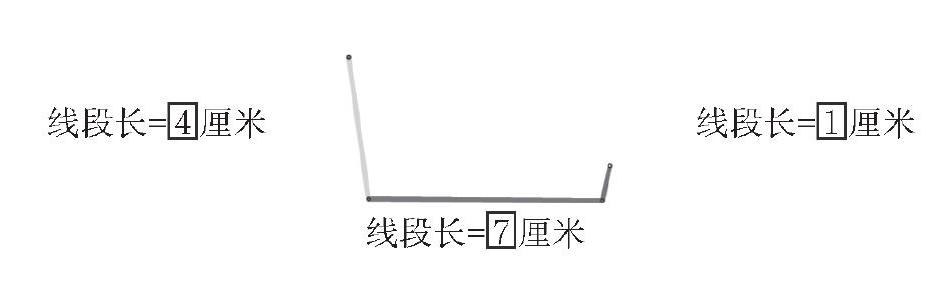
师：想象，将14厘米换成1厘米的时候，会出现什 么样的情况？

线段长=团厘米       线段长=日厘米

I

线段长=回厘米

设计意图：“三角形任意两边之和大于第三边”，“任 意”对四年级的学生而言理解起来是非常抽象的，因此 利用换掉其中的一条边的习题设计，在冲突中让学生自 然感受到“任意”的具体含义，让抽象的概念与具体的实 例相结合，教育自然发生。

（二）  练习提升，发散思维

师：一条长20厘米的纸条，剪两刀分成三条，第一 刀剪在什么地方，使得第二刀不论剪哪，都不能圍成三 角形？

生1 ：第一刀剪在8厘米处，8厘米、1厘米、11厘米 就不能围成1个三角形。

生2：我不同意，第二刀可以剪成6厘米，8厘米、6 厘米、6厘米，是能围成三角形的。

生3 ：第一刀剪在10厘米处，因为剩下两条边加起 来都只有10厘米，两边之和等于第三边，不论怎么剪都 不能围成三角形。

师：只能剪在10厘米处吗？

生1 ：第一刀剪在0.1厘米处。

生2 ：不同意，剩下的两边之和19.9，大于0.1，在剩 下的中间剪，可以围成三角形。

设计意图：通过基础练习，学生巩固了对三边关系 的理解，并通过换一根，让学生具体感知三角形中“任 意”两边之和要大于第三边中“任意”的含义，并通过拓 展提升，发散学生的思维，使其进一步理解三角形的三边 关系。

【反思】

一、         公理为基，推理融合

本课尝试以鲜活的情境认知公理，进而渗透三角形 三边关系的推导，并将公理推导融合于后续操作、探索、 验证等感性活动中，达到公理为基、推理融合，使三角形 三边关系的认知走向深刻。

二、         生本课堂，两个关注

本课充分体现了以生为本的教学理念，既关注学生 起点，又关注不同学生的发展。将前测数据作为课堂讨 论的核心，让学生产生思维的碰撞，又通过大问题、大环 节，给予学生大空间。如最后一题，“20厘米剪2刀，第 一刀剪哪里一定围不成三角形”的设计就是让不同层次 的学生都能伸手跳一跳，兼顾了不同学生的需要。

三、         感性为基，技术助力

实物操作有一定的局限性，引入几何画板、利用想象 打破了局限。在本设计中，学生基于不断想象，借助几何 画板的动态效果演示，直观感受三条线段围成的各种情 况。同时通过调整两条线段与第三条线段的角度，显示 两条线段的运动轨迹，达到随生调整的状态。