全自动食品售卖机机械振动控制方法

郝军，丁泽庆

1.驻马店技师学院（驻马店 463000）；2.南阳技师学院（南阳 473000）

机械振动会影响自动售货机的工作效率。为解决这个问题，科学家们通过多种方法研究如何控制振动[1-3]，如张保生等[4]设计船舶主机设备振动控制方法，根据舰船主机结构的特征，确定主机设备振动位置，为振动控制提供基础，保证其拥有更好的减振性能，具有良好实际效果；魏春岭等[5]在航天器姿态机动中，结合经典的Bang-Bang姿态机动指令和姿态跟踪控制器，实施机动路径的跟踪，形成低频柔性模态的振动抑制。但是，上述方法都是被动控制方法，主动性弱，主要依靠人工控制，能耗大，成本高。

对此，试验建立所需的滤波器形式和参数，使机动后的稳定时间等效于模态振动周期，提出一种全自动食品售卖机机械振动控制方法。

1 全自动食品售卖机机械振动理论与模型优化

当自动售货机的工作频率与外界环境相同时，会引起自动售货机的机械振动[6]。自动售货机的机械振动模型属于线弹性结构，如图1所示。

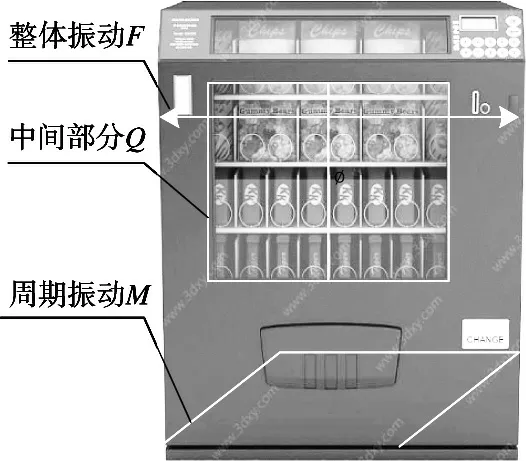
图1 全自动食品售卖机机械振动模型

图1 中，全自动食品售卖机在实际运行中，设备故障程度加剧时，由故障引起振动随之加剧且一般具有一定的周期成分，当机器振动不平衡、不对中时，全自动食品售卖机的整体振动力F增强，随机振动中的周期振动力M也会加强；与其他设备不同的是，全自动食品售卖机中间部分Q是空的，易产生共振，松动，整体不稳定性扩大，整台全自动食品售卖机机械振动力也随之增大。对此，利用牛顿第二定律计算出全自动食品售卖机机械振动模型每一个结构的受力情况，计算如式（1）。

式中：Mu为全自动食品售卖机的模态质量；Ku为全自动食品售卖机的模态刚度；Cu为全自动食品售卖机的模态阻尼；Fu为机电模型受到的阻力。

如果被控制的机械结构和压电元件共同承受振动作用[7]，那么所形成的电耦合方式不同，表示为

式中：F为全自动食品售卖机在机械振动过程中产生的力；Au为全自动食品售卖机的机械动力；I为全自动食品售卖机的机械振动损失应力。

自动售货机在运行过程中，经常会产生机械能、动能等多种能量，根据能量守恒定律，计算全自动食品售卖机机械结构电耦合方式，提高自动售货机各部件的能耗，从而达到控制自动售货机振动频率，提高控制效果的目的。

2 全自动食品售卖机结构响应分析

将自动售货机其离散化可得到自动售货机结构系统的动平衡方程[8-9]，表示为

式中：M为全自动食品售卖机的体系质量；C为阻尼；K为全自动食品售卖机刚度矩阵；为全自动食品售卖机结构体系相对地面的加速度；为全自动食品售卖机结构体系运动速度；X为位移向量，In为位移影响向量；为地面水平运动在t时刻的运动加速度。

计算全自动食品售卖机结构体系在振动的瞬时过程中，给定的初始条件，即

式中：X0为全自动食品售卖机结构体系的位移；为全自动食品售卖机结构体系的速度，利用直接积分法在时域内，获取全自动食品售卖机结构体系在t1时刻的位移和加速度等信息。利用上述计算过程，可以获取到和Xt在t时刻的参数值，从而推导出和时刻的参数值。

如果全自动食品售卖机在振动过程中的加速度在[t,t+Δt]区间内为线性变化，通过导入控制参数θ[10]，可以得到振动加速度在[t,t+θΔt]内也是线性变化。

假设0≤τ≤θΔt，根据振动过程中的加速度假设条件可以得到，全自动食品售卖机在振动过程中的加速度向量在[t,t+θΔt]范围内，可以描述为

τ=θΔt时，积分处理式（7），可以得到

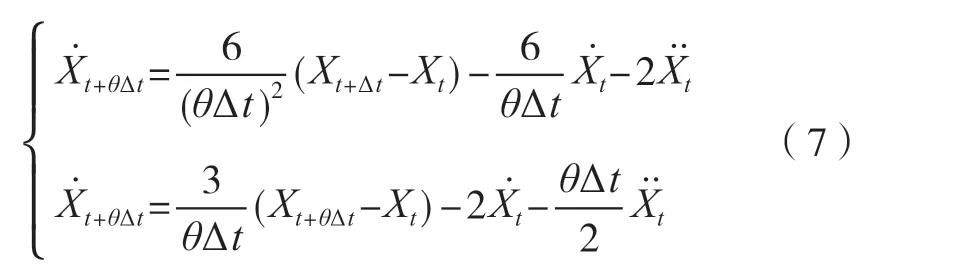
全自动食品售卖机在t+θΔt时刻发生振动时，其结构体系的动力学方程可以描述为

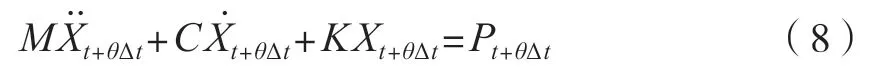
式中：Pt+θΔt为全自动食品售卖机在振动过程中的外载荷向量，Pt+θΔt=-MInxg（t+Δt）为振动等效荷载。将式（7）代入到式（8）中，可以得到一个关于Vt+θΔt的表达式，为

在全自动食品售卖机振动的频域范围内，可以对全自动食品售卖机结构体系的动力学方程进行傅里叶变换处理[11]，可以得到

式中：H(ω)为全自动食品售卖机结构体系位移相对于的频率传递函数矩阵，根据全自动食品售卖机的随机振动思想[12]，其相对位移功率密度函数矩阵可以描述为

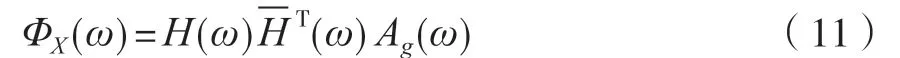
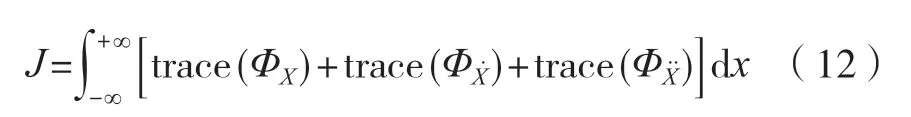
通过对自动售货机结构系统的离散化，建立自动售货机结构系统的动平衡方程。

根据给定的初始条件和全自动食品售卖机的振动原理，计算自动售货机在振动过程中的加速度，并对自动售货机结构系统的动力学方程进行傅立叶变换处理，完成自动售货机结构系统的机械振动响应分析。

3 全自动食品售卖机机械振动控制

分析自动售货机结构系统在机械振动作用下的非线性信号。采用经验模态分解方法将非线性信号分解为固有模态函数，在变换之前，假设机械振动信号的每1个采样间隔对应于1个频率值，采用Hilbert变换处理每一个固有模态函数分量yj(t)，可以得到

式中：cj(t)为第j个采样点的固有模态函数，P为柯西主值，yj(t)与cj(t)之间形成共轭时，就可以获得解析信号，即

其中，Aj(t)为第j个固有模态函数分量的信号振幅；θj(t)为相位角，i为全自动食品售卖机的结构体系层数。与解析信号Zj(t)对应的频率表示为

利用Hilbert变换可以得到全自动食品售卖机的多个固态模态函数分量[13-14]，可以将x(t)表示为

令被控制的全自动食品售卖机的机械结构具有n个自由度，在不考虑全自动食品售卖机质量和阻尼的情况下，将全自动食品售卖机结构体系的动力学平衡方程变换为

式中：Kv为全自动食品售卖机的机械结构附加刚度矩阵，Ds为机械振动作用下全自动食品售卖机的位置矩阵。通过引入状态空间[15]，将式（17）的方程还可以变换为

式中：Z为状态向量，为变换处理后的状态向量，Av为附加振幅，D为全自动食品售卖机的经过状态变换后的位置矩阵。

完成状态变换处理之后，假设将主动变刚度设备安装在全自动食品售卖机机械结构的第i层，那么在全自动食品售卖机机械结构的第i层和第i-1层之间产生控制力，那么存在

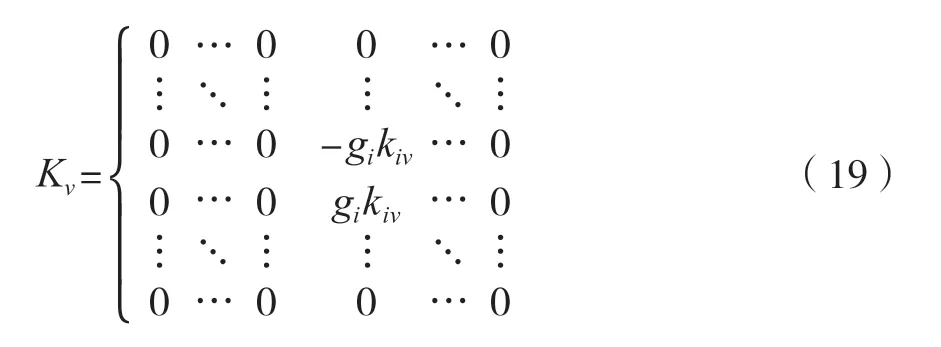
假设Pj为第j个采样间隔时间内全自动食品售卖机的振动频率参数值，为避免出现共轭现象，振动频率参数值Pj接近任何一个固有频率时，就可以通过开关函数对全自动食品售卖机的机械振动进行控制，控制过程中的切换函数为

因此，利用自动售货机的多个固态模态函数分量，对自动售货机结构系统的动力平衡方程进行变换，并结合控制过程中的切换功能，实现自动售货机的机械振动控制。

4 试验对比分析

为验证所提方法在耗电量方面的性能，分别引入文献[4]的机械振动控制方法和文献[5]的机械振动控制方法，作为对比方法，测试3种控制方法的机械振动控制耗电情况，结果如图2所示。

图2 机械振动控制耗电量对比结果

从图2的结果可以看出，文献[4]的机械振动控制方法在规定的波动周期内，机械振动在最高点的耗电量为5.75 kW·h，文献[5]的机械振动控制方法在规定的波动周期内，机械振动在最高点的耗电量为3.42 kW·h，而所提方法在规定的波动周期内，机械振动在最高点的耗电量为1.55 kW·h，因此可以得到，所提方法比其他2种方法的耗电量分别低73%和54.7%。

为验证所提方法对全自动食品售卖机机械振动的控制效果，分别引入文献[4]的机械振动控制方法和文献[5]的机械振动控制方法，测试3种控制方法的机械振动频率情况，结果如图3所示。

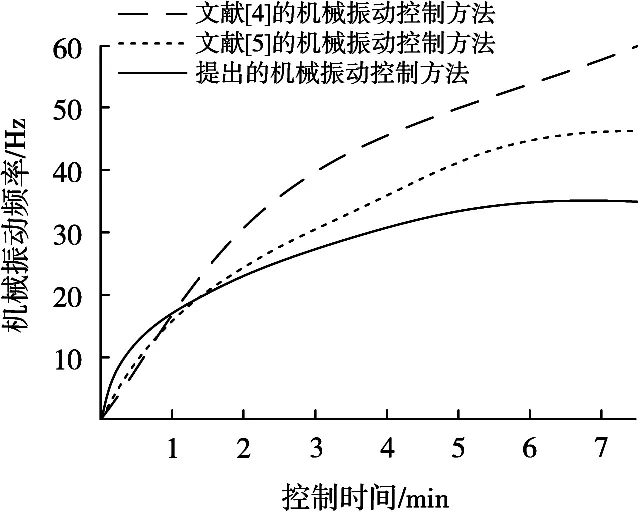
图3 机械振动频率情况

从图3的结果可以看出，机械振动控制时间1 min时，3种控制方法测试得到的机械振动频率非常接近，机械振动控制时间从第2 min开始，3种控制方法测试得到的机械振动频率越来越快，且3种方法的差距也越来越大，由此可以得出，所提方法可以有效控制全自动食品售卖机的机械振动。

3种方法的控制能耗对比情况如图4所示。

图4 控制能耗对比情况

在测试初期，3种控制方法的能耗差距就非常大，随着控制时间变化，文献[4]的机械振动控制方法得到的控制能耗最高，所提方法的控制能耗最低，因此可以得到，所提方法可以降低全自动食品售卖机的机械振动控制能耗。

综合试验结果可以看出，在相同控制时间下，所提方法的可靠性更高。

5 结语

提出全自动食品售卖机机械振动控制方法，通过建立全自动食品售卖机机械振动理论模型，对全自动食品售卖机结构体系进行响应分析，结合全自动食品售卖机机械振动控制流程，实现全自动食品售卖机机械振动的控制。结果显示，所提方法在耗电量、机械振动频率和控制能耗方面，具有更高的可靠性。