微压力表测量不确定度的评定及CMC表达探讨

黄健勇

（广东省台山市质量技术监督检测所，广东台山，529200）

0 引言

根据《计量标准考核规范》中明确提出的规定，分析评定微压力测量表的不确定度；按照《法定计量检定机构考核规范》中的内容，测量机构需要将参与项目的全部量程与参数都需要计算相应的校准测量能力。考虑到微压力测量表对于不确定度的评定与对校准测量能力的表达之间的关系较为不清晰。因此，将在实例测量、判定的基础上，对二者展开工作的过程与需求进行阐明。

1 计量标准考核中的测量不确定度

在相应的规则章程中，对微压力测量表的不确定度评定的定义是：基于计量检定规定，通过计量标准，将典型的被评定或被校准的对象进行检定后得出的不确定度。因此，在不确定度的评定中，还应将被测对象与测量影响进行纳入，且必须保证被测对象具备一定的代表性与典型性，微压力表在计量标准考核中测量不确定度的评定与常规条件下的不确定度评定具有一定的重复性，但是在实际的评定与分析中，应明确以下两点：第一，如果计量标准能够对多个参数进行测量，需要分别提供每个参数的微压力表测量不确定度评定流程；第二，如果被测对象的分度值或不确定度不同，那么需要采取的评定方式也应进行调整匹配，假设测量点之间没有较大差距，则可以提供典型的不确定评定过程，在实际的评定中，应针对项目的特征对其进行不确定度的测量[1]。

2 实验室的校准测量能力

为保证实验室或相关机构开展校准测量能力的正确评定，首要任务是明晰校准测量能力的应用含义。对于校准测量能力的定义是：向用户提供高质量的校准测量，通过因子k=2或者置信概率为p=0.95的扩展不确定度来表达。此外，在实验室中也可以将校准测量能力称作最佳测量能力。专业的欧洲认可组织对于校准测量能力的阐述是：实验室的校准测量能力在其认可标准范围内，当用于规定、实现、保存一个或多个值的测量标准处于理想状态下，并将其进行常规校准时，能够将微压力表测定不确定度降至最低；当用于测量数值的仪器处于理想状态下，并将其进行常规校准时，能够将测量仪器的不确定度降至最低。基于以上定义可知，微压力测量表的校准测量能力主要应用于特定、具体的量的测算中，即测量结果。因此，微压力表校准测量能力是求测量结果的不确定度，属于连接测量结果的参数。

从理论层面上来看，校准测量能力是实验室将不确定度最低的“理想被校”通过测量后得出的最小测量不确定度。但是，“理想被校”非常少见。为解决这一问题，通常会采取以下两种被校方式进行替代。第一种，选取稳定性与重复性强的被校来替代“理想被校”。在校准测量能力评定的过程中，将样本标准差进行归并；第二种，选取稳定性非常强并对测量结果分散性贡献只由分辨力误差产生的被校替代“理想被校”。在校准测量能力评定过程中，将不确定度的贡献部分转变为分辨力对测量结论不确定度的贡献部分。

在测量短时间的分散性贡献时，可以将量块、砝码、电阻等相对平稳的被校进行忽略。以上被校与理想被校之间的差距微乎其微。因此，可以将以上被校的校准测量能力与不确定度划等号。对于校准测量能力的表述方法与测量不确定度的评定方法相对一致。例如：当不同量程或测量点的被校结论不一致时，就不能应用同一个被校值，应根据不同分段，提供不同的校准测量能力，或给予校准能力范围，同时，提供典型量程及测量点的校准测量能力[2]。

3 微压力表测量不确定度评定和校准测量能力表达分析

3.1 标准不确定度评定

首先，确定DWRER4级的（0-60）Pa且分度值为2Pa的为微差压表为评定设备，在此基础上开展不确定度的评定工作；其次，将标准补偿式微压计产生的不确定度进行分量，并记为U1。微压计生成的不确定度分量主要由二等微压计的压力误差产生，此微压计的不确定度分量的分布是较为均匀的，符合B类不确定评定，由标准补偿式微压计产生的分量误差范围是±0.8Pa；最后，将由重复性测量产生的不确定度进行分量，并记为U2。当标准器处于30Pa状态时，对微压力表进行10次重复性试验，将十次测量结果进行平均值计算，结果为：=30.08Pa。单次的检测标准差的计算过程及计算结果如公式1所示：

而平均值的实验标准偏差的计算过程及计算公式如公式2所示：

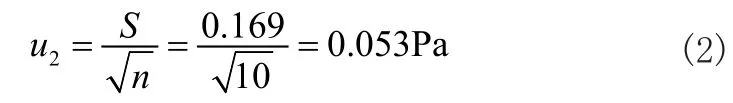
通过测量值进行估读与引入的不确定度进行分量，记为U3。遵照测量标准，对微差压表进行数值读取时，应读至标准分度值的处。结合指针深度与人工视觉误差，对于误差的估读应按照不可靠性的分度值估计。此误差的分布属均匀形态，因此，读数的标准不确定度分量的计算过程及结果如公式3所示：

考虑到重复性计算产生的误差，只保留最大的影响分量u3。

3.2 合成标准不确定度

在对合成标准的不确定度展开计算时，各个影响分量均应选取其中较大的数值。计算过程如公式4所示：

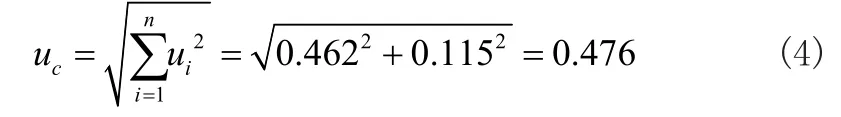
对标准不确定度的计算进行扩展时，首先需要确定k的取值，当k=2时，将不确定度扩展为：

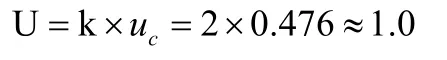
3.3 微压差计标准装置校准的不确定度评估

根据相关规程，常规校准应做到对微差压表中的全部测量点进行校准，允许误差与之前一致，且仪表的分度值的量程范围也不存在变化，从而确定不确定度的值为1.0Pa。

当校准压力表的等级与分度值出现差异时，不确定度的分量u2与u3均会出现一定的不同。考虑到仪表分度值过大导致重复性降低的原因会间接影响不确定度关于分度值的函数[3]。结合标准仪器的允许误差及校准点，可以确定：当校准点为0-1500Pa时，不确定度的表达方程为；当校准点为1500-2500Pa时，不确定度的表达方程为此公式满足规程条件，公式中d代表被校准仪器的分度值。

3.4 校准测量能力的表达

结合以上测量不确定度的评定过程与内容，DWYER微差压表是补偿式微压计标准装置的理想被校微压力表。因此，校准项目的校准测量能力为：校准点处于0-1500Pa阶段时，校准测量能力的不确定度的表达为；准点处于1500-2500Pa阶段时，校准测量能力的不确定度的表达为。

4 结语

综上研究证实，计量标准考核中，微压力表测量不确定度的评定是对典型被测对象开展校准时得出结论的不确定度，此不确定度必须具备一定程度的代表性与普遍性。校准测量能力是全部测量结果中最小的不确定度，反映的是标准条件下的最高测量水平。