迭代法求解电路方程组的Matlab软件实现

刘雄峰，姚思远

（三峡大学电气与新能源学院，湖北宜昌，443002）

0 引言

在电路课程中经常涉及到线性方程组的求解，具体的方法有精确法和迭代法，精确法求解不需要采取近似舍入，而是采用初等变换方法求出方程组的解；迭代法则是通过有限次的迭代，在允许的精度范围内求解方程组的近似解，精度要求设定越高，求解值越趋近与真实值。

1 MATLAB软件和迭代算法简介

MATLAB是美国mathworks公司出品的商业数学软件，用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境，主要包括MATLAB和Simulink两大部分；MATLAB具有高效的数值计算及符号计算功能，能使用户从繁杂的数学运算分析中解脱出来。

迭代法也称为转辗法，是一种不断用变量旧值递推新值的过程，迭代算法是用计算机解决数学问题的一种基本方法，它利用计算机运算速度快、适合做重复性操作的特点，让计算机对一组指令（或一定步骤）进行重复执行，在每次执行这组指令或步骤时，都将从变量的原值推出它的一个新值[1]。

设有线性方程组Ax=b，其中

选取x0作为方程的初始近似解，以之迭代出一个方程组近似解收敛数组(xk),k≥0。[2]即可将式（1）变为：

根据初始近似解x0，通过如下的迭代过程可以产生迭代根数组。

Pxk+1=Qxk+b,k=0,1,...，当‖P-Q‖＜0时数组收敛。

线性方程组的解满足：

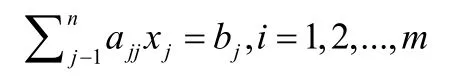
将矩阵A作标准分解可得到：A=D+L+U

其中，D=diag(a11,a22,...,amm)

此时可将式（1）变为：

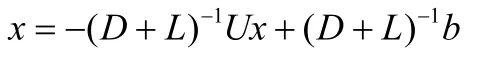
此时，应用雅克比迭代法可以得到：

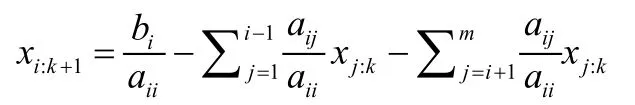
当应用高斯-赛德尔迭代法可得：

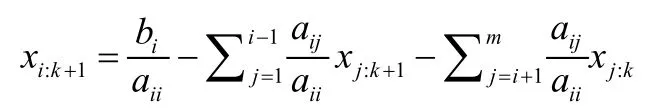
式中 ：i=1,...,m；k=1,2,...

计算xi与k-1次迭代值的加权平均ω作为第k次的迭代值，即：

上式也可整理成：

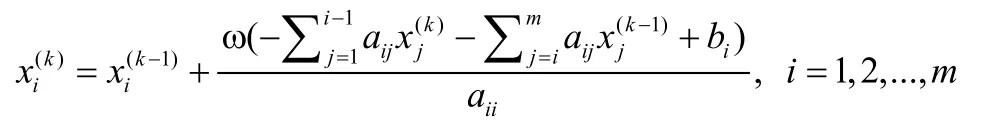
其中ω称为松弛因子，要求0＜ω＜2。当ω＞1时，上式称为逐次超松弛迭代法；当ω=1时，上式即为高斯-赛德尔迭代法；当0＜ω＜1时，上式称为低松弛迭代法[2]。

2 应用案例

如图1所示的电路图中，已知Ue1=8 V,Ue2=4 V,Ue3=2 V,R1=R2=R4=1 Ω,R3=3 Ω,R5=2 Ω,R6=7Ω，利用迭代法求解Il1Il2Il3。

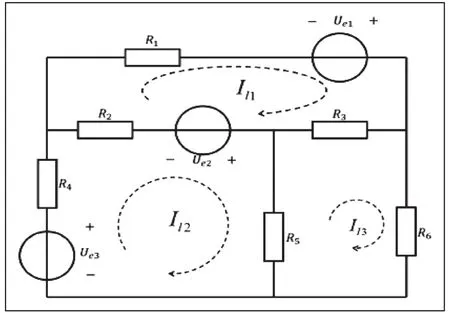
图1 电路图

本文将针对该应用案例使用MATLAB软件实现雅克比迭代法、高斯-赛德尔迭代法和逐次超松弛迭代法在求解线性电路方程中的应用[3]，并对运行结果进行分析。（计算精度控制在10-5）

根据电路等效分析可得：

根据戴维南定理可得：

代入数值：

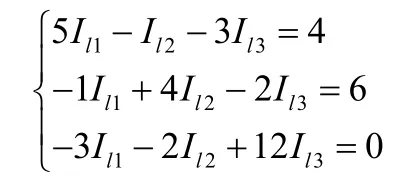
上述方程组对应于（1）式中的A、b矩阵：

3 迭代法的MATLAB实现

3.1 雅克比迭代法的MATLAB实现

Step1：编写雅克比迭代法的程序

Step2：编写验证程序

Step3：运行验证程序jacobi.m，得到在10-5精度范围内的Il1Il2Il3值和计算机迭代次数如表1所示。

表 1

3.2 高斯-赛德尔迭代法的MATLAB实现

Step1：编写高斯-赛德尔迭代法的程序[4]

Step2：编写验证程序

Step3：运行验证程序gauss.m，得到在10-5精度范围内的Il1Il2Il3值和计算机迭代次数如表2所示。

表2

3.3 逐次超松弛迭代法的MATLAB实现

Step1：编写逐次超松弛迭代法的程序

Step2：编写验证程序

Step3：运行验证程序sor.m，得到在10-5精度范围内的Il1Il2Il3值和计算机迭代次数如表3所示。

表3

说明：这里的最佳松弛因子w为1.15，可以通过w取不同值进行验证。

4 总结

由表1-表3可以看出三种迭代法解线性方程组的收敛速度，三种迭代法达到要求的精度（例题要求精度：10-5）所需的迭代次数如下表所示：

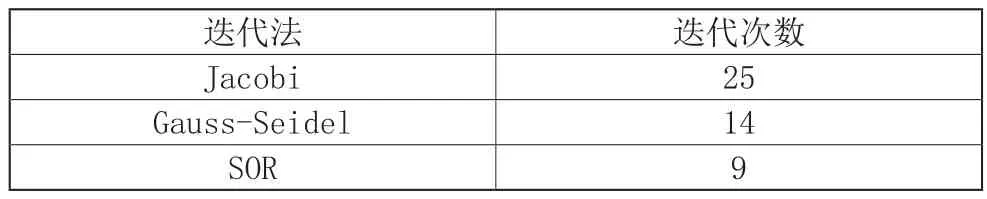
表4

分析表4可以得到逐次超松弛迭代法的收敛速度最快，高斯-赛德尔迭代法次之，雅克比迭代法最慢，通过上面的应用案例可以知道，高斯-赛德尔迭代法可看作是雅克比迭代法的一种改进，逐次超松弛迭代法是高斯-赛德尔迭代法的一种修正。鉴于程序的可移植性，在求解更为复杂的电路时只需要修改程序里的数据参数即可，电路越复杂越能体现计算机的高效。

本文使用了MATLAB软件使电路分析的计算过程得到了极大的简化，同时也为广大学生提供了一种新的解题思路，通过计算机高效的特点，激发学生利用编程软件学习专业知识的兴趣，具有一定的参考价值。