高效连铸相关工艺模型及智能控制系统研发
2021-06-28杨昌霖
杨昌霖
(中国重型机械研究院股份公司,陕西 西安 710032)
0 前言
目前,我国钢铁行业正处于制造大国向制造强国转变的关键时期。连续铸钢作为炼钢和轧钢的中间环节,对产品质量的提升及生产流程的整体优化有重要影响[1]。
随着《中国制造 2025》的提出,产业结构升级调整的步伐正逐步加快,以电炉-精炼-连铸为代表的短流程炼钢技术可能将成为未来的发展趋势[2]。在网络化和信息化技术的推动下,钢铁企业对铸机拉速,铸坯质量及智能化水平提出了更高的要求。
智能化的核心是数据的分析与运用,关键是数学模型的适应性和可靠性。智能化控制系统的建立一方面是通过丰富的数学模型对采集到的数据进行分析处理,得到关于连铸设备和铸坯质量的信息,并在此基础上对工艺参数进行优化[3]。另一方面是在各个模型和模块之间建立一套有效的数据交换机制,实现数据的快速传输和实时反馈,以实现系统的自学习和自适应[4]。围绕高效连铸技术,对现有的工艺模型进行改进升级,开发一个集设计优化模拟于一体的智能控制系统对提升连铸机的工艺技术及装备水平至关重要。
国内外关于连铸智能化的研发主要是连铸动态二冷控制系统的研究与应用。基于人工智能技术的动态配水模型可以解决铸坯表面温度波动大的问题,但系统建模困难,模型的准确性受限于模型的训练次数。为了增强模型的适应性,本系统中的动态二冷水控制模型从传热原理入手,找到水量与板坯表面温度之间的近似关系,采用解析法直接计算二次冷却水量,提高了控制效率和控制精度。
本文首先对连铸智能控制系统的总体框架及功能进行了阐述,然后针对现有技术提出了新的工艺模型,包括结晶器铜板温度场计算,保护渣状态模拟,动态二冷水控制和铸坯三维温度场计算,在此基础上提出了实现数据可视化的思路。钢种物性参数数据库,工艺模型和数据可视化共同构成高效连铸智能控制系统。目前,模型的计算结果已经用于生产过程中工艺参数的确定及设备结构的优化。数据可视化功能无需外部接口和辅助软件,通过创建MFC应用程序,采用windows系统中的图形设备接口GDI可以将模型计算的结果转化为位图数据,从而清晰的呈现出整个连铸过程中各个参数的变化,同时也为用户和技术人员提供设备的实时状态和质量信息。
1 系统总体框架
系统总体框架如图1所示。连铸智能控制系统分为三层,从上到下分别是数据输入层,数据处理层和数据输出层。数据输入层包含建立数学模型所需的所有数据,包括钢种的物性参数、连铸机的几何尺寸和工艺参数。其中,钢种的物性参数利用商业软件JMatPro建立数据库,工艺参数可以人为设定,也可以基于离线模拟的结果进行优化。连铸机的几何尺寸在总体设计模块中进行设定,包括铸机的辊列设计,结晶器内腔形状设计,以及结晶器水缝设计。
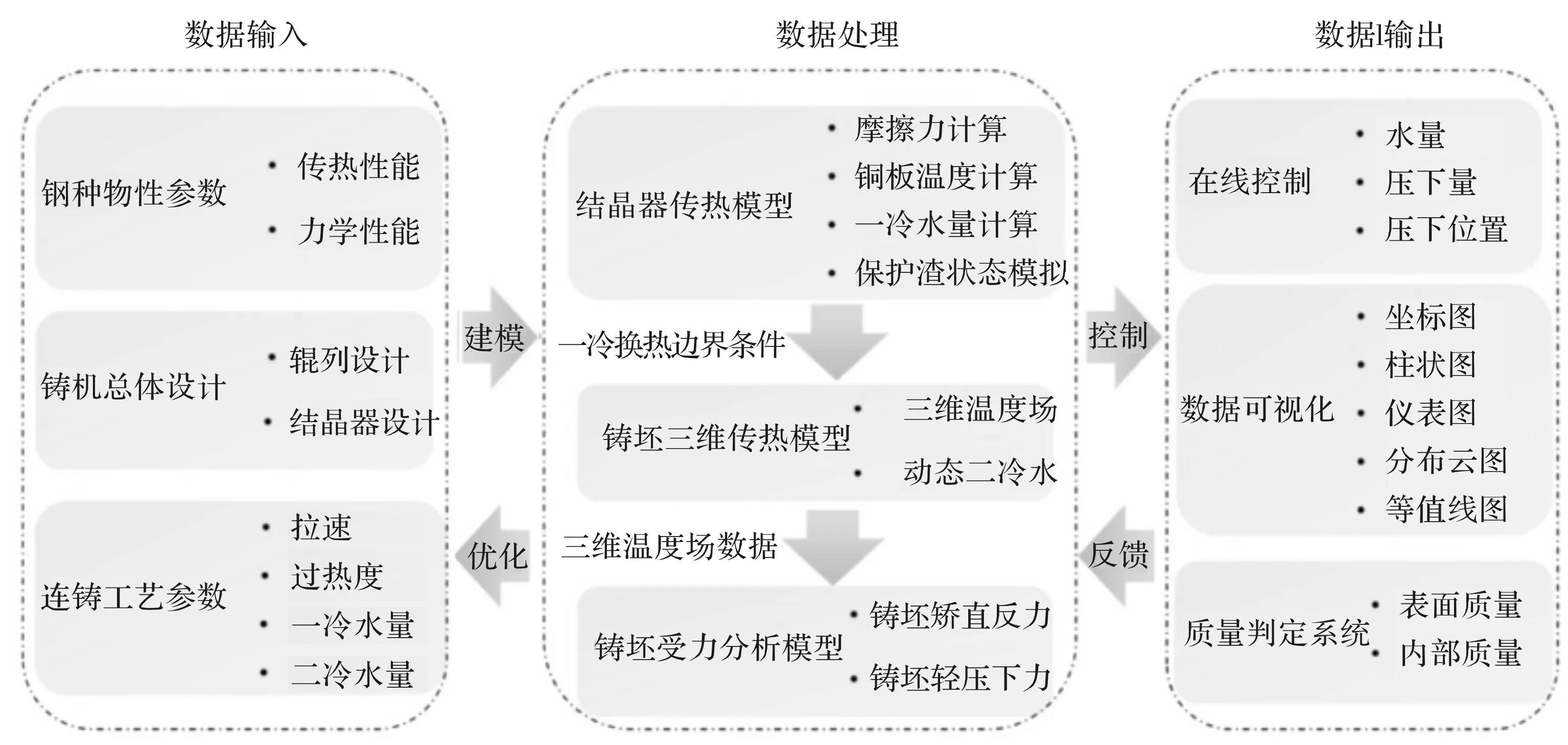
图1 高效连铸智能控制系统总体框架
输入到系统中的数据通过各个数学模型进行分析和处理,得到关于铸坯当前状态的关键信息,并将服务于连铸机的在线控制和铸坯质量的判定。模型得到的数据既可用于连铸机的在线控制,也能用于数据可视化以及铸坯质量的判定。根据质量判定系统反馈的信息决定是否需要对现行的工艺参数进行调整和优化。随着现场经验的不断积累,将会建立一套针对不同钢种在不同浇注条件下的工艺参数数据库,实现生产过程的精细化及智能化。
2 工艺模型
2.1 结晶器内铸坯换热系数计算
连铸过程中,钢液的初始凝固在结晶器内完成[5]。铸坯的热量以传导和辐射的方式通过保护渣到达铜板表面,最终被结晶器水缝内的冷却水带走。结晶器的四块铜板以及保护渣共同构成结晶器内钢液的换热边界[6,7]。铸坯与铜板之间的换热系数是计算结晶器铜板温度、铸坯表面温度以及一冷水量的关键参数。为了得到结晶器内的换热边界条件,以型腔中心为坐标原点建立数学模型,如图2所示,冷却水与铸坯之间的温度分布示意图如图3所示。
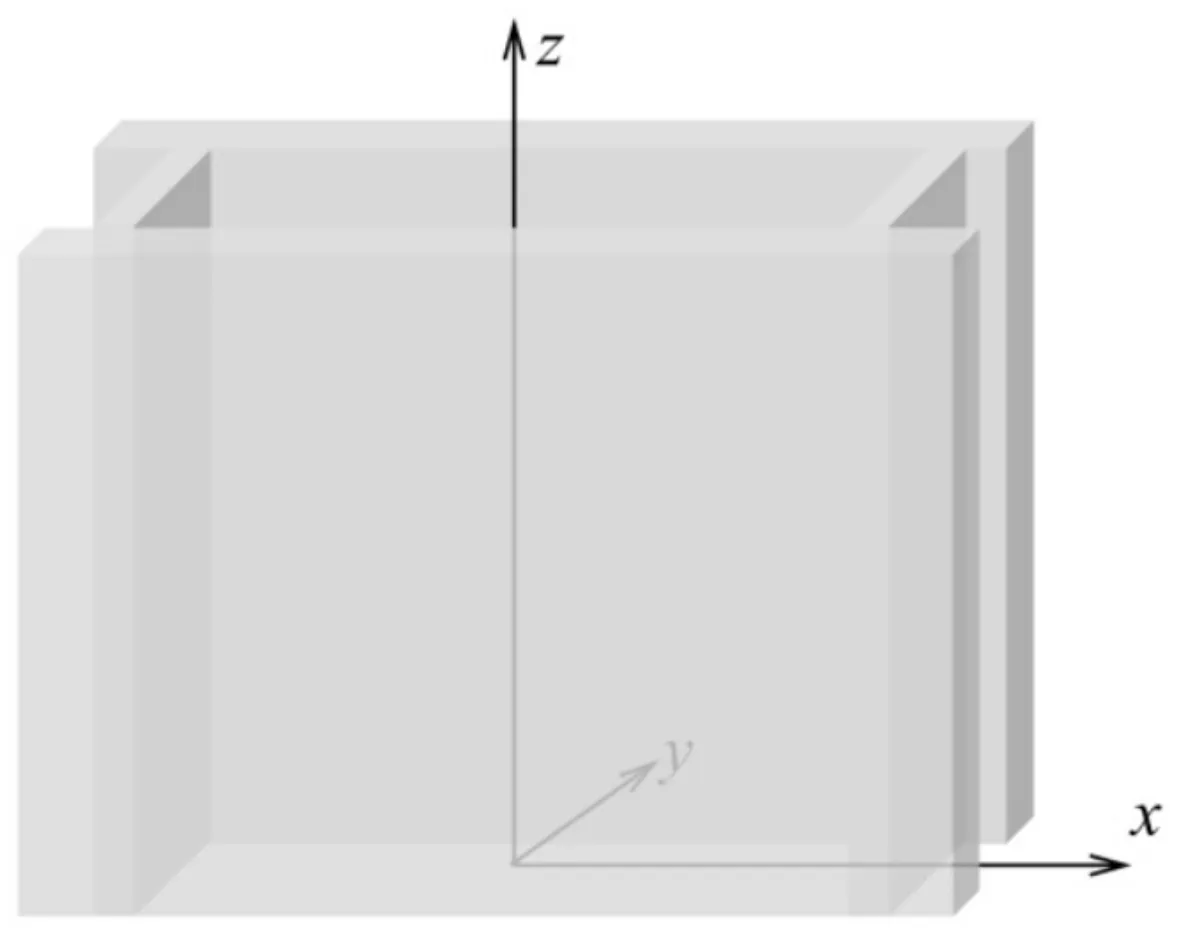
图2 结晶器传热模型坐标系的建立

图3 钢液与冷却水之间的温度分布示意图
根据傅里叶导热定律,通过铜板的热流密度可以表示为
(1)
式中,qz为距液面某个位置到达铜板的热流密度,W/m2;Tsol为钢液固相线温度,℃;Tw为冷却水温,℃;sz为距液面某一位置的坯壳厚度,m;dcu为铜板的有效厚度,m;λs和λcu分别为钢液和铜板的导热系数,W/(m·℃);hf和hw分别为铸坯与铜板之间以及铜板与冷却水之间的换热系数,W/(m2·℃)。
根据钢液凝固的平方根定律
(2)
式中,Vpz为z平面以下的型腔体积,m3;Vp为液面以下的型腔体积,m3;s0是出结晶器的坯壳厚度,m。
联立式(1)和式(2),热流密度在整个铜板上进行积分得到单位时间通过单块铜板的热量
(3)
式中,Qc为单位时间通过单块铜板的热量,W;Af为铜板的有效换热面积,m2。
钢液释放的热量包括三个部分,过热,显热和潜热。
Qf=u0l0[s0ρscpsΔTs+ρsΔHs+s0ρscps(Ts-Tr)]
(4)
式中,Qf为单位时间钢液释放的热量,W;u0为拉速,m/s;ρs为钢液密度,kg/m3;cps为钢液的比热容,J/(kg·℃);ΔTs为钢液过热度,℃;l0为铜板宽度,m;Tr为铸坯表面温度,℃;Ts为钢液固相线温度,℃。
冷却水带走的热量可以表示为
Qw=fwcpwρwΔTw
(5)
式中,Qw为单位时间冷却水带走的热量,W;fw为冷却水的体积流量,m3/s;cpw为冷却水的比热容,J/(kg·℃);ρw为冷却水的密度,kg/m3;ΔTw为冷却水的进出水温差,℃。
根据能量守恒,钢液释放的热量等于冷却水带走的热量,也等于通过保护渣到达铜板表面的热量[8,9]。据此,联立式(3)、式(4)及式(5)可以得到换热系数hf,出结晶器坯壳厚度以及冷却水温差三者之间的关系。铸坯宽度1 600 mm,结晶器有效高度800 mm,出结晶器坯壳厚度15 mm,冷却水温差7 ℃的条件下,不同拉速对应的宽面铜板单侧水量和换热系数的计算结果如图4所示。

图4 不同拉速下水量和换热系数的计算结果
2.2 结晶器内钢液凝固传热计算
根据结晶器与铸坯之间的换热系数可以计算出铜板的温度和铸坯的温度。以结晶器内铜板和铸坯为研究对象,划分单元格如图5所示。

图5 结晶器传热模型单元格划分
与O位置相邻的两个单元格的热流密度可以表示为
qc=hc(Tc-To)
(6)
式中,qc为相邻两个单元格之间的热流密度,W/m2;Tc为与O位置相邻的W、S、E、N四个方向中任意一个方向的温度,℃;相邻两个单元格为不同介质的hc的表达式见表1。

表1 相邻两个单元格不同介质的换热系数的表达式
表1中,lc为相邻两个单元格相互接触的长度,m;d为相邻两个单元格中心之间的距离,m;对于O位置的单元格,四个方向上Tc、lc和d见表2。

表2 O位置不同方向上Tc、lc和d的表达式
表2中,TE、TW、TN、TS分别表示W、O、E、S位置处的温度,℃;Δx和Δy分别为x方向和y方向的空间步长,m;Δz为沿拉坯方向选取的步长,m。对O位置处的单元格可以写出能量守恒方程
(7)

根据式(7),用上一时刻温度可以计算任意位置当前时刻温度。
根据结晶器铜板温度的计算结果可以对铜板内水缝的布置进行优化。对国内某钢厂结晶器铜板的水缝布置进行优化后发现,螺栓两侧水缝的深度与螺栓旋入深度的比值控制在1.10~1.22范围内时,可以最大程度的降低铜板热面温度同时改善传热的均匀性,如图6和图7分别为优化前后铜板断面的温度分布图。

图6 优化前铜板断面温度分布

图7 优化后铜板断面温度分布
2.3 结晶器保护渣状态及摩擦力计算
结晶器与铸坯之间的保护渣能起到润滑铸坯的作用[10]。为了将铸坯与铜板之间的摩擦力定量化,需要明确不同位置保护渣的状态[11,12]。铜板与铸坯之间保护渣的温度分布如图8所示。根据不同位置处保护渣的温度和厚度可以对保护渣进行受力分析,从而计算出铸坯所受的摩擦力。铸坯与铜板之间单元格的划分如图9所示。

图8 铜板与铸坯之间保护渣的温度分布

图9 铜板与铸坯之间保护渣的受力分析
根据本文中给出的换热边界可以确定液态保护渣,固态保护渣和气隙层的厚度
(8)
(9)
(10)
式中,dliq、dsol和dair分别为液态保护渣、固态保护渣和气隙层的厚度,m;λliq、λsol和λair分别为液态保护渣、固态保护渣和空气的导热系数,W/(m·℃);Tfl为保护渣的凝固温度,℃;Tfs为固态保护渣的表面温度,℃;Tcu为铜板表面温度,℃。需要注意的是保护渣的凝固温度随温度和冷却速度的变化而变化,具体数值可根据Hoffman-Lauritzen提出的晶体长大理论进行计算[13]。液态保护渣,固态保护渣与气隙层厚度之和为一定值[14],通常假设为2 mm。
铸坯与铜板之间任意一层的保护渣均受到重力和剪切力的作用,在拉速稳定的情况下合力为零
Fqi-1+ρfgdy-Fqi=0
(11)
式中,Fqi和Fqi-1分别表示第i层和第i-1层保护渣受到的剪切力,N;ρf为保护渣的密度,kg/m3;g为重力加速度,m/s2;dy为每一层保护渣的厚度,m。
保护渣所受的剪切力根据粘度和速度梯度计算
(12)
式中,ηi-1为第i-1层保护渣的粘度,Pa·s;vi-1和vi分别为第i-1层和第i层保护渣的运动速度,m/s。
保护渣的粘度与温度的关系为
(13)
式中,η0为指前因子,Ea为粘流活化能,kJ/mol;R为气体常数,J/(mol·K);T为温度,K。
根据两种保护渣物性参数计算得到的一个振动周期内结晶器内的摩擦力如图10a所示,1 m/min拉速条件下宽面铜板摩擦力的分布如图10b所示,液渣膜厚度分布如图10c所示,宽面铜板热流密度分布如图10d所示。
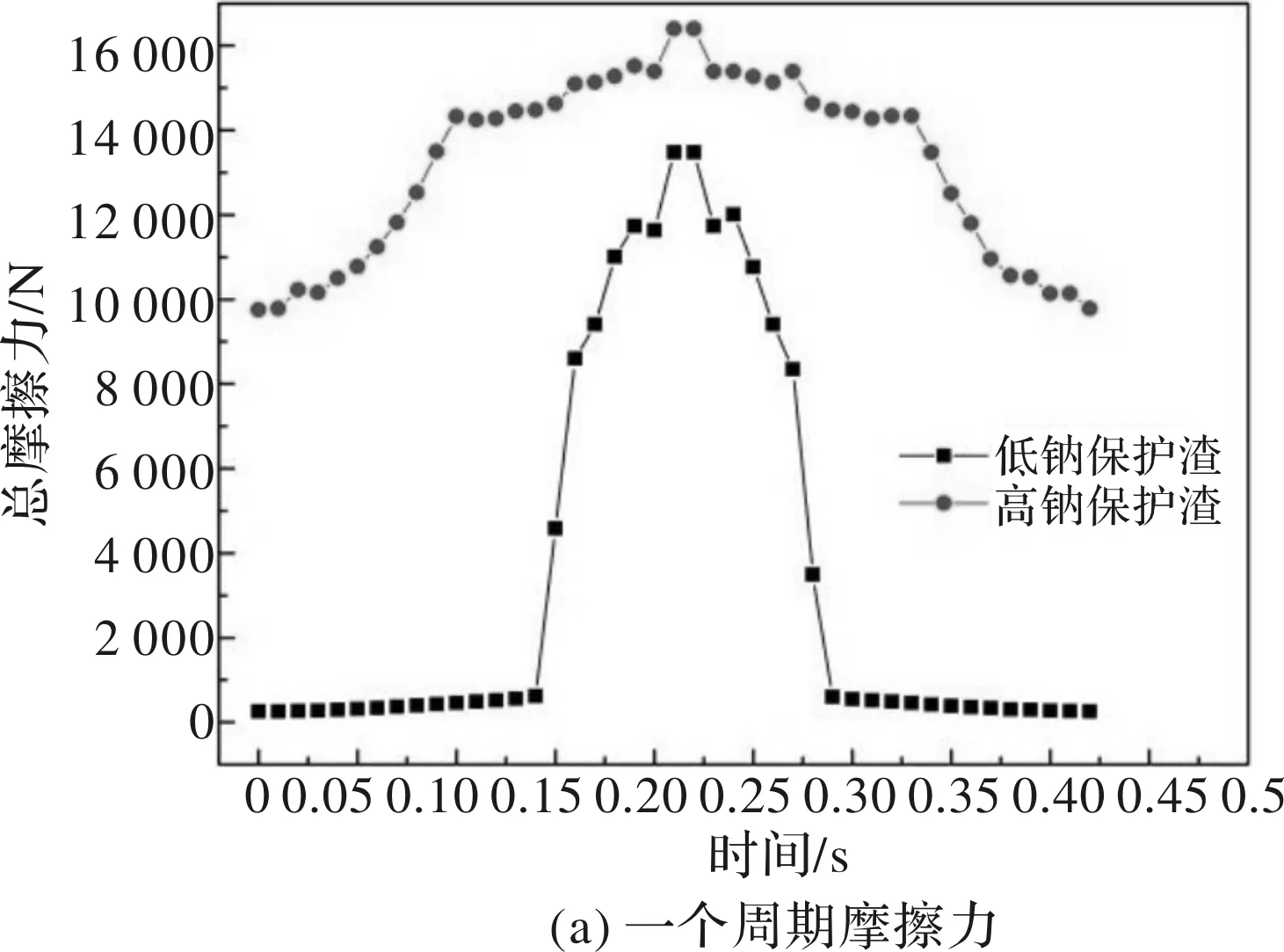

图10 结晶器保护渣状态及摩擦力计算结果
2.4 铸坯三维传热计算
铸坯的三维传热计算将基于有限元的思路,采用坯尾回溯法计算铸坯的温度场。将铸坯从液面至坯尾划分为k层,相邻两层之间的距离为拉坯方向的空间步长Δz,且空间步长,时间步长和拉速之间相互独立。以最后一层为当前层,根据给定的时间步长和拉速计算出Δt时间后到达当前位置的p层,然后根据p层,p-1层,p+1层的温度计算Δt时间后p位置的温度。最后将计算好的温度填入k层完成一个周期的运算。k层的温度填充好后,以同样的方式填充k-1层的温度直至整个铸坯的温度场更新完毕。由此得到一个时间步长Δt内铸坯温度的变化。计算过程如图11所示。

图11 坯尾回溯法计算铸坯三维传热的过程
铸坯内某个点的温度根据能量守恒可以表示为
(14)
Fo=1-2Fox-2Foy-2Foz
(15)
(16)
(17)
(18)

由于空间步长和时间步长与拉速无关,因此模型稳定性好,且计算过程中不需要额外的内存空间,计算效率也较高。
2.5 动态二冷水控制模型
浇注过程中拉速,过热度,钢种发生变化时,铸坯的表面温度会随之发生变化[16,17]。为了保证铸坯表面温度与设定的目标温度一致,需要根据外部条件的变化对各个冷却区的水量进行实时调节[18,19]。
模型假设铸坯宽面中心为一维传热,且铸坯固相内沿y方向的温度分布可以用二次函数拟合,用待定系数法可以得到铸坯宽面中心温度随时间的变化
(19)
式中,θ为Δt时间后铸坯表面温度与环境温度的差值,℃;θ0为铸坯表面的初始温度与环境温度的差值,℃;Δt为铸坯达到目标温度所需时间,可以设定为铸坯经过一个辊距所需时间,s;A和B与钢种物性参数和二冷区边界换热系数有关
(20)
(21)
式中,ht为二冷区域的换热系数,W/(m2·℃);sz为坯壳厚度,m。
根据表面设定温度和浇注条件可以从式(19)中求解出表面换热系数。利用温度与换热系数的表达式可以得到温度变化量与水量变化量之间的关系[20-22],由此可以根据当前温度与目标温度之间的差值计算出目标水量与当前水量的差值。
(22)
式中,ΔQs为当前时刻应该增减的水量,L/min。Δθ为当前温度与目标温度的差值,℃;q′(ht)为温度对换热系数的一阶导数,根据式(19)计算,ht′(Vs)为换热系数对水量密度的一阶导数;Vs′(Qs)为水量密度对水量的一阶导数,其中换热系数与水量密度的关系根据实验确定,水量密度与水量的关系为
(23)
式中,Qs为某个冷却区的冷却水量,L/min;Vs为某个冷却区的平均水量密度,L/(min·m2);Ds为喷水厚度,m;W为喷淋宽度, m;ni、nj分别为某个冷却区起始辊号和结束辊号。
为了提高调节效率,尽量避免超调,模型采用阶段性逐渐调节的策略。根据浇注条件计算铸坯的温度场,每一轮计算完毕后对铸坯温度和目标温度进行比较,当计算温度与目标温度的差值超过临界值时,考虑两种情况:第一种情况是铸坯表面温度逐渐远离目标温度(可根据温度随时间的二阶导数判定),这种情况根据设定的调节频率对水量进行调节;第二种情况是铸坯表面温度逐渐靠近目标温度,这种情况需要先计算Δθ随时间的变化量,当Δθ的变化量小于临界值时,对水量进行调整,可以最大程度避免超调现象。按照这一方法可以保证整个调节过程中,铸坯表面温度与目标温度的差值在±20℃以内(与拉速变化量和铸坯所在位置有关),水量调整结束时,铸坯表面温度与目标温度的差值可以控制在±1℃以内。
3 数据可视化分析
采用windows系统中的图形设备接口(GDI, Graphics Device Interface)实现数据可视化功能。封装在GDI中的CDC类提供了大量的绘图函数。利用这些函数完成铸坯结晶器铜板和其他设备的三维轮廓绘制。然后根据数学模型算出的数据得到每个位置对应的温度或其他物理量的数值,最后根据数值的大小对三维轮廓的内部区域填充颜色,实现温度分布云图和等值线图的绘制。
一个区域内的任意一点的数值都对应一种颜色,每种颜色都对应一个颜色值。在RGB模式下,如果让这块区域的颜色按照数值大小从红,黄,绿,蓝过渡,那么这个颜色值在0~1020之间。每种颜色由三基色,即红(R)、绿(G)、蓝(B)唯一确定。颜色值可以根据某一块区域的最大值和最小值计算:
(24)
式中,colour表示表示某个数值对应的颜色值,为一整数;v表示某个位置对应的数值;vmin、vmax表示某个区域数值的最小值和最大值;layer表示划分的层数;[ ]表示取整。不同颜色值对应的R、G、B的数值见表3。

表3 不同颜色值对应的R、G、B的值
结晶器铜板和铸坯的三维温度场如图12a和图12b所示。从图12a中可以看出,结晶器铜板表面上部的颜色明显比下部的颜色深,说明连铸过程中结晶器铜板从上到下温度是逐渐降低的。类似的可以从图12b中看出,铸坯顶面及铸坯心部的颜色明显比铸坯表面的颜色浅,说明浇注过程中铸坯从外到内逐渐凝固,且中心温度高于表面温度。

图12 结晶器铜板三维温度场和等值线
与分布云图不同,等值线图通过线条反映区域内数值的大小。等值线上各点的数值是相同的。结晶器铜板和铸坯的等温线图如图13a和图13b所示。对结晶器铜板而言,等温线可以反映铜板表面温度分布的均匀性,等温线上下波动越明显,表明铜板表面温度分布不均匀。对铸坯而言,等温线主要反映液相穴的深度和凝固末端的位置。结合分布云图和等温线图可以直观的判断出各项指标是否在正常范围内,以便对设备及铸坯质量进行实时的监控和维护。

图13 铸坯三维温度场和等值线
4 结束语
智能化是未来钢铁行业未来发展的趋势,对提升企业的技术水平,运营效率和管理能力有着不可替代的作用。本文针对连铸过程,通过建立一系列的数学模型,将抽象的物理过程转化为定量的数学描述,并将各模型统一集成,实现数据共享。为工艺参数的优化及铸坯质量的判定提供理论支持,也为今后数据的可视化及生产过程的智能化打下基础。
