汇流阈值拟合分段及沟谷级别对黄土典型小流域盒维数的影响
2021-06-28甘露晏自红刘晋红罗明良
甘露, 晏自红, 刘晋红, 罗明良
西华师范大学,四川 南充 637002
Mandelbrot发表《英国的海岸线有多长?统计自相似和分数维度》提出分形理论后,分形方法在不同领域内都得到广泛的应用,应用于沟谷形态分析[1-5]、地貌格局差异[6],以及土壤侵蚀响应[7,8]等方面。度量水系结构复杂性常用指标之一就是分形维数[9],朱晓华应用分形理论研究了整个中国水系及其各组成水系的分形结构特征[3]。孟宪萌对不同地貌类型的长江流域进行分形分维计算,通过盒维数判定对应的地貌发育阶段[10]。梁春玲计算祖厉河流域分维值,刻画了流域地貌形态特征[11]。何直立将秦岭地区的22个典型流域利用盒维数法进行分析,探索流域形态特征及水文特征的相关性和空间分异性[12]。前人基于分维研究,划分了流域地貌发育阶段[13]。上述研究从全国[3]、流域[10,11]、区域[12]等不同尺度对河网或水系的形态特征进行了研究。从研究的热点区域来看,主要涉及秦岭山区、长江流域等地。我国黄土高原被誉为全球最具有地学研究价值的地理研究区域之一[14],黄土沟谷承袭下伏基岩,在构造、风力和水力等内外营力共同作用下,经流水等的侵蚀,形成了现在形态差异明显的沟谷[15,16]。黄土沟谷研究方面,前人在黄土沟头[17]、沟谷节点提取及分析[7,18]、沟谷密度及空间分异[19]、河网结构及其自相似性[20]、横剖面形态特征[21]等进行了深入研究,分析了影响黄土沟谷发育的上坡汇水面积阈值及其影响因素[22],探讨了黄土地貌发育阶段[23,24]及沟谷侵蚀-堆积过程[25]。这些研究,丰富和发展了黄土沟谷研究,尤其是数字高程模型(Digital elevation model,DEM)及数字地形分析方法,在地貌形态研究中得到深入应用,启迪了基于DEM的黄土沟谷分维特征研究的新思索,产生了新的疑问:流域的上游一般坡度较大[22,26],与中下游相比形态差异明显;如果采用盒维数D=1.6来划分全流域地貌发育阶段,将无法体现流域源头与其他河段的差异,结论相对勉强[27]。能否分别对河流上游及其他河段进行形态分析,研究其盒维数差异?一级支流盒维数如何区别于其他级别?基于上述考虑,以黄土高原绥德典型小流域为例,分析了不同汇流阈值提取沟谷对盒维数的影响;对比了全流域尺度盒维数与不同河段盒维数的差异;探索了级别差异如何影响盒维数。
1 数据与方法
1.1 实验样区
典型小流域沟位于陕西省绥德县(见图1),在黄土高原丘陵沟壑区第一副区具有代表性。该流域的气候类型为半干旱大陆性气候,区域内水土流失严重,多年平均降雨量为475.1 mm;全年64.4%的降雨集中于七、八、九月的汛期中,多出现暴雨天气。该小流域是无定河中游的一条支沟,流域面积70.7 km2,主沟长18 km,沟壑密度是5.34 km·km-2。
1.2 水系提取的基本步骤

图1 绥德流域 DEMFig.1 DEM of Suide valley
采用1∶1万DEM作为基本数据,基于地表径流漫流模型河网水系提取。水文分析步骤如下:填洼DEM;在ArcGIS平台下通过D8算法来确定水流方向;流量累积栅格的确定;提取水系。设置200和1 800两个阈值对该小流域进行河网的提取。当汇流累积量为1 800 时,所提取的河网密度3.15 km·km-2最接近实际情况。考虑不同阈值对盒维数的影响,选择了阈值差距接近为10倍的200作为对比阈值参数(见图2)。

图2 盒维数流程图Fig.2 Box dimension flow char
1.3 盒维数法
水系的分维一定程度上反映了水系发育程度,常用的分形维数有盒维数,关联维数。本文采用盒维数法来描述小流域的分形特征。基于水系的长度流域面积关系采用网格覆盖法来计算盒维数。即为,采用正方形格网来覆盖研究范围的河网,再求出覆盖整个水系的正方形格网数目。随着格网边长的变化,网格数据也随之改变。用边长和格网数目做双对数,再对其进行线性拟合,拟合出的直线斜率即为所求盒维数。
何隆华、赵宏等人提出了基于盒维数划分流域地貌发育阶段的标准。认为,当流域范围里的水系的分维数小于1.6时,流域地貌处于侵蚀发育阶段的幼年期;当分维值大于1.6小于1.89时,流域地貌属于壮年期;当分维值大于1.89小于2.0时,流域地貌处于侵蚀发育阶段的老年期。
2 结果与分析
基于绥德典型小流域1∶1万的DEM,选取阈值为1 800进行水文分析,构建河网。采用网格法进行分形分维分析计算盒维数,网格长度和网格数目分别求对数,再对其进行线性分析,得到以下关系式,如图3所示:

其中X为网格长度对数,Y为网格数目对数,其线性回归关系式的相关系数R2为0.99,表明网格长度与网格数目密切相关,证明在1 800阈值下河网的分形分维特性是客观存在的。1.23为阈值1 800提取的河网的盒维数(见表1)。

图3 阈值 1 800 网格法计算Fig.3 Threshold 1 800 grid computing
由图3可以看出,尽管得到较好的双对数线性关系,但是图中点对应存在两段线性趋势。分别拟合两段线性关系得到的回归方程如(2)(3)所示。其中(2)对应的无标度区间为[3.66, 2.64],(3)对应的无标度区间为[2.30, 1.17]。
为探究两个无标度区间对应的沟谷位置,将无标度区间对应的栅格像素叠合得到图4所示的空间示意图。从图中可以看出,该无标度区间所对应的位置大致为小流域源头区。另一个无标度区间对应的空间位置大致为小流域的中下游。
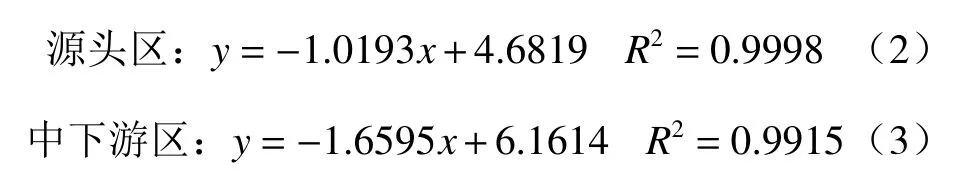
由此可知,尽管盒维数可以用来描述流域地貌形态,但源头区和小流域中下游显著不同。为了印证这一观点,进一步单独提取了小流域一级支流,其盒维数为1.08.表示这部分为沟谷幼年期,代表了沟谷源头区的发育状态。
为了印证这一观点,设定阈值为200,重复以上实验,得出小流域整体盒维数为1.48;分段拟合的盒维数为1.07和1.66。一级支流的盒维数为1.29(见表1)。
3 讨论
(1)阈值对沟谷盒维数的影响
从表1可知,阈值在200时提取的河网在全局、源头区和中下游计算的盒维数分别为1.48,1.07和1.66。阈值为1 800时提取的河网在全局、源头区和中下游计算的盒维数分别为1.23,1.02和1.66。阈值为200和1 800提取的河网在全局和源头区盒维数均小于1.6,表明流域发育阶段均为幼年期;中下游阶段均大于1.6,则流域发育阶段为壮年期。

表1 小流域盒维数值Tab.1 Box dimension of Suide small valley

图4 研究区提取河网Fig.4 Extraction of river network in the study area
阈值为200提取的河网和阈值为1 800提取的河网如图4所示。从图4可以看出,阈值为200提取的河网是包括小沟谷在内的沟谷网络,而阈值为1 800提取的河网是相对较大的沟谷网络。并且如表1所示,阈值为1 800的河网的盒维数均比阈值为200时河网的盒维数小,由于1 800时的沟谷密度为3.15 km·km-2,小于200时的沟谷维数,表明沟谷密度对盒维数影响较大。
(2)河流上中下游对盒维数的影响
小流域进行分段拟合其盒维数,通过表1可以得到,河流的源头区阈值为200和1 800提取的河网盒维数分别为1.07和1.02,为河谷发育的幼年期;河流的中下游盒维数均为1.66,为河谷发育的壮年期。从河流的分段来看,河流源头区的盒维数比中下游盒维数小,河流源头区比中下游发育阶段更年轻。
研究区域的全局及分段的变化会影响沟谷的盒维数,从表1看出,沟头处一般为幼年期,中下游可能是壮年期。实际小流域地貌受流域地区的植被分布情况,地貌类型,地质构造等因素共同作用,全局的单一分维数而言,并不能代表整个小流域的分形特征。
(3)河网等级对沟谷盒维数的影响
阈值为200和1 800提取的河网一级支流全局盒维数分别为1.29和1.08,全流域盒维数分别为1.48和1.23。一级支流全局盒维数均小于全流域盒维数。一级支流源头区和中下游区盒维数也同样小于全流域源头区和中下游区盒维数。表明,一级支流河网发育阶段比全流域更加年轻。对分级支流来看,本文仅分析一级支流的分维数,对于不同级别的支流之间分形分维特征的变化趋势也值得进一步研究。
