基于AP-CAN的增量关联挖掘算法研究
2021-06-28严加琪
洪 炎,张 磊,严加琪
(安徽理工大学电气与信息工程学院,安徽淮南 232001)
关联规则学习(associate rule learning)是指从一定数据或其他信息载体中挖掘项目及对象之间的相关性,其结果可以揭示数据中隐藏的关联模式。通常关联规则挖掘过程主要包含两个阶段:第一阶段必须从资料集合中找出所有的高频项目组,第二阶段在这些高频项目组中产生关联规则[1]。
1994年Agrawal等提出了Apriori算法[2],采用先连接后剪枝的方法处理选出的候选集来获取频繁项集,该方法需要两次扫描全局事务数据库而生成大量候选集。为了克服Apriori算法的局限性,2000年Han等提出了基于树型的频繁模式增长(FP-Growth)算法[3],将提供频繁项集的数据库压缩到一棵频繁模式树中,占用了更大内存。以上方法均适用于处理静态数据。为处理动态数据的挖掘问题,Leung等提出了基于自然序树CAN-tree结构构建算法[4],该算法克服了FP-tree构建算法占用内存大的不足,但在处理大数据集时的挖掘效率却会降低。
CAN-tree 利用树型存储了所有数据,可以在改变数据量或最小支持度下多次挖掘。Sadat 等[5]在2015年将CAN-tree算法和FP-Growth算法相比,发现在最小支持度较高时,CAN-tree算法的效率更好,但在最小支持度较低时,CAN-tree算法效率低于FP-Growth算法。2008年邹力鹍等[6]提出用子父节点指针替代原父子节点指针,可快速生成条件模式树。2014年陈刚等[7]提出一种基于CAN-tree的快速构造算法,通过增加基于hash表的辅助存储结构、减少项目的查找时间来提高算法效率。Roul等[8]在2014年提出了生成和归并树。但是以上方法均未改变CAN-tree存储规模,导致不同数据量对算法的效率影响过大。为减少CAN-tree规模,在提高挖掘效率的同时优化CAN-tree算法的稳定性,本文提出一种基于AP-CAN的增量关联挖掘算法。
1 CAN-tree算法
增量关联规则挖掘领域主要包括Apriori增量挖掘算法、FP-tree频繁模式增长算法和基于自然序树的CAN-tree算法。CAN-tree采用前缀树的结构,在构建时相同项目共用一个节点,将事务集中,每个项目按序依次插入CAN-tree中,随之生成有序的CAN-tree,在进行增量关联规则挖掘时,更新的事务排序可直接插入构建好的CAN-tree中。相较其他算法,CAN-tree算法的优势在于动态数据的挖掘,只需扫描一次事务集即可构建CAN-tree,提高了增量关联规则挖掘效率。
CAN-tree算法采用先建树后挖掘的方法找出事务中的频繁项集,建树过程:
(1)按特定的序列(一般包括字典序、字母序等)为树设计一个项目头表;
(2)创建一个树的根节点root;
(3)全局扫描数据库,将每一条事务的项目依照项目头表进行排序,对排序后每个项目x进行树的节点插入操作;
(4)遍历与x同名节点路径,若其对应已建立的同名节点的父节点与执行插入事务中项x的前项名相同,则将与x项同名节点的计数增加1,否则创建一个新节点N1,新节点N1的父节点与插入事务中x项的前项名相同,按此方式直到所有项全部插入。
CAN-tree挖掘频繁项集过程:
(1)从CAN树节点自下而上挖掘,先找最下面的项,构建每个项的条件模式基(CPB),再顺着CAN树,找出所有包含该项的前缀路径,即该项的条件模式基;
(2)累加每个CPB上的项的频繁度计数,过滤低于最小支持度的项,构建条件FP-tree;
(3)递归挖掘每个条件FP-tree,累加后缀频繁项集,直到条件FP-tree为空或者条件FP-tree只有一条路径。
CAN-tree中存储了事务集中的全部数据,当事务集条数或支持度改变时,建树无需扫描原事务集,但大量存储的数据使构建CAN-tree的规模过大,占用系统内存。
2 AP-CAN快速构建算法
当CAN-tree 算法的树规模过大时,挖掘频繁项集的效率明显下降,在处理多事务数据库时,为提高挖掘效率需降低CAN 树规模。表1 第2 列为更新前事务集表,其中每条事务的项目均已按字母序排序,构建的CAN树如图1所示。从图1可以看出,按字母序排序后的树中的节点分散,在最小支持度已知条件下包含事务集中所有项,导致树的规模过大。如果在构建CAN 树前就筛选出不满足最小支持度的项,让相同的项共用一个树节点,则可有效减小CAN 树规模,减少挖掘频繁项的时间。基于此,本研究提出一种先聚类后按数据量排序的AP-CAN 算法,即首先按项目的最小支持度删除低于最小支持度的项,然后将剩余项按其支持度计数大小对每条事务重新降序排列,此方法可大大减少节点个数,削减CAN树规模。按支持度重新排序后的事务集如表1第3列所示,构建的AP-CAN树如图2所示。
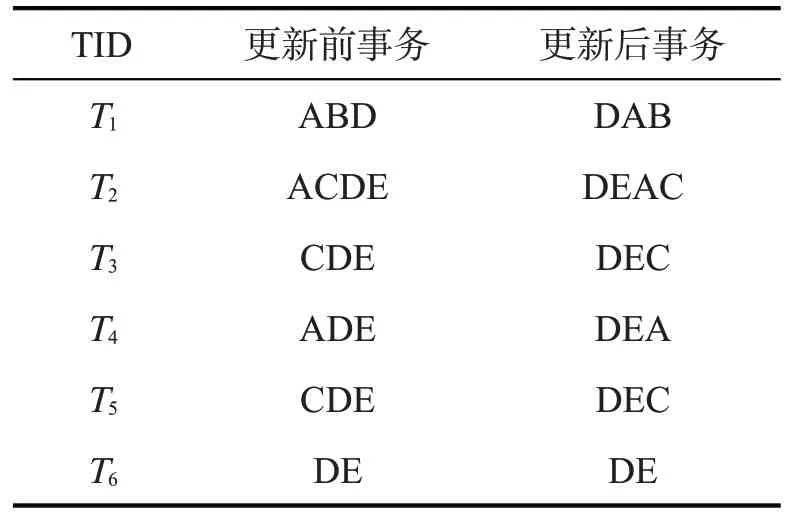
表1 更新前后事务集表
从图2 可以看出AP-CAN 树规模较小,树中仅有7 个节点,先聚类后按数据量排序的方式较传统的排序方式所得到的树规模显著减小。

图2 AP-CAN树
改进后的AP-CAN树和传统FP树不同,有以下优点:
(1)改进后的AP-CAN 树只需对数据库进行一次扫描即可构造树,而FP树则需要对数据库进行两次扫描,节省了扫描数据库所需的时间,提高后续挖掘的效率;
(2)在挖掘动态数据库时,改进后的AP-CAN树可在原有树中进行修改,不受项目增减的影响,而FP树每次改变数据库时都需重新建树。
3 基于AP聚类算法裁剪数据库
在对数据库的每条事务排序前,首先基于数据库中每个项目的支持度进行AP聚类,将原始数据库划分为两个集群(如图3所示),用python随机生成含100个项目的事务集,在一定的最小支持度下通过AP聚类算法分为不满足最小支持度的项目集C1和满足最小支持度的项目集C2。然后,从数据库中删除不满足最小支持度的集群C1,削减了原事务集的项目条数,根据聚类后的集群可以获取事务集的频繁项目及其支持度。AP聚类后不仅会在建立基于哈希结构的项头表时免除扫描数据库,也可以直接将低于最小支持度的项舍去,这样在构建CAN-tree前就可以通过减小树的规模来提高算法效率。

图3 基于项目支持度的聚类结果
3.1 增量更新排序数据库
对于满足最小支持度的项目集群按其支持度排序更新数据库,将每条事务中支持度大的项目放在前面,支持度小的项目放在后面,对经过排序后的数据库构建CAN树时让原本分散的节点在具有相同数据项时共用节点,所构建的CAN树规模大大减小。
3.2 增加基于哈希树结构的项头表
一般在构建CAN-tree 结构树之前,需要设计一个包含所有项目的项头表,将事务集中每条事务按项头表进行排序。本文把按顺序查找的项头表替换为哈希表的数据结构,其查找性能比顺序查找性能好。在含n个项的集合中查找某一项,按顺序查找的时间复杂度为O(n),而按哈希表查找的时间复杂度为O(1)。由于在构建CAN-tree 时频繁地访问项头表会花费大量时间,而改进后的哈希项头表实现了项目的快速查找,在挖掘频繁项时大大提高了算法效率。
3.3 改进CAN-tree结构
构建新型的CAN-tree,首先对数据库进行预处理,基于每个项目的支持度计数对数据库进行AP聚类划分集群,从数据库中删除不频繁的项目,根据聚类后的集群获取频繁项目及其支持计数,记录频繁项目并更新数据库。然后,构建一个项头表(基于哈希结构的辅助存储表),按项目支持度对更新后数据库中每条事务进行增量排序,对每个项目进行树的节点插入操作。具体实现流程如图4所示。
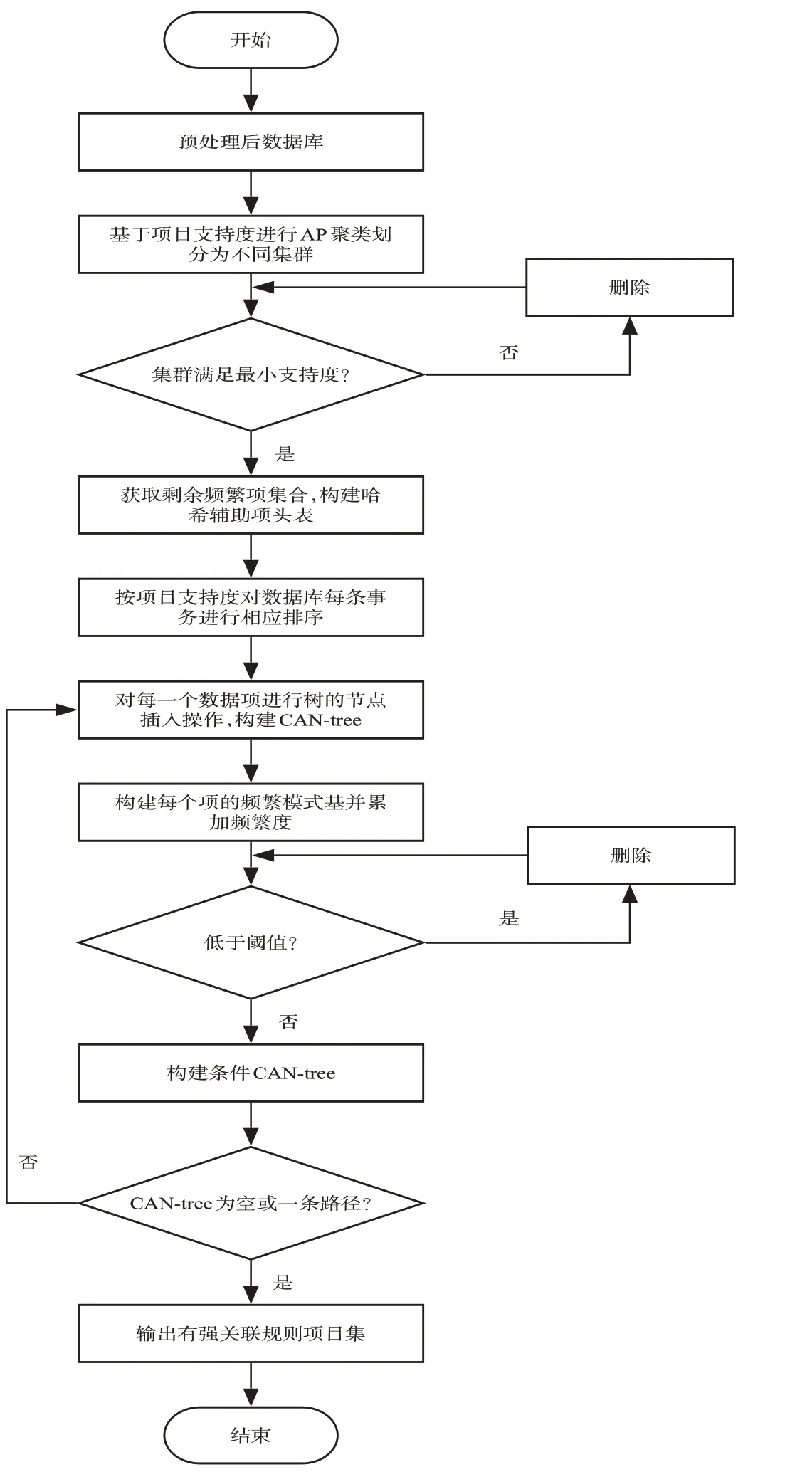
图4 AP-CAN算法实现流程图
4 实验结果分析
实验环境为Intel core i7-9750CPU,8GB内存,window10 操作系统,所有算法均使用python3.7编程实现。实验使用了T10I4D100K和movieItem 两个公开数据集,T10I4D100K数据集具有事务条数多的特点,movieItem 数据集中单个事务数据比较长,大量单个条目达500 项。实验采用3 种挖掘算法来进行对比实验。
4.1 基于模式树构建时间对比实验
将T10I4D100K 数据集分别导入APCAN、CAN-tree、FP-growth这3种不同的算法中,在最小支持度为0.1的条件下,3种算法建树所需时间如图5 所示。从图5 的测试结果可以看出,FP-growth 算法在建树时由于要对项头表进行大量排序工作,时间效率最低;AP-CAN算法由于削减了数据集规模,故建树时间相较于传统CAN-tree算法效率更高。

图5 T10I4D100K数据集下3种算法的建树时间对比
4.2 基于T10I4D100K数据集对比实验
将T10I4D100K数据集分别导入AP-CAN、CAN-tree、FP-growth这3种不同的算法中,在最小支持度为0.3的条件下,挖掘时间结果如图6所示。

图6 T10I4D100K数据集下3种算法的挖掘时间。(a)AP-CAN算法;(b)CAN-tree算法;(c)FP-growth算法
从图6 可以看出,在同一支持度和数据量的条件下,AP-CAN 算法的挖掘时间约为0.47 s,低于CANtree算法且明显优于FP-growth算法的挖掘时间。
为了进一步观察3 种算法的挖掘效率,取最小支持度为0.05,将基础数据量定为40 000,每次使用不同增量进行实验,结果如图7 所示。从图7 可以看出,AP-CAN 算法的数据挖掘时间比FP-growth 算法的挖掘时间要少,其原因在于FP-growth 算法及CAN-tree算法所构建的树规模过大,挖掘频繁项时耗费大量时间,而AP-CAN 算法所构建的树经过AP 聚类算法的削减后规模显著减小。从图7还可以看出,当数据量逐渐增大时,树的规模也在变大,AP-CAN 算法的低时间复杂度特性就越明显。

图7 T10I4D100K 数据集下3 种算法的挖掘时间对比
4.3 基于moveItem数据集对比实验
将movieItem 数据集分别导入AP-CAN、CAN-tree、FP-growth 这3 种算法中,在最小支持度为0.1 的条件下,挖掘时间结果如图8所示。

图8 movieItem数据集下3种算法的挖掘时间。(a)AP-CAN算法;(b)CAN-tree算法;(c)FP-growth算法
从图8可以看出,在同一支持度和数据量的条件下,和图6相比,对于movieItem数据集AP-CAN算法的挖掘时间约为3.26 s,大大优于CAN-tree算法的13.30 s和FP-growth算法的27.78 s。
在最小支持度分别为0.02、0.04、0.06、0.08、0.10条件下,3种算法的挖掘时间如图9所示。从图9 来看,FP-growth 算法在数据量增加时,项头表要进行大量排序工作,而CAN-tree 算法中保留了大量非频繁项目,增加了大量新节点,也需花费部分时间。因此,FP-growth 算法和CAN-tree 算法的挖掘时间远远高于AP-CAN算法的,而且随着最小支持度的降低,AP-CAN算法的挖掘效率的提升效果越显著。

图9 movieItem数据集下3种算法的挖掘时间对比
综上分析,基于AP-CAN的增量关联挖掘算法在处理不同类型的数据集时,在误差允许的条件下,基于不同数据量下的挖掘效率和不同支持度下的挖掘效率相近,挖掘效率约为传统的CAN-tree算法的3倍,约为FP-growth关联规则挖掘算法的10倍。
5 结论
综上所述,针对动态数据本文提出了一种基于AP-CAN的增量关联挖掘算法,该算法在引入AP聚类算法的基础上,通过改变数据量排序方式对数据进行优化处理,增加了一个基于哈希函数辅助存储结构对项头表加以改进。在movieItem和T10I4D100K数据集上的实验表明,本文提出的AP-CAN算法可有效减少CAN-tree的规模,提高增量关联规则挖掘效率,在数据挖掘领域有较高的应用价值。
