无信号交叉口的交通自组织行为建模分析
2021-06-28侯雨晴郝庆一
侯雨晴,郝庆一
(安庆师范大学数理学院,安徽安庆 246133)
近年来,随着经济和社会生产力的快速发展,人们的出行方式发生了极大的改变,交通事故频发,交通问题引起了广泛关注。于是,越来越多的交通模型被提出用以研究交通问题,其中元胞自动机(Cellular Automata)模型[1-2],又称CA模型,其规则简单,易于仿真,能再现交通流复杂系统的很多动态特征,被广泛应用到交通流研究领域。1992 年,Nagel和Schreckberg 提出了模拟单行道交通流模型的基本元胞自动机模型[3],简称NS模型。在NS模型的基础上,大多数元胞自动机模型被拓展到用真实的交通因素来研究系统的特性,如交叉口、限速区、收费站、交通信号灯[4-5]等等。
交通信号灯用于平面交叉口,通过对同时到达交叉口的车辆发出指令,减少车辆间的互相干扰,提高道路的通行效率,保证了交叉口的交通安全。但由于经济条件限制,部分地区基础建设有所欠缺,信号控制系统不完善,当两辆车从两个不同的方向接近无信号控制的交叉口时,驾驶员必须对如何通过交叉口做出决定,驾驶员的决定直接影响交叉口的行车安全以及道路的通行效率。所以,如何建立有效的博弈规则、增加道路通行效率[6-8]是我们研究的主要课题。
传统观点认为,车辆密度高时,有信号控制的交叉口的通行效率一定优于无信号控制的自组织行为。然而,在博弈规则的作用下,可能出现自组织行为的通行效率更优。本文将博弈作为理性的决策过程引入无信号平面交叉口的模型中,研究驾驶员决策对道路通行效率的影响。
1 模型描述
本文提出一个包含两条一维垂直封闭链条的元胞自动机模型[9-10],如图1所示。链条代表单向车辆交通流的车道,一条链的交通流向是自南向北,另一条是自西向东。每条链由相同属性的L个元胞组成,每个元胞依次编号i=1,2,3,…,L。两条链交叉于i1=i2=L/2 处,时间离散。每个元胞在每个时刻的状态只能为空或被速度为1的车辆占据,每辆车在每个时刻的速度为0或1,即每时刻仅移动1个元胞。
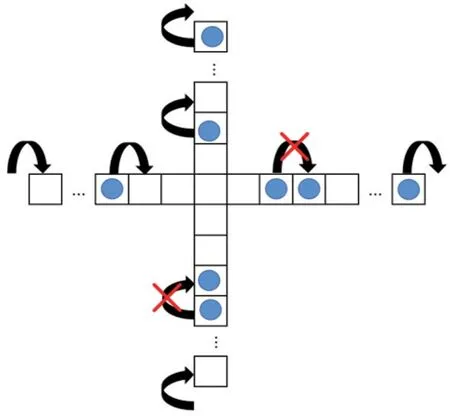
图1 模型示意图
更新规则:前方邻居为空时,下一时刻车辆移动到前方空位;前方邻居被占据时,下一时刻车辆保持不动。采用周期性边界并行更新。
当只有垂直车道的车辆接近无信号控制的交叉口时,驾驶员只需要考虑前方交叉口的车辆情况,当前方交叉口为空,车辆可以顺利进入交叉口。但是,当水平车道同样有车接近交叉口时,驾驶员需要同时考虑前方交叉口及另一条车道的车辆情况。一般认为驾驶员有两种策略选择,合作(C)或背叛(D),持C策略的驾驶员在接近交叉口时大概率选择退让以避免冲突,持D策略的驾驶员则大概率选择直接通过以避免等待。这样就会出现四种博弈情况:(C,C)、(C,D)、(D,C)、(D,D)。如果两条车道上接近交叉口的驾驶员同时采取C策略,此时两车进入交叉口的概率相等,两车的收益都等于1/2;如果两条车道上的驾驶员一个采取C策略,一个采取D策略,此时C策略进入交叉口的概率为(1-r)/2,D策略进入交叉口的概率为(1+r)/2,持C策略的驾驶员收益为(1-r)/2,持D策略的驾驶员收益为(1+r)/2,其中r为参数,调整r的大小可控制不同策略进入交叉口的概率;如果两条车道上接近交叉口的两位驾驶员同时采取D策略,此时极大可能发生冲突,2辆车在2个时间步内均保持不动,且收益都等于0,其余车辆可以正常移动。模型的收益矩阵见表1。
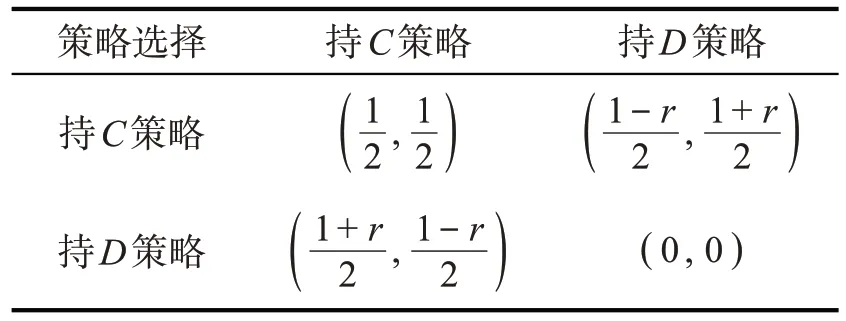
表1 模型的收益矩阵
与“囚徒困境”[11]等经典的博弈模型不同,“赢留输变”[12]是一种相对有效的策略,可以用来应对驾驶员的困境。当双方发生博弈后,成功进入交叉口的车辆,称之为博弈获胜方,反之为博弈失败方。博弈获胜方成功进入交叉口,下一时刻会继续保持此策略,希望下次博弈继续获得胜利。博弈失败方没有成功进入交叉口,只能原地等待,所以下一时刻选择以概率p改变策略,希望获得下次博弈的胜利。当博弈获胜方进入交叉口后,若后方邻居已被车辆占据,则后方邻居内的车辆会选择“贪小便宜”,紧跟前方车辆进入交叉口[6],不再与另一条车道上的博弈失败方博弈。但人的忍耐都是有限度的,当跟随的车辆超过博弈失败方的忍耐限度w,0 ≤w≤6,博弈失败方不会再继续忍耐,而是选择与另一条车道的车辆持续博弈,直到通过交叉口为止。
2 模拟与分析
模拟时,设置系统长度L=1200,N1=N2,其中N1、N2分别表示垂直、水平车道车辆总数,数值结果是在丢弃t0=5×103个初始瞬态后,持续t=15×105个时间步长,经过多次模拟后得到的平均数据。用ρ表示系统的车辆密度,即系统中被车辆占据的元胞数占元胞总数的比例。p表示博弈失败方下一时刻改变策略的概率,w表示博弈失败方的容忍度。用Pc表示系统的合作率,即系统中持C策略的车辆占全体车辆的比例。用F表示车流量,即经过右边界的平均车辆数。F=m/(t-t0),其中t0是系统达到稳态的初始时间,t是系统总的演化的时间,m是t-t0时间步内经过右边界的车辆总数。调整参数ρ、Pc、p、w的大小,观察不同参数下车流量F的变化情况。
现研究r=0.5、Pc=0.5时,博弈失败方下一时刻改变策略的概率p对车流量的影响。图2显示了车流量随车辆密度变化而变化的3个阶段:自由流阶段、相分离阶段和堵塞阶段。(1)ρ<0.2时为自由流阶段,车流量持续增加,p对车流量没有明显影响,两条车道的时空图分别对应图3中的(a1)、(b1),此时系统内的车辆可以自由移动,整体呈均匀分布。(2)0.2 ≤ρ≤0.7时进入相分离阶段,车流量趋于稳定,稳定的高度和长度受概率p的影响,当p充分小时,在ρ≈0.25时出现一阶相变,即流量的突然改变,时空图分别对应图3中的(a2)、(b2),车辆在路口上游拥堵,下游自由流。(3)ρ>0.7时进入堵塞阶段,车流量持续降低,时空图分别对应图3中的(a3)、(b3),车辆整体成拥堵状态。模拟前,猜想越大的p值对应的车流量应该越高,但模拟后的结果是:当p>0.1时,越大的p值车流量越低。

图2 不同概率p下的密度-流量图

图3 p=0.5时不同密度下系统的时空图。(a)垂直车道;(b)水平车道
我们用Pc0表示系统的初始合作率,图4显示了在r=0.5、p=0.5 时,Pc随车辆密度的变化情况。(1)当Pc0<0.5 时,初始系统中选择合作策略的数量少于背叛,人们发现,选择背叛策略不仅不利于个人收益,而且影响整个系统的通行效率,于是越来越多的人选择合作策略希望获得集体收益最大化。(2)当Pc0>0.5 时,初始系统中选择合作策略的数量大于选择背叛策略的数量,大多数人无法实现个人收益最大化,越来越多的人选择背叛策略以保证个人收益。当ρ=0.25时,系统经过多次博弈达到平衡,Pc逐渐稳定在0.5左右。
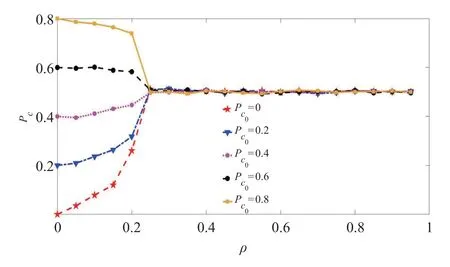
图4 r=0.5、p=0.5时,Pc随车辆密度的变化情况
根据有信号控制的平面交叉口的特点,规定周期T内,交叉口只允许一条车道的车辆通行。取w的值分别为10、20、30、40、50,T的值分别为10、20、30、40、50。观察系统的车流量和平均速度的变化情况。从图5可以观察到自组织行为在高密度下的通行效率明显优于有信号控制的系统,有信号控制的系统在ρ≈0.75时会出现车流量和平均速度的突然改变。Chattaraj[13]也曾做过关于不守规则的印度人与遵守规则的德国人的行人流实验,结果发现在相同密度下印度人的通行效率反而高于德国人,实验结果与本文模拟结果基本一致。

图5 (a)不同w下无信号控制的系统和(b)不同T下有信号控制的系统的车流量和平均速度
3 结论
本文在NS模型的基础上,对无信号控制的平面交叉口的自组织行为进行建模分析,用博弈规则描述车辆通过无信号控制的交叉口的博弈过程,分析了不同参数下系统的车流量、平均速度及相变情况。研究结果表明,参数p和r的大小都会对系统的车流量造成明显的影响,但初始合作率对系统车流量的影响不大,系统最终合作率稳定在0.5左右,博弈规则控制下的自组织行为在无信号控制的交叉口的通行效率比有信号控制的交叉口的通行效率高。
