一种基于LSTM神经网络建模的时域电磁正演方法
2021-06-28武风波范梦宁刘文远周远国
武风波,范梦宁,刘文远,赵 盼,周远国
(1.西安科技大学 通信与信息工程学院,陕西 西安 710054;2.陕西科技大学 电子信息与人工智能学院,陕西 西安 710021)
计算电磁仿真研究在学术和工程领域中应用十分广泛,如天线和电路设计、目标探测、地球物理勘探、纳米光学等许多相关领域[1]。传统的计算电磁方法有: 时域有限差分法(finite-difference time-domain, FDTD)[2-3]、有限元法(finite element method, FEM)[4]、谱元法[5]、时域积分方程法(time domain integral equation, TDIE)[6]、矩量法(method of moments, MOM)[7]等,这些方法都能准确地计算电磁问题。但由于上述方法都需要进行大规模的网格剖分,对于大的电磁正演模型将会占用大量的计算资源,需要大量的计算时间,且有的方法对于电磁正演模型的形状有限制。随着神经网络、人工智能的快速发展,神经网络建模方法在很多领域得到应用[8-10],大大提高了计算效率。神经网络具有学习复杂趋势的能力,并基于这一趋势能预测出新的或未来的信息,因此,研究人员利用该特点将神经网络应用于模拟复杂问题,如格林函数[11]、泊松方程[12]和流体力学[13]等。在这些工作中,神经网络从传统求解器模拟的数据中学习,得到经验模型,从而快速准确地预测结果,并且取得了较好的效果。而目前关于神经网络在电磁正演问题中的应用研究较少,FENG等搭建了一个基于卷积神经网络(convolutional neural networks, CNNs)的电磁正演模型,能够正确预测二维电磁辐射特性,但其泛化性不够强,且需要大量训练样本的支持,训练此神经网络模型耗时较长[14];ZHANG等搭建了循环神经网络(recurrent neural network, RNN)宏模型来进行微带低通滤波器的电磁仿真分析,速度与传统的电磁正演方法相比有了数倍提升,但是训练误差较大[15]。
针对上述问题本文考虑采用适合处理时间序列的长短时记忆(long short-term memory, LSTM)[16-18]神经网络模型来对电磁正演问题进行求解,提出了基于LSTM神经网络的电磁正演模型,以及适用于LSTM神经网络的电磁正演模型训练算法,并搭建了一个基于LSTM神经网络的近似模型。此方法仅需要少量的训练样本就能快速训练出基于LSTM神经网络的电磁正演模型,同时将该LSTM神经网络的预测结果与FDTD计算结果进行对比,在保证精度的情况下,单个样本的计算速度比FDTD方法提高了1 000多倍。初步的数值研究证明了该算法的可行性,成功实现了快速准确预测空间中电场分布的目的。
1 基于LSTM神经网络的电磁正演模型
LSTM神经网络模型通过 “门”来控制丢弃或保留信息,从而实现遗忘或记忆的功能。在本问题中,基于LSTM神经网络的电磁正演模型如图1所示。其基本结构由遗忘门、输入门和输出门3个门组成,这3个门相互作用从而控制LSTM神经网络最终的输出。LSTM神经网络的关键是单元状态,LSTM神经网络通过遗忘门、输入门和输出门保护和控制单元状态。
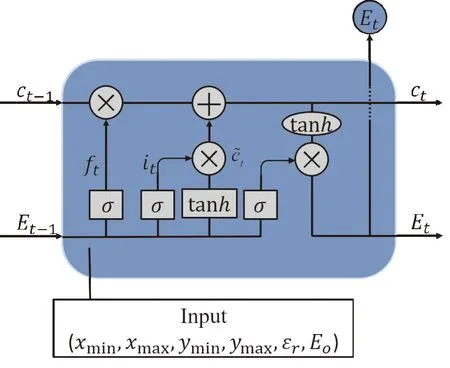
图1 LSTM结构图Fig.1 LSTM structure
遗忘门决定了哪些信息应该被保留或丢弃,在本问题中,遗忘门的输出被写为
ft=
σ(wf·[Et-1,xmin,xmax,ymin,ymax,εr,E0(t)]T+
bf)。
(1)
其中:σ(·)为sigmoid激活函数;xmin、xmax、ymin、ymax、εr、E0(t)为回归模型的输入;xmin、xmax、ymin、ymax为散射体的位置信息;εr为散射体的相对介电常数;E0(t)为t时刻对应的背景的电场值;ft为t时刻遗忘门的输出;Et-1为t-1时刻的输出电场;bf为遗忘门的偏置;wf为遗忘门的权值矩阵。
输入门决定了需要多少信息作为输入才能生成当前状态。计算公式为
it=
σ(wi·[Et-1,xmin,xmax,ymin,ymax,εr,E0(t)]T+bi)。
(2)
其中,wi和bi分别表示输入门的权值矩阵和偏置。可以看出,it与ft相似,两个门均由Et-1和xmin、xmax、ymin、ymax、εr、E0(t)共同确定。
LSTM神经网络通过添加遗忘门和输入门所控制的信息来确定当前时刻t的隐藏状态ct,长期信息由ft控制,短期信息由it控制,具体的计算公式为
tanh(wc·[Et-1,xmin,xmax,ymin,ymax,εr,E0(t)]T+
bc),
(3)
(4)
其中:tanh(·)为激活函数;wc和bc分别为电流门的权值矩阵和偏置。
LSTM神经网络的输出门控制最终有多少信息作为输出,输出门用ot表示,具体的计算公式为
ot=
σ(wo[Et-1,xmin,xmax,ymin,ymax,εr,E0(t)]T+bo)。
(5)
由于3个门相互作用,控制LSTM神经网络的输出,因此,LSTM电场Et的最终输出定义为
Et=ot*tan(ct)。
(6)
由以上LSTM神经网络的结构特点可知,LSTM神经网络非常适合处理与时间序列高度相关的问题,“门”结构能够有选择性的决定信息的保留。而时域电磁场的变化在时间上是相互关联的,电场值E的变化,不仅与散射体的位置信息和相对介电常数信息有关,与当前时刻的背景场有关,也与时间密切相关,这些特征之间对所求电场值E的影响关系,就可以靠“门”结构进行判断,最终预测出结果。因此,将LSTM神经网络模型引入时域电磁正演领域是可行的。
2 LSTM神经网络的电磁正演模型训练算法
将LSTM神经网络用于时域电磁正演不仅保证了计算精度,同时也加快了电磁计算的速度。为了建立LSTM神经网络的电磁正演模型,本文提出了一套算法,算法如下所述。图2为LSTM神经网络求解电磁正演的算法流程图。
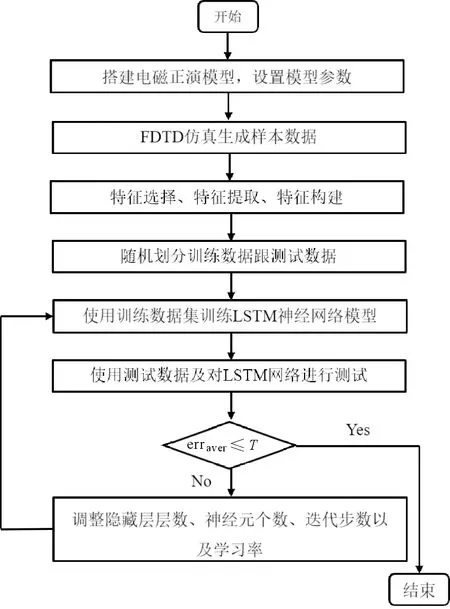
图2 算法流程图Fig.2 Algorithm flow chart
算法步骤如下:
1) 根据所要求解的电磁问题,建立电磁正演模型,得到所需要的样本数据。
2) 根据样本数据特征,确定LSTM神经网络为解决电磁正演的神经网络模型,以及LSTM神经网络的输入输出,并确定训练停止的阈值T。
3) 划分样本数据为训练集跟测试集两部分,选择合适的归一化标准对样本数据进行归一化处理,以便更快更好地训练出用于电磁正演的LSTM神经网络模型。
4) 选择合适的神经网络超参数以及迭代步数等,用训练集对LSTM神经网络模型进行训练。
5) 测试集对训练好的神经网络模型进行测试,验证网络的准确性与泛化性。
6) 通过对比LSTM神经网络预测结果与FDTD仿真结果的相对误差erraver来判断神经网络模型是否训练良好。
7) 若平均相对误差小于训练停止的阈值T,则表示网络训练良好,否则重新执行步骤4)。
通过该算法,一旦神经网络模型训练和测试成功,不仅可以快速对电磁正演问题进行求解,而且对类似问题均可以直接进行求解,传统FDTD方法对于不同问题则需要进行重新建模,本文提出的算法大大提高了计算效率。
3 LSTM神经网络的电磁正演模型搭建与算法验证
在本研究中,针对电磁散射问题,搭建了基于tensorflow框架的LSTM神经网络。使用Matlab正演程序生成样本数据集,并随机划分为训练数据集、测试数据集。将训练数据集输入到LSTM神经网络经过训练后, 用测试数据集验证该LSTM神经网络的性能。
3.1 电磁正演样本数据建模
本文电磁正演仿真建模如图3所示。电磁正演模型分为两层,上层背景介质的相对介电常数设置为1,电导率为0,下层背景介质的相对介电常数设置为2,电导率为0.000 1,散射体在下层区域。整个计算区域的大小为10 m×10 m,散射体遍历的预测区域的尺寸为7 m×7 m,被划分为70×70个单元,每个单元格的大小为Δx=Δy=0.1。有5个发射源,用黄色的点表示,一个接收点,用红色的点表示,它们都被放置在下层介质上方,发射源为高斯源,中心频率为0.15 GHz。
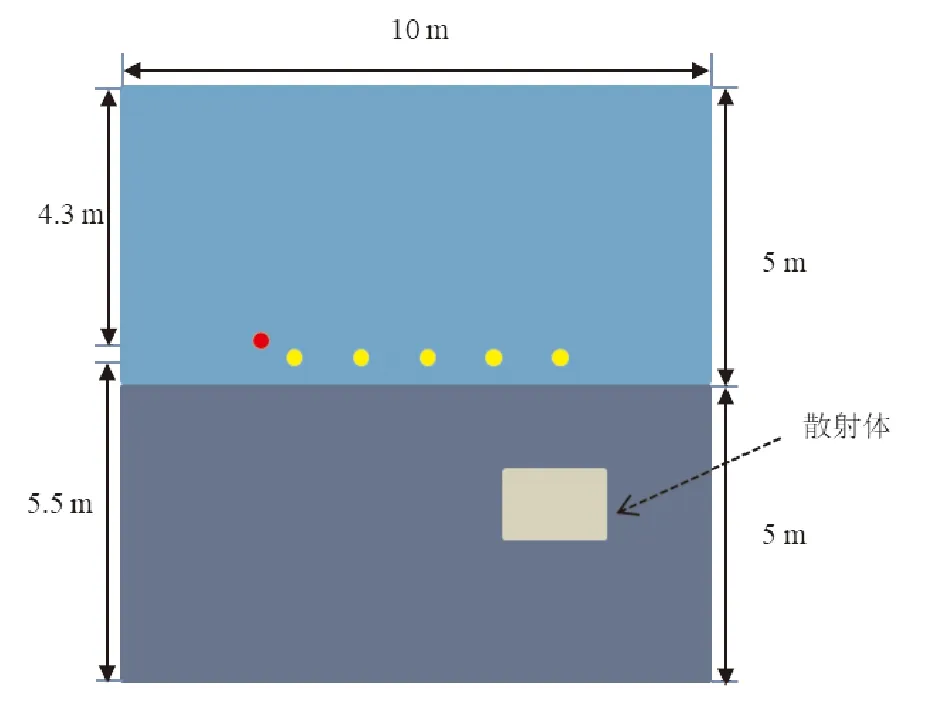
图3 二维电磁正演模型示意图Fig.3 2-D electromagnetic forward modeling
3.2 LSTM神经网络的电磁正演模型训练与预测
本文构造了40个均匀散射体,形状为长方体,它们为大小在[1 m×1 m,0.5 m×1 m,1 m×0.5 m,0.5 m×0.5 m,0.5 m×0.75 m,0.75 m×0.5 m,1 m×0.75 m,0.75 m×1 m]之中,相对介电常数在[3,4,5,6,7]之中的随机组合,电导率为0.001,位置在下层预测区域内随机变化。一共组成3 399组样本数据,用于训练的有154组,用于测试的有3 245组。对LSTM神经网络进行训练,花费1 h左右,训练3 000次后,训练的损失函数降低到10-4以下,如图4所示。
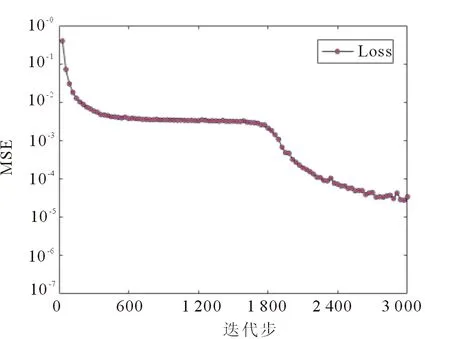
图4 训练损失函数Fig.4 Training loss curve
图5是从3 245组测试样本中随机抽取的两个样本的电磁散射结果。由图5可以看出基于LSTM神经网络的电磁正演模型预测的电场值与FDTD计算电场结果吻合地较好,这意味着经过3 000次训练的LSTM神经网络的电磁正演模型对于电磁正演是可靠的。

图5 LSTM预测二维电磁散射结果Fig.5 LSTM predicts results of 2-D electromagnetic scattering
3.3 电磁正演预测分析
为了更详细地比较LSTM神经网络预测的电场值和FDTD数值计算的电场值,使用LSTM神经网络模型中的平均相对误差erraver来衡量预测的准确性。其公式为
(7)
ELSTM(j)、EFDTD(j)分别为LSTM神经网络预测的电场值、FDTD数值计算的电场值,erraver为样本的平均相对误差。为了直观地看出预测样本的误差分布情况,绘制了平均相对误差分布散点图,如图6所示。可以看出,测试样本的erraver全都小于2%,结果表明基于LSTM神经网络的电磁正演模型具有非常高的准确性。

图6 平均相对误差分布Fig.6 Mean relative error distribution
同时为了对比本文提出的算法与传统FDTD在时间上的差异,验证了两者在相同计算机硬件环境下计算单一样本的时间开销,结果如表1所示。由表1可以看出在相同计算机硬件环境下基于LSTM神经网络的电磁正演模型求解电场在速度上大大优于FDTD方法,前者的计算速度是后者1 809倍。

表1 LSTM预测电场与FDTD数值计算时间对比
4 结语
本文提出了一种基于 LSTM神经网络的电磁正演模型,以及适用于LSTM神经网络的电磁正演模型训练算法。该方法利用LSTM神经网络的结构特点进行电磁正演建模,从而对时域电磁散射特性进行快速求解,与传统的FDTD方法相比,在保证精度的情况下,有效提高了时域电磁正演的求解速度。本文以二维时域电场问题为例进行验证,所提出方法的计算速度是传统的FDTD方法的上千倍。这项研究表明,利用LSTM神经网络的灵活性,可以建立一个提供实时响应的快速电磁求解器。
